摆动喷管与惯性器件超谐波耦合仿真研究

付 玮，孙 颖，王恩泽，段佳桐，戴婷婷

(1. 北京强度环境研究所，北京 100076；2. 北京宇航系统工程研究所，北京 100076)

0 引言

摆动喷管是推力矢量控制(TVC)的一种主要手段，广泛应用于各型飞行器中[1]。该控制方法通过改变喷出气流的方向来获得足够的俯仰/偏航控制力矩，能有效提高控制效率并减少推力损失。由于摆动喷管惯量较大，工作过程中容易激起飞行器结构的弹性振动，经惯性器件感知后进入控制系统，导致结构弹性与控制系统耦合，即伺服弹性问题，对飞行控制造成不利影响。

目前摆动喷管弹性耦合问题相关研究较少，主要是摆动喷管小系统的动态特性[2]以及谐振放大[3]相关研究，而伺服弹性研究重点集中在传感器布局[4]以及控制算法改进[5]，鲜有结构动力学方面相关研究。由于摆动喷管存在强非线性特征，可能造成伺服系统与惯性器件的耦合效应，对控制设计产生潜在的风险。因此，本文从结构动力学角度建立了全飞行器开环频率特性模型，对摆动喷管伺服系统非线性特征与惯性器件的耦合效应开展研究，用有限元方法模拟了超谐波共振耦合效应，并基于该模型讨论了解决该问题的技术途径，相关研究可为解决非线性耦合问题的设计与优化工作提供参考。

1 摆喷激励下的全飞行器开环频率特性模型

飞行器开环传递函数一般是指伺服指令输入到惯性器件输出的传递函数，是控制稳定性分析的重要依据，其原理框图见图1。其中r为伺服转角指令输入，δφ为摆动喷管转角，φgr为飞行器结构在惯性器件安装位置的转角，e为惯性器件角速率输出。从伺服转角指令输入到惯性器件输出共经历伺服系统传递特性、飞行器结构和惯性器件小系统这3个环节。

利用各环节的传递函数可以得到开环传递特性的表达式

(1)

式中，Gs，Gd，Gg分别代表伺服系统、飞行器结构和惯性器件系统的传递函数。本文从结构动力学角度建立开环传递特性模型(见图2)，并开展仿真研究。

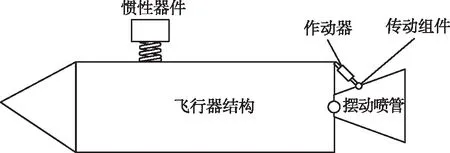
图2 全飞行器结构动力学模型示意图Fig.2 Schematic diagram of the dynamic model of the whole aircraft structure

1.1 飞行器结构各环节建模方法

飞行器结构可以认为是线性系统，在小扰动理论下进行运动方程的线性化[6]，忽略气动力的影响，有以下简化的运动方程组

(2)

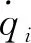
(3)

惯性器件安装位置可能存在局部刚度较弱的情况，用弹簧-质量模型模拟角传递特性环节，参考文献[8]的研究方法建立动力学微分方程组

(4)

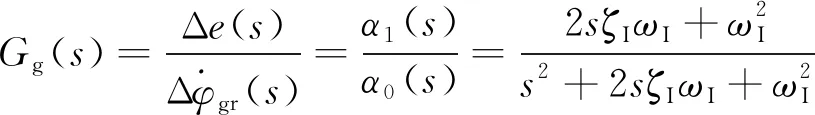
(5)

伺服控制驱动器、作动器、传动组件与摆动喷管负载共同组成了伺服系统，飞控系统通过向伺服系统发送指令信号，控制摆动喷管完成不同转角动作。

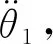
(6)

传动组件具有非线性特征，K1和c1往往具有非线性特征，分别是转角和角速度的函数。由于伺服作动器自身的控制回路有滤波器或陷波器，对指令信号r(t)有调幅的效果，此处引入参数A(t)实现该环节的模拟，基于卷积定理有

θ0(t)=A(t)*r(t)

(7)

图3 伺服系统等效结构动力学模型Fig.3 Equivalent structural dynamic model of servo system

为了获得伺服系统传递函数，将式(7)代入微分方程组(6)求解，工程上一般通过等效线性化方法[9]得到等效刚度Keq与等效阻尼ceq，进而得到传递函数

(8)

通过式(3)(5)(8)可以获得从伺服角度指令输入到惯性器件角速度输出的开环传递函数。

等效线性化方法适用于主共振的研究，对非线性系统的超谐波共振，只能在时域开展研究工作，由于非线性刚度阻尼的存在，求解微分方程非常困难，只能采用数值解法或半解析方法求解。

1.2 飞行器结构有限元分析方法

有限元非线性瞬态响应计算方法是开展非线性系统时域研究的有效手段。结合1.1节中的全系统结构动力学模型，用有限元方法建模计算，是高效可靠的方法。

飞行器结构采用梁单元建模，整个飞行器由50个梁单元组成，单元编号1～50。为了模拟真实飞行工况，采用“自由-自由”边界，即对全飞行器结构不施加任何边界。

伺服系统有限元模型示意图见图4，图中黑色代表结构单元，玫红色代表多点约束(Multi-Point Constraints，MPC)单元。摆动喷管负载只考虑惯量效应，用梁单元建模，单元编号为51和52，摆动喷管与飞行器之间用MPC单元模拟球窝连接，编号为1，约束平动自由度，放开转动自由度。

图4 伺服系统有限元建模方法Fig.4 Finite element modeling method for servo system

考虑作动器位移激励的工作过程，采用有限元在基础激励分析中常用的大刚度法，用大刚度弹簧单元57模拟作动器，用弹簧阻尼单元58模拟具有非线性特征的传动组件，单元57一端利用编号为2的MPC固连在飞行器结构上，另一端与单元58连接。同时对单元57两端施加同值反向动态力F(t)，根据大刚度假设，K0>>K1，可以认为θ0为作动器的位移反馈，此时

θ0(t)≈F(t)/K0/L1

(9)

其中，L1为摆喷转轴到动态力F(t)作用线之间的距离。根据式(7)与式(9)可得到满足θ0(t)条件的F(t)表达式

F(t)=A(t)*r(t)·K0·L1

(10)

由于造成伺服系统的非线性因素很多，而传动组件间隙是伺服系统的主要结构特征，造成了该环节刚度非线性，本文仅考虑间隙非线性的影响。含间隙系统弹性恢复力表达式如下

(11)

其中，单边间隙绝对值为d，间隙外刚度为k，间隙内刚度为ak。

惯性器件小系统建模依据1.1节的方法，采用弹簧-质量模型，见图5。在飞行器结构某位置建立弹簧阻尼单元55模拟飞行器在惯性器件安装位置的局部刚度，建立集中质量单元56，模拟惯性器件的惯量。

图5 惯性器件小系统有限元建模方法Fig.5 Finite element modeling method for inertial device system

为了验证摆动喷管与惯性器件超谐波耦合效应，整个有限元模型参数设计原则为飞行器前几阶模态频率不能与惯性器件小系统以及摆动喷管小系统谐振频率一致。

2 伺服系统超谐波共振的耦合效应分析

2.1 线性系统开环传递特性分析

对于线性系统，只需令式(11)中a=1即可，此处设定k=10 000，开展有限元仿真计算。

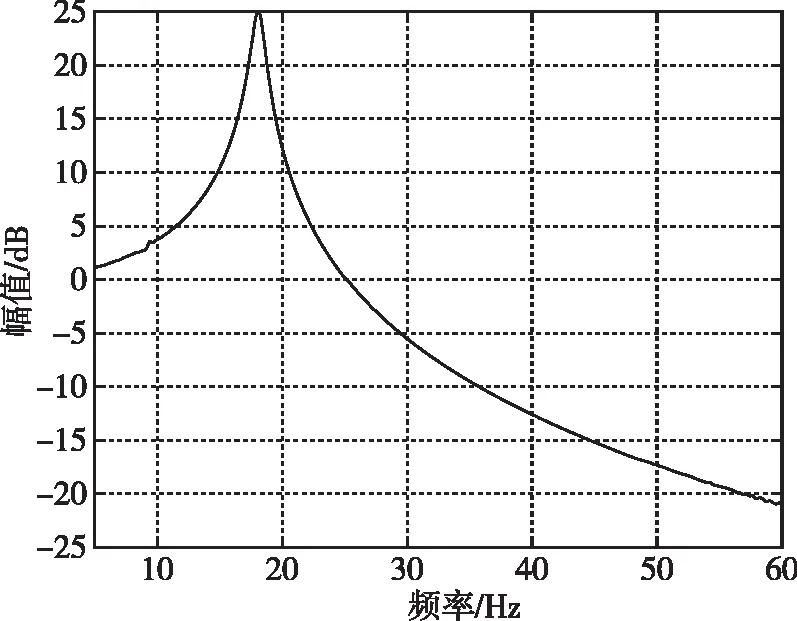
俯仰方向前3阶模态频率与振型见表1，30 Hz以内有两阶模态。本文模拟开环传递特性的试验获取方法，向伺服系统发送连续正弦扫频指令，测量作动器反馈、摆动喷管、惯性器件安装位置以及惯性器件本体环节的俯仰通道响应。此处将伺服系统的滤波环节增益置1，即反馈环节与指令一致。线性系统开环传递特性幅频曲线见图6，其中图6(a)为伺服系统传递特性，谐振频率为18.1 Hz，在前两阶模态频率之间；图6(b)为惯性器件角速度响应对角度指令的开环传递特性，图中前3阶模态频率在开环特性曲线中都有明显响应，伺服系统的谐振频率也有明显的呈现，惯性器件局部频率约53.6 Hz，已经超过第3阶模态频率。在该算例中，伺服系统谐振频率避开了飞行器模态，而惯性器件局部频率较高，最大限度避免了结构耦合效应，30 Hz以内惯性器件与安装位置响应基本一致。

表1 俯仰方向前3阶模态频率与振型

(a)伺服系统传递特性

(b)惯性器件开环传递特性图6 线性系统开环传递特性幅频曲线Fig.6 Open-loop transfer function magnitude-frequency curves of linear system

2.2 非线性系统开环传递特性结构耦合分析

令式(11)中k=10 000，a=0.01，d=0.015，间隙外刚度k与线性系统保持一致，求解含间隙系统的各环节非线性瞬态响应，进而获得这些环节的传递特性。开环传递特性幅频曲线见图7，分别为伺服系统和惯性器件的传递特性，对比线性系统，有间隙时伺服系统传递特性曲线有明显畸变，惯性器件的特性曲线中同样可以反映出飞行器模态、伺服系统特性以及惯性器件局部特性，只是谐振峰放大倍数略有差别。

(b)惯性器件开环传递特性图7 非线性系统开环传递特性幅频曲线Fig.7 Open-loop transfer function magnitude-frequency curves of the nonlinear system

对比无间隙和有间隙状态下各环节时域响应，摆动喷管响应见图8。 图8(a)为谐振峰位置附近的时域响应曲线，有间隙状态下时域曲线的包络在谐振峰位置发生明显畸变，从时频图8(b)中可以发现，有间隙状态下响应叠加了3倍频的分量。惯性器件本体响应见图9。图9(a)为角速度响应时域曲线，圆圈标记处是明显的谐振放大，通过时频图9(b)可知，该位置响应不是二阶弹性振动频率25.4 Hz，也不是伺服系统的谐振频率17.6 Hz，而是惯性器件局部频率53.6 Hz，此时扫频指令的频率仅为18.3 Hz，相较无间隙状态，该处出现了明显的超谐波共振现象，即伺服系统主共振频率的3倍频与惯性器件局部弹性频率发生耦合，造成后者输出响应异常放大。

(a)时域曲线

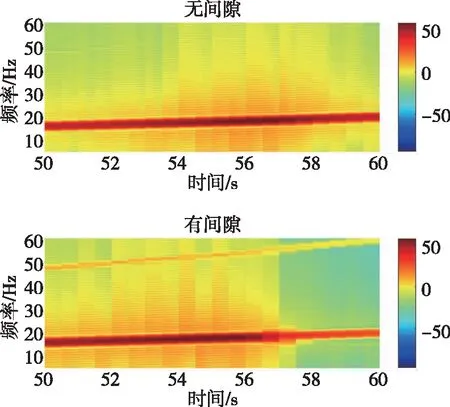
(b)时频图图8 摆动喷管转角响应Fig.8 Angular response of the swing nozzle

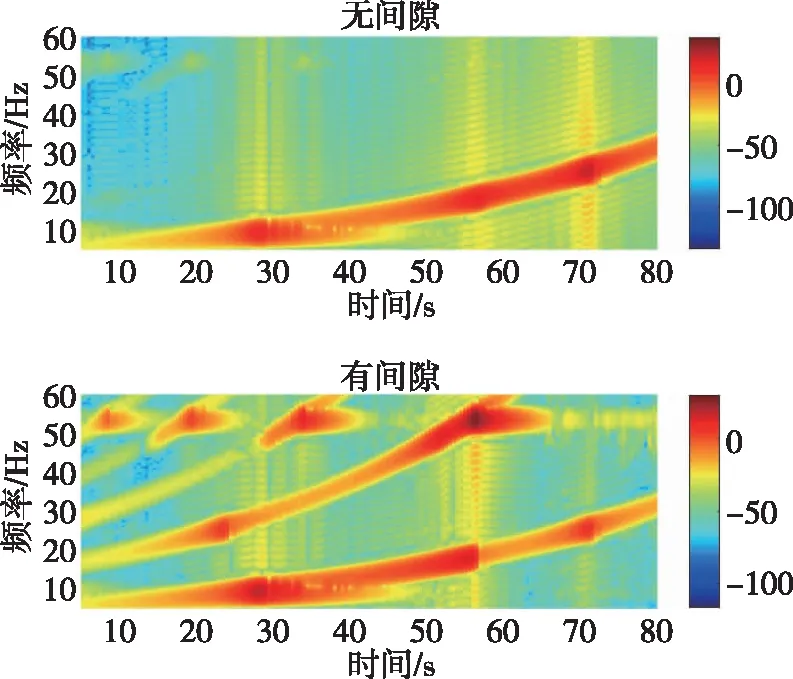
(b)时频图图9 惯性器件角速度响应Fig.9 Angular velocity response of the inertial device

由于在设计阶段，无法建立伺服系统准确的非线性模型，需要在开环伺服弹性试验中开展相关验证工作，以发现摆动喷管与惯性器件的超谐波共振耦合的隐患。

3 超谐波共振耦合问题解决方案讨论

从以上算例结果可知，伺服系统的结构非线性特征容易导致摆动喷管响应出现倍频分量，虽然该分量与基频相比能量很小，但如果与惯性器件局部弹性频率发生耦合，就会在低频指令下产生明显的超谐波谐振放大现象，对控制系统造成安全隐患。

该耦合问题主要由伺服系统非线性特征与惯性器件的局部弹性特征造成，最有效的解决的方法是避免二者出现接近的谐振频率。由于惯性器件局部弹性频率明显高于伺服系统的谐振频率，为避免谐振耦合，只能继续提高其局部频率，而伺服系统的强非线性特性产生了超谐波频率分量，降低其谐波共振也能减小耦合效应，因此解决该问题可以从以下几种途径开展工作：提高惯性器件局部弹性频率、减小传动组件间隙以及在伺服作动器控制回路增加滤波器，对作动器反馈信号进行幅值调制。下面利用2.2节中的算例分别对这几种途径的可行性进行讨论。

3.1 提高惯性器件局部弹性频率

为了避免伺服系统倍频与惯性器件局部谐振频率的耦合现象，可以通过提高惯性器件局部谐振频率的方法避开低阶倍频耦合，即提高方程组(4)中的ωI。图10是惯性器件局部刚度提高1倍后角速度响应，从图10(a)中可见时域曲线的幅值水平显著降低，从图10(b)中可见摆动喷管谐振频率附近倍频位置没有能量集中的现象。该方法能够有效降低惯性器件耦合放大的倍数，但实施过程涉及结构改进，在研制末期实现比较困难。

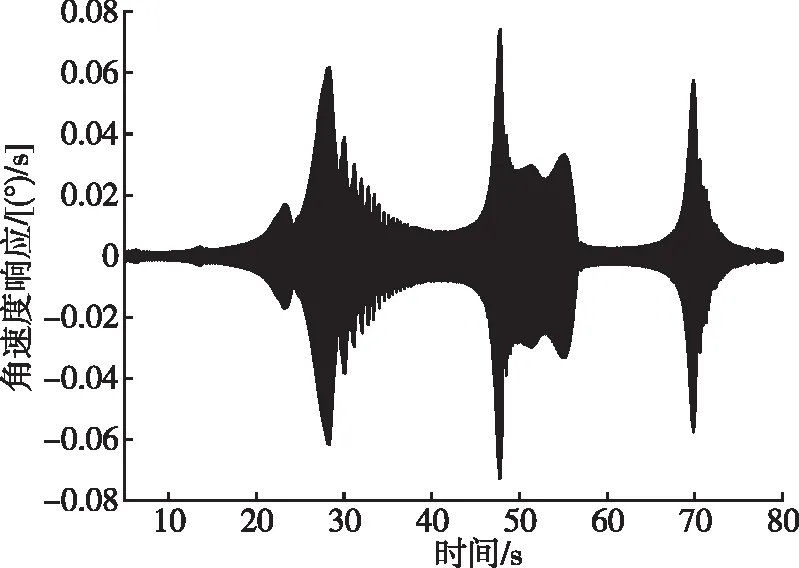
(a)时域曲线

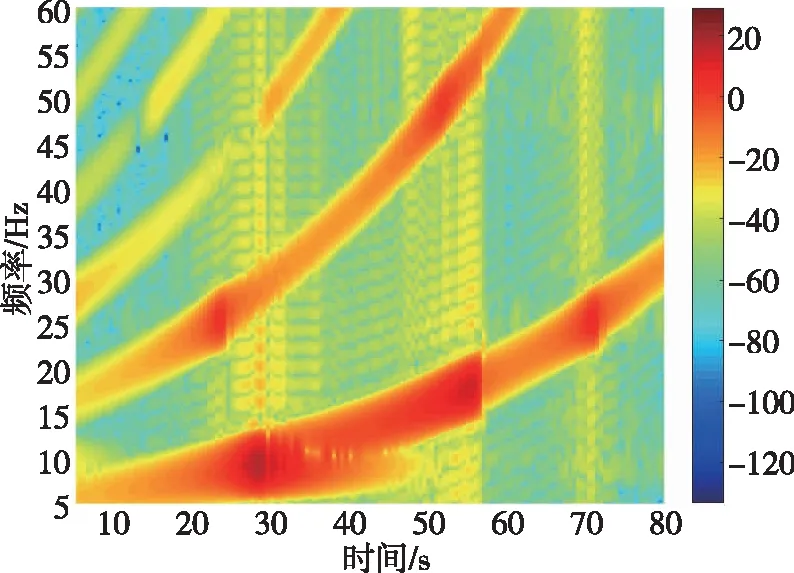
(b)时频图图10 改进结构后惯性器件角速度响应Fig10 Angular velocity response of the inertial device after improve the structure

3.2 减小传动组件间隙

通过减小间隙可以降低系统非线性特征，以减小摆动喷管运动时产生的倍频分量，操作方法为减小式(11)中间隙绝对值d。不同间隙下摆动喷管谐振频率附近惯性器件最大响应幅值见表2，表中可见，减小间隙可以有效改善超谐波共振耦合现象，但该方法的实施需要大幅提高装配工艺，对成本和研制周期而言并不经济。

表2 不同间隙下摆动喷管谐振频率附近惯性器件最大响应幅值

3.3 在伺服作动器控制回路增加滤波器

通过修改伺服控制器控制算法，实现对作动器反馈信号进行幅值调制，降低伺服系统谐振峰的幅值，抑制摆动喷管响应的倍频分量，可以降低耦合效应。仿真算法为利用式(7)对指令信号滤波，得到等效的作动器反馈信号，该反馈信号与摆动喷管响应信号对指令的传递函数见图11，摆动喷管幅频曲线在谐振频率处被下拉6 dB。惯性器件的角速度响应见图12，其中图12(a)中可见，原超谐波共振耦合区域的响应已未见明显放大，图12(b)中可见惯性器件响应信号中已几乎没有倍频分量。该方法改善超谐波共振效果明显，且只需要修改软件，通过上传的方式更新伺服控制器软件，就能实现耦合效应的抑制，适用于整个研制阶段。

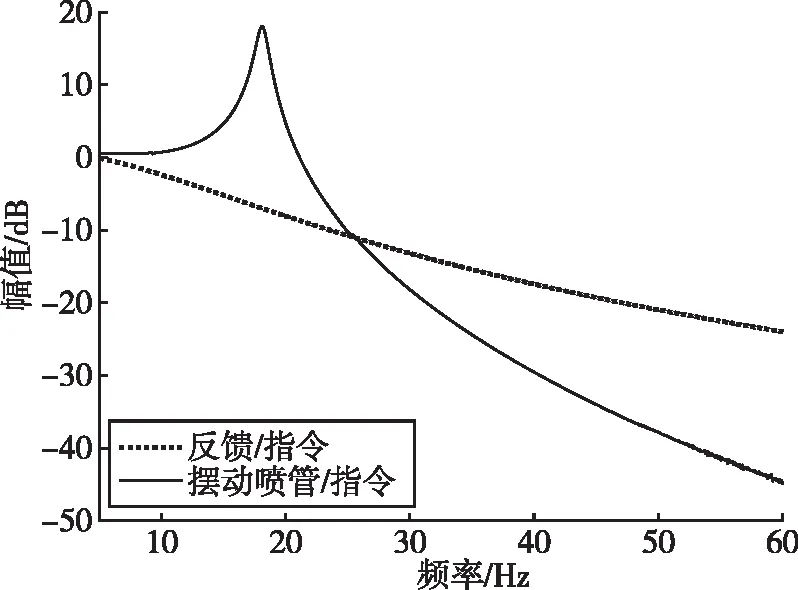
图11 伺服系统增加滤波器后反馈与摆动喷管传递特性Fig 11 Adding a filter to the servo system affects the transfer function between feedback and swing nozzle

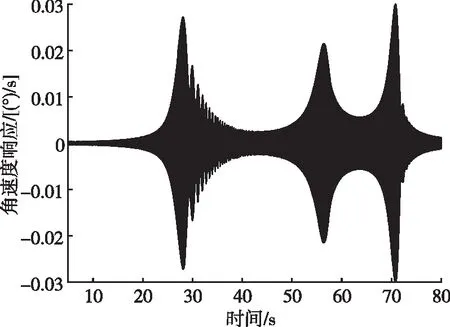
(a)时域曲线

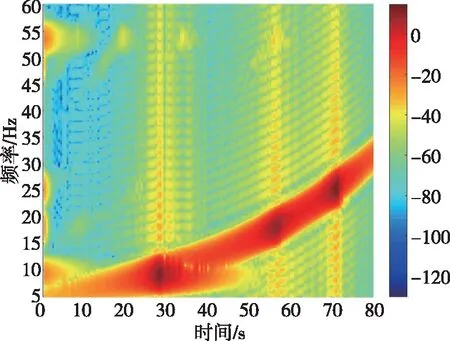
(b)时频图图12 伺服系统增加滤波器后惯性器件角速度响应Fig 12 The addition of a filter to the servo system affects the angular velocity response of the inertial device

4 结论

在考虑摆动喷管结构非线性特征的前提下建立了简化的飞行器全系统结构动力学模型，利用有限元方法对伺服系统超谐波共振的耦合效应进行了仿真分析，结论如下：

1)摆动喷管的间隙非线性存在与惯性器件的超谐波共振耦合效应的风险。

在产品设计时，无法准确地获取摆动喷管伺服系统的非线性模型，因此无法直接评估结构非线性耦合效应的影响，因此需要在全实物试验设计时考虑该影响因素。在开环伺服弹性试验中，也要关注超谐波共振现象与惯性器件的耦合效应。

2)通过滤波对作动器反馈信号调幅是解决超谐波耦合效应的有效手段。

通过加强惯性器件安装位置刚度以及减小伺服系统传动组件的装配间隙可以有效降低超谐波耦合效应的影响，但周期和成本并不合适，而对反馈信号滤波只需根据试验测得的数据修改伺服控制器软件，高效且成本较低。

型号设计中虽然会考虑结构耦合对控制系统的影响，但由于结构的强非线性因素，其超谐波或亚谐波现象所造成的耦合风险仍然很难在设计阶段予以排除，因此开展全实物伺服弹性试验是必要的。同时，继续开展伺服机构非线性建模与仿真研究也不可或缺，其研究成果可以作为控制设计的重要参考。