基于出行效用无差异阈值的组合交通客流分配模型

2023-12-12于晓桦刘欣萍毕亚茹田雨晗

交通运输工程与信息学报 2023年4期

于晓桦，刘欣萍，毕亚茹，田雨晗

（山东建筑大学，交通工程学院，济南 250101）

0 引言

随着城市化进程的加速，轨道交通出行方式逐渐在城市出行中占有主导地位。然而，由于城市轨道建设投资巨大，轨道交通往往无法在城市出行中提供“门到门”的服务。为了扩大轨道交通服务范围，让更多人从中受益，需要轨道交通与其他交通方式进行衔接，形成组合交通方式[1]。如何鼓励与推广组合交通方式，特别是当私人交通方式的出行效用高于组合交通效用时，如何提升组合交通的吸引力，成为一个重要课题领域。

组合交通出行方式的研究主要集中在出行选择行为和组合交通流量分配方面。Fernandez 等[2]最早考虑小汽车和地铁两种交通方式的组合出行行为，研究出行者对路径、交通方式和换乘点的选择问题，建立了固定需求均衡分配模型。在此基础上，许多学者进行了进一步的深化研究，如Lam等[3]研究了小汽车出行与小汽车换乘地铁两种交通方式，建立了弹性需求下的多模式交通网络均衡模型；Fan 等[4]构建了单一出行和停车换乘组合出行的多模式城市交通网络，提出了一个综合了组合方式划分与交通分配的通用不动点模型；张雪妍等[5]基于随机效用理论，分析了网络随机用户均衡条件，建立了考虑交通网络不确定性的组合出行交通分配模型；刘梦琪等[6]研究了在轨道交通与常规公交组合的交通方式下，不同收入人群的出行路径选择问题。

以往对交通分配问题的研究更多基于效用最大化原则[7-9]，但其中对于出行者以及出行行为的假设过于理想化。Simon[10]的有限理性决策理论认为，在实际决策中，人们通常无法获得所有备选方案的信息，也很难准确预测每个备选方案的后果，因此最终的选择往往是满意结果而不是最优结果。在此基础上，Coombs 等[11]提出了感知阈值的概念，即当变化低于某一阈值时，个体将感知不到差异[12-13]。这一概念逐渐演变为无差异阈值，并在交通领域得到广泛运用。Zheng 等[14]和Pan 等[15]分别在交通流特性实验和公交服务选择行为中引入了无差异阈值的概念，并证实了无差异阈值的存在。研究发现，如果不考虑无差异阈值，可能会导致估计和预测错误。这一结果表明无差异阈值会使传统的效用最大化理论在出行行为方面应用失效，增加了组合交通方式出行预测的不确定性。Wang 等[16]在研究公交服务的运营策略时发现，用户切换至新模式的决策过程并非简单的效用比较，而是当新模式的效用超过当前模式的效用加上一个阈值时才会发生切换；Jang 等[17]在后悔-喜悦选择模型中引入了容忍带和无差异带，发现当出行目的与工作相关时，对属性差异的容忍度较低，而与工作无关时，对属性差异的敏感度较低；Long 等[18]分析了不同信息模式下，出行者路径选择的转换阈值。显然无差异阈值的概念已被广泛接受，国内一些学者还将效用无差异阈值应用于出行者的出行方式选择和出行路径选择行为分析中，构建了相应的出行行为决策模型[19-20]。

目前，在对组合交通的研究中大都忽略了出行者的非完全理性行为。本文构建了一种基于出行效用无差异阈值的组合交通客流分配模型，将组合交通出行的选择决策过程用多级网络模型来表示[21-22]，包括小汽车道路网络、在换乘点展开的平面拓展网络以及出行方式网络。本研究在建立组合交通方式多级网络模型的基础上，考虑出行者在选择环节能感知到的效用无差异阈值，探索无差异阈值对组合交通方式客流分担的影响及其转移演化机理。

1 组合交通出行选择行为分析

组合交通方式是由各个单一交通方式通过换乘衔接而形成的出行方式，但并非所有组合都现实可行。考虑到轨道交通在公共交通网络中的骨干作用，仅考虑非步行交通方式与轨道交通衔接的组合交通方式。组合交通方式的选择实际上是非轨道交通站点区域的出行者对轨道交通方式的选择，其出行过程描述如图1所示。

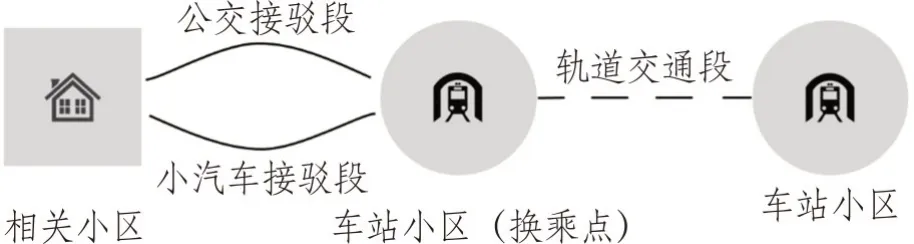
图1 组合交通的出行过程Fig.1 Travel process of combined transportation

与单一交通方式出行不同，如果出行者在决策过程中选择了组合交通方式，则同时面临着对换乘站点的选择和对线路的选择。如图2所示，当出行者选择轨道交通组合出行时，可以选择在S1和S2换乘（图（a）），出行者会权衡路径效用和换乘效用，综合考虑进行选择（图（b））。因此，交通出行行为选择可以分为三个层次，首先是对出行方式的选择，包括轨道出行（组合出行）和小汽车出行；其次是组合出行对换乘点的选择；最后是对公共交通路线或小汽车路径的选择。三个层次选择的关联性在于下一层的选择肢效用影响上一层选择的综合效用。

图2 轨道交通组合出行间的选择对比示意图Fig.2 Comparative illustration of the choice between combined travel modes in rail transit.

在多级决策过程中，假设每一层级的出行效用由固定部分（Vi）和随机部分（εi）构成，即Ui=Vi+εi，其中随机部分相互独立且服从Gumble 分布，则客流分配模型可以用Nested Logit 模型形式表示。其出行选择的概率可以表示为“选择哪种交通方式、在哪个换乘点换乘、选择哪条具体路径”的概率[22]，并表达为条件概率形式：式中：Ρmhk表示多级网络中选择交通方式m，在换乘点h处换乘并选择道路路径k的概率；Ρm表示选择交通方式m的概率（包括单一交通方式和组合交通方式）；Ρh|m表示选择交通方式m并选择换乘点h的概率；Ρk|mh表示选择交通方式m与换乘点h的前提下，选择道路路径k的概率。

2 模型建立

2.1 基于无差异阈值的选择肢效用分析

为考虑出行者的非完全理性行为，将无差异阈值引入到Nested Logit 模型中。当不同选择肢的效用差绝对值小于出行者能够感知的无差异阈值时，出行者将无法区分这两种选择肢的效用大小，而基于个人偏好或随机做出选择；反之，出行者将依据效用最大化原则作出选择，如下式所示[19]（其中定义出行效用为负效用，用出行阻抗表示）：

式中：p1为出行者选择方案1 的可能性；U1和U2分别为方案1 和方案2 的出行阻抗；τ1为出行者对两种方案的偏好系数，0 ≤τ1≤1；Δ1为出行者在方案1 与方案2 之间能感知到的无差异阈值，且假设所有出行者对于相同的选择肢具有相同的无差异阈值，Δ1≥0。

当方案1 与方案2 的出行阻抗差大于Δ1（小于-Δ1）时，出行者能够区分这两种方案的效用大小，可以做出理性决策，即绝对会选择方案2（方案1）；当方案1与方案2的出行阻抗差大于-Δ1且小于Δ1时，出行者将根据个人偏好τ1或进行随机选择，若τ1=0.5，则表示出行者对两方案没有偏好，做出的选择是完全随机的；τ1越接近1 说明出行者对方案1 的偏好越强烈，越接近0 说明对方案2 的偏好越强烈。

2.2 基于多级网络的出行效用分析

组合交通出行的决策过程分为三级选择，包括方式选择级、换乘点选择级以及路径选择级，如图3所示。在多级网络中，将上层感知的出行效用无差异阈值作为合理的约束指标，用于指导下层的选择决策，从而建立基于无差异阈值的组合交通客流分配模型。而模型下层的出行效用影响上层选择的综合效用，每个层级的选择考虑的因素不同而生成多级效用。

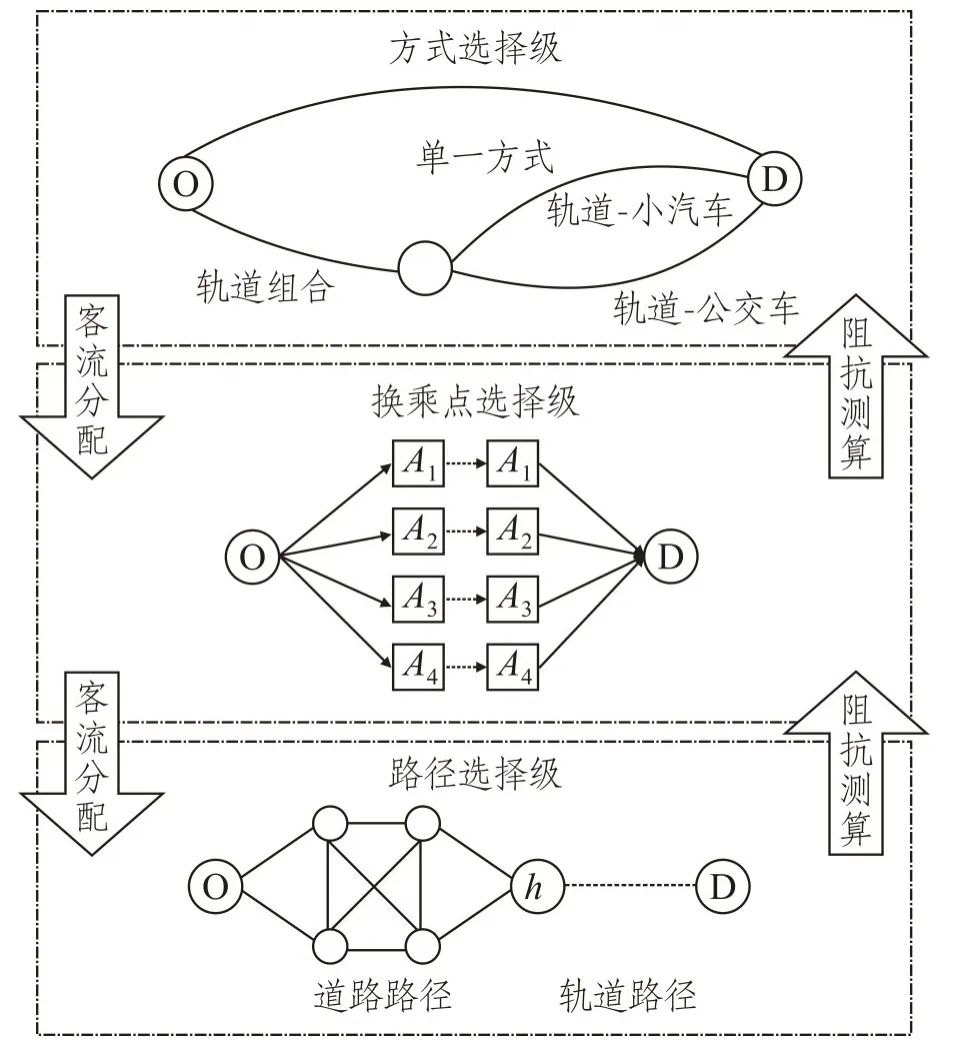
图3 多级网络层级划分示意图Fig.3 Illustration of hierarchical division in a multi-level network

因此从模型的第三级开始分别给出每一层级的客观出行阻抗，即出行效用的固定项。其中出行阻抗包括出行费用阻抗和出行时间阻抗。出行时间阻抗根据出行过程分为车内阻抗、等待阻抗、接驳阻抗和换乘阻抗。

（1）模型第三级——道路路径选择级

道路路径选择级中出行阻抗用接驳阻抗及费用表示。出行费用主要包括乘坐地铁和公交车的票价以及小汽车出行相关的燃油费用、车辆损耗费用等。接驳阻抗是指从一个交通方式（如公交车、小汽车等）到达轨道交通站点所需的时间阻抗。在道路路段的选择中，由于公共交通是确定的，接驳阻抗只涉及到实际交通网络中小汽车出行路段的选择，受自由流时间、路段流量与通行能力的影响。通常，接驳阻抗用BPR 函数表示为：

道路路径阻抗为：

式中：γ为时间成本参数；若路段j在路径k上时，=1，否则为0；π为路径费用。

（2）模型第二级——换乘点选择级

换乘点的选择问题仅存在于组合交通方式中。换乘阻抗用于表示从上一个交通方式到达轨道交通站点并完成换乘所花费的时间，受换乘距离和乘客步行速度的影响，可以表示为：

式中：L′为换乘站两站台之间的距离；νh为换乘乘客的步行速度，取5.4 km/h[23]。

换乘点阻抗为：

式中：V*sum(Vk)为路径的合成阻抗。

合成阻抗表达式如下所示：

其中：若换乘点h在路径k上，则=1，否则为0。

（3）模型第一级——交通方式选择级

交通方式选择级中出行阻抗包括车内阻抗和等待阻抗。

①车内阻抗表示乘客在车内的感知时间，由公共交通方式的运行时间和由于拥挤而产生的额外时间两部分组成，受发车频率、车辆运行时间、车内座位数、最大载客量以及人流量的影响，可以用公式表示为：

式中：ta为线路a上的车辆运行时间；Ya为车内拥挤而造成的额外成本参数[24]，如下式所示：

其中：xa为线路a的人流量；f为车辆发车频率；nseat为车内座位数；ca为最大载客量。A、Β为参数且A=1,Β=2。

②等待阻抗，表示乘客在站台的等待时间，与公共交通的发车频率、乘客到达分布有关。发车频率越高则乘客等待时间越少，因此认为乘客等待时间与发车频率成反比，即：

式中：λ=1，表示均匀随机的乘客到达分布与稳定的列车频率。

交通方式阻抗为：

式中：若交通方式m在路径k上时，则=1，否则为0；(Vh)为换乘点的合成阻抗，表达式如下所示：

式中：若交通方式m中存在换乘点h，则=1，否则为0。

在出行决策过程中将问题分解为三个层次，每个层次考虑不同的因素，以综合考虑多个因素对决策的影响而生成方式选择、换乘点选择和路径选择的多级效用。组合交通出行两点之间的多级效用可以用出行阻抗表示，即式（4）、式（6）、式（11）。

2.3 基于出行效用无差异阈值的Nested Logit模型

以方式选择为例，当两种方式的效用差在一定阈值间，出行者不一定会选择效用最大的方案。假设随机项服从(0,θm)的Gumble 分布，则由式（2）得基于无差异阈值的方式概率选择模型如下：

式中：Δm表示交通方式选择级的无差异阈值，体现出行者对于不同交通方式出行效用差的感知能力。同理，基于无差异阈值的换乘点概率选择模型和路径选择模型分别如式（14）、式（15）所示：

将式（13）～（15）带入式（1）即可得到具体到交通方式、换乘点及路径的出行概率。

上述模型得到的是只有两种方案可供选择时选择方案1 的概率，可将其拓展到有r（r≥3）种方案。此时，如果计算选择方案1的概率可遵循如下步骤：

（1）当方案1与其他方案的效用差均大于Δ时：

（2）当方案1与某一个方案的效用差小于Δ时：

（3）当方案1与某两个方案的效用差小于Δ时：

（4）当方案1与其他方案的效用差均小于Δ时：

因此，将选择概率分为r个部分，分别计算条件概率并相加，从而得到出行者选择方案1 的概率，表示如下：

3 模型求解

3.1 模型假设

（1）多级网络决策假设：选择出行方案时，出行者会进行多重考虑。特别是在组合交通出行中，出行者会先选择出行方式，再考虑换乘地点，最后选择合理的路径到达站点。出行者做出选择的前提是基于对出行方案的整体判断，例如选择组合交通方式时，出行者会考虑到达站点的便利性以及车站内的布局等因素。因此，在多级网络中，下一级选择的效用综合值会影响上一级的决策。

（2）无差异阈值假设：尽管出行者都希望选择出行效用最大的出行方案，但由于出行者对出行效用的感知与认识存在差异，无法准确判断出行效用真实值。因此，当两种出行方案的效用差异小于出行者能够感知到的无差异阈值时，出行者无法在两种选择方案中做出确定的选择，将根据偏好或者随机选择；反之，出行者会选择效用最大的出行方案。

（3）影响因素假设：出行者在制定出行方案时，会考虑各种影响因素，例如时间、费用、舒适性、换乘便利性等。在决策过程中，路径选择级主要考虑接驳效用与路径费用，而对于小汽车出行，则直接使用路径效用表示；在换乘点选择中，主要考虑换乘效用，包括换乘时间等因素，而在方式选择中，会考虑各种方式的出行时间与舒适性等因素。

3.2 模型算法

考虑无差异阈值下的Nested Logit 多级网络流量分配问题，采用连续平均算法（MSA），其具体算法步骤如下：

第1 步初始化。设置初始迭代次数n=0，迭代终止误差κ=0.001。在多级网络中计算各级网络效用与选择概率，根据总流量q计算所有被利用的路径上的初始流量值，即fmhk=Ρmhkq从而得到多级网络中各路段的初始流量，记为

第2 步更新效用。首先根据式（3）、式（4）更新模型第三级——道路路径选择的效用；再根据式（4）～（7）更新模型第二级——换乘点选择的效用；最后根据式（7）～（12）更新上级网络（交通方式选择）的效用。

第3步确定搜索路径。计算各层级网络下考虑无差异阈值的出行概率，再更新fmhk的流量，得到多级网络中路段的附加交通量，进而确定搜索方向为

第4步更新网络各路段流量：

第5步收敛性检验。如果该循环的收敛性满足收敛条件，则停止迭代并得出结果；否则返回第2步，n=n+1。将收敛条件定义为：

4 算例分析

设想一个交通网络如图4所示，用于模拟考虑出行效用无差异阈值条件下的组合交通客流分配问题。在此网络中，O 表示起点，D 表示终点，A 和B 表示换乘点；有小汽车出行路段OA、AD、OD、OB；轨道出行路段AD、BD；公交出行路段OB。每天有1 000 位出行者从O 点出发到达D 点，其中有3 种交通方式可供选择，分别是小汽车出行、小汽车+轨道出行、公交+轨道出行。建立出行行为选择树形结构如图5所示。

图4 交通网络算例Fig.4 Traffic network example

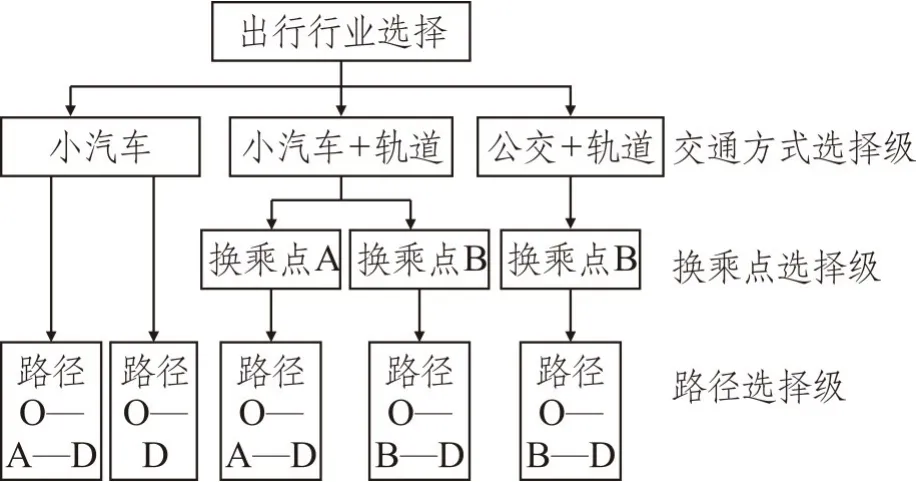
图5 交通出行行为选择树形结构图Fig.5 Tree diagram of transportation mode choice behavior

交通网络中的各项参数取值见表1、表2，出行链阻抗参数见表3。

表1 路径参数Tab.1 Parameters of the path

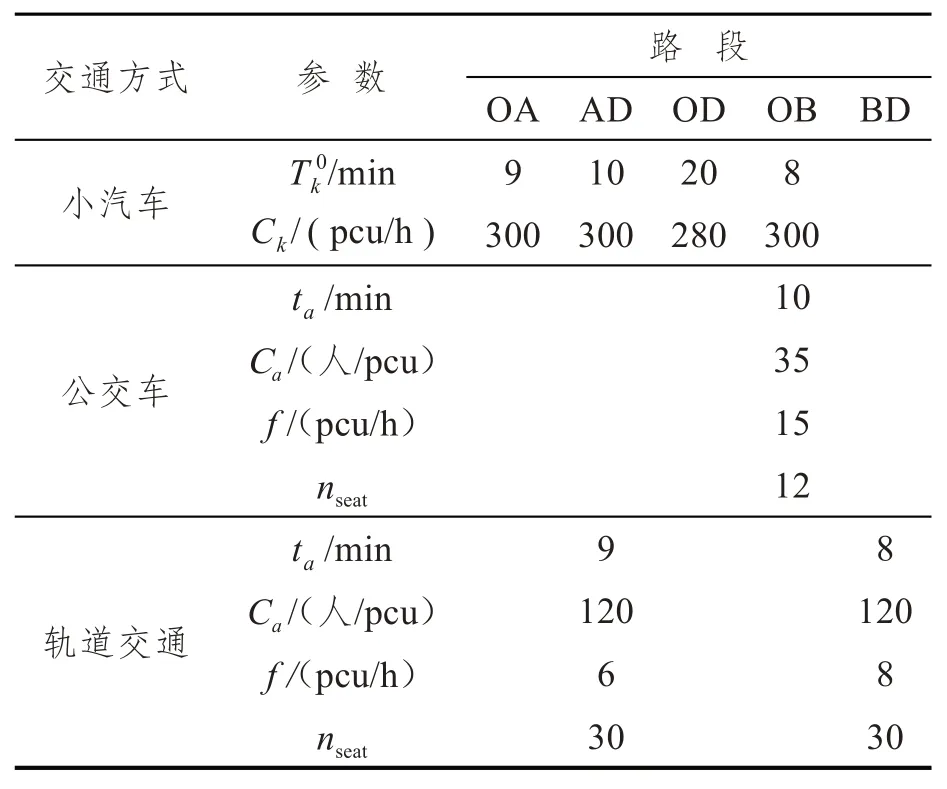
表2 路段参数Tab.2 Parameters of the link

表3 出行链阻抗参数Tab.3 Impedance parameters of the travel chain

选取a、b两种情况做流量分配结果的对比，情形a 中，不考虑无差异阈值，即假设出行者都会选择效用最大的方案；情形b 中，假设出行者对三个层次的选择肢的无差异阈值均为10，即Δm=Δh=Δk=10。假设两种情形中出行者在交通出行行为选择的三个层次中均无偏好，即0.5。根据式（1）、式（13）～（15）对上述算例进行建模，由MATLAB 算得所构建的多级网络模型能够达到收敛条件。流量计算结果如表4、表5所示。

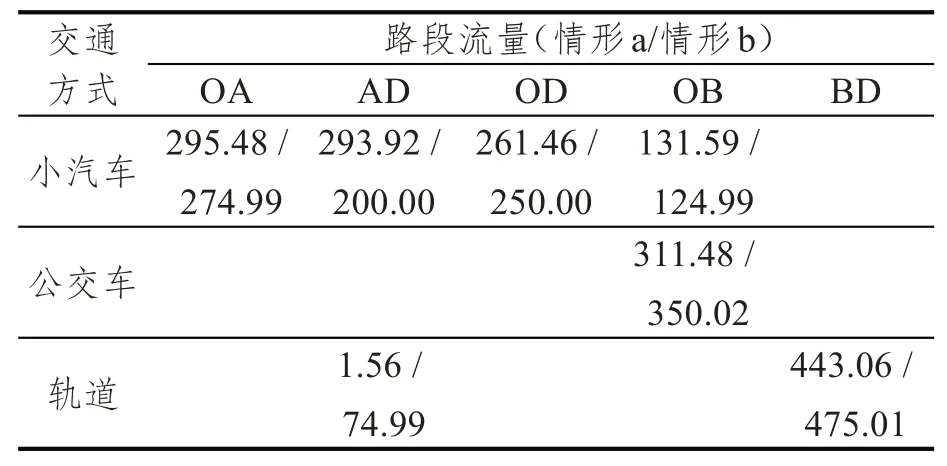
表4 平衡状态下路段流量表Tab.4 Flow tables for road links in the equilibrium

表5 平衡状态下路径流量表Tab.5 Flow tables for paths in the equilibrium

根据计算结果，方案5中公交车换乘轨道交通的路径流量最大，这表明在初始状态下，方案5 的出行效用最大。从交通方式选择来看，大多数出行者选择小汽车出行，这是因为当公共交通线路的人流量超出了车辆的座位数甚至是载客量时，会出现拥挤情况，导致额外的出行阻抗。因此，出行者选择小汽车出行以获得更高的出行舒适度。对比表5 中a、b两种情形发现，在情形a下，小汽车出行的流量比重较高，约占总需求的56%；在情形b 下，小汽车出行的流量比重下降，组合交通出行的比重更高，约占总需求的55%，这说明出行者在考虑无差异阈值和不考虑无差异阈值时的选择是不同的，在此算例中当单一交通方式与组合交通方式的出行效用差小于出行者能感知的无差异阈值时，组合交通方式更容易被选择。因此，这证实了考虑无差异阈值的模型会影响组合交通方式的选择分担，并验证了该模型的效果。引入无差异阈值的概念可以更好地反映出行选择过程中的随机性。

绘制不同选择方式随Δm的变化情况，如图6所示。首先令无差异阈值Δh=0,Δk=0，偏好参数=0.5,τk=0.5，即出行者对换乘点选择、路径选择能做到完全理性且均无偏好，对交通方式选择无偏好。

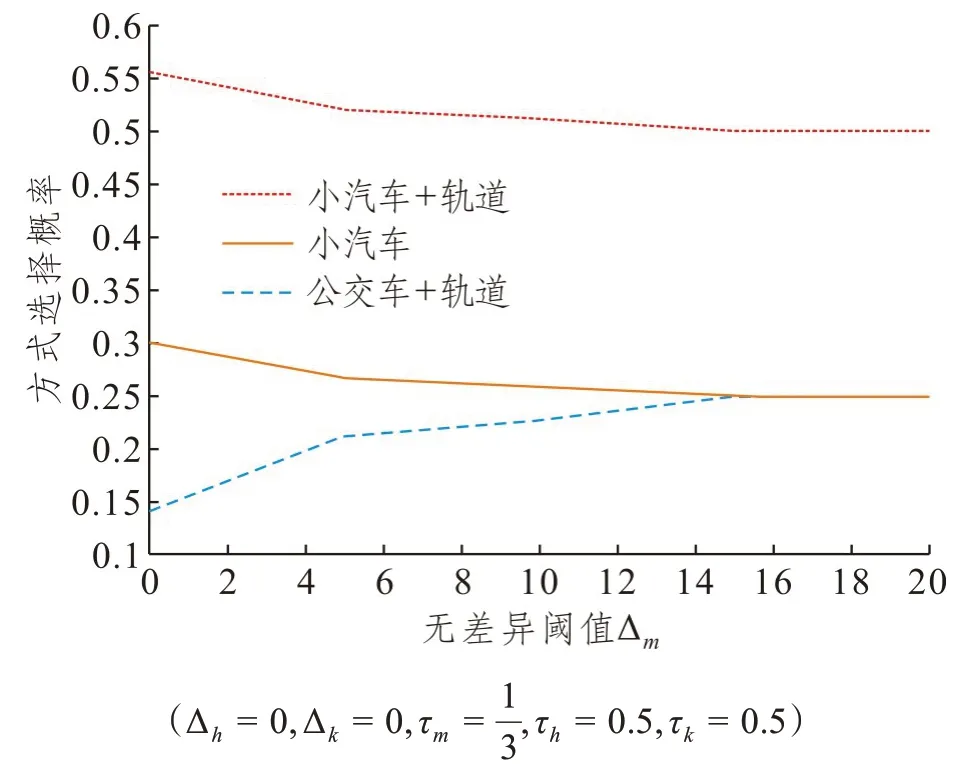
图6 无差异阈值Δm与方式选择概率关系Fig.6 Relation between the indifference threshold Δm and the probability of travel mode choice

当Δm=0 时，模型退化为传统的Nested Logit模型，当Δm不为0 时，模型为基于无差异阈值的Nested Logit模型。

图6 中可以看出Δm对不同方式选择概率的影响较大，随着Δm的增加小汽车与公交接驳轨道出行选择概率降低，小汽车接驳轨道出行方式选择概率增加。并且小汽车出行选择概率逐渐降低到50%，小汽车接驳轨道出行与公交车接驳轨道出行两种组合出行方式选择概率逐渐接近，说明出行者在交通出行行为选择的三个层次均无偏好时，当Δm即交通方式选择的无差异阈值足够大时，其选择趋于随机。

出行者对交通方式选择、路径选择能做到完全理性且均无偏好，对换乘点选择无偏好时，不同选择方式随Δh的变化情况如图7所示。

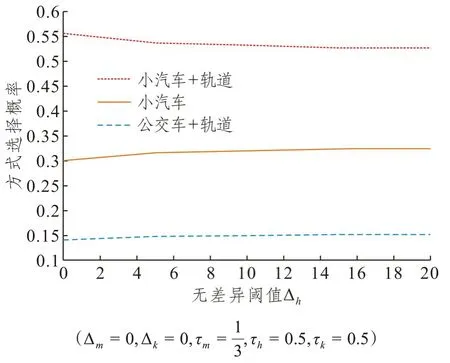
图7 无差异阈值Δh与方式选择概率关系Fig.7 Relation between the indifference threshold Δh and the probability of travel mode choice

随着Δh的增加小汽车出行选择概率降低，组合出行方式选择概率增加，说明交通出行行为中下层的无差异阈值影响上层的选择概率。相较于Δm，Δh对不同方式选择概率的影响较小，说明模型下层的无差异阈值对上层的选择概率影响有限。

出行者对交通方式选择、换乘点选择能做到完全理性且均无偏好，对路径选择无偏好时，不同选择方式随Δk的变化情况如图8所示。

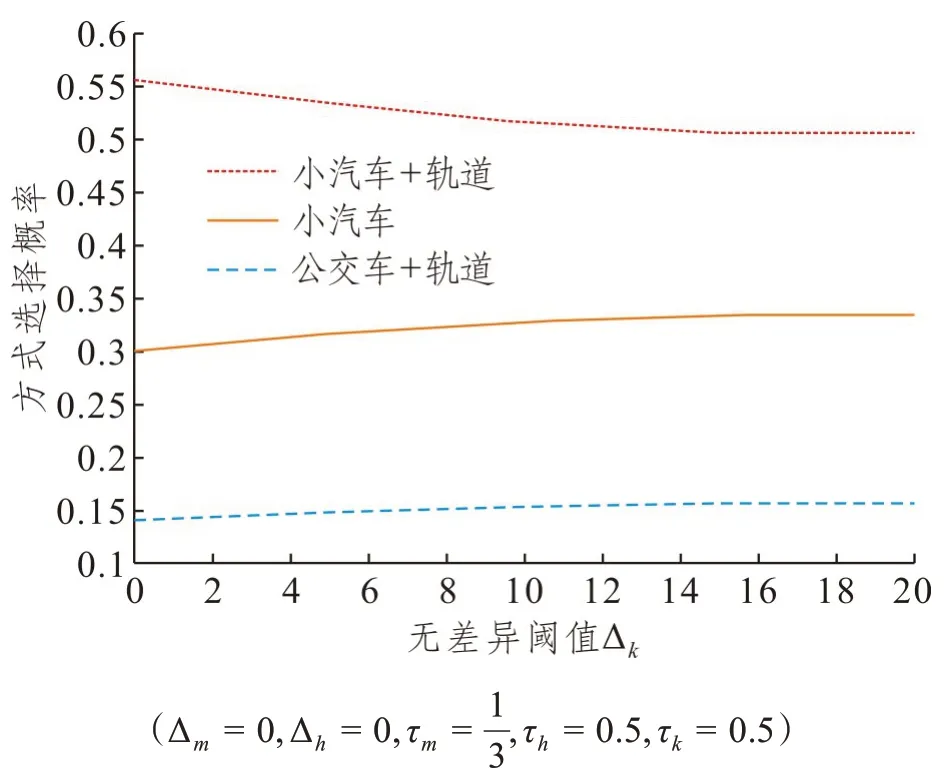
图8 无差异阈值Δk与方式选择概率关系Fig.8 Relation between the indifference threshold Δk and the probability of travel mode choice

可以看出，随着Δk的增加小汽车出行选择概率降低，而小汽车接驳轨道出行的组合出行方式选择概率增加。这种变化趋势与图7相似，但变化程度较图7略大。这表明在该算例中，路径选择的无差异阈值相比换乘点选择的无差异阈值对交通方式选择概率的影响更大。因此，通过改善乘点与路径选择层级的选择环境，可以在一定范围内优化各交通出行方式的分担比率。

在实际情况下，减小无差异阈值可以增加交通方式的确定性，并有助于多模式出行路径的客流预测。提高组合交通方式的分担比例，可以引导居民选择更为绿色的出行方式。一方面，当单一交通方式与组合交通方式的效用差绝对值在无差异阈值范围内时，可以通过加强宣传、信息引导等手段提高公众对组合交通出行的认知，增强出行者对组合交通的偏好，减少出行者对小汽车出行的惯性选择。另一方面，应通过提高组合交通出行方式的服务水平，例如改善信息互通、增加发车频率、改善换乘衔接等措施，提高其绝对效用，增加选择组合交通方式的确定性。