基于Stackelberg博弈的公共停车场停车收费定价模型构建

2023-12-12李聪颖任博冉周勋朝张洪涛张大鹏贾锦绣

交通运输工程与信息学报 2023年4期

李聪颖，任博冉，周勋朝*,2，张洪涛，张大鹏，贾锦绣

(1.西安建筑科技大学，土木工程学院，西安 710055；2.隆基绿能科技股份有限公司，西安 710100；3.中国人民大学，公共管理学院，北京 100872；4.西安市政设计研究院有限公司，西安 710068)

0 引言

面对城市日益突出的停车问题，停车收费是一种有效提高停车资源利用，缓解停车问题的交通管理方法，合理的停车收费定价有利于私家车出行者做出合适的停车行为选择、停车场管理者增加利润及促进停车需求在时间和空间上的合理分配。2021 年国家发展改革委等四部委发布的《关于推动城市停车设施发展的意见》提出要“完善停车收费政策，健全主要由市场决定价格的停车收费机制，逐步缩小政府定价范围”。我国部分城市目前停车收费定价存在管理松散，运营者一刀切的情况，停车收费定价在私家车出行者、停车场运营者、交通管理者三方中难以达成共识。如何协调三方间利益诉求，制定合理的停车定价，满足私家车出行者节省出行成本、停车场运营者盈利相对最大、交通管理者社会负效用最小的目的，成为一个重要的研究问题。

针对停车收费定价对私家车出行者、停车场运营者、交通管理者三方的影响，已有研究主要集中在改变停车行为、提升停车场运营利润和公交分担率等方面。贺康康等[1]基于动态定价停车预约意愿问卷和驾驶人个人属性等数据构建了巢式Logit 模型，确定了停车预约费率对驾驶人出行行为选择有显著影响；李浩等[2]探究弹性工作制与动态停车收费的组合管理策略，构建了基于出行分布及动态停车收费费率的双层规划模型，结果表明组合策略更有助于缓解交通拥堵；Hensher 等[3]对悉尼CBD 地区的部分停车场进行了调查，提出提高停车收费价格将增加公共交通使用比例，并显著影响私家车出行者停车位置选择；徐红利等[4]以考虑共乘激励的交通流分配和停车收费策略为切入点构建停车收费模型，提出合理的停车收费和共乘激励可以显著增加出行者参与共乘的意愿，增加共乘匹配成功的人数；胡晓伟等[5]分析城市停车PPP 项目中各参与主体的利益诉求，构建了针对PPP 项目公司、政府方和停车用户三方不同的期望定价下的目标规划模型；Proulx 等[6]通过调查加利福尼亚大学的通勤出行行为，认为公共交通票价和停车收费费率都会影响出行行为选择，其中影响最大的是停车收费费率；王建军等[7]提出停车定价方法不仅需要考虑停车者和经营者的利益，也需考虑社会公众的需求，基于公交分担率研究分析最优定价机制。研究表明停车收费费率对出行者出行方式选择、出行行为选择、交通需求有较为显著的影响。

近年来博弈论在交通研究中的应用日益广泛，关于博弈模型的研究主要包括对博弈模型求解算法的研究、对公共交通系统的应用研究、对拥挤收费的应用研究，以及对停车收费的应用研究等。在应用博弈论制定停车收费策略的研究中，通常选取出行者目标或者停车场运营者目标，通过合理设定各个目标的相对权重，构建交通管理者管理目标，调节停车供需平衡。Tsai 等[8]构建了停车收费定价博弈模型，研究了当政府管理部门拥有停车泊位时，政府管理部门和停车场经营商共同经营的停车场收费定价问题；Qian 等[9-10]从经济学角度分析了私营停车场的特点，建立了完全市场条件下基于早高峰出行停车收费管理的4 种均衡，讨论了通过市场竞争的停车收费政策可以最大限度减少社会成本；朱成娟等[11]考虑私人运营商追求运营利润最大和政府追求社会总成本最小的特性，构建了博弈模型研究停车位分配策略和停车费定价问题；王瑜琼等[12]基于FSC 效用函数建立了三阶段的停车收费博弈模型，求解停车收费过程中收费人员和停车者讨价还价区间。已有研究表明参与停车收费定价的各方参与者可以通过建立博弈模型调节停车收费费率，进而达到自己利益诉求的目的。

综上，国内外部分学者研究了停车收费费率对出行者出行选择、停车场运营利润、公交出行比例等方面的影响，分析了停车收费定价对私家车出行者的影响。探究私家车出行者、停车场运营者及交通管理者三方在停车收费定价中的影响关系及各自的利益诉求，可为公共停车场制定停车收费策略提供参考依据。

本文分别考虑私家车出行者、停车场运营者和交通管理者的各方利益，从博弈理论的角度分析三方停车参与者之间的交互关系，构建公共停车场停车收费定价模型，探讨三方共同参与停车收费定价条件下整体最优的停车收费定价策略。

1 停车定价三方参与者博弈关系

私家车出行者、停车场运营者及交通管理者是停车定价的三个参与方，对公共停车场定价具有决策权。在停车价格决策中，三方参与者通常会选择使其自身成本最小化或利益最大化的决策，找到使各自达到最优的方案，寻求三方参与者各利益主体间利益矛盾最小的方案，是停车收费定价需要解决的问题。

效用理论是经济学中典型的决策理论，是决策者对其决策后果的主观评判，它以数学函数量化决策者对其决策后果的满意度[13]。停车系统中交通管理者制定停车收费方案，停车场运营者提供停车服务，私家车出行者选择路径和停车场。基于三方的决策行为，本文模拟停车收费定价参与者的心理活动，为每个决策行为确定一个效用值，假设参与者选择效用值最大即满意度最高的决策行为，为采用博弈论构建停车收费价格定价模型构建提供基础。

博弈论是研究两个以上决策主体的相互性决策以及决策均衡性问题的理论与方法[14]。博弈论的构成要素包括：参与者集合、策略集合和策略收益集合。本文研究停车定价问题中，参与者集合为公共停车场收费定价参与三方，包括：私家车出行者（驾驶员）、停车场运营者（企业）和交通管理者（管理部门）。基于效用理论，策略集合为三方停车收费定价参与者选择的各自最优的策略，策略收益集合为量化各方策略利益的函数集。

停车服务链中的三方参与者之间存在既对抗又合作的关系，三方参与者互相博弈促使各方参与者需要考虑总体效益，达到各方参与者相对利益最大，减少因参与者之间利益冲突导致的整个停车服务链的利益损失。涉及的博弈问题是三方参与者博弈下的停车收费费率优化，三方参与者博弈关系如图1所示。

图1 三方参与者博弈关系Fig.1 Game relationship between three participants

从停车收费定价参与者角度分析，私家车出行者为三方博弈中的下层，停车费率、寻泊时间等指标反映了私家车出行者的经济、时间成本大小。私家车出行者以出行效用最大化为目标作出停车行为选择，决策信息反馈给停车场运营者和交通管理者。

停车场运营者为三方博弈中的中层，与私家车出行者以有序的非合作方式相互作用，也与三方博弈中的上层互相影响，即遵守交通管理者发布的停车收费政策，同时反馈信息给交通管理者以改进收费政策。

交通管理者为三方博弈中的上层，通过道路饱和度和停放饱和度指标反映交通资源是否得到合理利用，得到交通管理者社会负效用模型，制定停车收费方案引导或约束私家车出行者和停车场运营者的决策行为，量化道路状况与交通设施给私家车出行者、停车场运营者造成的负面影响。

三方参与者博弈过程是私家车出行者、停车场运营者和交通管理者以停车收费价格直接或间接影响对方的行动，进而得到对自己最有利的结果的过程，本文基于效用理论运用博弈论重现这一动态作用过程。

2 停车场参与者决策行为

在三方参与者仅考虑自身利益指标的前提下，各方参与者均会进行各自利益最大化决策行为，基于效用理论构建三方参与者各自利益最大化的行为选择模型，为三方参与者进行停车收费费率定价博弈提供理论基础。

2.1 出行者停车行为选择模型

停车行为是私家车出行者在寻找和选择车辆停放场所的过程中产生的一系列决策行为。私家车出行者驾车从起点到终点附近后，可以有多个停车场进行选择，因而从起点到不同停车场之间存在多条路径。对于私家车出行者而言，需要经历三个过程：驾车在道路上行驶的过程；接近目的地选择停车场停车的过程；停车后从停车场步行到终点的过程。

私家车出行者从起点O出发驾车去终点D，在终点附近有h个停车场可供其选择，从起点到停车场k之间存在多条路段l，停车行为选择过程如图2所示。

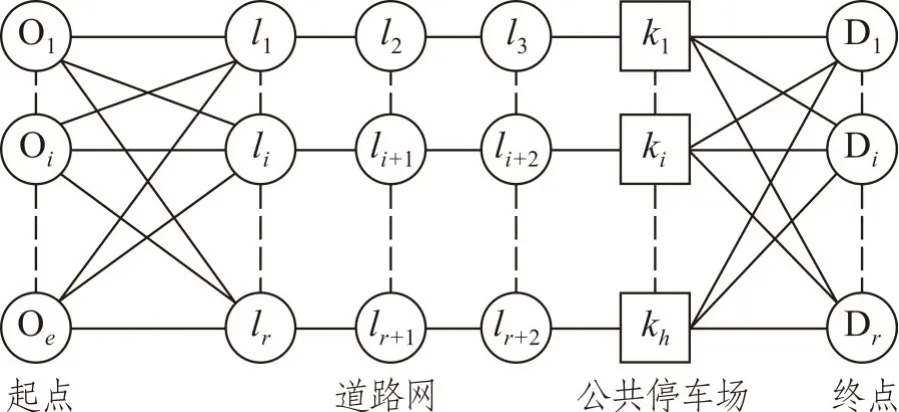
图2 停车行为选择过程Fig.2 Process of parking behavior selection

由图2可以看出，路段选择和停车场选择之间存在多种组合方式，组成起点O 到终点D 间的多条行驶路径L，私家车出行者从起点O 到终点D 选择停车场k的出行成本CkΟDL为：

式中：y为每辆小汽车单位时间出行成本，元/h；tkΟL为起点O 至停车场k行程时间，h；tk为在停车场k寻找泊位时间，h；tkD为停车场k到终点D 步行时间，h；uVOT为私家车出行者单位时间价值，元/h；n为平均车载人数，取1.3；fk为私家车出行者在停车场k的停车费，元。

下层规划模型描述了私家车出行者基于成本最小化的停车行为选择模型，私家车出行者选择出行成本最小的路径，本文构建的下层规划模型为：

式中：C为私家车出行者的总出行成本，元；VL为行驶路径L上到达停车场的交通量，pcu/h。

2.2 停车场运营者运营利润模型

从停车场运营者角度来看，其根据停车需求优化停车收费费率，提升停车场服务吸引力。在停车场市场化运营环境下，提高停车收费费率将减少私家车出行者停车需求[15]，停车场运营者的运营利润会在一定程度上降低。根据停车场服务能力优化停车收费费率，为私家车出行者提供停车泊位服务，以运营利润最大作为停车场运营者目标，即停车费收入减去停车场成本得到的最大值。停车场运营者的运营利润计算公式如下：

式中：zk为停车场k的运营利润，元；qk为停车场k的停放泊位数量，个；ckg为在停车场k单位时间停车泊位成本，元/h；tkp为在停车场k的平均停放时间，h。

中层规划模型描述如何申请优化停车收费费率，以实现研究区域内所有停车场运营者的总运营利润最大，本文构建的中层规划模型为：

式中：Z为公共停车场的总运营利润（元）。

2.3 交通管理者社会负效用模型

交通管理者通过停车收费引导私家车出行者的停车行为，调配停车需求的时空分布，调节停车供需平衡，均衡动态交通网络，进而促进公共停车场保持最佳停放饱和度，路网保持最佳道路饱和度，达到社会负效用最小的目的。最佳停放饱和度能有效减少小汽车寻泊时间，避免供需失衡；最佳道路饱和度能降低小汽车之间相互干扰，降低运行延误。交通管理者目标模型的向量U具体表达式如下，计算方法为：

式中：U1为公共停车场的实际停放饱和度和最佳停放饱和度之差；λn与λm分别为最佳停放饱和度下限和上限；nk为停车场k容量；U2为路网的实际道路饱和度和最佳道路饱和度之差；θn与θm分别为最佳道路饱和度下限和上限；Vl为路段l的交通量，pcu/h；Cl为路段l的实际通行能力，pcu/h。

上层规划模型描述如何制定停车收费费率，以实现停车供需平衡和均衡动态交通网络，使社会负效用最小，即停放饱和度和道路饱和度处于一定范围，保证停车泊位资源和道路资源有效利用。本文构建的上层规划模型为：

式中：U为交通管理者期望的公共停车场停放饱和度与道路饱和度。

3 停车收费定价模型

Stackelberg 博弈模型引入了决策者选择策略的先后次序，领导者先选择策略，跟随者根据领导者的策略决定自己的选择，领导者根据跟随者的选择调整自己的策略。在理性条件下，参与者会对任何变化做出最优反应。如此往复，最终达到参与者的混合策略收益最大化的目的。

基于Stackelberg 博弈模型描述停车收费定价问题本质上是私家车出行者、停车场运营者和交通管理者决策三方收益目标相互靠近的过程，揭示不同利益矛盾、不同决策行为选择及其影响下各参与方对停车收费定价的促进和抑制作用，使停车收费定价策略不断向稳定状态演化。

3.1 基于Stackelberg 博弈的停车收费定价模型建立

停车收费定价模型考虑多个目标对公共停车场停车收费定价的影响，在约束条件下实现整体的优化。交通管理者是上层的领导者，以社会负效用最小为目标；停车场运营者是中层的跟随者，以运营利润最大为目标；私家车出行者是最下层的跟随者，以出行成本最小为目标。模型构建目标为出行成本低、运营利润大以及社会负效用小，具体模型为：

将私家车出行者、停车场运营者和交通管理者视为博弈过程中的三方参与者，运用Stackelberg博弈实现三方利益上的共赢。这种共赢不同于用户最优或者系统最优，参与者在决策前考虑个人利益最大化，在决策过程中同时考虑了其他参与者的反应。私家车出行者、停车场运营者和交通管理者之间进行博弈，达到令三方都满意的稳定解时博弈结束。此博弈为完美信息博弈，寻找的稳定解是私家车出行者、停车场运营者和交通管理者的一个策略组合。

3.2 基于Stackelberg 博弈的停车收费定价模型参数

（1）小汽车单位时间成本

小汽车出行直接支出的费用为停车费用以及燃油消耗，本文选取停车收费价格作为私家车出行者出行成本的影响因素，故采用燃油消耗量化小汽车单位时间成本y[16]，平峰时段y1为：

式中：ν为小汽车平均行驶速度，km/h；Ρo为燃油价格，元/L。

（2）起点到停车场行程时间

起点到停车场行程时间包括路段行程时间和通过交叉口时间tkΟL[17]，计算方法为：

式中：tkΟl为路段行程时间，h；tj为通过交叉口时间，h。

路段行程时间tkΟl采用BPR路阻模型计算[18]公式为：

计算通过交叉口时间tj[18]为：

式中：t1为均匀延误时间；t2为过饱和延误时间；T为信号周期长度，s；ε为绿信比；X为道路饱和度；S为进口道实际通行能力，pcu/h。

（3）寻找停车泊位时间

寻找停车泊位时间由停车场的停车泊位占用率tk[19]表示：

（4）停车场到目的地步行时间

停车场到目的地步行时间tkD由停车场到目的地的距离与私家车出行者步行速度的比值表示：

式中：lkD为停车场k到终点D的距离，km；νb为私家车出行者步行速度，km/h。

（5）私家车出行者单位时间价值

交通出行中的时间成本uVOT是出行时间的货币化表现[20]，由出行者年均收入与年均工作小时数的比值确定：

式中：Ν为停车场所在地区居民年均收入，元；W为停车场所在地区居民年均工作小时数，h。

（6）停车收费价格

交通管理者指导停车收费定价方案，停车收费费率在规定的上限和下限之间，上限为交通管理者规定的最高限价，下限为停车场单位停车泊位成本。本文采用的分时段累进制方法是目前停车场中使用较广的收费方法，即规定一段免费停放时间，超出此时限将开始计时收费，表示为：

式中：tmin为停车场k免费停放时间，h；pk为停车场k的停车收费费率，元/h；pkmin与pkmax分别为停车场k停车收费费率的下限和上限，元/h。

3.3 Stackelberg博弈稳定策略求解算法

算法基本思想：在私家车出行者、停车场运营者和交通管理者的Stackelberg 博弈中，每个参与者决策集的最优决策集合在一起，该决策集构成了最优策略的集合，稳定策略是所有参与者最优策略的组合，无论哪一方都不能单方面改变策略以获得更大效用时，就确定了三方之间的稳定策略。这是多阶段完美且完全动态信息博弈，以迭代过程求解私家车出行者、停车场运营者和交通管理者之间的Stackelberg 博弈，达到三方之间的稳定解，算法步骤如下：

Step2 初始化。令迭代次数n′=1，获得已标定的相关参数，交通管理者制定停车收费费率pk。

Step3 选择停车行为。根据交通管理者制定的停车收费费率pk，私家车出行者i′选择出行成本CkΟDL(i′)最小的停车行为，路网产生新的流量分布，更新不同路径和公共停车场的出行成本CkΟDL，第i′+1 个私家车出行者的选择受到第i′个私家车出行者影响。基于出行成本最小选择停车行为，得到路段交通量Vl(1)和公共停车场停放数qk(1)。

Step4 结果计算。计算私家车出行者的总成本C(1)，停车场运营者的总运营利润Z(1)，交通管理者的社会负效用U(1)。

Step5 交通管理者基于新的流量分布，重新制定停车收费费率pk，令n′=n′+1，转至Step2，进行下一轮的停车收费定价。

Step6 计算在不同的停车收费费率pk时，私家车出行者的总出行成本C(i)，(i=1,2,…,n′)，得到解集C0=(C(1),C(2),…,C(n′))；停车场运营者的总运营利润Z(i)，(i=1,2,…,n′)，得到解集Z0=(Z(1),Z(2),…,Z(n′)；交通管理者的社会负效用U(i)，(i=1,2,…,n′)，得到解集U0=(U(1),U(2),…,U(n′))。

Step7 稳定判断。若满足收敛准则，即三方策略间的误差率在允许范围ξ之内，则得到了令三方都满意的稳定解，已经达到博弈稳定的状态。三方参与下Stackelberg 博弈稳定算法收敛准则表达式为：

4 实例应用

为了验证以上模型及求解算法的有效性，选取陕西省咸阳市两个临近公共停车场为研究对象，展开停车收费研究。数据来源包括咸阳市统计局官网和停车调查。

4.1 研究区域背景

根据停车场理想服务半径L不宜超过200 m[21]，选定出行起点O 和终点D，对OD 间路径和以终点D 为圆心，半径200 m 内两个公共停车场进行研究，两个公共停车场位于城区中心区，周边集聚了学校，商业设施和休闲场所。公共停车场A和B位置及周边道路如图3所示。

图3 停车场位置及周边道路示意图Fig.3 Schematic map of parking lot location and surrounding roads

起点O 至终点D 途经交叉口共8 个，终点D 步行可达范围内共两处公共停车场；起点O 至公共停车场A、B 行驶路段共11条，为路段1至路段11；公共停车场A、B 至终点D 步行路段2 条，为路段12、路段13路侧人行道。

4.2 交通状况参数计算

针对OD 点间道路进行高峰时段路段交通量、通行能力、路段自由行驶时间调查，得到OD 点之间可选行驶路段基本交通参数，如表1 所示。实地调查OD 点之间途经交叉口信号配时及道路设施条件，得到不同交叉口基本交通参数，如表2所示。

表1 OD之间路段交通参数Tab.1 Basic traffic parameters for road segments between origin and destination

表2 OD之间交叉口基本交通参数Tab.2 Basic traffic parameters for intersections between origin and destination

选定的OD 点之间基于周边路网产生7 条可选行驶路径，如表3所示。通过对研究区域内的公共停车场实地调查，公共停车场参数如表4 所示。停车收费定价模型中其余相关参数如表5所示。

表3 OD之间可行路径Tab.3 Possible paths between origin and destination

表4 公共停车场参数Tab.4 Public parking parameters

表5 停车收费模型相关参数Tab.5 Calculation results of related parameters of parking charging model

根据2021 年6 月咸阳市92 号汽油价格，燃油价格Ρo取平均值为6.88 元，小汽车行驶速度ν取40 km/h，由公式11 计算得小汽车单位时间成本y为27.77 元/h。咸阳市2020 年城镇非私营单位在岗职工年均收入Ν为69 290 元[22]，法定工作日共251 天，一天工作8 小时制，年均工作小时数W为2 008 h，由公式19 计算得到私家车出行者单位时间价值uVΟT为34.51元/h。

停车场服务成本包括停车场的土地、建造、设备和经营成本，服务成本可以作为路边停车收费费率的下限[23]，参考停车场停车泊位尺寸等有关参数，根据备选公共停车场停车泊位成本和平均停放时间，本文pkmin取1 元/h。安实等[24]提出对于路外停车场，当停车场收费费率低于9 元/h 时，出行者接受度为98.7%，本文pkmax取9元/h。

当道路饱和度V/C＞0.8 时，道路的交通运行状况处于交通拥挤状态，一般城市道路采用三级服务水平设计[25]，本文θn与θm分别取0.35 和0.54。对于城市中心区，停放饱和度λ在0.7～0.8 之间比较理想，超过0.95 时，车辆进出泊位频繁且速度很慢，降低了停车场的运营效率[26]，本文λn与λm分别取0.7和0.8。

将上述参数代入，得到公共停车场停车收费模型为：

4.3 停车收费定价模型稳定解计算

根据求解算法，基于Java8 编写程序，求解停车收费定价模型稳定策略。编码变量为停车场收费费率，基于现有部分停车场收费费率调查，最小值为1 元/h，最大值为9 元/h，迭代步幅长度取0.1，误差范围取0.000 01，对所求结果导入MATLAB(R2014b)绘制三维图。计算私家车出行者在不同收费费率下的总出行成本C，计算结果如图4 所示，私家车出行者最优策略是总出行成本C最小，即为图4中最低点。

图4 总出行成本变化图Fig.4 Total travel cost change chart

从图4可以看出，当停车场A收费费率为9元/h，停车场B 收费费率为2.6 元/h，私家车出行者的总出行成本之和最低，minC为7 530.78 元。此方案下停车需求数量210 个，选择停车场A 和B 的私家车出行者分别为10 个和200 个；两个公共停车场的总运营利润之和为3 208.73元；两个公共停车场的停放饱和度与期望值差距之和为0.87，可选路径上所有道路的饱和度与期望值差距之和为1.38，此为停车收费定价方案1（出行者总出行成本最小方案）。

计算停车场运营者在不同收费费率下的总运营利润Z，计算结果如图5 所示，停车场运营者最优策略是总运营利润Z最大，即为图5 中最高点。

从图5 可以看出，当停车场A 收费费率为5.7元/h，停车场B 收费费率为6.6 元/h，两个公共停车场的总运营利润之和最高，maxZ为7 902.08 元。此方案下停车需求为231 个，选择停车场A 和B 的私家车出行者分别为119 个和112 个；231 个私家车出行者的总出行成本之和11 949.56 元；两个公共停车场的停放饱和度与期望值差距之和为0.56；可选路径上所有道路的饱和度与期望值差距之和为1.43，此为停车收费定价方案2（公共停车场总运营利润最大方案）。

计算交通管理者在不同收费费率下的社会负效用U，计算结果如图6和图7所示，交通管理者最优策略是社会负效用U最小，即为图6 和图7 中最低点。

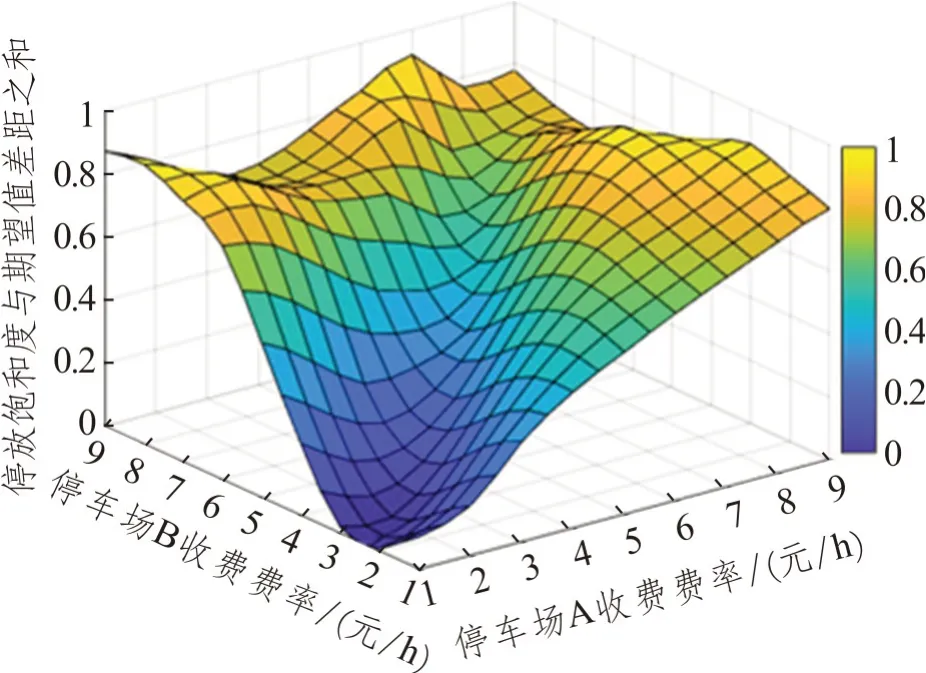
图6 停放饱和度变化图Fig.6 Parking saturation change chart

图7 道路饱和度变化图Fig.7 Road saturation change chart

从图6 可以看出，当停车场A 收费费率为1.9元/h，停车场B收费费率为3.1元/h，两个公共停车场的停放饱和度与期望值差距之和最小，minU1为0，最接近期望值λ∈[0.7,0.8]的范围。此方案下停车需求为393 个，选择停车场A 和B 的私家车出行者分别为250 个和143 个；393 个私家车出行者的总出行成本之和12 613.30 元；两个公共停车场的总运营利润之和为4 781.63元；可选路径上所有道路的饱和度与期望值差距之和为1.73，此为停车收费定价方案3（公共停车场停放饱和度与期望值差距之和最小方案）。

从图7 可以看出，当停车场A 收费费率为8 元/h，停车场B 停车收费费率为8.9 元/h，所有路段的道路饱和度与期望值差距之和最小，minU2为1.23，最接近期望值θ∈[0.35,0.54]的范围。此方案下停车需求为146 个，选择停车场A 和B 的私家车出行者分别为36 个和110 个；146 个私家车出行者的总出行成本之和9 983.07 元；两个公共停车场的总运营利润之和为7 110.67元；两个公共停车场的停放饱和度与期望值差距之和为0.75，此为停车收费定价方案4（道路饱和度与期望值差距之和最小方案）。

私家车出行者、停车场运营者和交通管理者在不同的收费费率下会达到各自的最优策略。计算停车收费定价模型稳定解的收敛函数，当其达到最小值minϕ(p)时，得到的计算结果最接近三方各自的最优策略。minϕ(p)<ξ对于任意有可行解的ξ都满足收敛条件，根据收敛条件，计算收敛函数最小值：

当停车场A 和B 收费费率分别为4.5 元/h 和3.9 元/h 时，ϕ(p)达到最小值，最接近三方各自的最优策略，此方案下停车需求为303 个。选择停车场A 和B 的私家车出行者分别为136 个和167 个，303 个私家车出行者的总出行成本之和为12 999.41 元；两个公共停车场的总运营利润之和为6 902.17元；公共停车场的停放饱和度与期望值差距之和为0.35；可选路径上所有道路的饱和度与期望值差距之和为1.51，此为停车收费定价方案5（三方博弈下定价方案）。

三方参与者各自利益最大化的停车收费定价方案和三方博弈下的停车收费定价方案如表6所示。

表6 各停车收费定价方案Tab.6 Pricing schemes for each parking fee

方案1出行者总出行成本为五个方案最小，私家车出行者的总出行成本之和为7 530.78元；方案2 公共停车场总运营利润为五个方案最大，总运营利润之和为7 902.08 元；方案3 停车场停放饱和度与期望值差距之和为五个方案最小，停车场停放饱和度与期望值差距之和为0；方案4 道路的饱和度与期望值差距之和为五个方案最小，道路的饱和度与期望值差距之和为1.23；方案5 私家车出行者的总出行成本之和为12 999.41 元，公共停车场总运营利润之和为6 902.17元，停车场饱和度与期望值差距和以及道路的饱和度与期望值差距和分别为0.35、1.51，较好满足三方利益需求。综上，方案5（三方博弈下的定价方案）是三方参与者共同参与停车收费定价下各利益主体间利益矛盾最小的停车收费定价方案。