基于贪婪最佳优先搜索算法的方形件排样优化问题研究

刘艳丽，李军祥 （上海理工大学管理学院，上海 200093）

0 引 言

受益于我国良好的制造业基础及政府对制造业智能化转型升级的大力推动，近年来智能制造行业的发展较为迅速。智能制造装备具有分析、推理和感知等功能，它是智能技术、信息技术和先进制造技术的集成和深度融合[1]。随着生产技术的发展，在工业4.0 的数字化转型背景下，众多企业开始以个性化定制和供应链整合为切入，实现以用户为中心的大规模个性化定制[2]。当前在新一代数字科技的支撑和引领下，越来越多新兴的智能制造企业开始进行数字化升级、转型和再造，建设数字化智能工厂，提升智能制造能力和个性化定制能力，使得在面对用户需求时能够做到快速响应、有效应变。

方形件产品是指采用板材为主要用料，经过一系列程序加工后生成板式配件，再按照图纸进行组装后形成的一类产品[3]。这类产品多用于制造企业，主要面向包括通讯设备、精密机床制造、消费性电子、金属板材等产业的多个领域。为了保量和以最小化的成本制造满足顾客需求的个性化产品，智能制造企业大多采用多品种、小批量和个性化定制方式进行生产，采用“订单组批+批量生产+订单分拣”的模式，通过订单组批来实现批量切割以更好地发挥规模效益，再整合订单中的共同需求得到不同客户的拣取信息进行订单分拣[4]。

其中，个性化定制生产模式涉及排样优化这一关键性问题。排样优化本质上是一个下料问题，是指将一系列方形件按最优方式在板材上进行排布，要求方形件排放在板材内，各个方形件互不重叠，并满足一定的工艺要求。优化的目标是生成最合理的排样方式，最大限度地节约材料、提高材料利用率，实现切割过程的简化。该问题是一个组合优化问题，计算复杂度很高，也是运筹学领域一个非常重要的分支。许多制造企业生产产品和零部件的第一步即下料，过程中会消耗大量的材料和资源，如果不合理规划则会造成巨大的浪费。因此，本文构建了一个排样优化模型，考虑了一系列相关约束，利用贪婪最佳优先搜索算法对模型进行求解，针对各数据集给出其最佳的排样效果图，验证了模型的有效性及可行性。

1 问题描述及假设

1.1 排样优化问题描述

本文采用3 阶段切割方式，要求只能进行齐头切且每个阶段只能选择一个方向进行切割。齐头切也称“一刀切”，要求每次进行直线切割时板材都能分成两块[5]。3 阶段切割方式如图1 所示，第1 阶段进行横向切割，此时生成的模块称为Stripe（条带），如Stripe1 和Stripe2；第2 阶段进行纵向切割生成的模块称为Stack（栈），如Stripe1 被切割分成Stack1、Stack2 和Stack3；接下来进行第三阶段的横向切割，生成的模块称之为Item（产品项），如Stack1 继续被分成Item1、Item2 和Item3。本文基于以上规则对方形件进行切割。排样优化问题属于二维组合优化问题，通过研究方形件在板材上的排放顺序和排放方式，使得方形件在板材上组合排放的利用率达到最高。具体来说就是根据同一个生产排次内的方形件尺寸和数量进行原片规格和数量的选择。该问题要求在满足生产订单需求和相关约束条件下，进行下料排样优化，尽可能减少板材用量，避免浪费，使板材原片的利用率达到最大。其中需要考虑的约束条件如下：（1） 在相同栈里的产品项的宽度（或长度） 应该相同；（2） 最终切割生成的产品项是完整的，非拼接而成。该问题本质上是一个二维装箱问题，也就是将若干个矩形物品装进矩形的箱子中，并且在装箱的过程中不允许将矩形物品斜着放，必须平行于横坐标。一般来说求解的目标是使箱子的数目或者是空间占用率最小。当用于矩阵存储时，求解的最优目标便是箱子的空间占用率最大化。

图1 不同切割阶段的形式定义

1.2 假设与约束条件

（1） 只考虑齐头切的直线切割方式，切割方向均垂直于板材的一条边，且每次切割板材都可以分成两块；

（2） 切割阶段数不超过3，且同一个阶段的切割方向相同；

（3） 排样方式为精确排样，即在三个阶段内能切割出准确尺寸的方形件；

（4） 板材原片只有一种规格并且数量充足；

（5） 排样方案不考虑切割缝隙宽度的影响。

2 排样优化模型构建

方形件排样优化问题用数学语言可以描述为：将n个不同规格的方形零件{k1,k2,…,kn}排入到一个宽度为M，长度L的板材原片中，且板材原片数充足，待排样的毛坯有m种，长、宽、高需求量分别为（li,wi,di），其中i为毛坯型号。B={1,2,…,b}是一个由b个相同的方形件组成的集合，stack（k∈B）的宽度为W，高度为H。N={1,2,…,n}是一个由n个item组成的集合，其中n≥b。

设板材原片左下角为原点（0,0），左上角为（0,M），右下角为（L,0），x和y表示item在其分配的stack内的位置，即方形件ki的左上角坐标为（xi,yi），其中xi≥0，yi≥0，i∈N*。第i个item（i∈N）的宽度wi≤W，高度hi≤H，若ki旋转了90°，则其宽度和高度互换，ri为是否旋转变量，ri=1 表示旋转，ri=0 不旋转，则ki右下角坐标为（xi+（1-ri）wi+rihi,yi-（1-ri）hi-riwi）。N*表示由旋转的重复项附加的集合N，第i个item（i∈N）的重复项是宽度为hi，高度为wi的第n+i项。当第i个由旋转后的重复项item不能进入stack，即wi≤H，hi≤H，则其相应的决策变量没有被定义，因此忽略不计，其余相应的变量均如此。因此利用（xi,yi）、wi、hi及ri即可确定ki在板材原片中的排样位置，因此方形件ki可用一个五元组表示[6]：

f表示将item分配到stack，如果第i个item被分配到第k个stack中，其中fik=1，则i∈N*，k∈B，否则为0。l和u是二进制的，它们表示两个item的相对位置lij=1（uij=1 ），i∈N*，j∈N*，i≠j，j≠i+n且i≠j+n，用于当i和j在同一个stack中使i位于j的左边。P={p1,…,pk}明确每种排样方式中所包含的i型毛坯数量aij、排列位置和顺序，确定排样方式的使用频率mj,i=1,2,…,m,j=1,2,…,m，其中mj是整型决策变量。

在满足订单需求和相关约束条件下，使得板材原片的用量尽可能少，即使板材原片利用率（零件占用面积/板材原片面积）最大，从而达到节省材料的目的。要求满足的约束条件如下：

（1）ki与kj互不重叠：

其中：（i,j）∈N*2,i≠j,j≠i+n,i≠j+n。

（2） 在板材原片的长度方向，所有零件长度之和应不大于板材原片长度L，即：

（3） 在板材原片的宽度方向，所有零件长度之和应不大于板材原片的宽度M，即：

（4） 每个item（i∈N）必须在没有重叠的情况下进行包装，并且ki必须完全包含在其分配的stack中：

（5）ki的边必须与板材原片的边平行，且在放入时可以进行90°旋转：

（6） 最终切割生成的产品项是完整的，非拼接而成：

其中：xj∈N,j=1,2,…,K。

这是一个二维三阶段剪切下料问题，求解的目标可以简述为使用数量最少的板材原片，排完全部数据集给出的所有订单毛坯[7]。通过建立混合整数规划模型确定所求的目标函数如下：

其中：z为板材原片的数量，i为毛坯型号，m为待排样的毛坯种类，aij为毛坯数量，K为排样方式的种类，xj为排样方式使用的频率且为整型决策变量。

在本文中排样优化问题的解由三阶段同质排样方式（3H） 组成，满足了题中切割时在相同栈里的产品项的宽度或长度相同约束，而3H中存在约束三阶段排样问题，即求解毛坯在原片板材上的3H排样方式所得的毛坯价值最大化，相关约束排样问题的整数规划模型表示如下：

其中：Zp表示3H排样方式最大化板材中所包含的毛坯总价值，ai表示3H中的i型毛坯的数量，vi表示i型毛坯的价值，ri表示i型毛坯的当前剩余需求量。

3 仿真实验设计与分析

3.1 仿真实验

实验环境：硬件配置为Intel 酷睿i5，主频1.80GHz，内存12GB；软件配置为Windows11 64 位操作系统；求解均使用MatlabR2018b 编程实现。在程序测试时，设定板材原片尺寸为2 440×1 220，切缝宽度为1，输入参数为：（1） 单个批次产品项总数上限max_item_num=1 000；（2） 单个批次产品项的面积总和上限max_item_area=250（m2）。为了增加实验的可信度，本文针对排样优化问题共收集了4 个数据集进行算法的验证，分别为数据集dataA1、dataA2、dataA3 和dataA4。各数据集均源于中国研究生创新实践系列大赛网站（https://cpipc.acge.org.cn），其中各个数据集是相互独立的。

3.2 模型求解与结果分析

本文运用贪婪最佳优先搜索算法对混合整数规划模型进行求解。贪婪最佳优先搜索是一种启发式搜索算法，也可以把它看成广度优先搜索算法的一种改进；算法思想是将节点按距离目标的距离进行排序，然后以这个距离为代价选择待扩展的节点[8]。在对方形件排样优化过程中，每一步都选用当下解空间的最优排放顺序，通过一次遍历就可以得到最优解。以下是程序运行出来的排样方案效果图，因数量太多，此处针对每个数据集仅列举部分图片。图2 至图5 分别为数据集dataA1、dataA2、dataA3和dataA4 的部分排样图。从图中可知，每一块板材都得到了极大地利用，浪费空间很小。

图2 dataA1 排样图

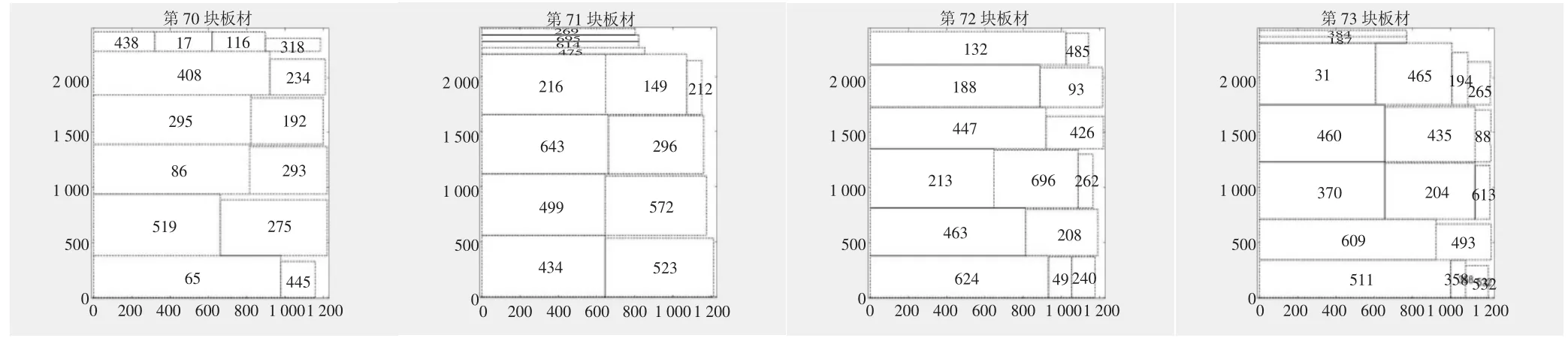
图3 dataA2 排样图

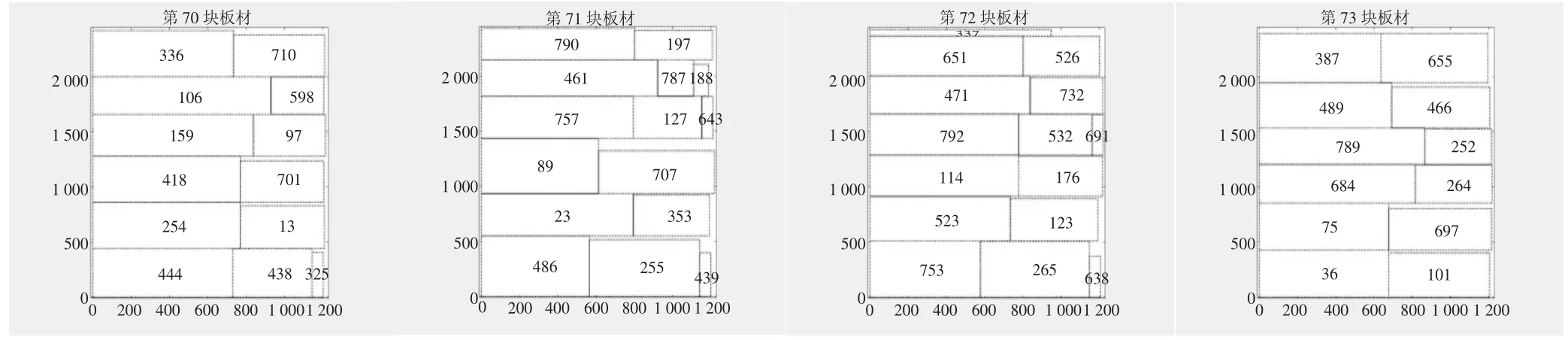
图4 dataA3 排样图

图5 dataA4 排样图

本文以板材利用率（产品项面积之和/使用原片面积之和） 作为结果指标，实验结果对比如表1 所示，板材利用率分别为91.70%、90.97%、93.97%和95.07%，说明该算法在节省板材资源和提高板材利用率方面效果显著。本文算法在dadaA1、dataA2、dataA3 和dataA4 数据集生成排样方案的过程中分别考察了90 个、90 个、88 个和85 个排样方式，平均每个排样方式耗时0.05s。由此可见该算法还具有灵活、高效和计算方便的优点。

表1 实验结果对比表

4 小 结

排样优化问题广泛地存在于产品制造企业，如3C、板式家具、玻璃、钣金件等行业的生产过程中，一个好的优化算法可解决材料利用率低、生产效率低及个性化与生产高效性之间的矛盾。针对排样优化问题，本文设计了一种基于贪婪最佳优先搜索算法生成相同栈里的产品项的宽度或长度相同的三段排样方式，减少了原材料的浪费，提高了板材利用率，为制造企业进行大规模个性化定制提供了可能。本文模型结合实际情况建立，与实际情况密切联系，通用性和推广性很强。同时实验结果表明，本文的算法可以有效地减少板材用量，且计算时间可以满足实际应用需要，具有一定的现实意义。此外订单组批问题是个性化生产模式中的另一关键问题，下一步将对此问题进行深入研究，通过订单组批来保证货物的交货期，帮助企业实现订单的批量化生产。