基于双矢量模型预测功率控制的Vienna整流器设计
2023-12-11冯兴田代站疆孙涌铭
冯兴田, 代站疆, 孙涌铭
(中国石油大学(华东)新能源学院,山东青岛 266580)
0 引 言
三相Vienna整流器具有电路结构简单,无桥臂直通风险,高功率密度,高效率和低电流谐波畸变率等优点[1-2],因此被广泛应用在电动汽车充电器、通信电源、风力发电和航空电源等领域[3-5]。
近年来,随着微处理器和数字信号处理器的快速发展,有限集模型预测控制由于其具有多目标约束,响应速度快等优点在Vienna 整流器上得到了广泛的应用[6-8]。应用于Vienna整流器的有限集模型预测控制有电流控制和功率控制两种,分别以电流误差最小和功率误差最小为控制目标。文献[9-11]中提出有限集模型预测电流控制,建立了以电流为控制目标的价值函数,选择电流跟踪精度最高的矢量并输出开关信号。文献[12]中提出有限集模型预测功率控制,建立以功率为控制目标的价值函数,通过寻优计算得到使下一时刻功率变化最小的矢量并作为最优矢量。然而上述的模型预测控制在控制周期内都只能输出单个作用矢量,矢量跟踪误差大,控制量存在较大波动。为此,文献[13]中在控制周期内引入零矢量作为第二矢量与最优矢量共同跟踪控制量,但是该方法确定的矢量组合并不是全局最优,控制性能提升有限,文献[14]中将第二矢量扩大到非零矢量,并采用求导的方法计算矢量的作用时间,但系统的运算量较大,且计算出的矢量作用时间可能不在控制周期的范围内,从而变为传统的单矢量控制降低系统的跟踪精度。
针对上述分析,为了减小Vienna整流器有限集模型预测功率控制中的功率波动,提高系统控制精度。本文提出一种双矢量模型预测功率控制策略,在控制周期中引入第二矢量与最优矢量共同作用。将有功功率准确跟踪参考值和双矢量功率跟踪误差最小作为第二矢量的选择原则,相比传统的有限集模型预测功率控制策略能够有效提高功率的跟踪精度,减小输入电流的谐波畸变率。同时设计并搭建基于DSpace 的Vienna整流器实验平台,验证所提出控制策略的有效性。
1 三相Vienna整流器的数学模型
三相Vienna整流器的拓扑结构由6 个整流二极管D1~D6和3 个双向开关单元Sa、Sb、Sc所构成,如图1 所示。Vienna整流器的交流侧连接电网,ea、eb、ec为三相交流电压,ia、ib、ic为三相输入电流。L为交流侧滤波电感,R为交流侧输入电阻。整流器的直流侧接入负载RL,直流侧输出电压为udc,C1、C2为直流侧的上下滤波电容,其电容值均为C。
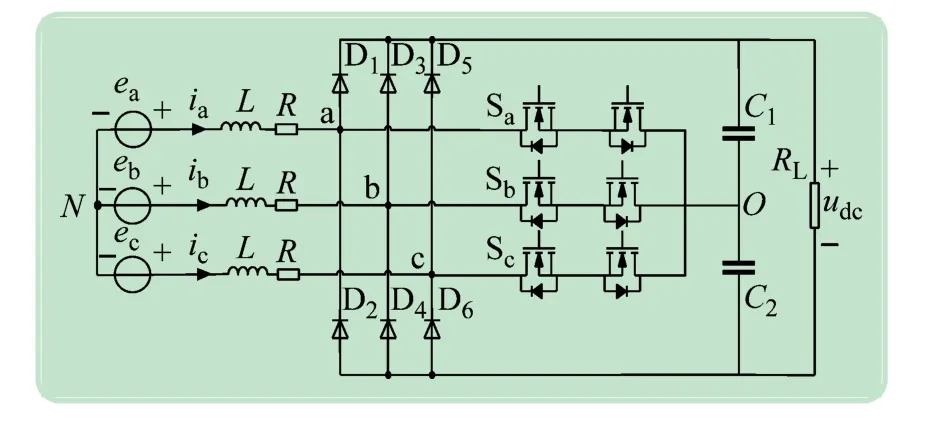
图1 三相Vienna整流器主电路结构
根据图1 所示的Vienna整流器主电路结构,可以推导出Vienna 整流器在三相静止坐标系下的数学模型为:
式中:u(a,b,c)N为整流桥交流输入端与三相交流电源中点N之间的电压;uNO为三相交流电源中点N与直流侧电容中点O之间的电压;Shp、Shn(h分别代表a,b,c)分别为直输出侧正向电流和负向电流的开关函数;uc1、uc2分别为直流侧上下电容电压。
为了进一步对控制策略进行分析,利用Clarke 变换将三相静止坐标系下的数学模型变换到两相静止的α、β坐标系下有:
式中:eαβ、iαβ分别为交流侧输入电压和交流侧输入电流的α、β轴分量;uαβ为在α、β坐标系下整流器交流侧输出电压;Sαp(n)、Sβp(n)为在α、β坐标系下的开关函数。
2 传统的有限集模型预测控制
Vienna 整流器的传统有限集模型预测功率控制首先建立功率预测模型和功率误差价值函数;其次将备选矢量带入功率预测模型中得到k+1 时刻的功率预测值;最后将计算出的功率预测值带入功率误差价值函数中找到使功率误差价值函数最小的预测值,并得到对应的最优矢量Vm。对式(2)进行离散化,可得:
式中:Ts为采样周期其远远小于电网电压周期;k为在kTs时刻,k+1 表示在(k+1)Ts时刻。
根据瞬时功率理论可以计算出系统的瞬时有功功率P和瞬时无功功率Q,即:
对式(4)进行微分运算得到P和Q在t时刻的变化量:
根据t=kTs时刻的采样值,计算得到该时刻的瞬时P和瞬时Q,忽略输入电阻R可以预测出t=(k+1)Ts时刻的瞬时P(k+1)和瞬时Q(k+1)为:
将式(5)代入式(6),得到:
式中,ω为电网电压角频率。为了控制Vienna 整流器系统运行时的功率,以P、Q误差的平方和为指标构造价值函数:
有功功率参考值Pref通过功率外环得到,无功功率参考值Qref一般设置为0。将备选矢量集代入价值函数中进行寻优即可得到最优矢量。
3 双矢量控制策略
应用于Vienna 整流器的传统有限集模型预测功率控制策略,在每一个扇区中只有7 个有效矢量参与寻优计算,且在一个控制周期中只能够输出单个作用矢量,功率跟踪精度低,输入电流质量差。为了获得较好的控制效果往往需要较大的滤波电感或者更高的采样频率。为了解决这一问题,本文将控制周期划分为2个区间,引入第二矢量Vn和最优矢量Vm共同作用,通过分配Vm和Vn的作用时间提高对功率的跟踪精度。图2 为所提出双矢量控制策略下有功功率斜率的变化示意图,图中fpr(r分别代表l,m,y,n,z,o,q)为控制周期内矢量作用时P的斜率。

图2 双矢量控制策略下的有功功率斜率变化关系
在一个控制周期中,假设作用矢量对功率的影响保持不变,则在控制周期结束时P和Q可以表示为:
式中:fpm和fpn分别为Vm和Vn作用时P的斜率;fqm和fqn分别为Vm和Vn作用时Q的斜率;tm为Vm的作用时间;tn为Vn的作用时间。结合式(3)~(5)可得:
式中,x分别代表m、n。
为了确保双矢量控制有较高的跟踪精度,本文首先通过价值函数判断出Vm,再根据最优矢量作用时fpm的符号,在备选矢量集中选择使有功功率准确跟踪参考值并且使双矢量功率跟踪误差最小的矢量作为第二矢量。由图2 可见,根据P准确跟踪参考值原则有
由此可计算出2 个矢量的作用时间为:
根据式(11)、(12)在每一个控制周期中都可以实现对P的零误差跟踪,则双矢量控制策略下的功率跟踪误差即为Q的跟踪误差为
根据式(12)、(13)和双矢量功率跟踪误差最小原则,即可得到Vn,所提出Vienna 整流器双矢量模型预测功率控制策略框图如图3 所示。
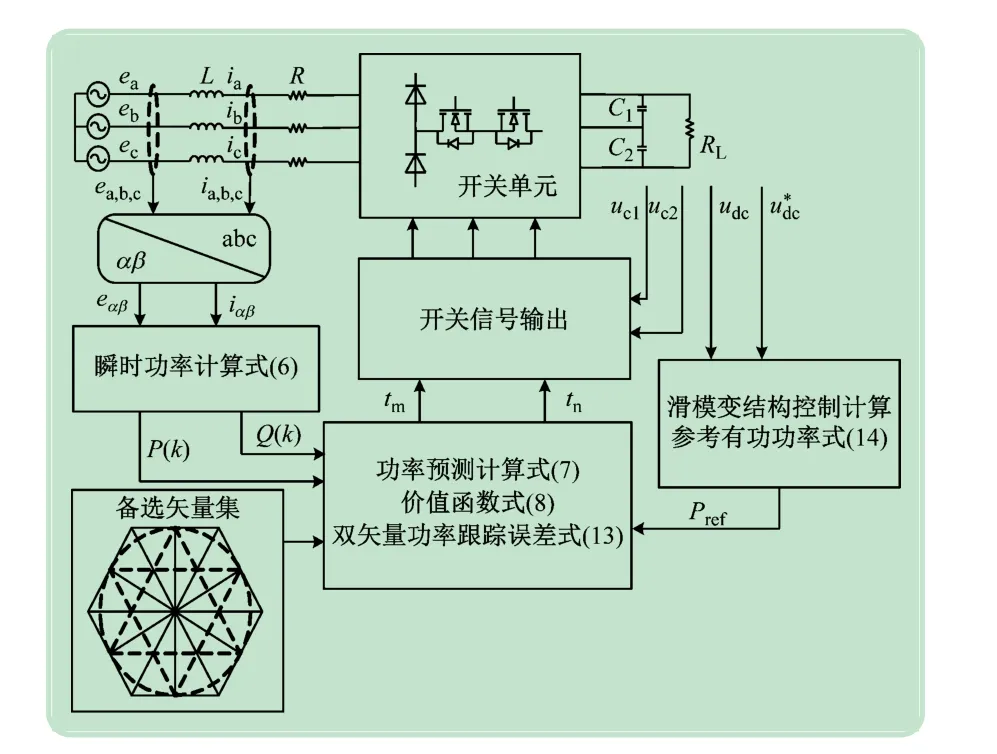
图3 Vienna整流器双矢量模型预测功率控制策略框图
在所提出的控制策略中功率外环采用滑模变结构控制,忽略线路损耗,根据文献[15]中的方法可得P参考值为
式中:C为直流侧电容值;M为控制系数;为输出电压的参考值。
4 系统仿真与实验分析
4.1 仿真分析
为了验证所提出控制策略的有效性,在Matlab/Simulink中建立仿真模型,验证分析所提出控制方法的性能。系统仿真模型参数:输入线电压为380 V;输入电阻R=0.4 Ω;滤波电感L=3 mH;输出电压udc=650 V;直流侧电容C=3.3 mF;采样频率fs=10 kHz。
图4 所示为采用本文所提出的双矢量模型预测功率控制策略在额定负载下的有功功率、无功功率、输入电流及其谐波分析的仿真结果。由图4 可见,本文提出的控制方法能够对功率进行准确的跟踪,有功功率和无功功率的脉动较小,且都能在参考值附近稳定。经过谐波分析可知在稳态情况下所提出控制方法的输入电流谐波畸变率为1.82%。

图4 双矢量模型预测控制策略仿真分析
图5 所示为传统控制方法在额定负载下有功功率、无功功率、输入电流及其谐波分析的仿真结果,其中Mag为相对基波幅值。对比图4、图5 可以看出,与本文所提出的控制策略相比,传统控制方法在控制周期内输出的单个作用矢量对功率的跟踪效果较差,有功功率和无功功率均存在较大的波动,通过谐波分析可知此时输入电流的谐波畸变率为3.29%。

图5 传统有限集模型预测控制策略的仿真分析
4.2 实验验证
为了验证所提出控制策略的有效性,设计了Vienna整流器主电路,搭建了基于DSpace 的实验平台,如图6 所示。实验平台系统主要由DSpace主机与控制器、Vienna 整流器开发板、示波器、上位机、负载等组成。

图6 Vienna整流器实验平台
图7 所示为采用传统有限集模型预测方法测得的稳态波形,由图可见,虽然直流侧的电压能够在设定值上保持稳定,但是输入电流的畸变较大,在控制周期内输出的单个作用矢量难以对控制量进行精准的跟踪。
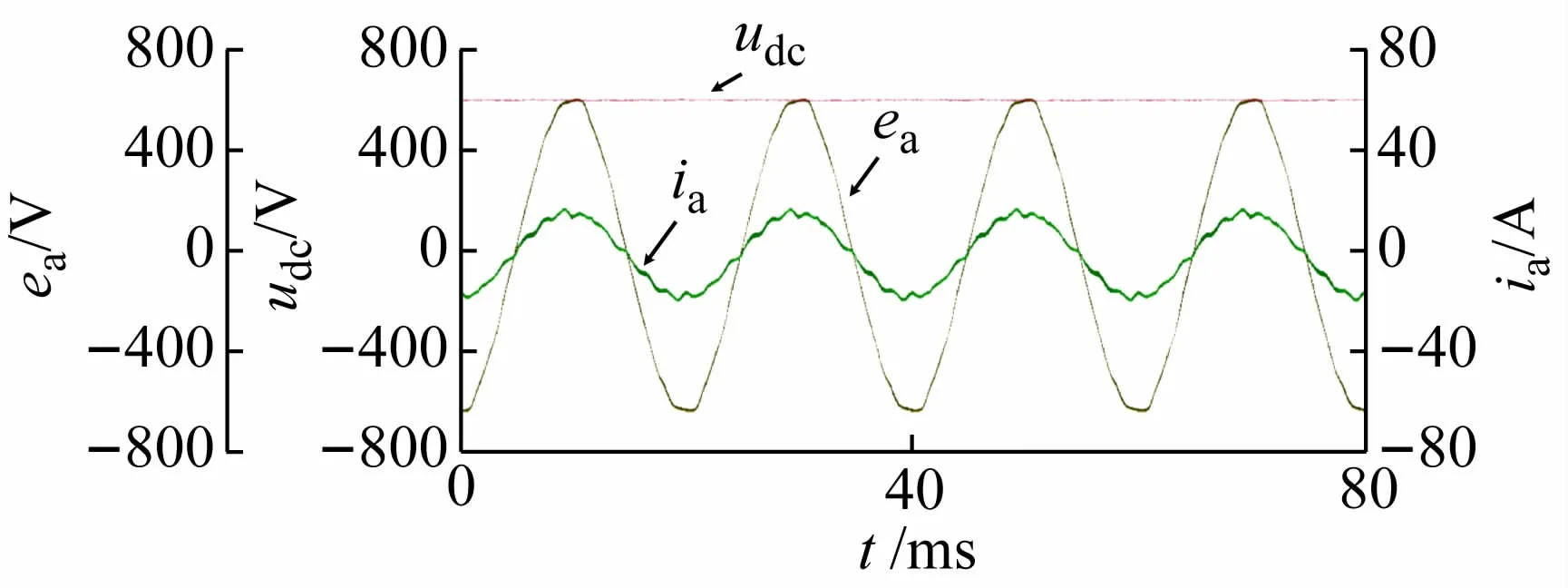
图7 传统有限集模型预测控制策略实验波形
图8 所示为采用本文所提出的双矢量控制策略测得的稳态波形,由图可见直流侧的输出电压稳定,相比于图7,输入电流质量有了明显改善,表明本文所提出的控制策略与传统控制方法相比具有较高的跟踪精度。
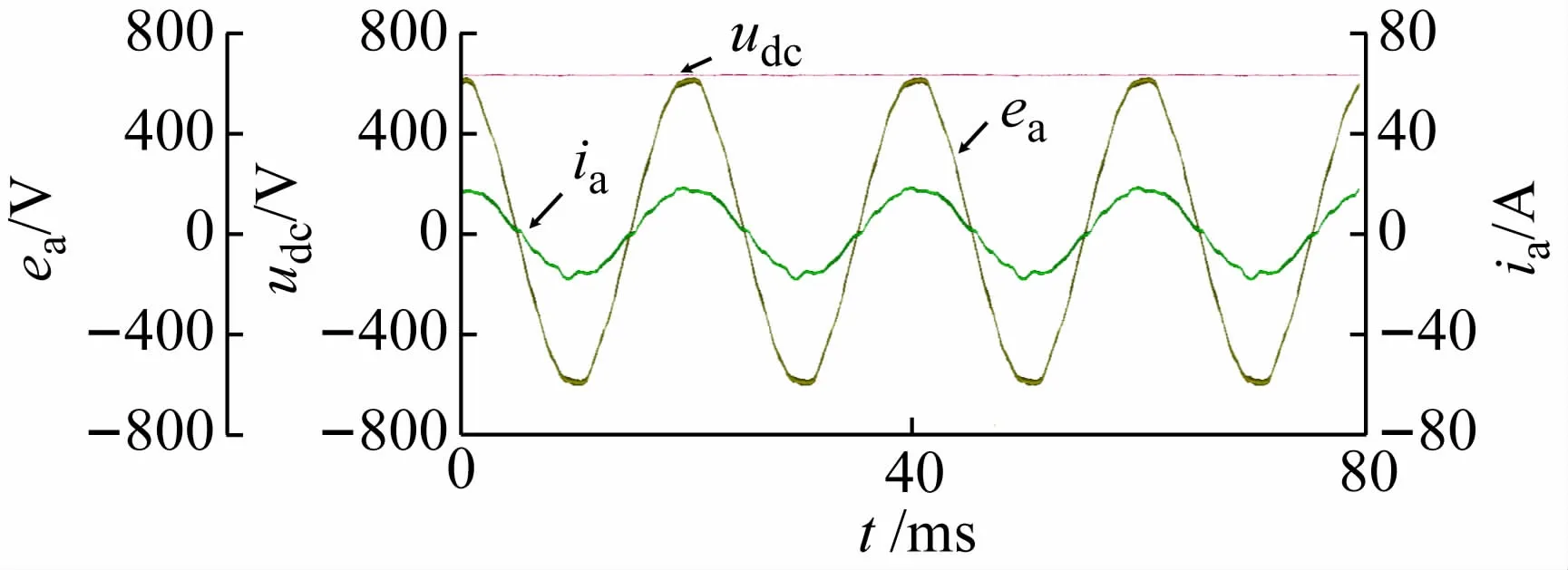
图8 双矢量模型预测控制策略实验波形
5 结 语
本文设计并搭建了基于双矢量模型预测功率控制的Vienna整流器实验平台,并通过仿真分析和实验验证了所提控制策略的可行性,结果表明:
(1)所提出的双矢量模型预测功率控制策略与传统的有限集模型预测控制策略相比,能够有效提高控制系统的跟踪精度,减小输入电流的总谐波畸变率,具有较高的功率因数。
(2)所提出的双矢量模型预测功率控制的功率脉动小,系统稳定性高,具有一定的实际应用能力。
