把握本质，注重关联

摘 要：传统小学数学教学存在诸多问题，如点状化教学、狭窄化教学、平均化教学等。在传统教学模式下，学生往往将注意力集中在某一知识点上，而忽视了知识点背后的数学思想方法、文化精神，未能建构起完善的知识结构，导致数学学习效果不佳。为了解决这些问题，教师尝试实施结构化教学，在改进传统教学模式的同时，引导学生建构知识结构，发展多样能力，增强数学学习效果。文章根据教师的现有经验，从单元整体结构、立体关联结构和本质意义结构这三方面入手，阐述小学数学结构化教学策略。

关键词：小学数学；结构化教学；教学策略

作者简介：夏梦月（1989—），女，江苏省苏州高新区通安中心小学校。

《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）明确指出，数学教学要关注知识点之间的联系，注重引导学生建构知识结构，提升知识理解水平。然而，当前的小学数学教学存在点状化教学、狭窄化教学和平均化教学等问题。其中，点状化教学表现为：教师以点状知识为重点，着重引导学生关注某一知识点，忽视知识点之间的关联。狭窄化教学表现为：教师过度关注数学知识，忽视数学知识背后的数学思想方法和文化精神。平均化教学表现为：教师对各个知识点平均用力，导致核心知识和结构知识用力不足。为了解决这些问题，教师可尝试实施结构化教学。结构化教学是以学科知识结构为基础，以学生已有经验为依据，借助单元整体结构、立体关联结构等，引导学生体验结构化活动，促使其发挥自主性，发现学科核心概念、学科分解概念等内容之间的联系，把握知识本质，建构知识结构的活动^［1］。现有实践表明，有效实施结构化教学，可以使学生把握知识点之间的关联，掌握数学思想方法，感知文化精神，建构知识结构，同时发展多样能力，如迁移应用能力、问题解决能力等，便于提升学习水平。因此，教师应当依据不同类型的结构，结合教学内容，着力实施数学结构化教学。

一、聚焦知识点之间的联系，架构单元整体结构

结构化教学关注知识点之间的联系。知识点之间的联系，是学生建构知识结构的依据。同时，《课程标准》要求教师把握知识联系，整合教学内容，实施单元教学。单元整体结构，正是单元教学的基础。有效的单元整体结构，可以使学生集中梳理知识点，发现知识点之间的联系，由此将碎片化的知识连成线、网、块、体，顺其自然地建构出知识结构，扎实掌握知识^［2］。对此，在实施数学结构化教学时，教师应当聚焦知识点之间的联系，打破单元限制，架构单元整体结构，助力学生进行结构化学习。

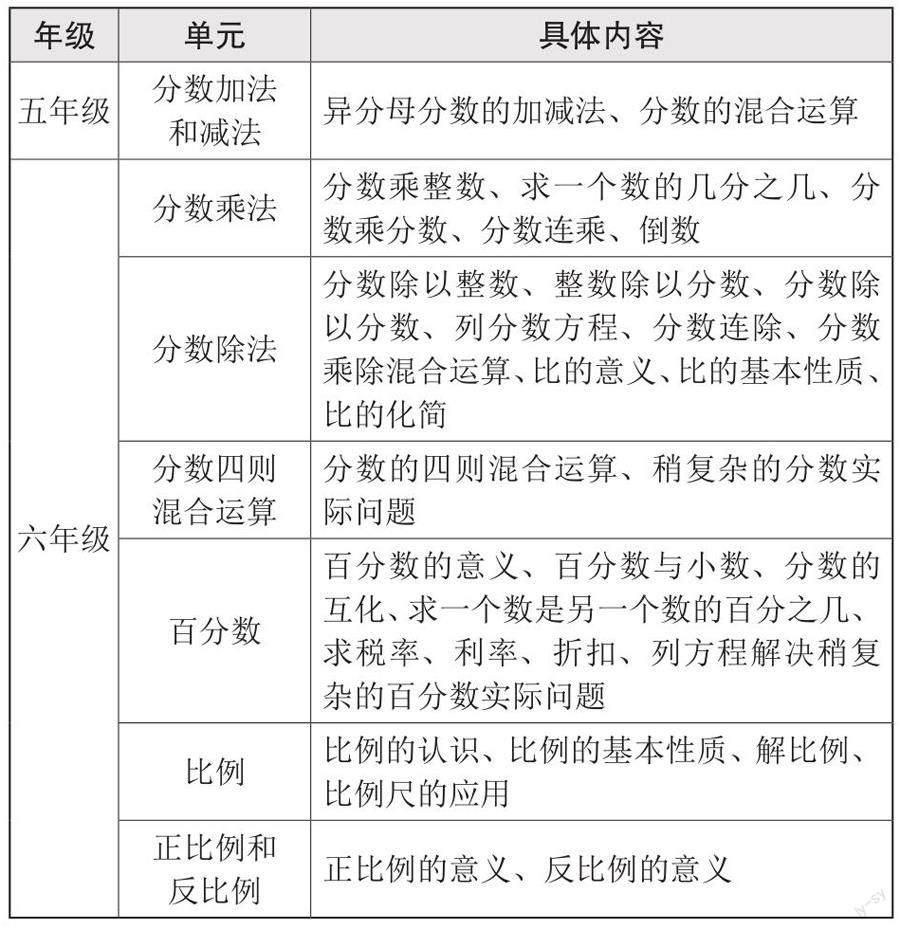
以“分数的意义和性质”为例，该单元内容主要有：約分、通分、分数大小比较、求一个数是另外一个数的几分之几、真分数与假分数、将假分数化成整数或带分数、分数与小数的互化等。该单元内容起着承上启下作用。在该单元之前、之后，教材设置了不同的“分数”内容，如表1所示。

由此可见，教材按照螺旋式上升的方式，编排了分数的相关内容。同时，这些内容有着密切联系。例如，学生在认识了分数后，方可进行分数加、减、乘、除运算。所以，通过梳理教材内容，教师发现了知识点之间的联系，并以此为基础，重新整合相关内容，建构单元整体结构，就此引导学生进行整体学习，了解每个知识点及其关系，形成知识结构，实现知识点之间的融会贯通。

二、紧扣知识关联，建构立体关联结构

结构化教学注重知识全貌。知识关联是学生了解知识全貌的基础^［3］。具体来说，通过把握知识关联，学生可以建构出立体的关联结构，由此整体地认知知识全貌，加深对知识的理解。因此，在实施数学结构化教学时，教师应在建立单元整体结构的基础上，以具体的教学内容为依据，引导学生经历知识形成过程，把握知识关联，建构立体关联结构。

（一）经历知识形成过程，把握知识点内部元素的关联

数学知识点具有复杂性。大部分知识点内部有不同的元素。而且，不同元素之间有着密切的联系，共同组成知识点。所以，学生要想深刻地认知知识点，需要把握元素之间的联系。通过把握元素之间的联系，学生可以立体化地认知知识点，为建构知识结构奠定坚实基础。对此，在数学课堂上，教师应以知识点内部元素为着眼点，组织相关活动，引导学生体验、经历知识形成过程，由此把握元素之间的联系，立体化地理解知识点。

以“圆的认识”为例，圆是本节课重要的知识点。在学习该知识点的过程中，学生需要了解圆心、直径、半径、对称轴。这些内容正是圆的内部元素。同时，这些元素之间有着密切联系，缺一不可，共同构成圆。为使学生感受到这些元素之间的联系，教师分层组织活动。首先，教师提出操作任务：“请大家在纸张上随意地画出三个大小不同的圆。”在此任务的驱动下，学生迁移已有认知，认真操作，得到三个大小不同的圆。实际上，在绘制圆的过程中，学生进一步增强了认知。

接着，教师继续提出任务：“请大家将这三个圆剪下来，试着折一折、比一比，看看有什么发现。”在此任务的作用下，学生继续动手操作。在此次操作的过程中，学生手脑结合，审视“现象”，有所发现，如：“当折一个圆时，其中会出现很多条线段，这些线段的长度是一样的。”“在折不同的圆时，圆内的线段长度不同。”“圆内的所有线段都相交于一点。”教师对此进行赞赏，并向学生发问：“圆中的这些线段是什么？所有线段相交的点是什么？”受到问题的驱使，一些学生走进数学教材中，探寻相关的数学内容，试着用数学的语言进行描述，如：“所有线段交汇的点是圆心。”“穿过交汇点的线段是直径。”立足学生的描述情况，教师及时地进行总结，促使其建构正确认知。

最后，教师再次向学生追问：“圆的直径有多少条？这些直径之间有怎样的关系？”“直径的一半是什么？有什么特点？”学生带着问题，细心回顾操作过程，审视操作结果，透过直观现象，获取问题答案，由此掌握数学知识。

由此可见，通过体验活动，学生经历了数学知识形成过程。在此过程中，学生发挥自主性，积极操作、思考，与直观的数学现象互动，逐步发现圆心、直径和半径，了解其特点，由此立体化地认知了圆，建构了知识结构，提高了数学知识理解效果。同时，不少学生也因此锻炼了操作能力、思维能力、抽象能力等，从而提升了数学学习水平。

（二）经历知识形成过程，把握知识点之间的关联

知识点之间的关联，是学生建构关联结构的关键^［4］。建构主义学习理论指出，迁移应用已有认知，是学习者实现有意义建构的重中之重。简单来说，学生迁移应用所学知识解决问题，可以顺其自然地发现知识点之间的关联，由此建构关联结构。所以，在实施数学结构化教学时，教师应以单元整体结构为基础，以知识点之间的关联为立足点，以学生学习情况为依据，引导学生经历知识形成过程，迁移应用所学知识，借此把握知识点之间的关联。

以“梯形的面积”为例，在本节课之前，学生学习了长方形、正方形、平行四边形、三角形等平面图形的面积计算公式。在学习的过程中，学生体验操作活动，获取了诸多方法，尤其掌握了数学思想方法——转化法。立足于学生的学习情况，在课堂上，教师直接组织小组探究活动。具体来说，教师向学生提出合作探究任务：“请大家回顾之前所学的平面图形面积计算公式。我们是如何推导出它们的面积计算公式的？在推导的过程中，使用了哪些方法？是否可以使用这些方法推导梯形的面积计算公式？请大家先自主思考这些问题，接着与小组成员交流，确定推导梯形面积计算公式的方法，并试着实践这些方法。”在提出任务后，教师给予学生充足的合作探究时间。

在进行合作探究时，学生在具体任务的驱动下进行头脑风暴，回顾所学知识，联想不同的方法，继而与小组成员一起交流。在交流的过程中，不同的组员提出了不同的方法。面对诸多方法，学生兴致高昂，纷纷动手操作。例如，有学生沿着梯形的一条高进行剪切，并将剪下的三角形摆放到斜边处，得到一个长方形；有学生沿着梯形上底和下底的中线进行剪切，并将两个部分沿着斜边进行拼接，得到一个长方形。在如此操作的过程中，学生细心观察，发现梯形与长方形的关系，继而迁移已有认知，试着用长方形的面积计算公式推导出梯形的面积计算公式。也有学生用两个完全相同的梯形拼成一个平行四边形，观察原来的梯形和拼成的平行四边形之间的关系，继而推导出梯形的面积计算公式。

实践表明，通过体验如此活动，学生经历了数学知识的形成过程。在此过程中，学生发挥自主性，迁移已有认知，利用数学思想方法、数学知识解决问题，获取新知，同时强化数学思想方法，并以此为“桥梁”，建构知识联系，形成立体的知识结构，增强结构化学习效果。

三、依据知识本质，构筑本质意义结构

结构化教学的目的之一是使学生掌握知识本质内涵。从数学知识点到知识本质的过程，其实是学科结构到学生认知結构的过程^［5］。此过程不是自然而然产生的，需要有一个载体，即多元表征。在进行多元表征时，学生会利用多元的方式，对数学知识进行编码、转译等，由此逐步发现知识本质，构筑出本质意义结构。由此，在实施数学结构化教学时，教师应以知识本质为重点，引导学生进行多元表征，借此使其把握知识本质，构筑本质意义结构。

由此可见，学生体验直观表征、数学建模活动，经历了数学知识的形成过程。在此过程中，学生一步步地感知知识本质，形成意义认同，有利于构筑意义结构，继而灵活应用，解决数学问题。

总之，有效实施结构化教学，可以使学生体验多样活动，建构单元整体结构、立体关联结构、本质意义结构，提升数学理解水平，提高数学学习效果。鉴于此，在《课程标准》的指引下，教师要审视传统教学的不足，并以此为基础，实施结构化教学，立足教学内容，以单元整体结构、立体关联结构和本质意义结构为基础，应用适宜的策略，引导学生体验、探究、把握知识之间的联系，建构整体认知，由此增强数学学习效果。

［参考文献］

［1］钟雪春.浅析如何实施小学数学结构化教学策略［J］.考试周刊，2022（9）：102-105.

［2］王哲燕，段安阳.小学数学“结构化”单元整体教学的理解与实践［J］.教育科学论坛，2022（5）：22-25.

［3］马少清.关于小学数学结构化教学的几点思考［J］.小学教学参考，2021（29）：86-87.

［4］江帼英.小学数学结构化教学实施策略分析［J］.教育界，2021（24）：61-62.

［5］唐伟.小学数学结构化教学实践分析［J］.数学大世界（上旬），2021（4）：32.