双圆弧谐波传动齿廓修形及啮合特性分析
2023-12-11杜雅宁王士军郑苏芮
杜雅宁 王士军 齐 娜 王 程 郑苏芮
(山东理工大学机械工程学院,山东 淄博 255000)
谐波传动因其体积小、传动精度高、承载能力强等特点,被广泛应用于航空航天、工业机器人、精密机床等多个领域[1-2]。谐波传动主要依靠柔轮在波发生器的作用下产生周期性的波动变形与刚轮进行啮合运动来实现运动的传递[3],柔轮在与刚轮的啮合运动过程中极易发生啮合干涉导致柔轮发生应力集中、轮齿磨损等现象,因此柔轮齿与刚轮齿间的无干涉啮合是研究的重点。张立勇等[4]根据谐波传动的包络理论,分析了谐波传动径向变形量对啮合特性的影响,并通过有限元法进行验证。张宁等[5]发现柔轮在装配后实际齿廓线空间位置与理论位置不符,提出了一种轮齿齿廓线的修正方法。李鹏超等[6]通过线性法调整柔轮齿的轴向齿高,使柔轮齿与刚轮齿不发生啮合干涉。但在实际工作工程中,由于柔轮齿圈的存在,使得柔轮沿轴向的径向变形量呈非线性关系,导致线性法设计修形存在一定偏差,不满足实际的传动要求。
本文以无公切线双圆弧齿廓为研究对象,采用改进运动学法求解出共轭刚轮齿廓。为消除柔轮在不同径向变形量下与刚轮啮合产生的干涉,基于有限元径向变形量结合轮齿修形理论,对柔轮齿廓进行三维修形,并对比分析了线性修形法与有限元修形法修形后的柔轮等效应力分布情况。
1 双圆弧谐波传动共轭齿廓设计
1.1 柔轮轮齿双圆弧齿廓设计
谐波传动中,双圆弧齿廓具有更大的包络存在区间。本文研究采用无公切线双圆弧齿廓,相较于公切线双圆弧齿廓,其共轭存在区间较大且设计求解过程更加简单,便于加工生产,其基本齿形如图1 所示,图1 中各参数的意义见表1。
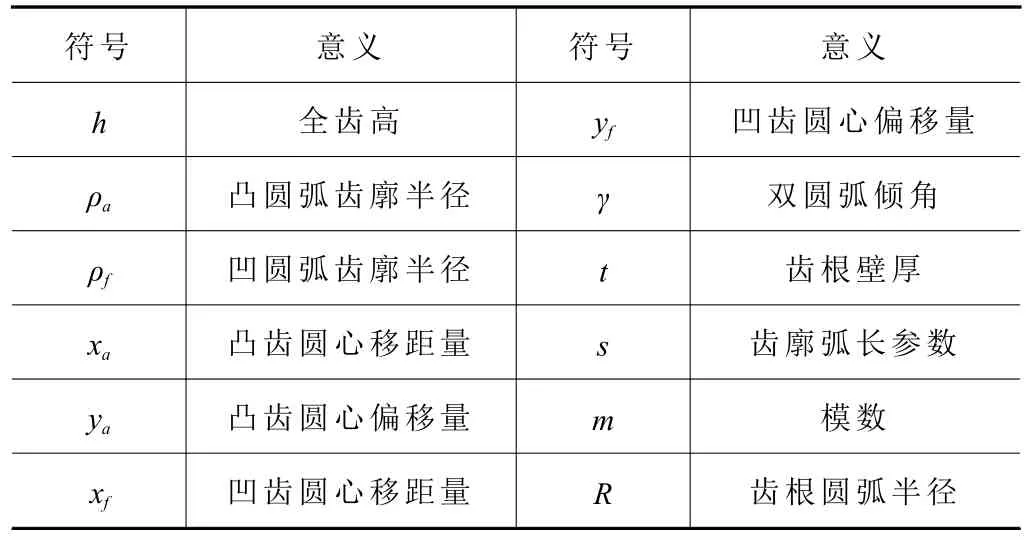
表1 双圆弧齿廓参数及意义
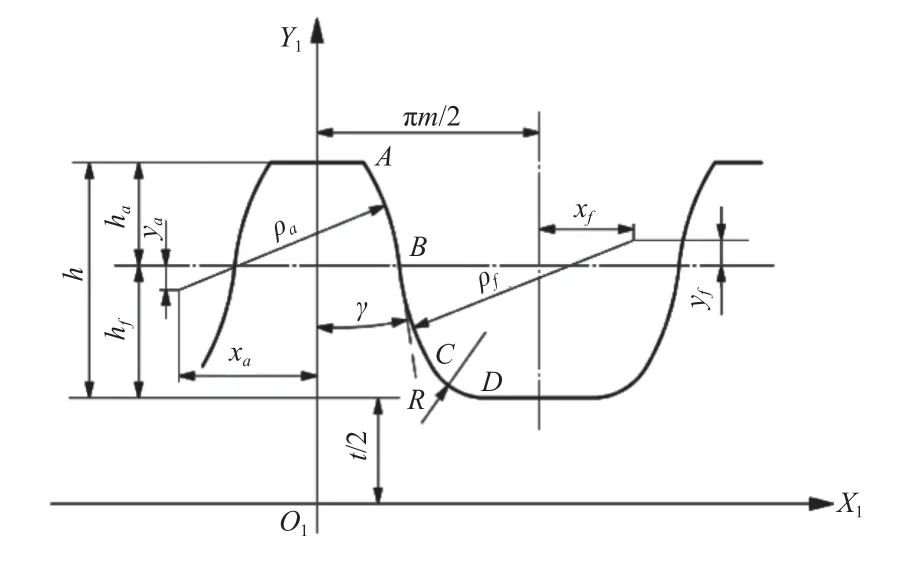
图1 无公切线双圆弧齿廓坐标系
将柔轮轮齿的对称轴定义为Y1轴,将Y1轴与柔轮中性层曲线的交点定义为坐标原点O1,过原点O1作中性面的切线,切线定义为X1轴,建立柔轮轮齿局部动坐标系{O1,X1,Y1}。
双圆弧齿廓由凸圆弧AB、凹圆弧BC以及过渡圆弧CD组成。以从齿顶A处起的弧长s为参数,r为右侧齿廓的失径,n为其对应的法向量。
凸圆弧齿廓AB段为
凹圆弧齿廓BC段为
将分段函数的弧长s离散为n个点,采用改进运动学法[7-8]求解不同弧长s对应的共轭转角φli(i=1,2,···,n),通过谐波传动精确转角关系将式(1)与式(3)进行坐标变换,再将φli代入到变换后的公式中即可以求得离散的刚轮齿廓数值坐标点集合,最后通过最小二乘法拟合得到特定的刚轮实际齿廓。
1.2 双圆弧柔轮齿廓修形原理
假设柔轮内壁与波发生器的接触状态为线接触,在波发生器装入柔轮后,柔轮轮齿在柔轮筒底和波发生器的影响下会产生弹性变形和法向倾角,柔轮齿在波发生器长轴附近会向外张开一定角度,在短轴处会向内收缩一定角度,柔轮齿沿轴向方向发生不同程度的径向变形。变形示意图如图2 所示。

图2 柔轮变状态图
根据理论线性变形原理[9]可以求得在柔轮轴向上距筒底为Zg的任意截面的理论径向变形量为
式中:ω0为柔轮主截面最大径向变形量;Z0为主截面到柔轮筒底的距离。
在实际工作中,由于柔轮内壁与波发生器接触状态复杂以及柔轮齿圈的影响,导致线性计算的径向变形量不满足使用要求,故需要通过有限元法计算柔轮长短轴实际径向变形量。
通过改进运动学啮合理论与Matlab 参数化编程,在不改变任意截面齿廓形状的条件下,合理调整柔轮齿根壁厚,使柔轮齿廓在任意转角下都位于刚轮齿槽内,从而实现无干涉啮合。线性法修形是根据柔轮壁厚的调整量与齿宽的线性关系,确定其余各截面的壁厚调整量的。有限元法修形是根据各截面的径向变形量与轮齿间的啮合状态来确定壁厚调整量的。
线性法修形后与有限元法修形后的柔轮齿形如图3 所示,图中dq与dh分别为前端修形量与后端修形量,虚线为修行前的柔轮齿,实线为修形后的柔轮齿。
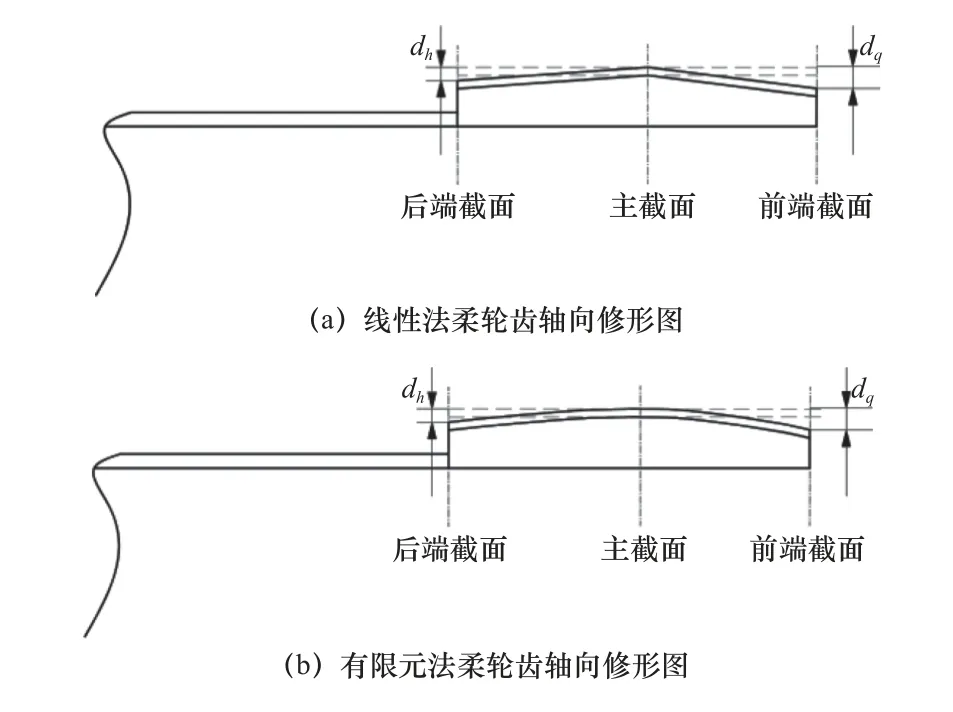
图3 柔轮轮齿轴向修形图
2 谐波传动的有限元分析
2.1 共轭空间齿廓计算实例
以模数m=0.4、柔轮齿数z1=160、刚轮齿数z2=162、径向变形量ω0=0.42、刚轮固定、余弦波发生器作为输入、柔轮作为输出、传动比i=80 的无公切线双圆弧谐波减速器为研究对象,采用改进运动学法计算出柔轮齿廓和共轭刚轮齿廓参数,结果见表2 和表3。
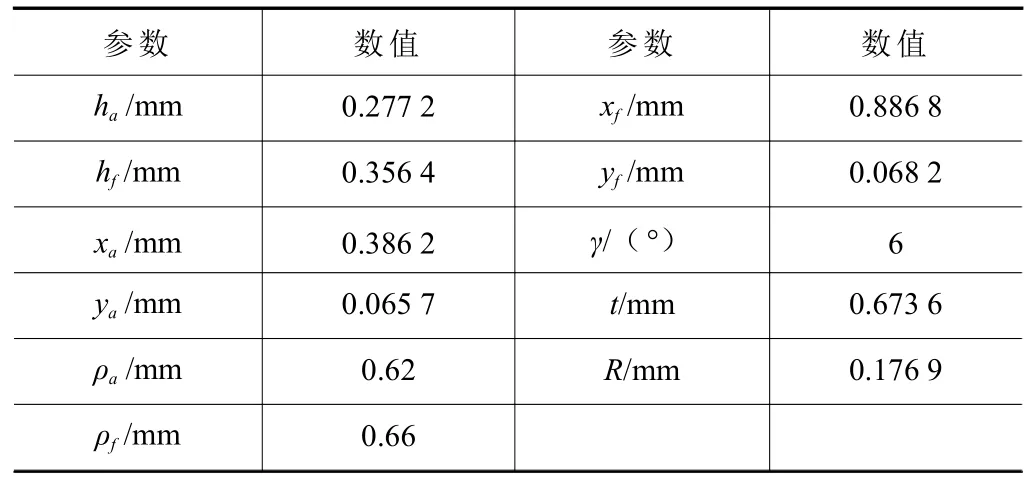
表2 柔轮齿廓参数
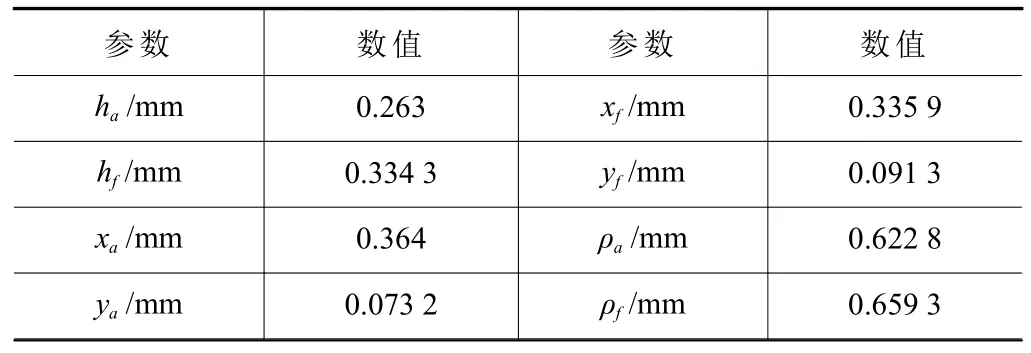
表3 刚轮齿廓参数
2.2 仿真实体建模
在SolidWorks 中建立谐波减速器三维模型,此时柔轮轮齿在轴向为平齿,未修形。谐波减速器的波发生器由凸轮和柔性轴承组成,在有限元分析中可将凸轮与轴承进行一体化建模[10]。建模过程中从短轴处将凸轮对称分为两部分,并施加位移约束,约束方向与凸轮长轴方向一致,约束大小为柔轮径向变形量0.42 mm,这样做可以避免装配过程中柔轮与波发生器产生干涉。将模型导入到Ansys Workbench 进行分析,具体分析过程如下。
(1)材料选取。谐波减速器中柔轮材料选用30CrMnSiA(密度为7 750 kg/m3,弹性模量为204 GPa,泊松比为0.29);刚轮和余弦凸轮材料选用45#优质碳素结构钢(密度为7 850 kg/m3,弹性模量为210 GPa,泊松比为0.269)。
(2)接触设计与网格划分。波发生器与柔轮,柔轮齿与刚轮齿间的接触方式为面与面的摩擦接触,波发生器外表面、刚轮轮齿表面为目标面(Target),柔轮齿圈内表面与轮齿表面为接触面(Contact),摩擦系数设定为0.2,法向刚度因数设定为0.1,采用八节点六面体单元对模型进行网格划分[11]。
(3)设置约束及载荷。有限元分析步骤设定为3。第1 步对分割后的波发生器施加位移约束,使波发生器恢复处理前的形状,模拟波发生器的装配;第2 步对刚轮设置位移约束,使刚轮从后端装入柔轮,刚轮齿廓与柔轮齿廓接触;第3 步释放柔轮绕轴向的旋转约束并对柔轮输出端施加额定扭矩T,T=60 N·m。
2.3 柔轮变形分析
通过Ansys Workbench 进行三维实体有限元分析,得到柔轮径向位移分布云图,如图4 所示。
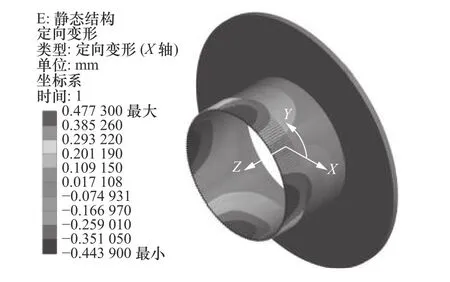
图4 柔轮径向位移分布云图
提取图4 中截面1(前端截面)、截面2(主截面)、截面3(后端截面)中性层最大径向变形量见表4。表中理论径向变形量由式(5)计算而得。
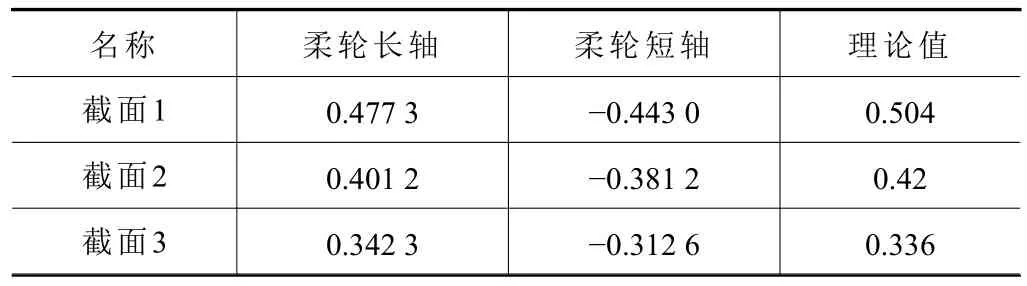
表4 柔轮各截面中性层最大径向变形量 mm
由表4 可知,柔轮中性层长短轴实际径向变形量与理论值相差较大,前端截面和主截面柔轮最大径向变形量小于理论值,而在后端截面柔轮最大径向变形量大于理论值,故线性修形不满足实际要求,需采用有限元法对柔轮齿廓进行修形。
将有限元仿真结果带入Matlab 仿真程序中,可得到单个柔轮轮齿相对固定刚轮齿槽的运动轨迹,如图5 所示,柔轮齿与刚轮齿在前端截面整体产生干涉,在主截面和后端截面柔轮齿与刚轮齿在啮合区产生干涉。

图5 未修形时柔轮齿运动轨迹
3 柔轮有限元法齿廓修形
柔轮有限元法修形的具体方法是利用有限元分析得到的柔轮轮齿轴向各截面的径向变形量结合Matlab 参数化编程,观察单个柔轮齿与刚轮齿的运动轨迹,根据轮齿间的干涉情况,调整各截面柔轮齿根壁厚,使刚轮齿与柔轮齿无干涉啮合。
图6 所示为线性修形法与有限元修形法的修形量对比图,对有限元法的修形量进行多项式拟合得到修形量方程:

图6 柔轮齿修形量对比图
式中:h为壁厚修形量,b为各截面距后端截面3的距离。修形后各截面运动轨迹如图7 所示,有限元法修形后各截面柔轮齿与刚轮齿均可实现无干涉啮合。
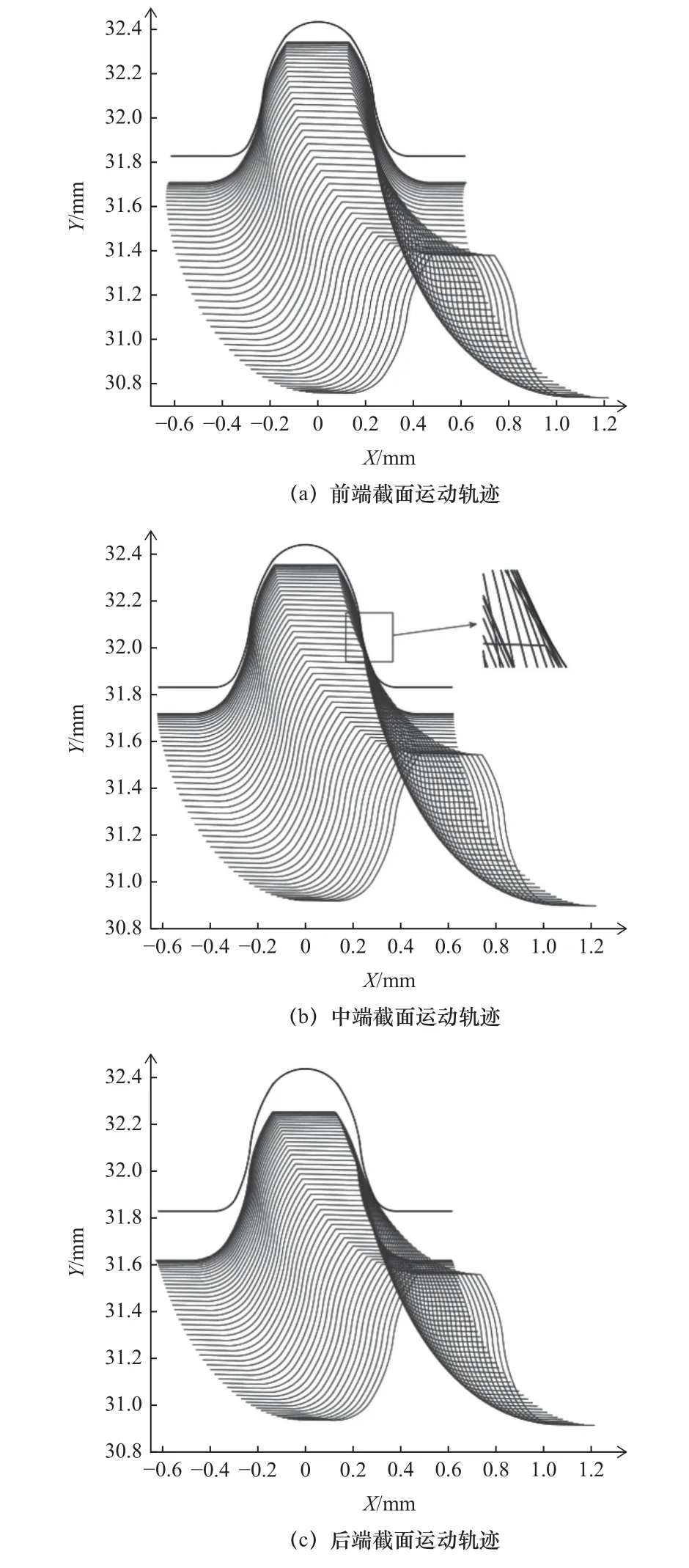
图7 修形后柔轮各截面啮合轨迹
通过Ansys Workbench 分别对未修形、线性法修形、有限元法修形后的仿真模型进行有限元分析,柔轮在不同修形法下的应力云图如图8 所示。由图8可知,未修形时柔轮最大等效应力为592.6 MPa,柔轮齿前端和后端产生了应力集中的现象。线性法修形后柔轮最大等效应力为404.09 MPa,有限元法修形后柔轮最大等效应力为344.89 MPa,有限元法修形后柔轮最大等效应力主要集中在柔轮齿中间截面附近,且应力沿圆周方向分布更加均匀。

图8 不同修形法修形后柔轮等效应力云图
4 结语
本文基于装配变形与改进运动学理论,对谐波传动无公切线双圆弧齿廓进行了设计和修形,并对实体模型进行有限元仿真,分析了柔轮的变形及应力分布情况,得到以下结论:
(1)柔轮在实际工作过程中柔轮径向变形量与理论变形量有较大的差异,在齿圈前端柔轮最大径向变形量小于理论值,而在齿圈后端柔轮最大径向变形量大于理论值。
(2)通过有限元法修形后柔轮齿廓与刚轮齿廓在各截面均可实现无干涉啮合。
(3)未修形时柔轮齿圈处最大等效应力集中在柔轮齿圈前端位置、齿圈与筒体过度位置。有限元法修形后最大等效应力集中在齿圈中间截面附近且齿圈圆周方向的应力分布更加均匀。
(4)有限元法修形后柔轮的最大等效应力比线性法修形后减小14.65%,比未修形减小41.79%,说明有限元法修形可以有效解决线性法修形不充分以及未修形时轮齿间的啮合干涉引起应力集中的问题。
