蜗杆砂轮磨削齿向修形齿面扭曲补偿研究*
2023-12-11田晓青武众磊游通飞
田晓青 武众磊 周 蕾 游通飞 韩 江 夏 链
(①合肥工业大学机械工程学院,安徽 合肥 230009;②安徽省智能数控技术及装备工程实验室(合肥工业大学),安徽 合肥 230009)
蜗杆砂轮磨齿是齿轮精加工的常用工艺之一,具有高效率、高精度等特点。为了改善齿轮的工作性能,例如载荷分布、啮合冲击、工作噪声和润滑等,通常需要进行齿面修形[1]。然而蜗杆砂轮磨齿工艺在磨削带齿向修形的斜齿轮时会出现齿面扭曲现象[2],降低齿面精度和传动精度,因此要调整和补偿齿面扭曲。
常用的齿面修形方法分为齿廓修形[3]、齿向修形[4]和拓扑修形。Litvin F L 等[5]通过计算机设计、啮合仿真、应力分析等验证了在传动方面修形齿轮优于未修形齿轮。Tran V T 等[6]将滚刀的对角进给运动设为横向运动的二阶函数,改变滚刀的齿向压力角得到双导程滚刀,验证了在接触和传动性能方面双导程滚刀加工出的齿轮优于传统滚刀加工的。İmrek H 等[7]通过齿向修形让齿面压力分布更加均匀,发现修形齿轮在啮合区域的磨损深度接近均匀。Korta J A[8]等研究了三种模型的适用性,通过找到齿形的最优几何修改数值,降低了齿轮传动误差和齿面接触应力。综上,齿面修形可以提高齿轮的接触性能和传动性能。
齿面扭曲补偿方法可以分为优化砂轮、修形曲线、机床轴附加运动量三类。Graf W 等[9]通过改变砂轮形状引进特定扭曲抵消齿面扭曲。李国龙等[10]将齿向鼓形修形曲线分成三部分,调整每部分曲线的比例因子和鼓形量降低齿面扭曲。何坤等[11]建立X轴、Y轴、C轴附加运动量与齿面扭曲的数学模型,优化轴运动量,消减齿面扭曲。KISSsoft 的工程师[12]在KISSsoft 中获得齿面扭曲值,通过额外的齿面修形量抵消齿面扭曲。
砂轮的优化过程时间长、价格高,而且砂轮的有效使用率低,优化修形曲线存在齿面扭曲补偿效果有限等不足。对机床主从运动轴施加附加运动量,不仅可以实现齿面扭曲的补偿,而且可以克服优化砂轮的缺点。前人通过补偿机床运动轴消减齿面扭曲的研究还存在着机床轴补偿不全面,未考虑运动轴的联动等问题。本研究在前人的基础上,基于柔性电子齿轮箱对主从运动轴施加附加运动量,实现齿面扭曲补偿。
1 齿面扭曲产生原因及数学模型
1.1 齿面扭曲产生原因
如图1 所示,齿面扭曲是指在齿向鼓型修形中,齿轮端截面廓形沿齿向发生扭转的现象。蜗杆砂轮磨削齿轮时,在啮合过程中会形成大量接触迹,并且同一条接触迹上的磨削量相等。对于渐开线直齿齿面或常规加工的渐开线斜齿齿面,由于齿面磨削量相同,不会产生齿面扭曲现象,而齿向修形齿面由于沿着齿向方向截面内磨削量不同,会造成齿面扭曲。
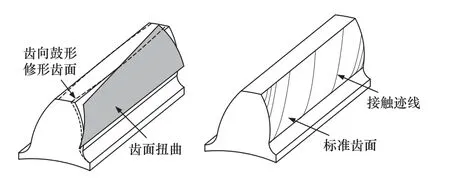
图1 齿面扭曲示意图
如图2 所示,以齿向鼓形修形齿面为例,假设修形曲线是抛物线,因为同一条接触迹上的磨削量相等,则B1点的磨削量与P1点的相等,C1点的磨削量与P2点的相等,所以P点所在截面(B1PC1)的磨削量不相等。同理,齿向任意截面的齿面磨削量都不相等,因此齿面发生扭转。在齿轮两端,齿向修形量最大,修形曲线切线斜率最大,齿面扭转量最大,可以将齿面最大扭转量定义为齿面扭曲值。

图2 齿面扭曲产生原因[12]
1.2 齿面模型的建立
图3 所示为齿轮端截面的廓形,包括齿顶圆弧AB、渐开线BC、齿根过渡圆弧CD、齿根圆弧DE。以齿轮圆心为坐标原点O建立坐标系XOY,竖直向上为X轴正向,水平向右为Y轴正向,C点为渐开线起点,B点为渐开线终点,δ为OE与X轴正向夹角,rb为基圆半径,ϕ为展角θ与压力角α的和。
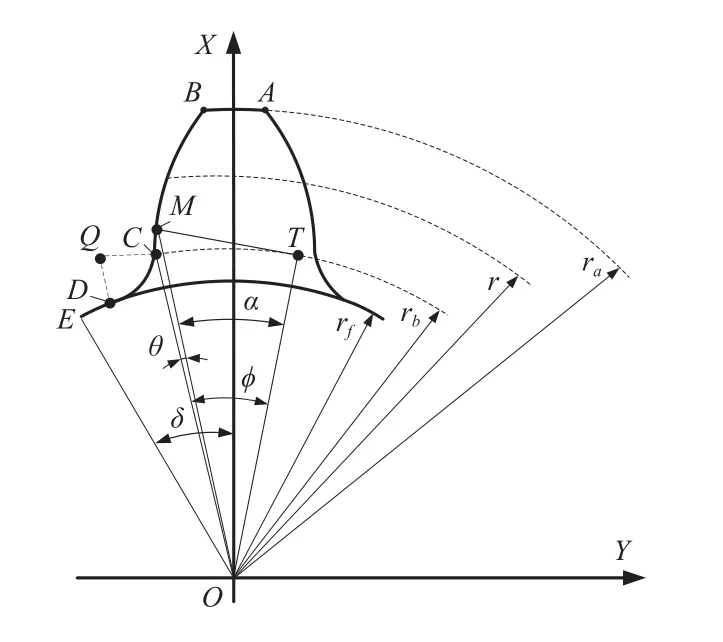
图3 齿轮端截面廓形
以左侧齿面为例,渐开线的参数方程为
将渐开线BC绕着齿轮轴线螺旋旋转得到渐开线齿面[13]:
式中:φ为渐开线绕着齿轮轴线旋转的角度。
对 ϕ 和 φ求偏导后外积可得到曲面的单位法向量ng(ϕ,φ)表达式:
假设齿向鼓形修形曲线方程为G=ρ(pφ-b/2)2,ρ为抛物线系数,b为齿宽,φ为渐开线绕着齿轮轴线旋转的角度,p=rb/tanβb为螺旋参数,所以齿向鼓形修形齿面方程为
其中:Δφ=G/rb。对其中的两个变量 ϕ、φ求偏导得到齿向鼓形修形齿面法向量ng′(ϕ,φ):
1.3 砂轮表面模型的建立
图4 所示为齿轮和砂轮的空间啮合坐标系,坐标系S(O-X,Y,Z)与S p(Op-Xp,Yp,Zp)是空间固定坐标系,坐标系S1(O1-X1,Y1,Z1)与S2(O2-X2,Y2,Z2)分别 与砂轮、齿轮固联,Z1轴、Z2轴分别与砂轮、齿轮回转轴线重合,OOp=a是中心距,Σ是轴交角,OO1=LY是砂轮沿其自身轴线的移动距离,OpO2=LZ是砂轮沿着齿轮轴线的移动距离,这里用齿轮沿着自身轴线的移动距离表示。
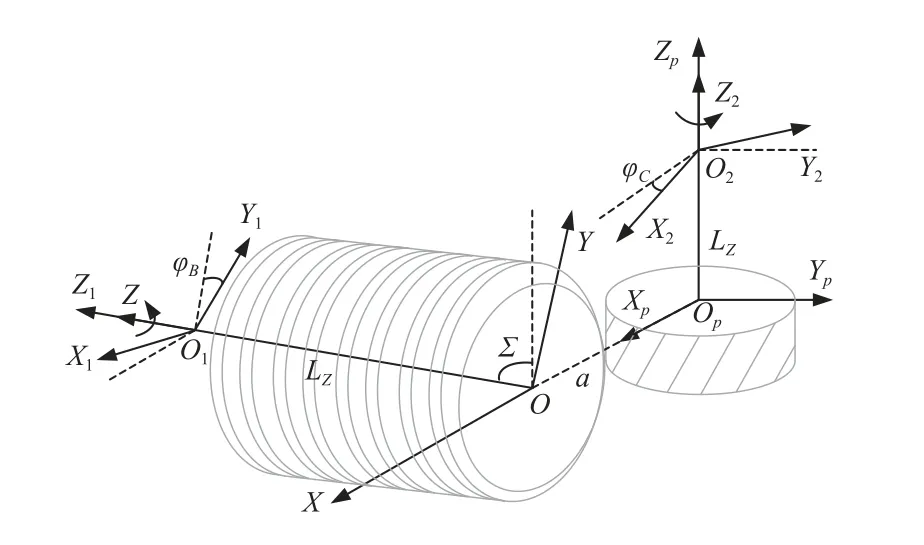
图4 砂轮、齿轮啮合坐标系
在S2(O2-X2,Y2,Z2)下,空间啮合坐标系中某点的 相对 速度v12[14]:
式中:ω1、ω2分别为砂轮和齿轮角速度;vY、vZ分别为Y轴、Z轴的移动速度。
从而得到啮合方程:
由渐开线的性质可知:
在 ΔOMT中,
式中:r为瞬时接触点到齿轮回转轴线的距离,在区间[rf,ra]均匀变化[15];rf为齿根圆半径;ra为齿顶圆半径。由此可求出每个时刻的 ϕ,再代入啮合方程就可求出每个时刻的 (ϕ,φ)。
2 齿面扭曲的补偿原理
2.1 机床运动学建模
齿轮加工机床采用的是重庆机床集团的YW7232CNC 磨齿机,结构简图如图5 所示。参照磨齿机各轴的相对位置关系,建立相邻轴间的坐标变换关系如图6 所示,并且求得坐标变换矩阵。

图5 主要轴示意图

图6 坐标变换关系
根据齐次坐标变换得到砂轮坐标系到工件坐标系的坐标变换矩阵:
MCO、MXO、MZX、MAZ、MYA、MBY分别是床身到C轴、床身到X轴、X轴到Z轴、Z轴到A轴、A轴到Y轴、Y轴到B轴的变换矩阵。φA、φB、φC、LX、LY、LZ分别表示A轴、B轴、C轴、X轴、Y轴、Z轴的运动量,φB=ω1t,φC=ω2t。
2.2 基于电子齿轮箱的齿面扭曲补偿
电子齿轮箱可以取代机床内联传动链,保持多个运动轴实现定速比、变速比联动关系。电子齿轮箱的结构分为主从式和并行式,因为蜗杆砂轮磨齿时,主轴参与联动,转速大,还有严格的位置和速度要求,所以本文将主从式和并行式电子齿轮箱组合使用。基于电子齿轮箱的齿面扭曲补偿原理如图7 所示。各轴 理论运动量 φBM、φCM、lXM、lYM通过电子齿轮箱施加附加量(ΔφB、ΔφC、ΔlX、ΔlY、ΔlZ)获得各轴实际运动量 φBA、φCA、lXA、lYA、lZA。
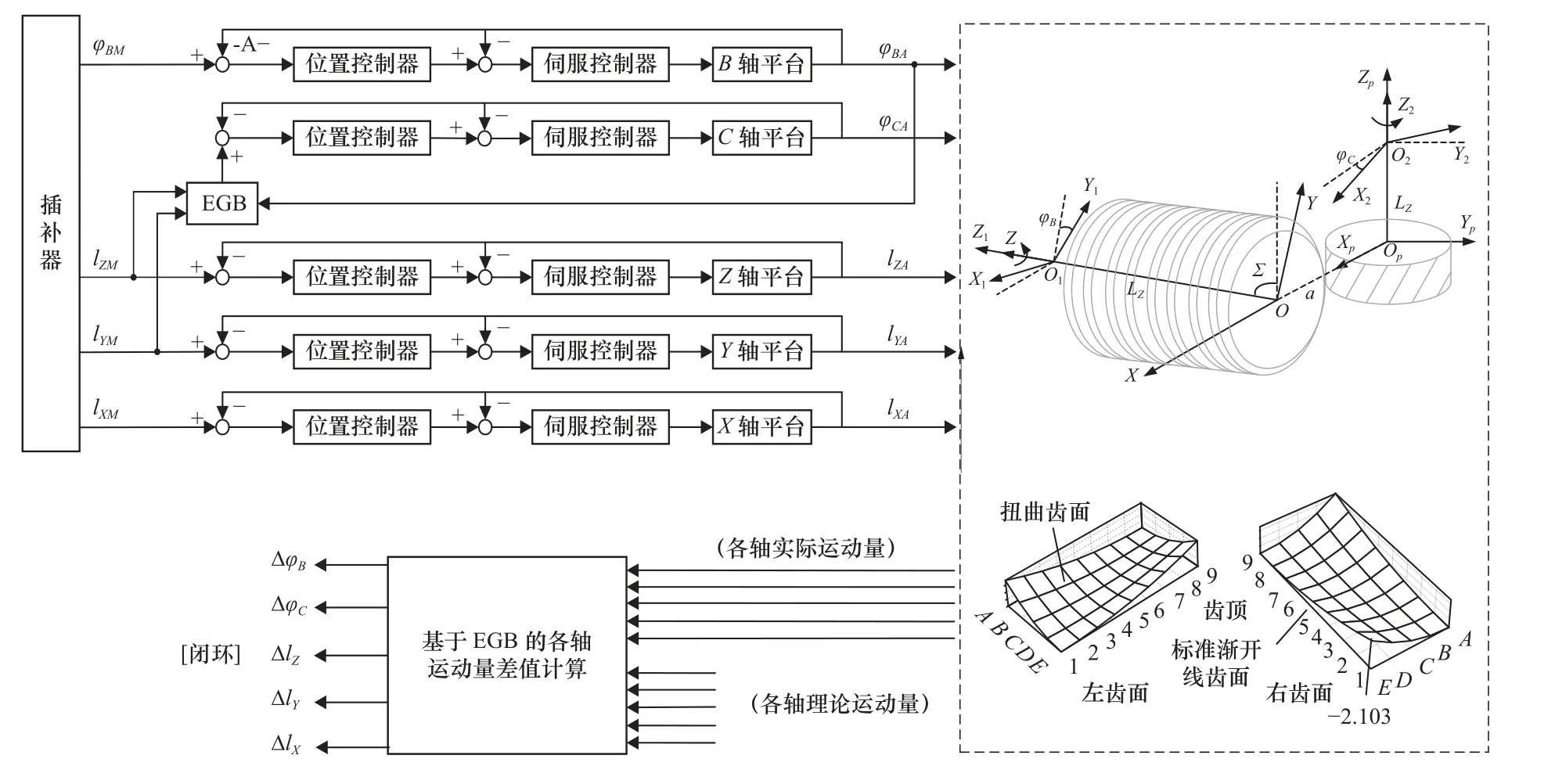
图7 齿面扭曲补偿原理
蜗杆砂轮磨齿机电子齿轮箱的B轴、C轴、Y轴、Z轴联动关系[16]为
式中:nB、nC分别为B轴、C轴的转速;Z1、Z2分别为砂轮头数和齿数;β、λ分别为齿轮螺旋角和刀具安装角,deg,齿轮右旋时螺旋角为正,左旋时螺旋角为负;mn为法面模数,mm。
kB、kZ、kY为常量,砂轮右旋时kB=1,砂轮左旋 时kB=-1 ;当vZ<0、β >0 时,kZ=1 ;当vZ<0、β <0 时,kZ=-1 ;当vZ>0、β >0 时,kZ=-1;当vZ>0、β <0 时,kZ=1 ;当vY>0 时,kY=1;当vY<0 时,kY=-1。
令砂轮在S1(O1-X1,Y1,Z1) 下的位姿PB为
式中:NX、NY和NZ分别为S1(O1-X1,Y1,Z1)坐标系下的砂轮X轴、Y轴和Z轴法向量,xt、yt和zt分别为S1(O1-X1,Y1,Z1)坐标系下的砂轮坐标。
则:
用 φBM、φCM、lXM、lYM、lZM表示与齿向鼓形 修形齿面位姿对应的主从动轴运动量,分别代入MBC和式(6)与式(7)中的 φB、φC、LX、LY、LZ,得到:
得到啮合方程为
由式(4)~式(14)通过运动学逆解[16]解得φBM、φCM、lXM、lYM、lZM。
同样地,对于扭曲齿面,可以测量出齿面坐标,求出齿面法向量,从而求出与扭曲齿面位姿对应的主从动轴运动量 φBT、φCT、lXT、lYT、lZT。
将齿向鼓形修形齿面位姿与扭曲齿面位姿对应的主从动轴运动量相减便能得到主从运动轴的附加运动量,见式(15)。主从运动轴附加运动量可在通过机床虚拟轴实现。
补偿齿面扭曲时,φBT、φCT、lXT、lYT、lZT分别加上各自的附加运动量作为实际运动量,见式(16),其中ki(i=1,2,3,4,5)是补偿系数,并且可以取不同值。
3 数值实例验证
基于Matlab 的数值实例仿真验证上述理论和模型的正确性,采用的齿轮和砂轮基本参数见表1,利用KISSsoft 软件计算出该参数下齿轮的合适鼓形量Cp为21.65 μm。图8 所示为齿向鼓形修形曲线,可以求得抛物线系数 ρ 为 -5.41×10-5。
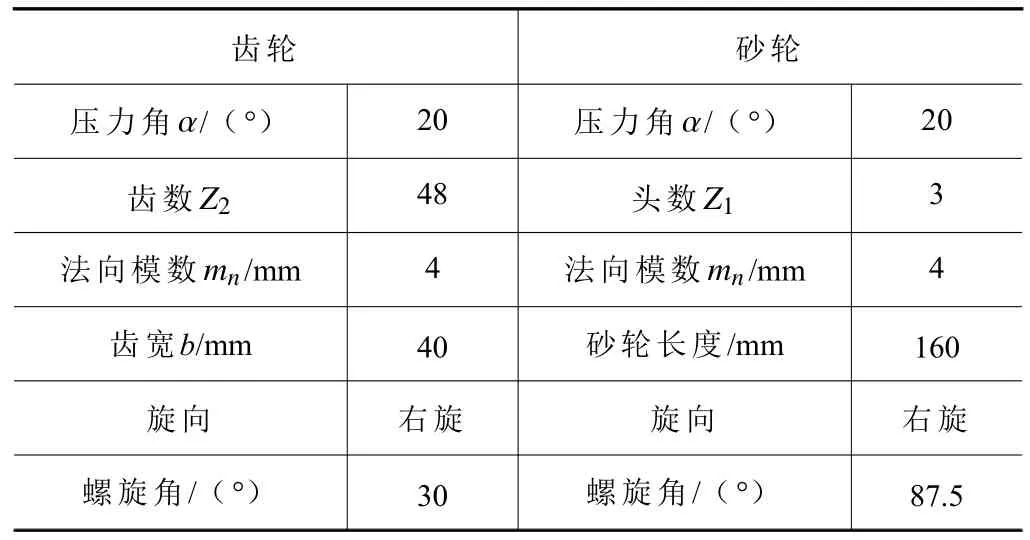
表1 基本参数

图8 齿向鼓形修形曲线
齿面网格化时,为了使啮合区域集中在中间,避免齿根、齿顶的接触以及齿轮倒棱工艺的影响,齿顶、齿根分别缩进工作齿高的5%,齿轮两端分别缩进齿宽的5%,齿面网格化得到5×9 个点。齿向鼓形修形齿面仿真结果如图9 所示,以左齿面为例,齿向鼓形修形齿面相对于标准渐开线齿面的法向偏差见表2。

表2 齿向鼓形修形齿面法向偏差 μm

图9 齿向鼓形修形齿面
扭曲齿面根据扭曲值大小公式[17]C=(8CpLαtanβb)/b构造,其中 βb为基圆螺旋角,Lα为渐开线长度,b为齿宽。扭曲齿面仿真结果如图10 所示,齿面扭曲在齿向修形斜齿齿面的齿根和齿顶扭曲值最大。以左齿面为例,扭曲齿面相对于标准渐开线齿面的法向偏差见表3。

表3 扭曲齿面法向偏差 μm

图10 扭曲齿面
齿面扭曲补偿结果仿真如图11 所示,当补偿主从动轴运动量时,在图11a、11b、11c 中补偿系数ki(i=1,2,3,4,5)分别为0.5、1、1.5,意味着图11a、11b、11c 分别代表欠补偿、理想补偿、过补偿。
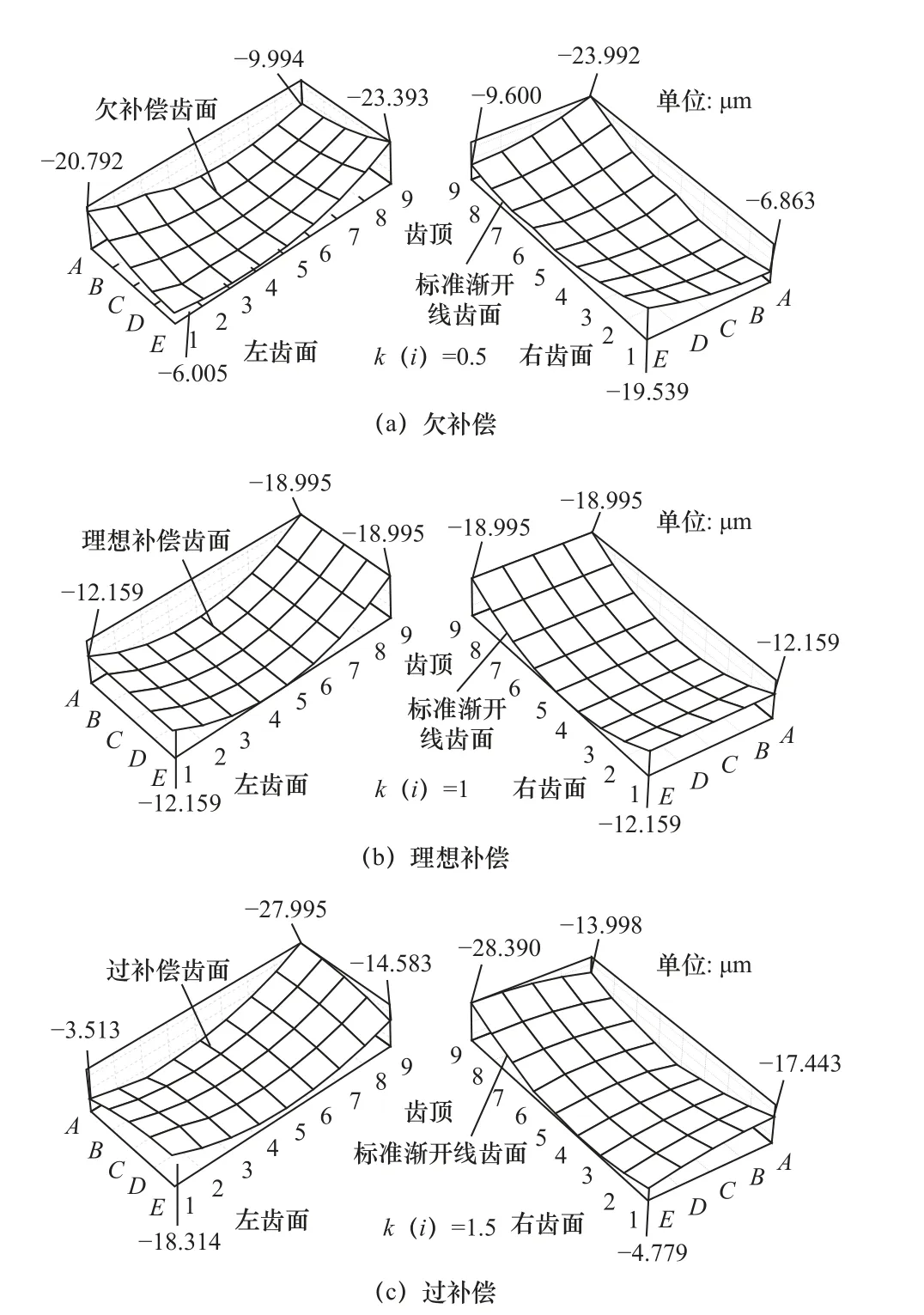
图11 补偿结果
如图9~图11 的仿真结果所示,扭曲齿面经过欠补偿和过补偿,虽然齿面扭曲得到一定抑制,但是法向偏差值依然偏离齿向鼓形修形齿面法向偏差值,补偿效果欠佳。理想补偿的齿面效果最好,所以我们在实际补偿过程中要尽量接近理想补偿。
4 齿面接触分析
构建一个单级齿轮副传动系统,基本参数见表4所示。在齿轮分析软件KISSsoft 中分别建立上述标准渐开线齿面、齿向鼓形修形齿面、扭曲齿面和补偿后的齿面,以左齿面为工作齿面进行齿面接触分析,参数设置见表5,结果得到图12~图15 所示的齿面法向力和接触应力分布。
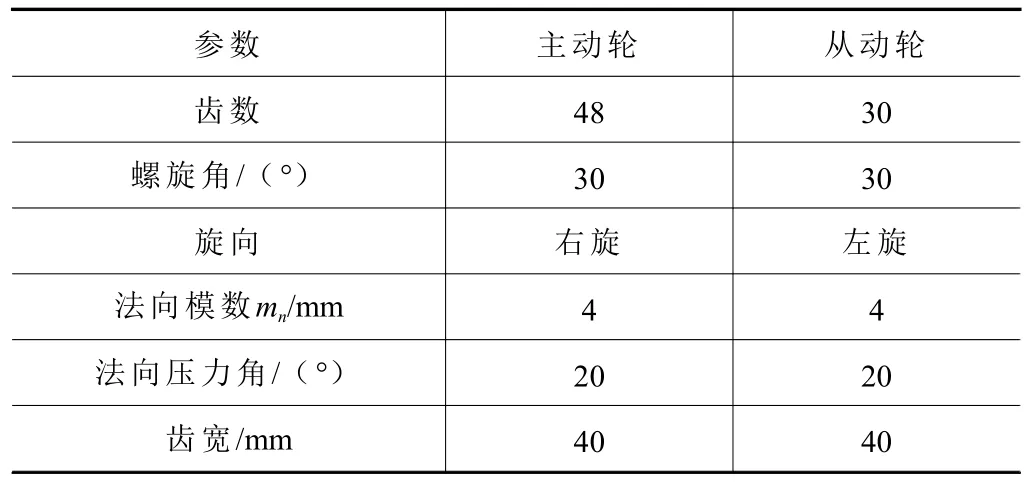
表4 单级齿轮副基本参数
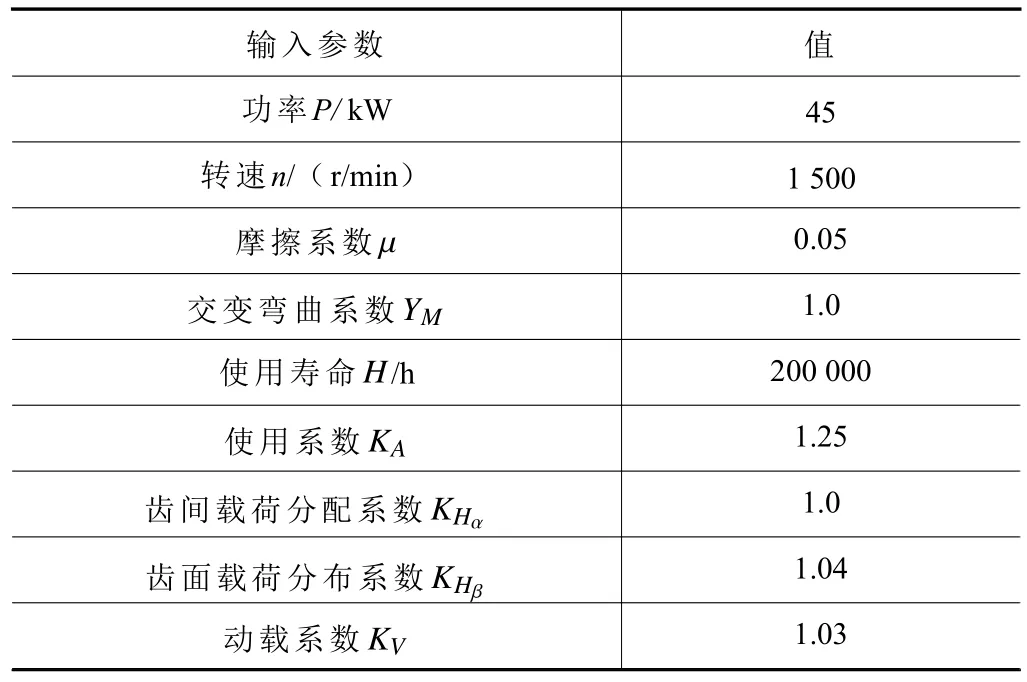
表5 齿面接触分析基本参数

图12 标准齿面的法向力(左)和接触应力(右)

图13 齿向鼓形修形齿面的法向力(左)和接触应力(右)
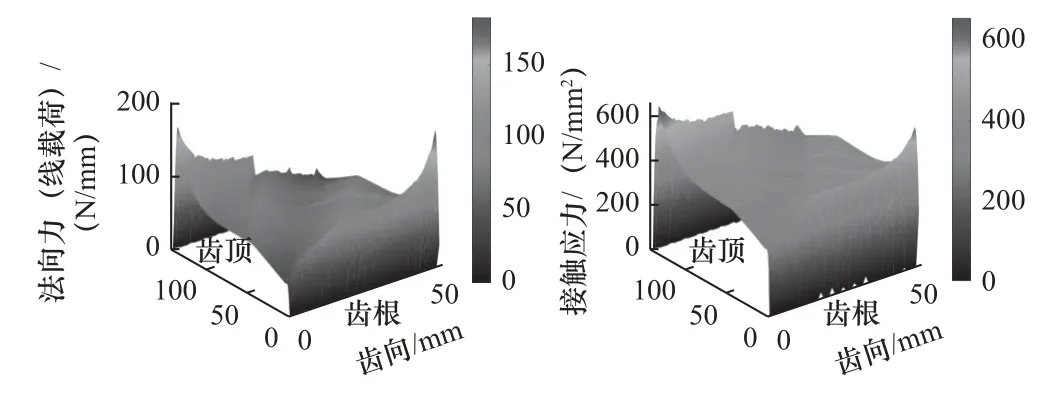
图14 扭曲齿面的法向力(左)和接触应力(右)
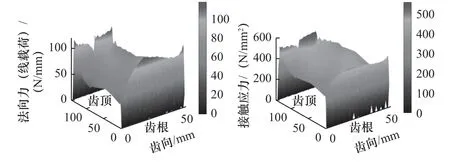
图15 理想补偿后的齿面的法向力(左)和接触应力(右)
根据图12~图15 的分析结果,标准渐开线齿面经过齿向鼓形修形以后,最大法向力从145.635 N/mm 降到了117.450 N/mm,最大接触应力从622.564 N/mm2降到了559.533 N/mm2。齿面发生扭曲以后,最大法向力升到了182.696 N/mm,最大接触应力升到了675.087 N/mm2。经过理想补偿后的齿面,最大法向力降到了124.672N/mm,最大接触应力降到了558.210 N/mm2。
由图16 和图17 可知,扭曲齿面的法向力较为集中,且数值较大,经过理想补偿之后,齿面法向力分布均匀,数值减小。比较齿向鼓形修形齿面和理想补偿后齿面的法向力和接触应力,两者的啮合性能基本相同,实现了扭曲补偿的预期效果。

图16 扭曲齿面的法向力分布
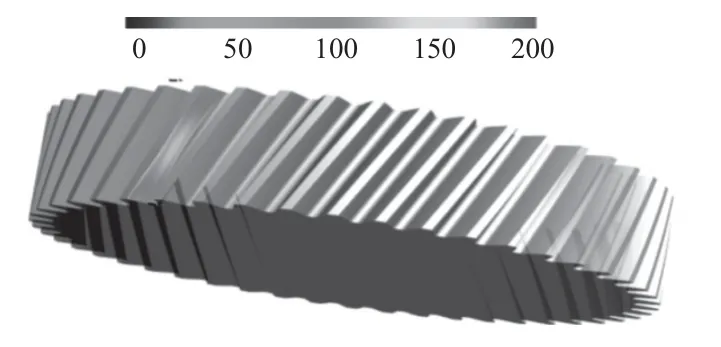
图17 理想补偿后的齿面法向力分布
5 齿面扭曲机床加工实验验证
在重庆机床集团生产的YW7032 数控万能磨齿机上进行加工验证,如图18 所示。加工没有扭曲补偿和带有扭曲补偿的齿向修形齿轮,分别进行齿面检测并生成齿面检测报告,从而验证齿面扭曲现象以及本文研究方法对齿面扭曲现象的抑制效果。

图18 YW7032 磨齿机
加工采用的金刚轮和蜗杆砂轮如图19 所示,其基本参数见表6。

表6 金刚轮和蜗杆砂轮基本参数

图19 刀具
图20a 所示为待加工齿轮,精度为7 级。该齿轮经过滚齿加工和高频淬火,其基本参数和表1 一致。

图20 修形前后的齿轮
在机床上进行齿向修形齿轮的加工。齿向修形界面如图21a 所示,在齿向修形选项中输入齿向修形齿轮的数据H(修形曲线长度)、HH(修形曲线总长度的一半)、LL(修形曲线斜率)和LC(修形曲线鼓形量)。本次修形选择的修形曲线是抛物线,H为40 mm,HH为20 mm,LL为0,LC为0.02 mm。图20b 所示为没有扭曲补偿的齿向修形齿轮,在齿轮检测仪——哈尔滨精达JE32 齿轮测量中心上生成检测报告,如图22 所示。
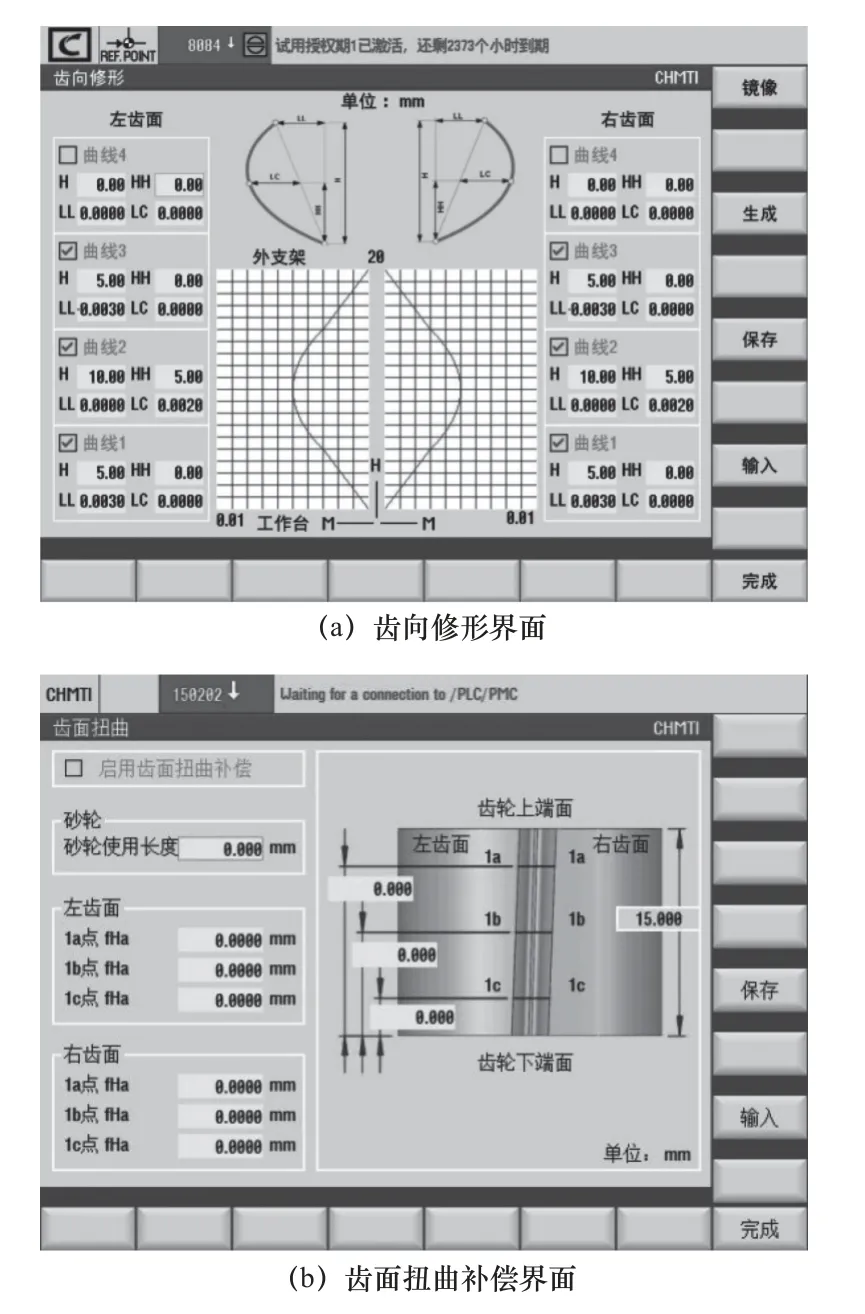
图21 齿面设计
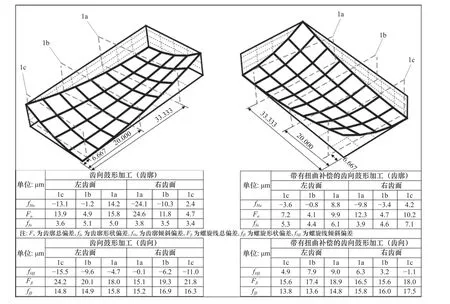
图22 齿面检测报告
图21b 所示为扭曲齿面补偿界面。对齿向鼓形加工齿面和带有扭曲补偿的齿向鼓形加工齿面的1a、1b 和1c 这3 个截面进行测量,获得齿面检测报告,如图22 所示。由齿面检测报告可以看到,同一齿面的齿廓倾斜偏差fHα同时出现正负,说明有齿面扭曲现象的存在。
靠近齿轮两端的齿面扭曲现象最严重,所以用齿面1a 和1c 处的fHα之差的绝对值来表示齿面扭曲程度。经过齿面扭曲公式计算的齿面扭曲值为20.7 μm。图22 中,齿向鼓形加工左齿面的扭曲值为27.3 μm,右齿面的扭曲值为26.5 μm,与计算值接近;带有扭曲补偿的齿向鼓形加工左齿面的扭曲值为12.4 μm,右齿面的扭曲值为14 μm。通过对比可以看出,齿面扭曲补偿后,齿面扭曲程度降低,齿面精度提高。
6 结语
(1)详细分析了齿面扭曲的产生机理,建立渐开线斜齿面和齿向鼓形修形齿面模型。
(2)利用齐次坐标变换建立了砂轮与标准齿轮、齿向鼓形修形齿轮以及齿面扭曲齿轮之间的变换矩阵,根据齿轮啮合和运动学逆解得到了基于电子齿轮箱的齿面位姿与主从动轴运动量之间的关系,通过对主从运动轴施加附加运动量,实现对齿向修形扭曲齿面的补偿,Matlab 仿真说明该方法具有有效性和正确性。
(3)在考虑电子齿轮箱的同时补偿了主从动轴的运动量,保证了B轴、C轴、Y轴、Z轴在加工过程中的联动关系,提高了齿面扭曲补偿的可靠性和精度。
(4)在YW7032 磨齿机上加工了没有扭曲补偿和具有扭曲补偿的齿向鼓形修形齿轮,生成齿轮检测报告,证明了齿向鼓形加工齿面会有扭曲现象产生,经过扭曲补偿的齿轮,扭曲程度降低。
