速度PI 控制及低通滤波器的系统设计
2023-12-11章国光陈超凡郑晓斌刘文龙
章国光 陈超凡 郑晓斌 刘文龙
(①湖北工业大学电气与电子工程学院,湖北 武汉 430070;②湖北韵生航天科技有限公司,湖北 襄阳 441000)
在工业控制伺服系统中,电机与负载之间一般通过传动轴、齿轮或者联轴器等传动机构进行连接,因此电机和负载之间存在弹性传动,使系统出现机械谐振现象。机械谐振会造成很多不利的影响,如振荡产生噪声、降低伺服系统性能,严重时甚至损坏机械系统。因此,机械谐振抑制已经成为高性能伺服驱动系统的重要研究课题之一[1]。
现代伺服驱动系统通常采用主动方式和被动方式抑制机械谐振,主动方式需要主动调整控制器参数或结构来消除谐振带来的影响,被动方式是通过滤波器等来实现的。文献[2]基于传统PI(比例积分)控制的二惯性弹性系统,利用相同实部、半径和阻尼系数的极配置法来分析系统的阻尼特性,并实现控制器的参数的优化配置。文献[3]分析电机转速PI 控制、加速度反馈等方法在抑制振荡和抑制干扰方面的关系,介绍了一种基于极配置的分析框架,评价了各种设计方案的设计特征。文献[4-5]分析PI 控制下不同反馈控制的效果。文献[6]提出了转速负反馈抑制谐振的结构和反馈系数的设计方法,证明转速负反馈对负载惯量变化的鲁棒性。文献[7-8]提出了参数平面法,通过建立系统特征方程与2 个控制参数之间直接的联系,通过代数矩阵,实现系统参数的求解,系统设计的自由度较高。因此本研究将参数平面法应用到速度控制系统中。
陷波器可以抑制谐振引起的幅值,并通过适当的参数设置提高系统的动态性能[9]。文献[10]在传统扰动观测器的基础上引入高通滤波器以消除轴转矩观测量的直流分量,从而增大系统阻尼来抑制谐振,同时改善系统动态响应性能。
本文应用参数平面法设计PI 速度控制系统,二参数平面法的设计可以方便地调节系统中支配极的位置,通过配置约束极的位置来分析系统阻尼特性。针对欠阻尼情况,导入滤波器,并利用三参数扩充参数平面法[11]进行系统分析,解析系统的特征与系统参数调节的规律。
本文导入扩充参数平面法,对于高阶控制系统改善其设计自由度,且计算简单。同时,针对滤波器的导入,结合系统的阻尼特征,给出系统参数的调节方法。
1 二惯性系统与系统建模
二惯性系统由一个弾性驱动轴和两个惯性组成,模型如图1 所示。
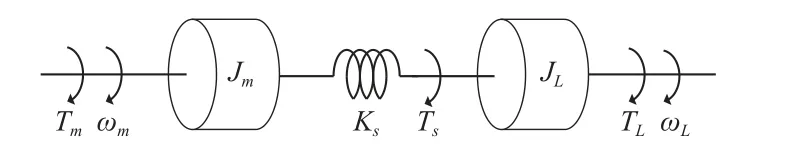
图1 二惯性系统模型
图1 中,Jm为电机转动惯量(kg·m2),JL为负载转动惯量(kg·m2),Tm为电机转矩(N·m),Ts为传动轴转矩(N·m),TL为负载转矩(N·m),ωm为电机转速(rad/s),ωL为负载转速(rad/s),Ks为传动轴扭转刚度(N·m/rad)。
一般情况下,二惯性系统的机械阻尼较小,在分析时可以忽略。为了进一步分析二惯性弹性系统,建立其框图和传递函数。二惯性系统框图如图2所示。
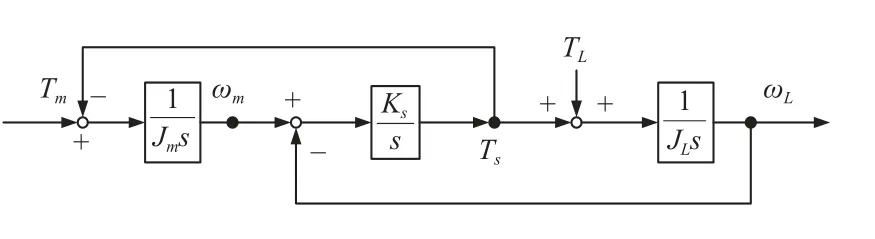
图2 二惯性系统框图
由图2 可以得到,从电机转矩Tm到电机转速ωm和负载转速 ωL的传递函数:
式中:ωa为反谐振频率,ω0为谐振频率,R为负载与电机的惯性比。
2 系统的设计与分析
2.1 速度控制系统
速度控制系统框图如图3 所示。
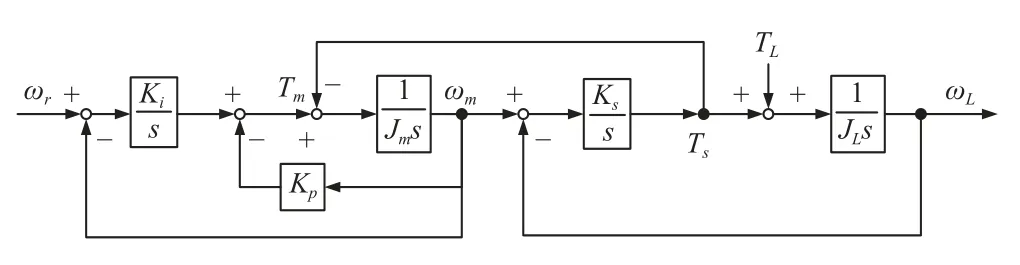
图3 速度系统框图
图3 中,Kp为比例反馈系数,Ki为积分反馈系数,ωr为电机的参考输入转速。
由图3 可以得到从电机参考输入转速 ωr到电机转速 ωm和到负载转速 ωL的传递函数:
该系统有四个极点需要分配,但只有Kp和Ki两个控制参数,控制阶数高,可控参数少,因此可使用二参数设计的参数平面法。
2.2 参数平面法的设计导入
通过对速度控制系统进行分析,得出其极点分布,验证参数平面法对系统参数调节的可行性。式(5)的设计式样为
式中:ω1为设计极角频率,ω2为约束极角频率(假定 ω1<ω2),ζ1、ζ2为相对阻尼系数。
参数平面法的设计计算过程以及系统特征方程的一般形式为
式中:ak为特征方程的各阶系数,m为系统阶数。
复极s1,2表示为
式中:函数Uk(ζ1) 为第二类切比雪夫函数,参数ζ1的范围为 0 ≤|ζ1|≤1,表达式为
将式(9)代入特征方程式(7)中,令实部和虚部之和各自为零后得到:
系数ak作为控制参数Kp和Ki的函数:
式中:bk、ck、dk为系统结构系数。
式(11)可表示为
求解式(13),可以计算出控制参数Kp和Ki:
可以通过调节设计极角频率和阻尼系数的值来设计控制参数Kp和Ki。本研究通过参数平面法建立了特征方程根与两个控制参数之间的关系来解析系统[7-8]。
参数平面法的导入过程如下,速度控制系统分母的各阶系数从式(5)中得到,分别为
式中:bk、ck、dk各系数按式(12)展开顺序,并对照式(16)各系数后得到:
而bk、ck、dk的其他各系数均为0。
将式(17)代入式(14)可求得B1、B2、C1、C2、D1、D2,再根据式(15)可计算出Kp和Ki。
以上,参数平面法提供了二参数系统的计算方法,对于PI 速度控制系统的Kp、Ki两个控制参数,通过参数平面法可以进行参数计算。
2.3 速度PI 控制系统的仿真分析
传动轴扭转刚度Ks=2.33 N·m/rad,负载侧转动惯量JL=1.3×10-4kg·m2。通过改变设计极分析极点分布(图4 中*为设计极,×为约束极),调查设计极、惯性比等特征参数对系统阻尼的影响。
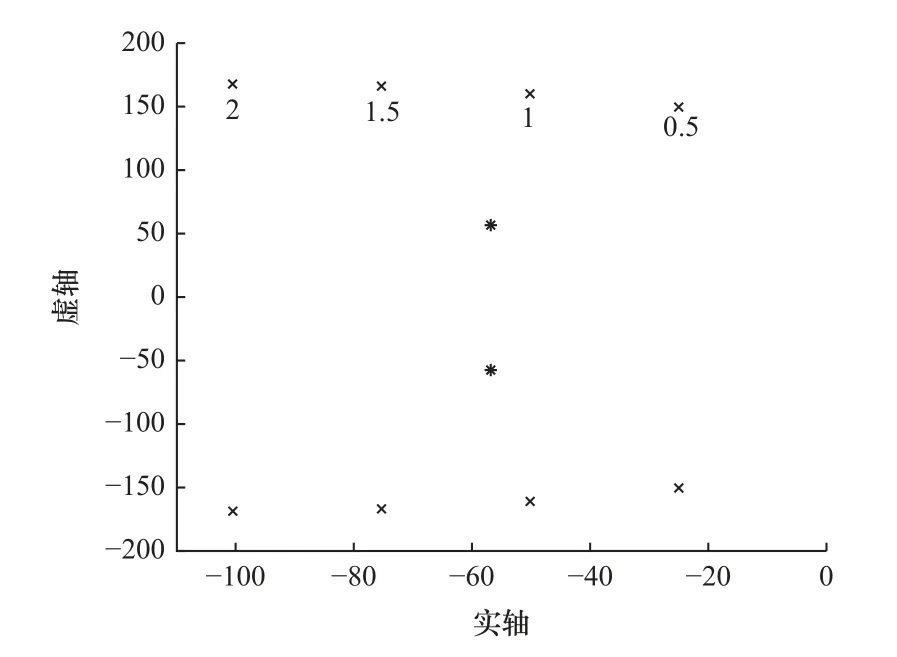
图4 极点分布(ω1=0.6ωa)
(1)设计极ω1=0.6ωa、0.8ωa,阻尼系数ζ1=0.707,惯性比R=0.5~2,系统极分布如图4 和图5 所示。
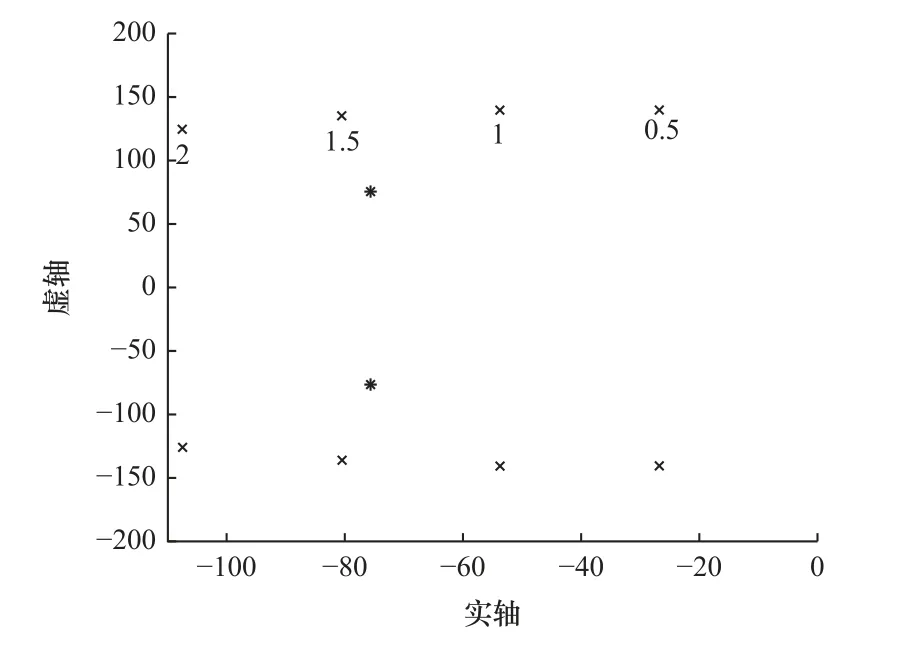
图5 极点分布(ω1=0.8ωa)
由图4 和图5 可以看出,约束极的位置会随着惯性比的增大而远离虚轴。由此可以得出:惯性比相对小时系统的阻尼特性变差。
(2)惯性比R=0.56、0.73,设计极频率ω1=0.3ωa~0.9ωa,PI 控制系统极点分布如图6 和图7所示。
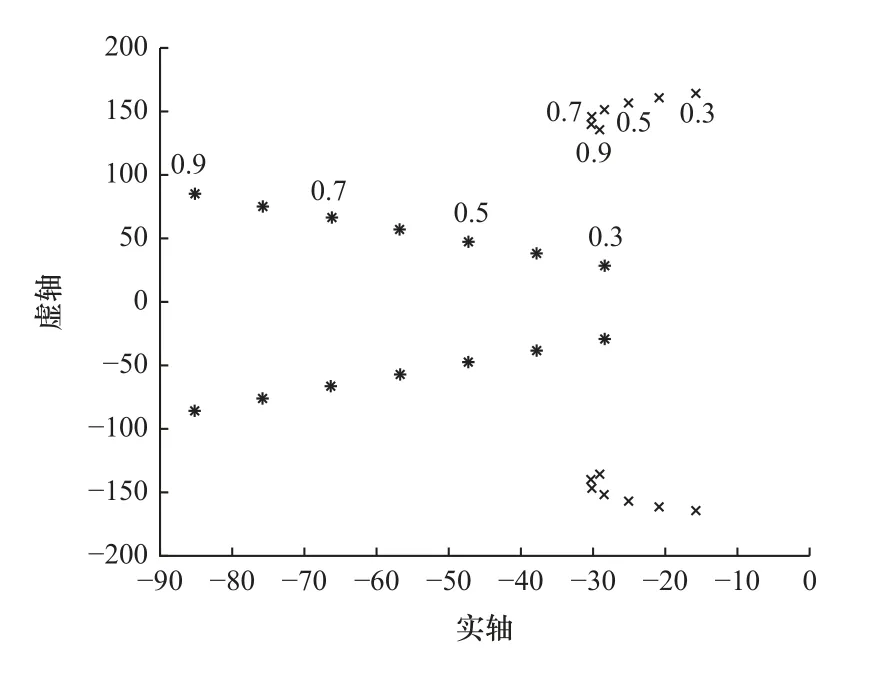
图6 极点分布(R=0.56)
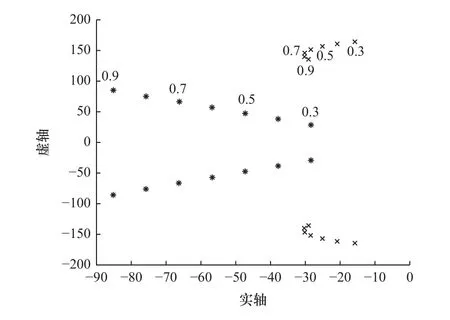
图7 极点分布(R=0.73)
由图6 和图7 可以看出,约束极位置随着设计极频率的增大而远离虚轴,而设计极频率增大到一定程度后,约束极位置又会靠近虚轴。由此可以得出:增大设计极频率的值在一定程度上可以提高系统的阻尼特性,但超出某一范围后,系统阻尼特性反而变差。
(3)设计极 ω1=0.6ωa、0.8ωa,惯性比R=0.56、0.73、1,负载侧阶跃响应曲线如图8 和图9 所示。

图8 阶跃响应曲线(ω1=0.6ωa)
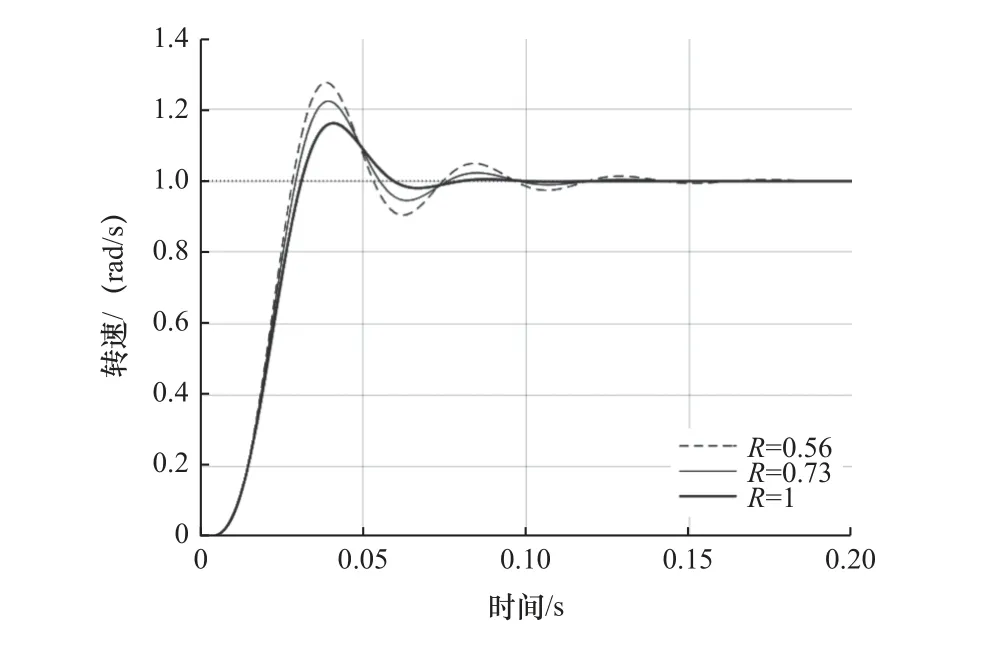
图9 阶跃响应曲线(ω1=0.8ωa)
通过图8 和图9 可以看出,当R<1时,系统呈现欠阻尼特性,系统发生振荡。针对欠阻尼情况,需导入新的方法来改善系统阻尼特性。
3 滤波器的导入与设计分析
3.1 滤波器的建模与设计
伺服系统机械谐振是一种常见的问题,为了解决这个问题,考虑导入低通滤波器进行机械谐振的抑制。在伺服系统中,滤波器通常被放置在控制器的控制回路中,以滤除机械谐振的信号。通过结合控制器与滤波器参数,抑制机械谐振。
含滤波器的PI 速度控制系统(以下简称为IPF)框图如图10 所示。
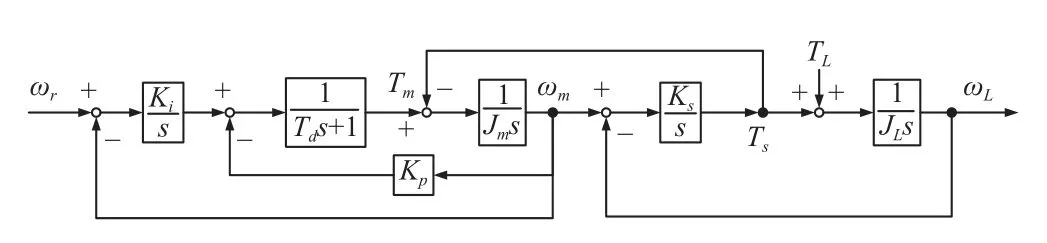
图10 IPF 速度系统框图
图10 中,Td为滤波器时间常数。
由图10 可以得出从电机参考输入转速 ωr到负载转速 ωL的传递函数:
该系统为五阶,但只有Kp、Ki和Td3 个控制参数。
导入扩充参数平面法求解三控制参数。扩充参数平面法建立了特征方程根与控制参数之间的直接关联,可以对三参数系统的控制参数进行解耦计算。
系统特征方程的各阶系数为
IPF 速度控制系统有3 个设计参数,通过配置3 个设计极来开展解析,步骤如下。
复极s1,2和实极s3分别设定为
借鉴第2 节的参数平面法思路,将sk代入特征方程中,并令其实部和虚部之和各自为零后得到:
ak作为控制参数Kp、Ki和Td的函数:
式中:bk、ck、dk、ek为系统结构系数。
式(21)可表示为
通过式(23),可以计算出3 个控制参数Kp、Ki和Td:
bk、ck、dk、ek各系数按式(22)展开顺序,对照式(19)各系数后得到:
而bk、ck、dk、ek的其他各系数均为0。
将式(26)代入式(24)可求得B1、B2、B3、C1、C2、C3、D1、D2、D3、E1、E2、E3,最后,根据式(25)即可计算出Kp、Ki和Td。
3.2 仿真分析
在上述系统结构参数不变的情况下,将PI 控制系统和IPF 控制系统作对比。
(1)当设计极 ω1=0.6ωa、0.8ωa,ω2=ω1,惯性比R=0.5~2时IPF 系统极点分布(*为设计极,×为约束极)如图11 和图12 所示。
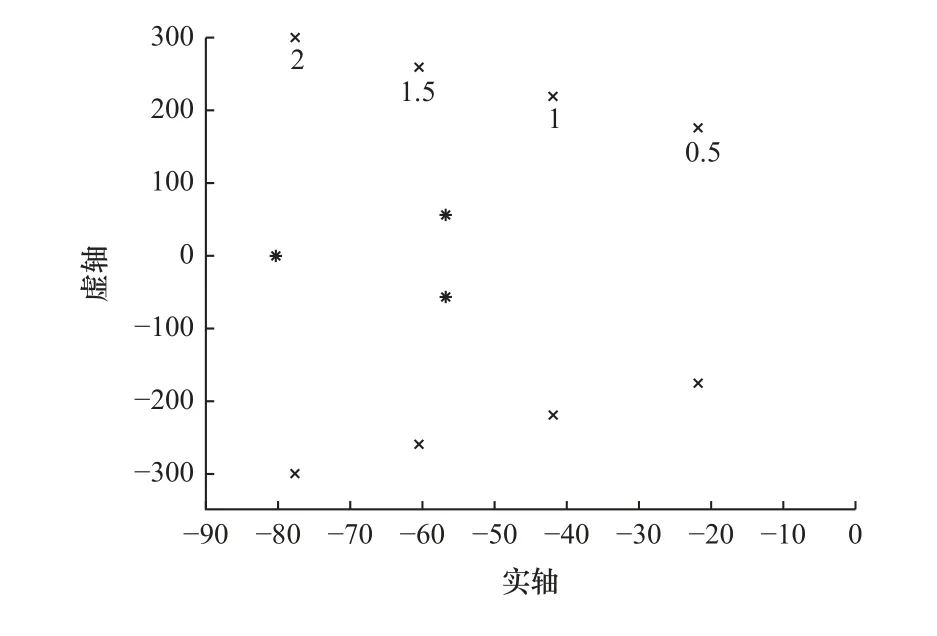
图11 IPF 极点分布(ω1=0.6ωa)
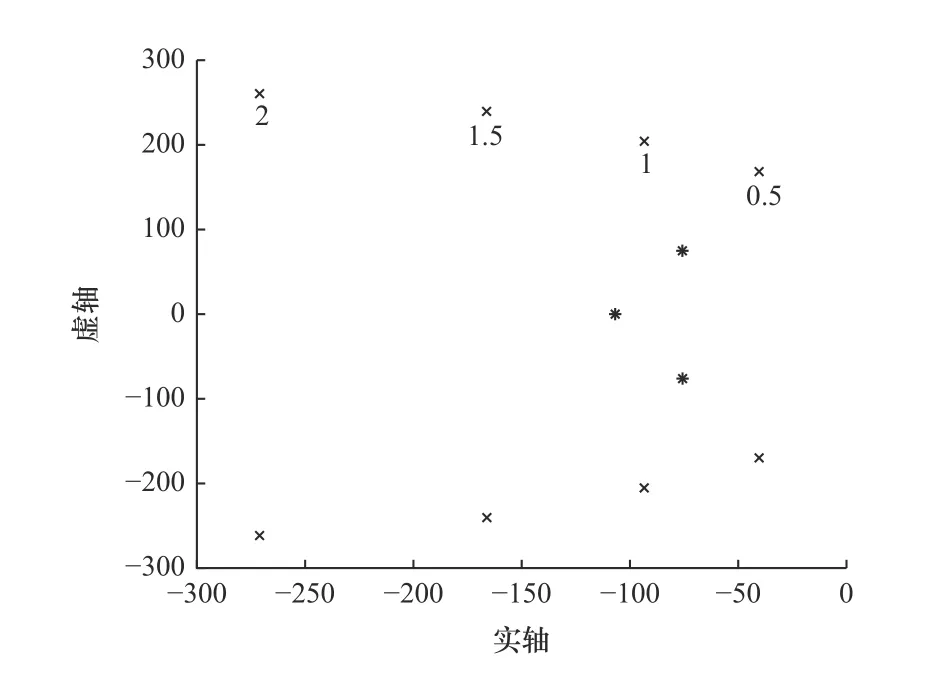
图12 IPF 极点分布(ω1=0.8ωa)
通过图11 和图12 与图4 和图5 对比可以看出,在PI 系统中导入滤波器后,约束极(×)的位置向左移动,说明系统阻尼特性得到改善。
(2)当惯性比为0.56、0.73 和1 时,负载侧阶跃响应曲线如图13 和图14 所示。
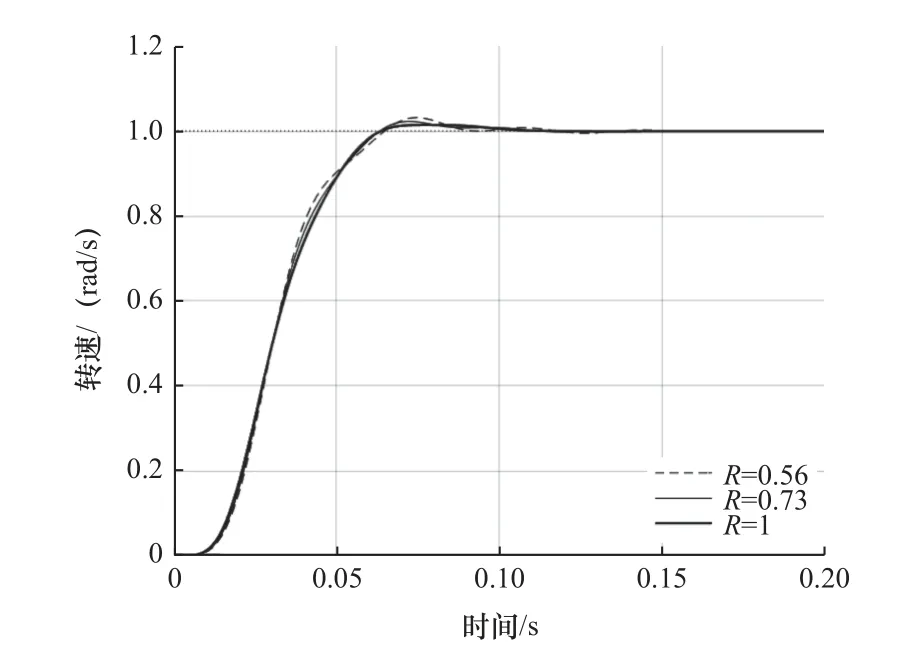
图13 IPF 阶跃响应曲线(ω1=0.6ωa)
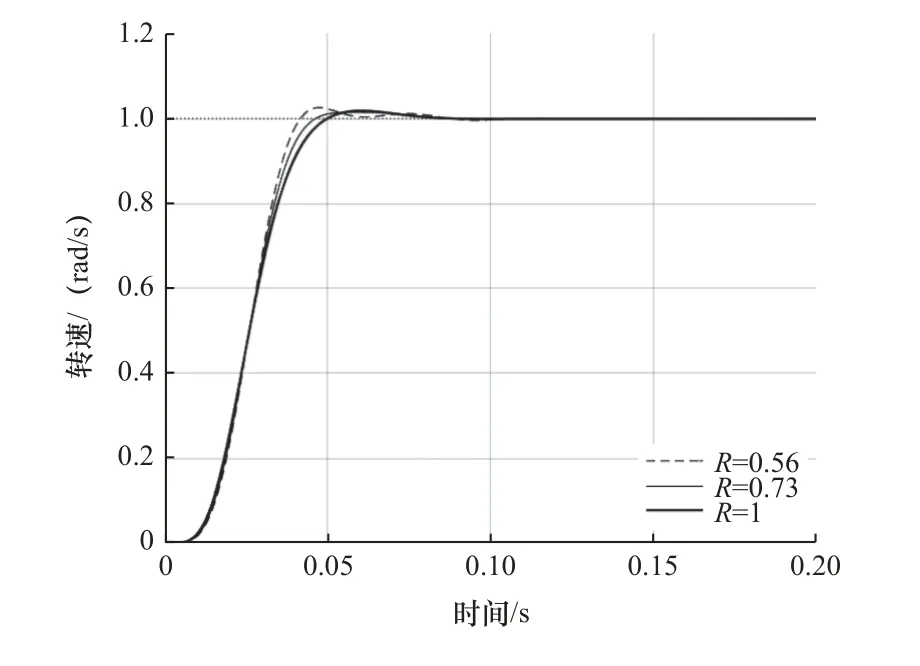
图14 IPF 阶跃响应曲线(ω1=0.8ωa)
图13 和图14 与图8 和图9 对比可以看出,在控制系统中导入滤波器后,系统振荡减小;说明在PI 控制系统中导入滤波器可以提高系统的阻尼特性,有效抑制系统中的机械谐振。
4 实验结果
对二惯性系统进行实验,两台永磁电机通过弹性轴连接。其中一台作为驱动电机,另一台作为负载。电机位置传感器为磁阻传感器,转速通过传感器位置计算得到。惯量盘固定在电机侧和负载侧的传动轴上,通过改变惯量盘的大小改变特性,调节负载侧与电机侧之间的惯量比。图15 所示为实验系统。

图15 实验系统
系统参数见表1。

表1 系统参数
设定电机的参考输入转速为1 000 r/min,对系统的设计进行实验测试。
当设计极频率 ω1=0.8ωa、惯性比为0.56 和0.73时,负载侧阶跃响应曲线如图16 和图17 所示。
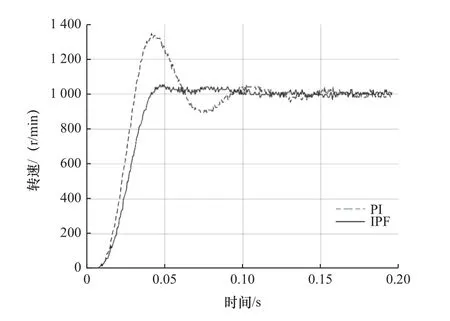
图16 阶跃响应实验(R=0.56,ω1=0.8ωa)
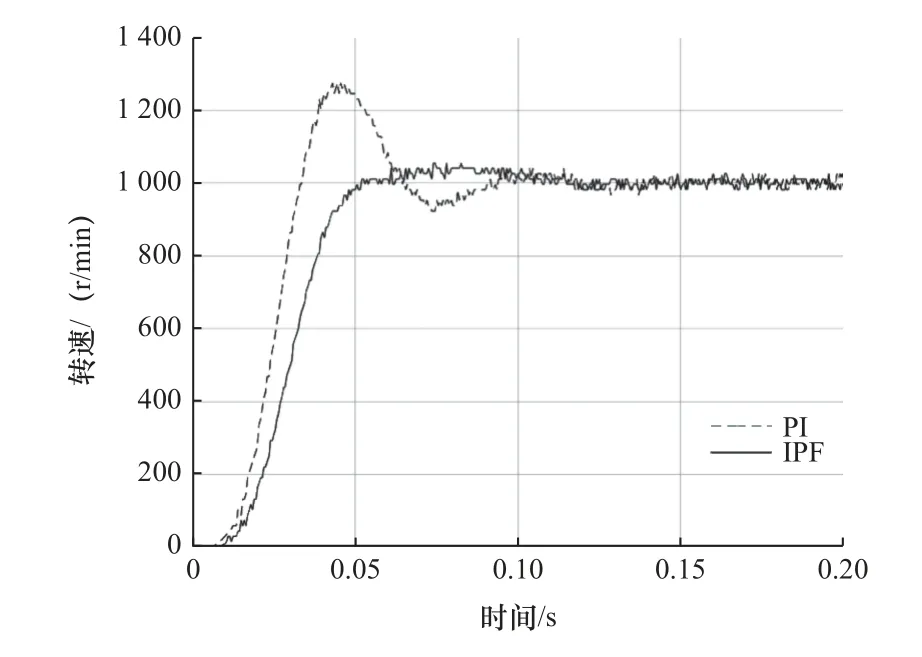
图17 阶跃响应实验(R=0.73,ω1=0.8ωa)
图16 和图17 与图9 和图14 对比可以看出,IPF控制提高了系统的阻尼特性,且实验结果符合仿真分析。
5 结语
本文针对速度PI 控制系统应用参数平面法,解析系统的阻尼特性,分析表明系统小惯量比时呈现欠阻尼特性。
针对欠阻尼特性,在系统中导入低通滤波器,提高系统的阻尼特性。同时导入扩充参数平面法,开展系统仿真及分析,实验结果表明导入滤波器并结合传统的PI 控制可以解决系统欠阻尼特性的问题。
本文解决了五阶三参数系统设计自由度不足的问题,并提出了PI 控制器与滤波器结合的控制与设计法。研究结果表明,扩充参数平面法对二惯性系统三参数调节的直观性、简便性和实用性。
