基于压入法原理测试混凝土超早期弹性模量
2023-12-10王冬丽赵庆新董炳强杨泽宇袁丽丽
王冬丽, 赵庆新, 董炳强, 杨泽宇, 袁丽丽
(1.东北石油大学 土木建筑工程学院,黑龙江 大庆 163318; 2.燕山大学 城市固废无害化协同处理及利用河北省工程研究中心,河北 秦皇岛 066004; 3.深圳市国艺园林建设有限公司研发中心,广东 深圳 518040)
开裂是影响混凝土耐久性的重要因素[1],弹性模量对混凝土开裂具有重要影响. GB/T 50081—2019《混凝土物理力学性能试验方法标准》中采用应力-应变方法测试混凝土的弹性模量[2],但对于混凝土从初凝到应用应力-应变方法进行测试这段时间(本文定义为超早期),尚无明确的测试方法. 混凝土超早期弹性模量对其早期开裂产生重要影响,也是水泥基材料数值模拟所需的重要力学参数[3],引起了国内外研究者的较大兴趣.
水泥基材料超早期弹性模量分为动弹性模量和静弹性模量[4-6]. Reinhardt 等[7]采用超声波速法测试装置,通过纵横波计算水泥基材料超早期的动弹性模量. Azenha 等[8]提出了1 种通过共振频率演变得到动弹性模量的测试方法. 静弹性模量测试法的受力与工程实际更为接近[9]. 因超早期水泥基材料不能够拆模,无法直接由应力-应变方法测得其弹性模量[10]. Delsaute 等[11]利用压力机和引伸计,测得混凝土浇筑7 h 后的弹性模量. Staquet等[12]将混凝土浇筑于狗骨形水平模具内进行水平加载,测得混凝土浇筑8 h 后的静弹性模量[13].
一些学者采用纳米压痕法研究水泥基材料的力学行为[14]. 江俊达等[15]建立了1种微观断裂韧度的计算方法.魏亚等[16]表征了净浆微观结构力学性能. 刘东旭等[17]证明了采用宏观压入法研究金属材料弹模的可行性.
本文讨论了采用压入法测试混凝土超早期弹性模量的可能性,以期为水泥基材料超早期力学性能的研究提供一种简单、高效的测试方法.
1 压入法基本原理
1.1 压入法基本公式
ISO 14577-1: 2015 《Metallic materials—Instrumented indentation test for hardness and materials parameters—Part 1: Test method》按压入深度h和载荷P,将压入法分为:纳米范畴,h≤200 nm;显微范畴,P<2 N、h>200 nm;宏观范畴,2 N≤P≤30 kN. 宏观压入试验借助传感器,记录压头在加载-卸载过程中的P-h曲线. 对该曲线的分析普遍采用Oliver-Pharr方法[18],此方法基于接触力学理论可以得到材料的弹性模量. 加载过程中试件产生弹性变形和塑性变形,卸载过程是弹性变形的恢复过程,最终的残余变形是无法恢复的塑性变形,使试件表面形成压痕. 对卸载曲线进行分析,得到材料的弹性模量. 选取卸载曲线上部的40%进行拟合,得到式(1).
式中:hf为残余压入深度;B和m为拟合参数.
对式(1)进行求导,可得:
式中:S为接触刚度;hmax为最大压入深度.
压头接触深度ho&p的计算式为:
式中:ε为压头形状参数,对于圆锥形压头,ε=0.73;对于球锥形压头,ε=0.75.Pmax为最大压入载荷.
根据接触力学与弹性力学求得接触刚度S与折合弹性模量Er的关系,其计算式为:
式中:β为压头的形状参数,对于轴对称压头,β=1;A为刚性压头的接触面积;E和ν分别为测试材料的弹性模量和泊松比;Ei和νi分别为压头的弹性模量和泊松比.
需要说明的是,本研究属于压入法的宏观测试,可认为压头的制作误差与磨损的影响相对较小,故接触面积不必修正,近似为压头与试件材料接触的投影面积.
1.2 压入法的适用条件
压入法主要用于金属材料. 基于弹性接触理论,公认的压入法基本假设为[19]:(1)均匀、各向同性的材料;(2)压入凹陷的变形模式,即周围材料随压头下沉而低于初始试件表面;(3)试件表面为平面,可忽略粗糙度影响;(4)材料尺寸远大于压入深度,可忽略边界效应的影响;(5)试样无徐变和松弛,可忽略时间因素的影响.
2 可行性研究
2.1 试件尺寸设计
相比水泥石和砂浆,混凝土中因粗骨料的存在,其具有明显的不均匀性. 为减小尺寸效应的影响,通过数值模拟方法设计混凝土试件尺寸,以满足基本假设中条件(4)的要求[20-21].
本文选用有限元软件Abaqus 进行仿真分析,研究试件尺寸对压入行为的影响,以确定合理的压入试件尺寸. 控制压入深度不变,改变试件半径和厚度,分析压入荷载的差异. 考虑到所使用的钢制圆锥压头和圆柱体混凝土试件均为旋转轴对称体,建立轴对称模型. 压头选用30°球锥压头,钢制压头的弹性模量为200 GPa,泊松比为0.30. 假定混凝土为线弹性体,其超早期弹性模量为300 MPa、泊松比为0.35. 接触类型选择面-面接触,接触属性的切向行为设定为无摩擦,法向行为设定为硬接触. 边界条件为:试件对称轴被赋予轴对称边界;试件底面约束轴向位移,即相当于将试件置于刚性底座上. 由于压入试验本质上是非线性接触问题,所以选取适合用于接触分析的C4X4R(四节点双线性缩减积分带沙漏控制的四边形)单元,单元形状选为四边形. 控制hmax为5 mm,并 将 试 件 半 径R保 持 为hmax的20 倍(100 mm).试件底部为固定端,不受外力,得出不同厚度H试件的最大压入荷载Pmax.
试件厚度与最大压入深度的比值H/hmax对压入行为的影响如表1 所示.由表1 可知:(1)随着H/hmax的降低,Fmax逐渐增大. 这是因为当试件厚度小到一定程度时,应力非均匀区域的前沿将直接进入试件底部的刚性底座,导致压入荷载偏高.(2)当H/hmax为5.0~10.0 时,荷载相对误差偏大,尤其是H/hmax降低到7.5 时,其已达20%左右. 模拟结果显示,厚度不同的混凝土上表面为达到同样的压入变形,厚度越大,混凝土表层变形范围越大,压入影响面越大. 这说明对于混凝土超早期压入试件,并非试件厚度越大越好. 综上可知,当H/hmax为20.0~50.0 时,H取为150 mm 较为理想.
控制hmax为5 mm、H为150 mm,建模并设计试件半径. 试件半径与最大压入深度的比值R/hmax对压入行为的影响如表2 所示. 由表2 可知:随着R/hmax的降低,Fmax逐渐减小. 这是因为当R/hmax小于某一界限后,应力非均匀区域内的材料受到四周材料的约束越来越小,使得试件的压入刚度下降,故压入荷载偏低,当R/hmax为20 时,相对误差的绝对值不足2.0%;当R/hmax降低到10 时,相对误差的绝对值达到8.0%. 据此可知,R/hmax大于20 为宜. 由于试件半径R的逐步减小,导致混凝土上表面的变形量越来越大,因此试件半径R不可过小. 综合选定单个压入试件半径R为100 mm.

表2 试件半径与最大压入深度的比值对压入行为的影响Table 2 Influence of ratio of specimen radius to maximum indentation depth on indentation behavior
为便于试验且兼顾经济性,将模具设计成半径为300 mm、高度为150 mm 的圆柱形模具,模具材料选为PVC 材质. 每个试件以圆心为原点,环向间距200 mm 均匀打点,模具尺寸及压入位置如图1 所示. 图1 显示:试件上表面共压入7 个点,适用假设条件(4)材料尺寸远大于压入深度,可忽略边界效应的影响的要求;同时为适用假设条件(5)试样无徐变和松弛,可忽略时间因素的影响,考虑到载荷的时间效应,超早期水泥基材料有徐变特性,会产生徐变和松弛,参考前期水泥石超早期压入法[22],将压入时间设计为1 min. 压头形式对水泥基材料也会有较大影响,需要进行压头优选试验. 为保证压入法基本假设中接触面无摩擦,混凝土在振动台上振捣1.5 min后,用抹刀将试件上表面抹平至近似镜面状态,以满足假设条件(3)的要求. 对振捣抹平后的混凝土上表面,采用钢尺轻轻划破,碰触至下方有粗骨料位置时,测量砂浆层厚度,若该厚度在1~2 mm 左右,说明振捣没有过量,满足假设条件(1)要求. 经压入试验验证,混凝土超早期压痕满足假设条件(2)的凹陷变形模式.

图1 模具尺寸及压入位置Fig.1 Mold size and press-in position(size:mm)
2.2 原材料
原材料选用秦皇岛浅野P·O 42.5R 普通硅酸盐水泥、秦皇岛热电厂Ⅱ级粉煤灰和自来水、细度模数为2.7 的中砂、粒径为5~20 mm 的玄武岩碎石. 水泥和粉煤灰的化学组成和比表面积如表3 所示. 混凝土的配合比见表4.

表3 水泥和粉煤灰的化学组成和比表面积Table 3 Chemical compositions and specific surface areas of cement and fly ash

表4 混凝土的配合比Table 4 Mix proportions of concretes
2.3 试验仪器
试验仪器为WDW3100 型电子万能试验机(载荷传感器量程为±100 kN,载荷测量精度为±0.5)、千分表、ZKS-100 砂浆凝结时间测定仪和XL2101B 5+静态应变仪.
2.4 压头和压入深度选择试验
考虑混凝土粗细骨料粒径的大小及特点[23-24],设计了5 组压头(30°球锥压头、30°圆锥压头、90°圆锥压头、90°球锥压头和圆柱压头),将其分别组装于WDW3100 型电子万能试验机上.不同形状压头示意图如图2 所示,其中90°圆锥压头和90°球锥压头材料为合金钢40Cr,弹性模量为202 GPa,泊松比为0.3. 为增大压头硬度,所有压头均经830~860 ℃油淬处理,其洛氏硬度达55 以上.
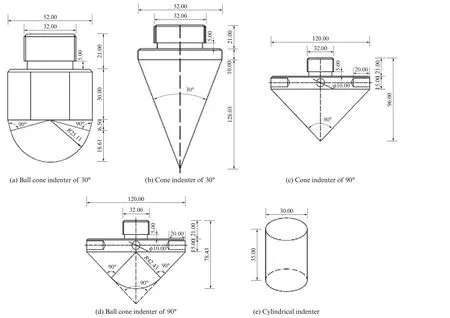
图2 不同形状压头示意图Fig.2 Sketch maps of indenters with different shapes(size:mm)
为保证压入时间相同,采用多台压力机并用不同压头同时测试混凝土超早期试件[25]. 按照GB/T 50081—2019 中混凝土弹性模量静力受压测试方法,采用千分表和WDW-50 微控电子万能试验机测试试件的弹性模量,弹性模量值取同一测试时间点3 组试件的平均值. 按照GB/T 50080—2016《普通混凝土拌合物性能试验方法标准》,测试混凝土的初凝时间和终凝时间. 采用压力试验机及静态应变仪,根据GB/T 50081—2019 得到混凝土浇筑12 h时的泊松比. 因不可压缩材料的泊松比为0.5,故假设混凝土初凝前泊松比为0.5,由内插法求出试件各时间点的泊松比值.
2.4.1 压入深度的确定
将压入时间设为1 min[25],对不同压头和不同压入深度进行测试. 试验发现采用30°圆锥压头和圆柱压头的混凝土超早期载荷-位移(P-Δ)曲线不稳定,可能与压头过尖或过平有关,故舍弃. 针对初凝时间t0为4 h的C-0.46混凝土试件,采用压入深度为8、5 mm的90°圆锥压头,测得的载荷-位移曲线如图3 所示.
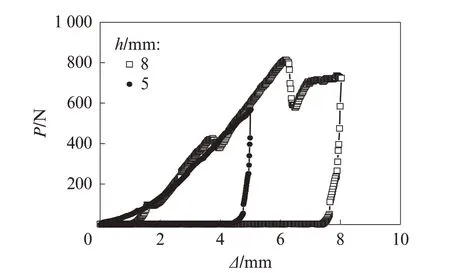
图3 采用90°圆锥压头测得的C-0.46 混凝土试件的荷载-位移曲线Fig.3 Load-displacement curves of C-0.46 concrete specimen with cone indenter of 90°
由图3 可见,当压力深度为8 mm 时,C-0.46 混凝土试件的压入荷载-位移曲线波动较大,压入困难且不稳定,说明压入深度不宜超过5 mm.
不同压头和不同压入深度试件的弹性模量曲线如图4 所示. 图4 显示,采用压入深度5 mm 的30°球锥压头测得的弹性模量值与传统应力-应变法[2]测试结果最为接近. 故本试验将混凝土超早期压入法试验的压入深度选为5 mm,加载速率选为5 mm/min.
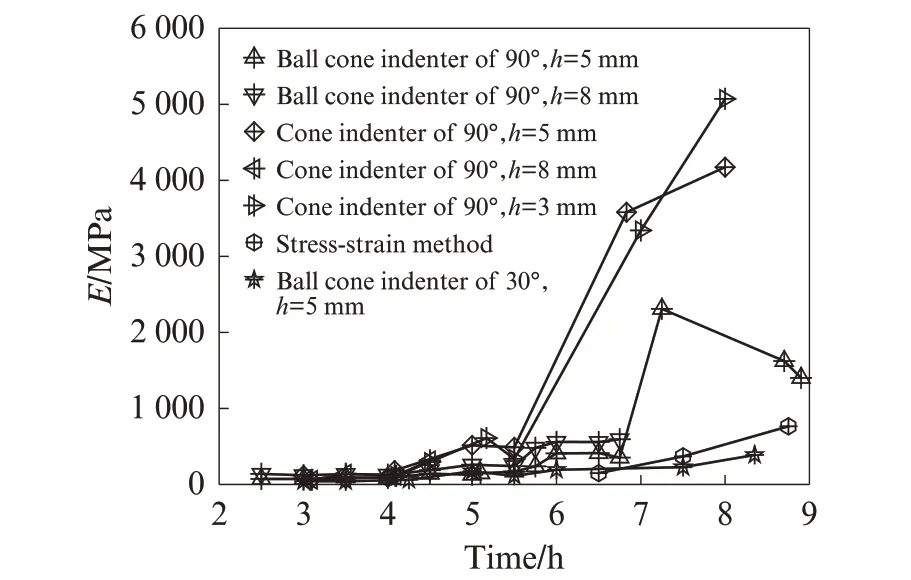
图4 不同压头和不同压入深度的弹性模量曲线Fig.4 Elastic modulus at different indenters and indentation depths
2.4.2 压头的确定
采用与传统应力-应变方法测试结果接近的3 组压头——90°圆锥压头、30°球锥压头和90°球锥压头,分别以5 mm/min 的加载速率,对C-0.48 混凝土试件进行压入法试验,其弹性模量曲线见图5. 由图5 可见,采用30°球锥压头压入5 mm 的弹性模量曲线与传统应力-应变法弹性模量曲线吻合最好,故选择30°球锥压头作为混凝土在超早期压入法测试的压头. 从混凝土拌和物中筛出砂浆,用贯入阻力法测定其初凝时间t0与终凝时间te[26].
3 试验验证
针对不同粉煤灰掺量、水胶比和初凝时间的混凝土试件,采用优选后的加载速率5 mm/min 和30°球锥压头,进行压入法试验[27]. 将压入法测得的混凝土超早期弹性模量值与传统应力-应变法、超声波法测得的弹性模量值相比较,来验证压入法的有效性.
3.1 配合比验证试验
分别选用水胶比0.42、0.44 和0.46,制备混凝土试件进行压入法测试,并与对应的传统应力-应变方法进行对比,结果见图6. 图6 显示:采用压入法与传统应力-应变方法测得的混凝土超早期弹性模量的误差在20%以内;随着水胶比的增大,试件的初凝时间随之延长,超早期弹性模量曲线更加平缓.
3.2 超声波法验证试验
参考C-0.46 混凝土试件的初凝时间测试试验,将混凝土中5 mm 以上的粗骨料筛除,参照现有超声波测试方法,采用康科瑞NM-4A 非金属超声波检测分析仪,测试剩余砂浆的纵横波波速. 其中横波(Vs)测试主频为100 kHz,试件长200 mm;纵波(Vp)测试主频为50 kHz,试件长25 mm. 根据纵横波测试结果求得C-0.46 混凝土试件是动弹性模量值[28].比较传统应力-应变法、压入法和超声波法得到的C-0.46 混凝土试件的弹性模量曲线如图7 所示.
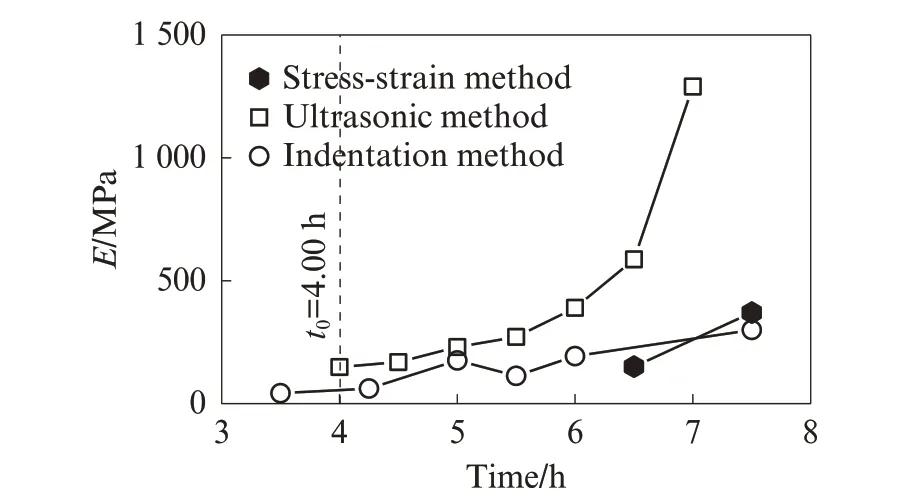
图7 C-0.46 混凝土试件的弹性模量曲线Fig.7 Elastic modulus curves of C-0.46 concrete specimen
由图7 可见:采用超声波法测得的动弹性模量值,高于采用压入法测得的静弹性模量值;特别是5.5 h 后,超声波法测试结果大幅高于压入法测试结果. 这可能是超声波法测试结果受力方式不同所致.以上动、静弹性模量测试结果显示,各曲线趋势符合水泥基材料动、静弹性模量规律,验证了压入法的可行性.
4 混凝土超早期弹性模量预测
混凝土在初凝之前,由于水泥基材料没有固化,还具有流动性和可塑性,其弹性模量值接近于0[29].将弹性模量为0 MPa 时所对应的时间设为初凝时间,据此,提出1 种混凝土超早期弹性模量的预测方法. 测试初凝时间和采用传统应力-应变法拆模后最早可测时间点的弹性模量值,通过此2 点数值所在直线对在超早期任意时间的弹性模量进行预测.分别对水胶比为0.38、0.42、0.44、0.46、0.48 的混凝土试件和水胶比为0.44 且内掺20%粉煤灰的混凝土试件的超早期弹性模量曲线进行拟合,绘制压入法测试曲线、拟合曲线和预测曲线,如图8 所示. 需要说明的是,压入法的测试起点为混凝土的初凝时刻. 图8 显示:预测曲线与压入法测试曲线、拟合曲线均较接近;各拟合曲线的相关系数分别为0.938、0.901、0.922、0.943、0.952 和0.915,拟合结果呈线性关系;取实测值中间3~5 个时间点的弹性模量值与预测曲线的数值进行对比,其相对误差均值在30%以内,说明本预测混凝土超早期弹性模量的方法可行且简便.
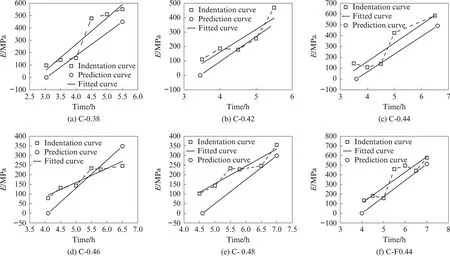
图8 各混凝土试件超早期弹性模量曲线对比Fig.8 Comparison of ultra-early elastic modulus curves of various concrete specimens
5 结论
(1)通过Abaqus 仿真分析,研究了混凝土超早期压入行为的尺度效应,得出可忽略尺寸影响的最小混凝土压入试件的尺寸(半径100 mm,厚度150 mm). 以此为依据,设计了混凝土超早期弹性模量压入法测试模具尺寸和压入位置.
(2)设计制造了5 种压头,试验表明,30° 球锥压头比90° 球锥压头更加适合于压入法测试混凝土超早期弹性模量,压入深度选为5 mm 为宜.
(3)对于不同配合比的混凝土,采用压入法与传统应力-应变方法测得的超早期弹性模量的相对误差均在20%以内,证明采用压入法测试混凝土超早期弹性模量具有可行性. 通过超声波测试混凝土的动弹性模量与压入法静弹性模量曲线趋势一致.
(4)混凝土的超早期弹性模量与时间呈线性函数关系. 基于该结论,提出1 种相对误差在30%以内的混凝土超早期弹性模量的简单预测方法——测试初凝时间并设定其弹性模量为0 MPa,以传统应力-应变方法最早测得的弹性模量为终点,通过此2 点数值所在直线对在混凝土超早期任意时间的弹性模量进行预测.
