边界条件对经典非对称相互作用晶格热化的影响

张 轩,韩雨圻,贺达海

(厦门大学 物理科学与技术学院，福建 厦门 361005)

0 引 言

非线性晶格的热化问题是一个拥有漫长历史,但仍未完全被人们所理解的课题.该类问题往往会涉及到极高的自由度,使得直接通过理论方法对其进行研究存在着巨大困难.随着计算机的诞生与发展,通过数值模拟对该问题进行研究已成为重要手段.最早的数值研究可以追溯到1955年,Fermi, Pasta, Ulam以及Tsingou (FPUT)通过研究在简谐链基础上增加非线性项后的晶格模型的正则模式能均分问题[1],实现了对非线性晶格热化问题的研究.受限于当时的计算机算力的限制,Fermi等人并未看到期望的能均分现象,而只观察到了能量在初始几个低频正则模式间来回传递的类周期性行为,即著名的FPUT回归现象,这一研究对象也被人们称为FPUT模型.之后的一系列工作表明,FPUT模型的热化过程存在两个时间尺度[2-6],在达到后一能均分时间尺度之前,存在着一个亚稳态的时间尺度,其对应于FPUT回归现象.在这一结论的基础上,人们又进一步借助数值模拟发现了FPUT模型的热化时间标度行为[5,7-8],并借助波湍流理论[9-10]给出了这一标度行为的解释.

综上可知,数值模拟在非线性晶格热化的研究中扮演着提供实验现象与验证理论预言的重要作用.不过值得注意的是,前人在数值模拟对称相互作用类FPUT模型[10]和非对称相互作用类FPUT模型[7,9]时均采用了固定边界条件,前者由于不存在热膨胀或热缩效应,如此选取边界条件可能并不会引入人为因素的干扰,与之相反的是,由于非对称相互作用会使模型存在热膨胀或热收缩性质,此时如果依然采用固定边界条件将不可避免地引入限制模型的这一性质的人为因素,这是否会导致人们错过该类模型热化过程中的一些重要特征仍未明了.基于这一考虑,本文将通过数值模拟对比不同边界条件下,相互作用势中非简谐项分别为3,4,5次的类FPUT模型以及FPUT-α-β模型的热化时间尺度同波湍流理论预测之间的差异.同时,我们将观察FPUT-α-β模型在不同边界条件下、不同时间尺度下的正则模式能量的均分情况,以了解不同边界条件对非对称相互作用晶格热化性质的影响.

1 模型及数值方法

本文所研究的是由N个仅存在最近邻非线性相互作用的原子所构成的一维单原子晶格模型,其无量纲化后的哈密顿量可写作:

(1)

其中pi和qi分别代表第i个原子的动量和其偏离自身平衡位置的位移.当上式中的相互作用势满足形式

(2)

时,人们称之为类FPUT模型,其中n为满足n≥2的整数,λ为表征模型非线性强度的参数.值得注意的是,若式(2)中参数n和λ为某些特定情况,则回到Fermi等人一开始所采用的实验模型并拥有特定的称谓,例如:若n=3,λ=α,则为FPUT-α模型;若n=4,λ=β,则为FPUT-β模型;若同时存在三次和四次项,即相互作用势满足

(3)

时,则为FPUT-α-β模型.

本文中采用的热化时间定义源自文献[7],这个定义承袭自Fermi当年的实验思路.通过计算正则模式空间的能均分时间定义了热化时间,并基于此给出了类FPUT模型的热化时间标度律.对于自由边界条件,第k个正则模式的正则坐标Qk和正则动量Pk同实空间中的坐标qi和pi转换关系为:

(4)

相应色散关系为:

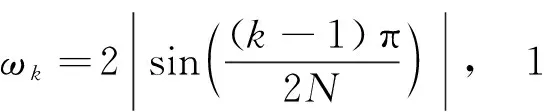
(5)

对于固定边界条件,第k个正则模式的正则坐标Qk和正则动量Pk同实空间中的坐标qi和pi转换关系为:

(6)

相应色散关系为:

(7)

注意,由于文献[11]中已证明类FPUT模型在N原子固定边界条件下同相应模型的2N+2原子周期边界条件等价,因此考虑到有限尺寸效应的影响,本文将不再单独考虑数值模拟实验中常用的周期边界条件.给定了不同边界条件下的正则模式频率以及相应变换关系后,可进一步定义正则模式能量:

(8)

正则模式空间的能均分要求时间长度T的正则模式能量时间平均

(9)

满足

(10)

其中η为时间窗口的控制参量,取值范围为[0,1),用以调整时间平均所需处理数据的量,ε=E/N表示系统的能量密度,E为系统的总能量.经数值验证,参数η的取值并不会给最终的数值结果带来影响[7].之后,引入能谱熵

(11)

来衡量不同正则模式空间能均分的程度,其中

(12)

表示第k个正则模式的能量在整个正则模式空间总能量中的占比.需要注意的是,正则模式空间中的能量只包含系统总能量E(实空间)中的简谐部分,因此它小于总能量E.这也是上述公式中分母未直接采用E的原因.在高能密度区域,这种差别会变得尤为明显,因为此时系统总能量主要存在于非简谐项中,导致正则模式空间和实空间中的总能量有较大偏差.为了减小这种偏差,在实际数值实验中会采用自洽声子理论来修正式(5)和式(7)中的ωk项,具体的细节和讨论可参考文献[12-13].不过,由于相互作用为非对称势的类FPUT模型的势能在高能密度条件下会发散,因此只有相互作用为对称势的情况才需要做这一修正.在此基础上,进一步引入有效均分自由度[7]

Q陈老师，您好！家有女宝3周岁11个月，小班。我曾经因为认字过程中她注意力不集中，或者认字不理想而发过火，造成孩子现在对学习认字特别没兴趣，她常很轻声地但带有情绪地，扭捏地或者直接说“妈妈告诉我”来应付，我该怎么做让她重新产生兴趣？

(13)

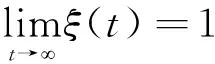
另外,如文献[7]所述,当初始条件采用低频激发时(利于观察能量在正则模式之间的传递),可对上述定义热化时间Teq的参数做出一定优化.其优化思路在于:低频激发条件下,能量最初将集中于低频区,因此真正决定系统是否热化的其实是高频区(设定为k>N/2的模式)的能均分情况.相应参数修改如下:

(14)

(15)

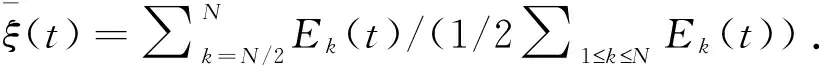
本文在自由边界条件下模拟的粒子数为N=1 024,固定边界条件下的模拟则为N=1 023,统一选择均匀激发前10%的低频模式作为初始条件,之后转换到实空间中进行数值演化,演化过程采用文献[14]中的八阶辛算法,时间步长dt会根据能量密度的不同取不同的值以避免发散,当ε≤10-2时,取步长为0.1;当10-2≤ε≤102时,取步长为0.01;当102≤ε≤105时,取步长为0.001.经验证,只要演化过程中数值不会发散,不同的步长设定并不会影响到最终的结果.另外,为了保证同前人固定边界条件下的数值模拟结果一致,本文同样取q0=qN+1=0作为晶格的固定边界.同时,由于自由边界条件的第一个正则模式代表的是晶格的整体位移,不会参与到正则模式间的能量传递,因此该正则模式在初始激发时将被越过.最后,为降低所得有效均分自由度的数值涨落,本文还将在初始均匀激发时引入24组随机均匀分布于[0,2π]的相位φk,并通过如下方式设置初始条件

(16)

以实现系综中不同系统的随机相位平均.正则模式能量的时间平均窗口控制参量η=5/6.

2 波湍流理论与类FPUT模型热化

波湍流(WT)理论是一种处理随机非线性色散波的非平衡统计力学方法.通常情况下,该理论适用于处理弱非线性的色散波,因此也被称为弱湍流理论.它最早可追溯到1929年R. Peierls在处理非线性相互作用晶体中的声子动力学时的工作[15].该理论主要发展于1965年,当时科学家V.Zakharov发现了一类新的动力学方程解[16],WT理论所应用的系统从此被归类为多自由度的强非平衡统计系统,例如湍流系统.这意味着WT理论不再局限于平衡或近平衡态的限制,从而激发了一系列新的物理应用.之后,VE.Zakharov与VS.L’vov和G.Falkovich于1994年出版了经典著作《Kolmogorov spectra of turbulence I: Wave turbulence》[17],这本书与S.Nazarenko的《Wave turbulence》[18]至今仍是希望了解WT理论的研究者的主要参考资料.需要注意的是,尽管WT理论适用于弱非线性条件,但根据前人的推导[11],我们已经知道在一维非线性晶格的热化问题中,强非线性条件下得到的结果可以看作是弱非线性条件下结果的推广.另外,由于已经有相关的研究利用WT理论推导了类FPUT模型的热化时间标度律[11,19-21],因此本文将不再详细介绍,直接给出了WT理论得到的类FPUT模型的热化时间标度律结果,具体的推导过程可参考文献[11,19].对于低能密度极限,相互作用势满足式(2)的类FPUT模型而言,根据WT理论,这类模型在热力学极限下的热化时间标度律满足:(1)若n=3,Teq∝ε-2;(2)若n≠3,Teq∝ε-(n-2).对于高能密度极限,则有:Teq∝ε-1/n.

(17)

其中λ(n)代表n次非简谐项的非线性强度参数.对于这类模型,可借鉴凝聚态物理中的多声子散射过程弛豫律Matthiessen’s rule[22]来实现预测.也就是说,其热化时间标度律将拥有

(18)

3 数值结果与讨论

在展示各类FPUT模型的热化时间数值结果之前,有必要先确认式(15)随时间的演化过程以及相应的涨落程度.具体结果如图1所示.

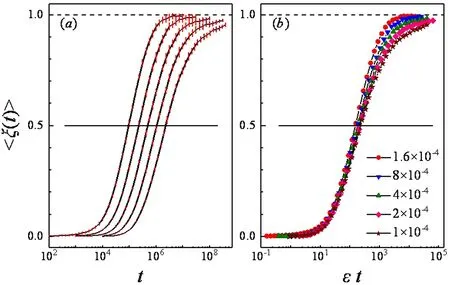
图1 (a)自由边界条件下的FPUT-α-β模型在α=-1,β=1时有效均分自由度ξ随时间的变化图(图中的曲线展示了不同能量密度条件下的ξ(t),从左至右分别为ε=1.6×10-3,8×10-4,4×10-4,2×10-4,10-4.其中的黑色曲线表示的是24组初始条件给出的系统平均值,红色误差棒则表示了相应的标准差).(b)有效均分自由度ξ(t)同ε×t之间的函数关系(图中曲线均为图(a)中的数据.两图中的黑色实线和划线均为参考线,分别代表ξ=0.5和ξ=1)

由图1(a)可知,在自由边界条件下,随着ξ→1,误差棒逐渐变长,即代表数值涨落较大,这一点在展现其标度行为的(b)图中也有所体现.相应的固定边界条件下的结果可在文献[7]中找到,除了标度行为Teq∝ε-2.25不符合图1(b)图中Teq∝ε-1的结果外,其他方面均与上图类似.需要注意的是,由于本文关注的是边界条件的选择是否会给热化时间标度律的数值结果带来影响,因此并未对有限尺寸效应的影响做更多的讨论,相应数值结果可见文献[7,10-11,19,22].

在对定义热化时间的参数ξ的标度行为和涨落有了一定认识以后,我们首先考虑的是n=4的FPUT-β模型在自由和固定边界条件下的热化时间标度律对比,如图2所示.

图2 不同边界条件下的FPUT-β模型在β=1时的热化时间对比(图中实线为斜率-0.25的参考线,划线则为斜率-2的参考线,横纵轴采用双对数坐标)

图2表明,当相互作用为对称势时,不同的边界条件的选择并不会给模型的热化时间数值模拟带来明显的差别.经过与WT理论预测的高能密度极限下的Teq∝ε-0.25进行对比,可以看到数值结果和理论吻合的很好.另外,尽管在低能密度极限下,数值模拟结果给出的Teq∝ε-2.4和WT预言的Teq∝ε-2存在一定差异,但我们认为这是有限尺寸效应所致.通过在固定边界条件下增加系统尺寸的研究(参考文献[7,19]),我们发现热化时间标度律的数值结果会随着系统尺寸的增加,逐渐趋于WT理论的预测结果,这为我们的观点提供了支撑.

接下来我们考虑相互作用为非对称势时,n=3的FPUT-α模型和n=5的类FPUT模型不同边界条件下的热化时间数值对比,分别如图3和图4所示:

图3 FPUT-α模型在α=-1时的热化时间在不同边界条件下的对比(图中黑色划线为斜率-1的参考线,黑色实线则为斜率-2的参考线,横纵轴采用双对数坐标)

图4 n=5的类FPUT模型热化时间在不同边界条件下的对比,其中非线性强度参数λ=-1(图中划线为斜率-3的参考线,横纵轴采用双对数坐标)

图3和图4表明当相互作用为非对称相互作用势时,边界条件将会给模型的热化时间带来明显的影响.有趣的是,自由边界条件下FPUT-α模型的热化时间不仅在绝对数值上和固定边界条件下的相应结果存在差异,甚至出现了违背WT理论预言的标度律Teq∝ε-1.这意味着边界条件的选择可能导致除了WT理论以外的其他能量输运机制的出现.另外,结合上文提到的Matthiessen’s rule和这里Teq(3)∝ε-1的数值结果,就解释了为何图1(b)中FPUT-α-β模型有效均分自由度ξ的标度行为同文献[7]中不同了,毕竟在低能密度条件下,非线性项中起主要作用的应该是3次项.

除此之外,我们还发现在自由边界条件下FPUT-α-β模型的热化过程不存在亚稳态,这与前人文献展示的固定边界条件下的结果不同[7].

图5(a)的结果同文献[7]的结果一致,系统的正则模式能量在时间尺度T=103,104,105上并未继续均分,即出现了亚稳态.这一结果对应于FPUT回归现象,对其最早的研究可以追溯到著名的文献[23].目前,它是少数几个在FPUT热化问题中没有争议的结论之一,并且已经有大量相关研究对其进行了讨论.然而,如图5(b)所示,自由边界条件下系统的正则模式能量一直处于均分的过程中,未能出现如固定边界条件下那样明显的亚稳态.与此同时,经验证,拥有对称相互作用的FPUT-β模型则在不同边界条件下都给出相同的结果.这些结果表明,当晶格中的相互作用存在非对称性时,一旦不再抑制由此引出的热膨胀或热收缩性质,系统将不再出现以往人们所熟知的孤立波[23]结果,正则模式之间的能量传递在一开始就是畅通的,对其做进一步探索将是非常有价值的课题.

4 总 结

本文研究了边界条件对经典非对称相互作用晶格热化的影响.通过数值模拟,我们分别对比了n=3,4,5时的类FPUT模型以及FPUT-α-β模型在不同边界条件下的热化时间标度律和WT理论的预测结果的差异,发现当相互作用为对称相互作用势时,可以忽略边界条件带来的影响,与之相对的是,对于非对称相互作用势,边界条件的选择会给热化时间带来不可忽略的影响,甚至还可能导致除WT理论以外的其他能量输运机制的出现.更进一步,我们通过数值模拟对比了自由和固定边界条件下不同时间尺度下FPUT-α-β模型正则模式能量的均分情况,发现边界条件的选择甚至会影响到亚稳态的出现.综上可知,边界条件对于非对称相互作用势而言是一个不可忽略的重要因素,对其物理机制的深入理解仍有待进一步研究.