基于响应曲面法的BGA 焊点结构参数优化设计

杨雪霞，孙勤润，张伟伟

(1.太原科技大学,太原,030024；2.东莞理工学院,东莞,523000)

0 序言

BGA 也即球栅阵列封装，该器件由于良品率高、散热好、电气性能优越而被商业厂商生产应用[1].电子产品在实际使用时，会因受到振动、热载荷作用而失效，必须进行封装可靠性测试评估提出优化方法[2].

随着BGA 的应用及环境复杂性，其热振可靠性优化成为研究热点.电子设备工作中存在热机械疲劳、振动和蠕变等各种负载，导致焊点应力集中产生裂纹贯穿焊点而破坏.其中接近55%焊点故障是热作用失效，另外近20%因振动而失效[3].针对热振载荷下IC(integrated circuit)封装因子稳健设计问题，学者们多采用DOE(design of experiment)结合FEA(finite element analysis)方法来研究改进封装结构焊点可靠性[4].如韩立帅等人[5]通过有限元模拟CSP(chip scale package)焊点在随机振动的应力应变分布，并结合响应曲面法得到了最优组合；黄春跃等人[6]借助灵敏度分析，进行数值模拟发现影响CSP 再流焊残余应力重要因素是焊点直径；Cho 等人[7]用DOE 设计结合FEA 法进行了焊点可靠性优化研究.众多研究表明焊点直径、高度、间距等因素对可靠性具有显著影响[8]，FEA 结合DOE 因子分析研究焊点可靠性有着其准确性和必要性.上述研究关于焊点结构参数对电子封装的系统优化研究不够精确和细致全面，尤其是复杂环境下的焊点几何结构参数对可靠性的显著影响仍需进一步讨论研究.

文中结合响应曲面法和有限元分析法，将3D 封装微尺度BGA 焊点作为研究对象，确定了3 个包含焊点直径、焊点高度、焊点间距几何结构参数对热振可靠性的显著性影响，进行回归分析并结合遗传算法预测了最优组合，后进行仿真验证测试.研究结果将为提高BGA 器件焊点的热振可靠性提供科学依据.

1 BGA 焊点可靠性有限元分析

1.1 三维有限元模型及边界施加

文中将选择仙童半导体公司FAN48632UC33X BGA 产品，进行热振的情况下数值模拟.将BGA 简化成PCB 板、SAC305 焊点、Si 芯片.具体尺寸为焊点直径0.25 mm，焊点高度0.24 mm，焊点间距0.4 mm，PCB 板40 mm × 40 mm × 1.8 mm，Si 芯片2.5 mm × 2.5 mm × 0.4 mm，横纵距离为5 mm.BGA 焊点用Multizone 尺寸分区方法划分，其他部分自由网格划分，网格数据统计单元质量0.87，单元数量350 126 个，节点数873 216.BGA有限元模型如图1 所示.

图1 BGA 有限元模型Fig.1 Finite element model of BGA

采用Ansys Workbench 软件进行BGA 在热振耦合下的力学行为进行有限元计算.板级BAG 封装结构中，焊点SAC305(Sn3.0Ag0.5Cu)熔点大约有217 ℃，采用粘塑性Anand 本构关系进行描述，详细参数见表1[9]，PCB 板和Si 芯片均为线弹性材料，材料性能参数见表2.边界条件为限制基板运动，对基板螺栓孔施加全约束，沿螺栓孔面垂直于PCB 板的Z轴为振动方向.

表1 SAC305 焊料的Anand 模型粘塑性材料参数Table 1 Visco-plastic parameters of Anand model for SAC305 solder joints

表2 材料性能参数Table 2 Property parameters of materials

热循环交变荷载依据《MIL-STD-883》标准，加载的热循环曲线见图2.设定的热循环参数为参考温度25 ℃，变化区间-55～ 125 ℃，高低温维持时间15 min，温变速率20 ℃/min，单周期2 880 s，截止时间11 520 s，共进行四个稳定温度循环周期.

图2 热循环温度载荷曲线Fig.2 Thermal cycle temperature load curve

随机振动条件基于《MIL-ATDNAVMAT P9492》标准的PSD 加速度功率谱曲线，如图3 所示.随机振动频率20～ 80 Hz 时，其振动量值为+3 dB/oct，对应的加速度功率谱幅值范围是0.01～0.04 g2/Hz；随机振动频率在80～ 350 Hz 时，加速度功率谱密度水平幅值为0.04 g2/Hz；随机振动频率在350～ 2 000 Hz 时，其振动量值为-3 dB/oct，对应的加速度功率谱幅值范围是0.04～ 0.01 g2/Hz.

图3 随机振动加速度功率谱密度曲线Fig.3 Random vibration PSD curve

试验所采用顺序耦合建立了热循环与随机振动之间的耦合分析流程，先进行了热循环交变载荷的分析，将前述得到的分析结果作为随机振动的载荷输入后，进行了模态分析和随机振动分析，从而得到热-随机振动耦合作用下BGA 封装结构的有限元分析结果，流程图如图4 所示.

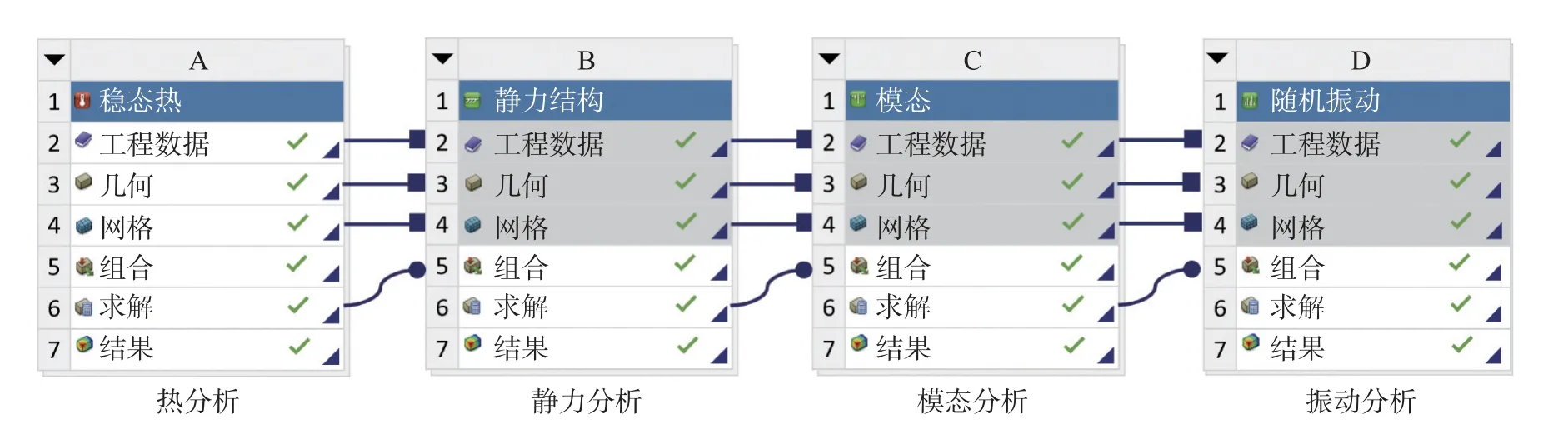
图4 热循环与随机振动耦合流程图Fig.4 Flow chart of coupling of thermal cycle and random vibration

1.2 BGA 焊点模拟结果与分析

BGA 封装结构中各个部件间的热膨胀系数及密度属性有所差异，因而在热振作用下各组分间的拉压作用承受较大的非弹性变形产生了应力集中.而在此过程中焊点阵列作为最薄弱的机械连接部分而遭破坏，因此热循环与随机振动作用下选取了挠性PCB 板上的焊点阵列作为研究对象，提取焊点等效应力云图，见图5.由图可知，焊点等效应力值阵列角点处最高，并且值向中心焊点逐渐减小；单鼓状关键焊点等效应力值由最大径向位置向PCB 板与Si 芯片接触界面处逐渐增大；最大等效应力值在芯片封装中心最远的焊点靠近PCB 板界面处，值为0.419 5 MPa，定该角焊点为关键焊点.温度致使焊点塑性下降产生低周疲劳失效，而动态振动形成交变应力使得焊点因高周疲劳发生脆性断裂裂纹，使得电子产品加快失效.

图5 焊点等效应力云图Fig.5 Equivalent stress distribution of solder joints

2 响应曲面BGA 结构参数优化

2.1 响应曲面稳健方案设计

响应曲面法主要有以下几种试验设计方案，中心复合设计、BBD(Box-Behnken)设计、D-optimal设计、均匀设计等.文中选用有简单均布性特点的BBD 设计，其根据因素水平可恰当的减少试验次数，选择芯片高度、焊点直径、焊点高度、焊点间距为控制因素，每因子取三水平，控制因素与水平因子详见表3.

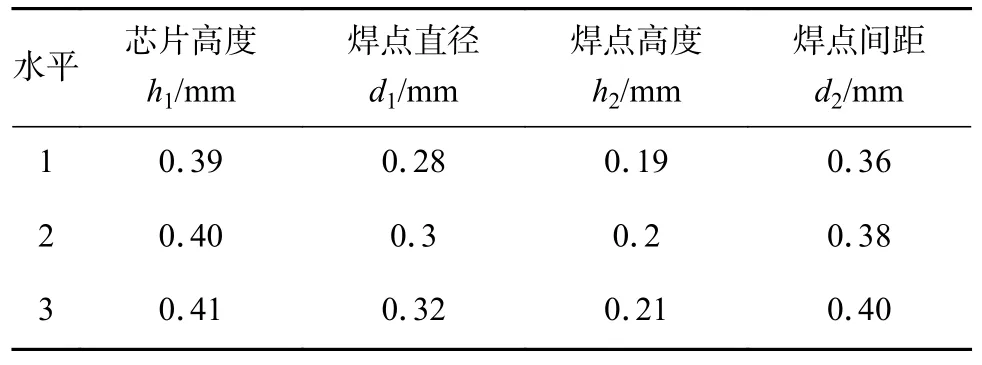
表3 控制因素及水平因子Table 3 Control factors and levels

根据BBD 设计、BGA 结构失效准则，确定了25 组以焊点等效应力作为评价焊点可靠性指标的试验方案组合，如表4 所示.

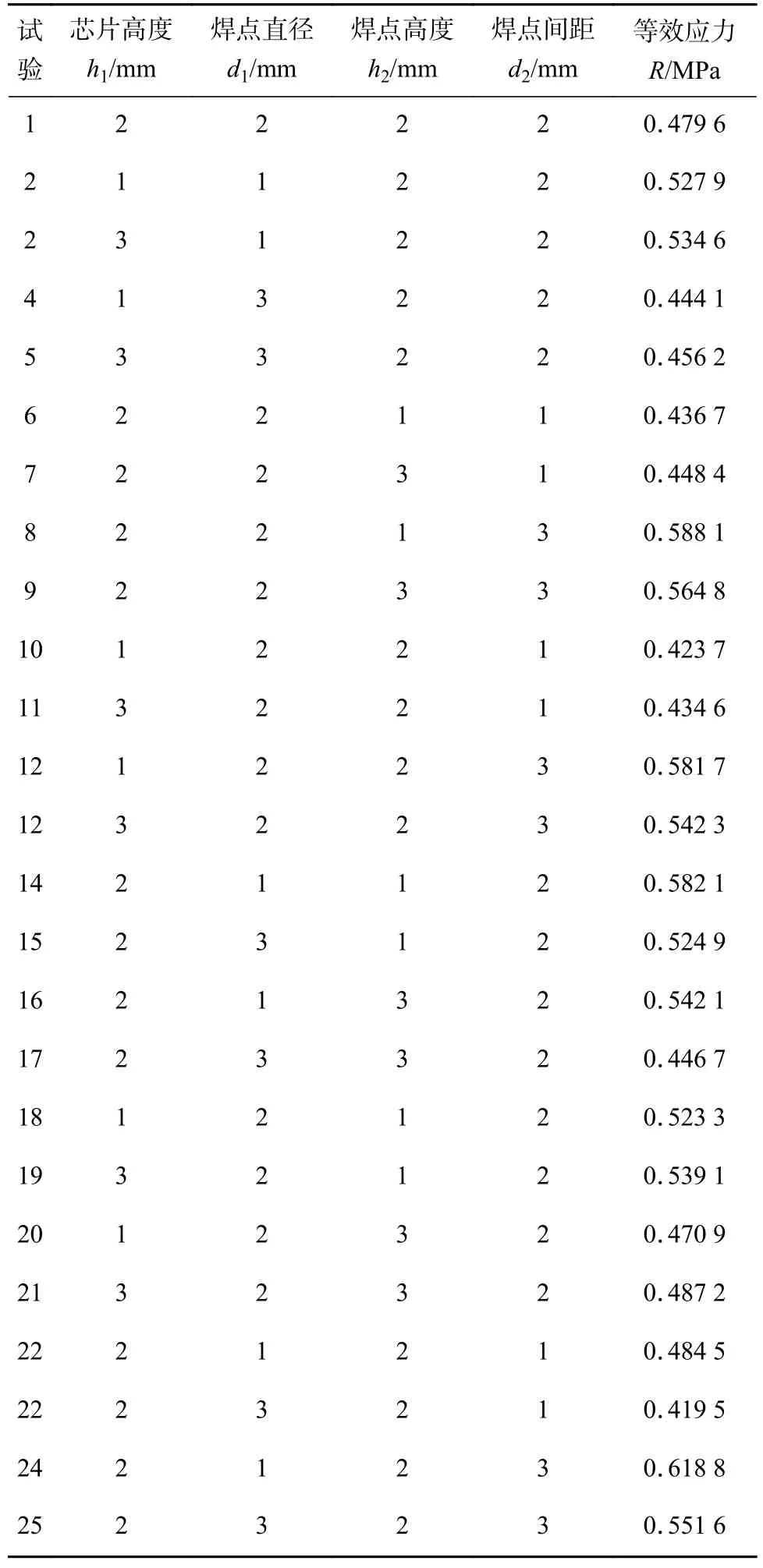
表4 BBD 试验方案及等效应力结果Table 4 BBD test scheme and equivalent stress results

2.2 回归分析

基于表4 进行数据分析并二次多元回归拟合，将芯片高度(x1)、焊点直径(x2)、焊点高度(x3)焊点间距(x4)定义为回归方程4 个自变量，将等效应力值(y)作因变量，得初次回归式，即

对上述得到的回归拟合方程进行方差分析，确定显著性因素及回归相关评价，筛选前方差显著性验证见表5，筛选前回归方程分析结果见表6.

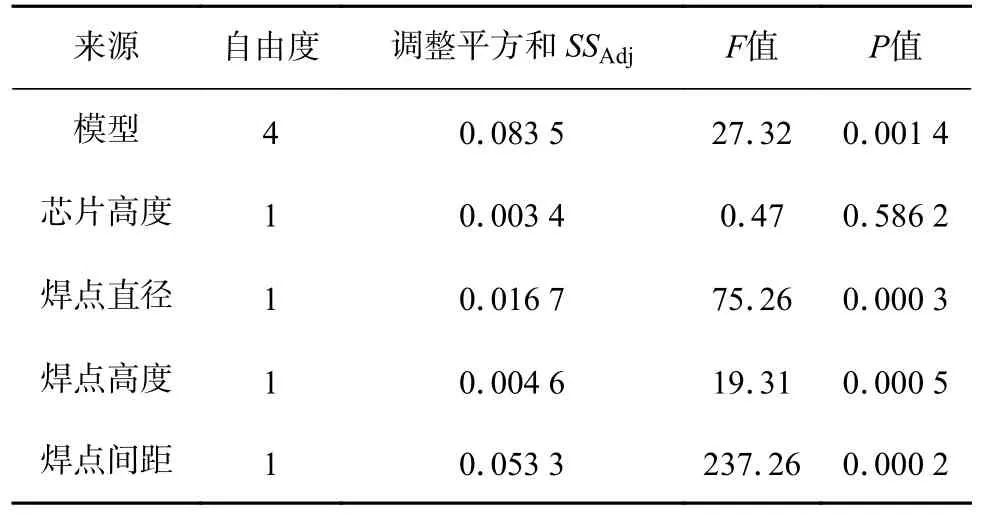
表5 筛选前方差显著性验证Table 5 Analysis of variance significance before screening

表6 筛选前回归方程分析Table 6 Analysis of regression equation before screening

在置信水平95%的情况下，当P值小于0.05 时，则拒绝原假设优化目标与各因子没有相互影响.由表5 可知，模型总体是显著的，但芯片高度的P值为0.586 2 ＞ 0.05 并不显著.由表6 可知，初次回归方程系数、调整系数和预测系数(0.921 4、0.902 6 和0.817 6)均有较好拟合度但并不足够好，可再进行细致分析.

因此剔除不显著的因子及交互项因子后，重新进行二次回归方程拟合，以期望达到更好拟合程度，进行更准确的预测.更新后得到回归方程，即

同样的，对式(2)进行了方差显著性验证和回归拟合程度好坏的评价，筛选后方差显著性验证见表7，筛选后回归方程分析结果见表8.

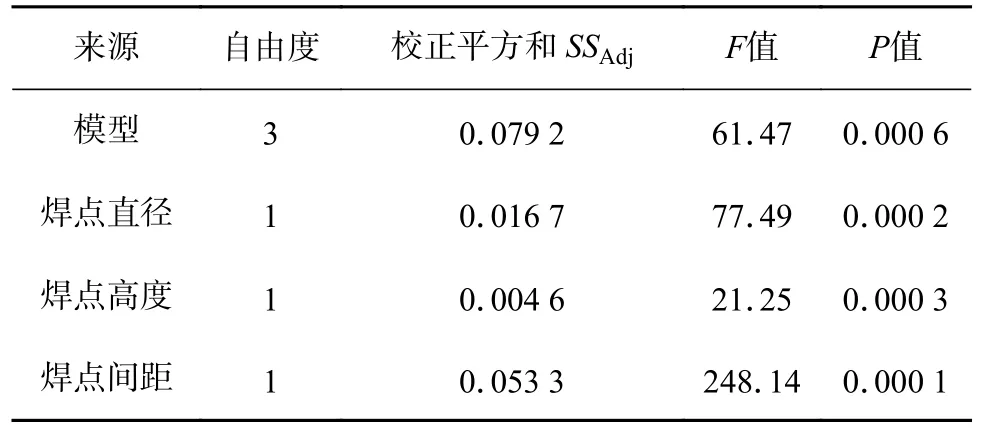
表7 筛选后方差显著性验证Table 7 Analysis of variance significance after screening

表8 筛选后回归方程分析Table 8 Analysis of regression equation after screening

由表7 可知，在筛选非显著性因子后，置信水平95%的条件下，模型总体P值0.000 6 ＜ 0.001 4，较之前更加显著，BGA 焊点等效应力与焊点直径、焊点高度、焊点间距及他们平方项间均显著(P＜0.05)，且显著性提高.由表8 可知，筛选后回归方程系数、调整系数和预测系数(0.948 6、0.933 1 和0.899 3)较之前初次拟合度效果更加优良与提升，可进行下一步的研究工作.

为避免方差显著性分析的偶然性，我们还绘制了在置信水平95%(α=0.05)，确定了因子显著水平的标准化效应Pareto 图和正态图，如图6、图7所示.

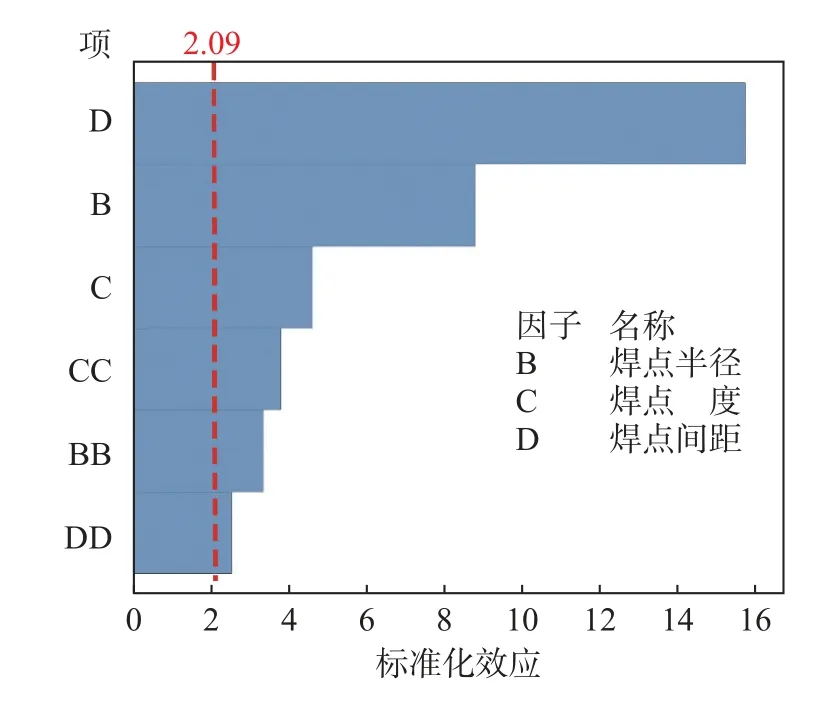
图6 因子标准化效应的Pareto 图Fig.6 Pareto plot of normalization effects

图7 因子标准化效应正态图Fig.7 Normal plot of standardized effects

标准化效应的Pareto 图可确定效应的量值和重要性.在图6 中可以看出在标准化效应超过2.09 时，则说明因子项在 α=0.05下是显著的，这再次验证了方差显著性分析的准确性.但Pareto 图只知效应的绝对值，无法确定增大或者减小因子对等效应力响应的影响，因此进一步可用标准化正态图确定.

标准化效应正态概率图可确定效应的量值、方向和重要性.在图7 中可看出，离0 较远的因子效应在统计意义上更显著，图中因子均显著且影响权重次序为焊点间距＞焊点高度＞焊点直径；这是由于间距直接影响了温度的扩散.其中因子焊点直径和焊点高度对等效应力是负效应，而因子焊点间距对等效应力响应是正效应，据倾斜紫色直线清晰得到.

2.3 遗传算法优化

遗传算法(Genetic Algorithm)由Holland 教授提出的一种搜索进化方法.依据上节筛选了非显著因子后得式(2)，再运用遗传算法对热振作用下等效应力最低为目标进行参数优化.

根据表3 设约束如下0 .28 ≤x2≤0.32；0.19 ≤x3≤0.21；0.36 ≤x4≤0.40 (x2焊点直径，x3焊点高度，x4焊点间距)，个体变量数为3，种群个体数60，变异0.2，迭代次数为175 次，迭代175 次后的适应度函数种群均值最优解变化见图8.

图8 目标函数种群均值和最优解变化Fig.8 Mean and optimal change of objective function

此时输出BGA 焊点各结构参数最优水平如下为x2=0.28、x3=0.20、x4=0.40，由图8 可知最优解为0.379 9 MPa，与表4 最小值0.419 5 MPa 相比减小了0.039 6 MPa，达到了BGA 优化目的.

其预测准确性仍需进行仿真验证，在其他条件不变情况下，将优化焊点直径0.28 mm，焊点高度0.20 mm，焊点间距0.40 mm 重新进行有限元仿真验证，得到最优水平组合焊点等效应力图见图9.

图9 最优水平组合焊点等效应力图Fig.9 Equivalent stress diagram of optimal combination

由图9 可知，BGA 焊点热振耦合过程中等效应力值为0.369 5 MPa，与遗传算法优化的预测值0.379 9 MPa 相比，预测误差为2.73%；与表4 中等效应力最小值0.419 5 MPa 相比减小了11.92%；由此证明了该优化方法得到的焊点内应力有所减小.

3 结论

(1)仿真研究表明最大等效应力值在芯片封装中心最远的焊点靠近PCB 板界面处，且影响BGA 焊点可靠性主要因素是焊点间距，这是由于间距直接影响了温度的扩散.

(2)采用响应曲面—遗传算法结合得到BGA 焊点参数组合为焊点直径0.28 mm，焊点高度0.20 mm，焊点间距0.40 mm，仿真验证该组合在热振耦合加载时BGA 焊点所承受应力减小，实现了优化目的.