重卡驾驶舱的装配偏差分析与优化

2023-12-09张殿平马春辉孙芮信思勇高芷芃张雷雷

机械工程师 2023年11期

张殿平，马春辉，孙芮，信思勇，高芷芃，张雷雷

（1.中国重汽集团济南动力有限公司，济南 250220；2.上海交通大学机械与动力工程学院，上海 200240）

0 引言

随着电商物流领域的迅猛发展重型卡车市场呈现出供不应求的局面。重卡制造企业在提升产能的同时也更加关注整车质量、产品性能和生产成本等关键因素。驾驶舱作为重卡的核心组成部分，其装配制造质量对整车质量、生产周期和服役年限等都具有重要影响。因此，驾驶舱制造过程中装配质量的提升受到车企的关注。

装配质量主要受零部件质量、装配工艺、安装顺序等因素的制约[1]。为此，研究人员通常采用智能化算法搭建信息化平台实现产品装配质量的提前预测[2-3]。陈资等[4]结合遗传算法和支持向量机构建了数控机床装配质量预测模型，其预测精度优于BP神经网络和常规支持向量机模型。方喜峰等[5]结合粒子群算法和支持向量机构建船用柴油机装配质量预测模型，在提高预测精度的同时缩短了运算时间。董海等[6]提出的XGBoost模型能够精准预测多级制造系统中车身装配质量。臧阳阳等[7]提出了基于变量选择和概率神经网络的质量预测模型，解决了装配过程中影响因素繁多、数据不平衡的问题。刘银华等[8]基于偏最小二乘回归算法构建车身多工位装配偏差预测模型，实现关键特征的合格率预测与零部件质量的优化控制。

当实际制造过程中出现不合格产品时，需要及时进行根本原因的诊断并进行决策优化。常用的诊断方法包括模式匹配、统计估计和智能算法等[9]。Khodaygan等[10]提出了基于贝叶斯模型的装配公差优化方法，在保证可靠性的基础上评估装配质量。Fu等[11]提出一种基于事件触发的白车身装配质量前馈预测控制方法，实现精度的在线控制，降低夹具调整频率。袁博等[12]通过文本挖掘技术从历史数据中提取信息，利用推荐算法辅助人工进行质量问题诊断，实现装配过程的提质增效。郭允明等[13]提出随机Kriging代理模型对装配过程工艺参数进行优化控制，减少了工艺不确定性对装配精度的影响。胡晓磊等[14]结合机理模型和数据驱动模型构建汽车前轮定位参数的预测模型，通过公差优化设计降低了定位参数超差率。朱永国等[15]基于熵权法和灰色综合关联度构建装配质量偏差源诊断模型，可在小样本条件下实现精确诊断。

综上所述，智能算法和优化方法在装配质量的预测、诊断及控制中表现出色。然而，上述研究主要停留在理论认证阶段，且主要针对小型乘用车或商用车，对于重卡驾驶舱的多材料装配质量研究较为欠缺。本文利用仿真软件搭建重卡驾驶舱装配过程机理模型，采用优化算法实现工艺参数与安装顺序的改进，并完成真实车型的落地应用。

1 仿真模型

1.1 驾驶舱装配过程与问题描述

本文以某重卡车型驾驶舱的装配过程开展研究。驾驶舱的装配结构及分解结构如图1所示。

车门、翼子板及导风板等零部件或总成件通过“一面两销”的定位方式与白车身进行焊接，装配顺序如表1所示。

表1 驾驶舱结构装配顺序

整车试制阶段发现：1）导风板与前面罩的间隙过大，左、右两侧皆呈现A字形缝隙，如图2（a）所示；2）导风板与前门面差呈现上小下大趋势，且下侧面差过大，如图2（b）所示。针对左侧导风板装配后与匹配件的间隙、面差不满足要求的问题，本文将开展根本原因诊断、装配工艺和安装顺序优化等研究。

图2 整车试制过程间隙、面差问题表现

1.2 驾驶舱装配仿真流程

使用3DCS软件对驾驶舱装配过程进行仿真，仿真流程如图3所示。

图3 驾驶舱装配仿真流程图

步骤1。将带有结构树的驾驶舱三维数模导入软件中，通过零部件偏移的方式创建装配与分解两种场景，并在分解场景下开始建模。

步骤2。根据GD&T图样中的标注分别为每个零件创建基准面与基准孔，并在对手件的相应位置创建特征。

步骤3。依照焊接工艺流程图建立零部件/总成件之间的装配关系，主要基于“3-2-1定位”原理实现零件的约束，多个件装配时需严格按照装配顺序创建装配关系，不能颠倒。

步骤4。根据GD&T图样中的孔、面公差为零件添加尺寸公差和位置公差，尤其是孔、销的直径及装配面的轮廓度等。同时为装配过程添加孔-销浮动等影响。

步骤5。根据测点文件或DTS在数模的相应位置添加测量点特征，并建立测量操作，实现驾驶舱装配后各关键位置的间隙和面差输出。

步骤6。通过点击装配按钮模拟驾驶舱的真实装配过程，点击分析按钮实现基于Monte Carlo方法的三维尺寸链分析，输出步骤5中关键位置的尺寸超差情况及造成超差的原因和贡献率。

步骤7。当步骤6中尺寸分析的结果不满足要求时，至步骤8，否则至步骤9。

步骤8。通过修改零件结构、形位公差、装配顺序等手段对工艺方案进行改进，并将改进后的结果反馈至步骤2，在现有的仿真模型上进行修改。

步骤9。输出形位公差分配结果、装配工艺流程等信息，用于指导实际生产过程中的质量控制。

以上装配过程是建立在所有零件都是刚性的假设条件下，且不受自重、焊接等因素的影响而发生变形。所有零件及装配工艺参数都假设服从正态分布，且认为偏差落在±3σ以内即为合格产品。

2 仿真结果与优化分析

2.1 驾驶舱装配仿真结果

仿真过程中针对导风板与其对手件的间隙和面差进行测量，测量位置如图4所示。

图4 关键测量点的间隙、面差

共设置了4组间隙、面差共8个测量点，Gap_1/Flush_1与Gap_2/Flush_2两组测量点位于导风板与前面罩的匹配处，Gap_3/Flush_3与Gap_4/Flush_4两组测量点位于导风板与左前门的匹配处。经过2000次的Monte Carlo仿真计算，4组测量点的三维尺寸偏差分析结果输出如表2所示。

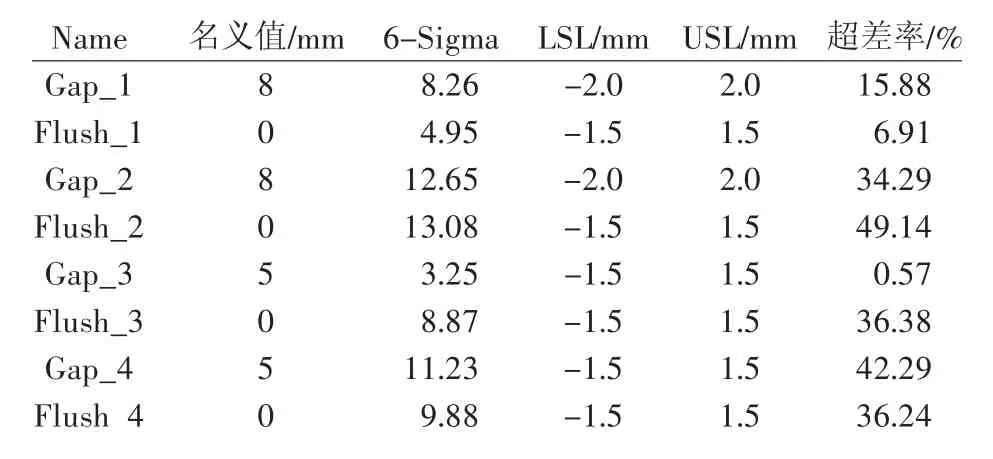
表2 测量点尺寸分析结果

结合历史工程实际经验，认为仿真结果中超差率大于10%则不能接受。从表2中可以看出，只有Flush_1和Gap_3测量点满足要求，其余测量点均与要求相差甚远。Gap_2/Flush_2的6-Sigma皆大于Gap_1/Flush_1，Gap_4/Flush_4的6-Sigma皆大于Gap_3/Flush_3，因此与试制过程中出现的问题相同，说明仿真过程基本符合实际情况。仿真结果同时输出了每个测点超差的影响因素及其贡献率，如表3所示。

表3 测量点尺寸超差的影响因素及贡献率

表3 中，Move15 代表导风板支架安装至BIW的过程，Move16 代表左导风板安装至前挡左下饰板支架1的过程。装配过程对尺寸偏差的影响主要由孔销浮动造成，其余影响因素则是由公差设置造成最终尺寸偏差。

2.2 优化分析

从2.1节的分析结果可以看出，Move16_左导风板安装至前挡左下饰板支架1的装配过程影响了6个测点的尺寸偏差，且贡献度均较大。因此，从Move16装配过程的孔销浮动开展分析。导风板的装配过程如图5所示，4-way定位销设置在前挡左下饰板支架1上，2-way定位销设置在导风板支架上，定位销的直径皆为6 mm。

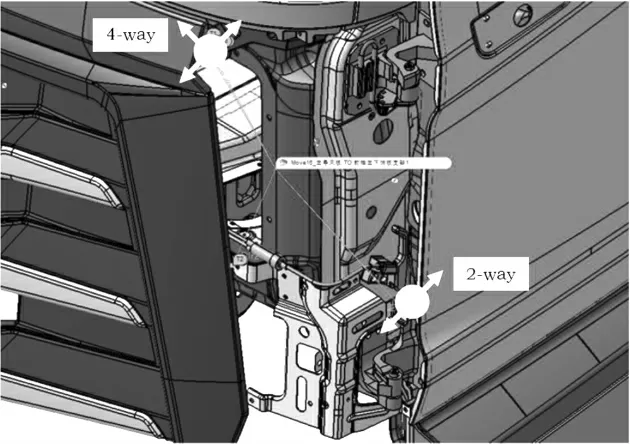
图5 导风板装配过程示意图

与定位销相对应的导风板定位孔直径为10 mm，定位孔直径远大于定位销直径，导致装配过程Y向的孔销浮动量过大，因此造成最终的尺寸偏差。根据工程经验，定位孔直径应比定位销直径大0.5 mm才能保证正常孔销浮动量，为此在仿真模型中将定位孔的直径修改为6.5 mm。Move15_导风板支架安装至BIW过程中的孔销浮动问题与Move16相同。修改定位孔直径后尺寸分析结果如表4所示。

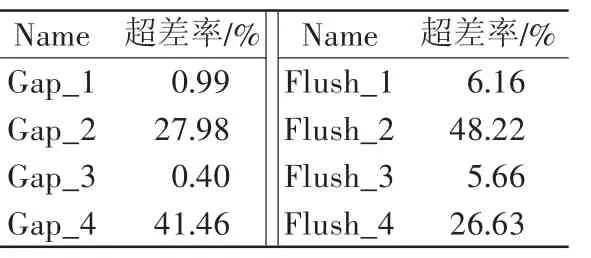
表4 修改结构后尺寸分析结果

从表4中可以看出，Gap_1/Flush_1和Gap_3/Flush_3的尺寸分析结果已经满足工程需求，然而Gap_2/Flush_2和Gap_4/Flush_4的超差率依然较大。因此，需要通过公差的优化分配来实现尺寸偏差的控制。

综合尺寸分析结果、影响因素及其贡献率，本文选取“X1：导风板支架安装孔位置度”、“X2：导风板支架安装面轮廓度”、“X3：前挡下饰板支架安装面轮廓度”、“X4：前面罩总成安装面轮廓度”和“X5：前面罩总成安装螺母孔位置度”这5个变量作为影响因素，“Y1：Gap_2”、“Y2：Flush_2”、“Y3：Gap_4”和“Y4：Flush_4”的超差率作为因变量。其中，X{X1，X2，X3，X4，X5}的公差取值范围是[1.8, 3.0]，Y{Y1，Y2，Y3，Y4，}贡献率的优化结果应小于10%。基于蒙特卡罗方法随机生成影响因素的公差，并以此进行模拟仿真分析，共获得500组对应数据。在三维空间中，影响因素与超差率之间是非线性关系，因此本文基于BP神经网络实现影响因素与超差率之间的关联关系建模。

影响因素的公差优化过程中，公差值越小则超差率越小，但同时零部件的制造成本也随之增加[8]。为此，本文引入制造成本与BP神经网络拟合的超差率共同作为目标函数。采用模拟退火算法对目标函数进行求解，实现影响因素的公差优化分配，优化结果如表5所示。

根据表5的公差优化结果，修改仿真模型中影响因素的公差设置，并重新实现仿真过程，公差优化后的尺寸分析结果如表6所示。