基于烟花算法的BP 神经网络预测含根土抗剪强度
2023-12-08刘俊麟郝勇刘春艳邵严丁琅
刘俊麟,郝勇*,刘春艳,邵严,丁琅
(1. 长江大学城市建设学院,湖北 荆州 434000;2. 长江大学园艺园林学院,湖北 荆州 434000)
生态护坡,是利用植物根系对岩土体的加固效应对边坡表层土壤进行防护,在达到固土目的的同时还能对环境进行保护,是一种绿色环保的防护方式[1]。抗剪强度是用以反映土壤抵抗变形破坏能力的指标,探究含根土抗剪强度可以较为直观地反映生态护坡效应中植物根系对土壤的加固效果。考虑到近年来鄂西山区在农业发展中越来越重视茶叶产业,而茶场的建设需要清理山坡原有植被,研究茶树(Camellia sinensis)含根土抗剪强度对分析茶树根系固土效果以及与其他林草植被固土效果做对比具有重要的实际意义。
前期许多学者对含根土的抗剪强度进行了各种研究。杨永红等[2]通过室内直剪试验,比较了4 种类型植被覆盖的情况下土壤抗剪强度的大小,发现表层植被增加抗剪强度的效果显著;刘小燕等[3]研究了花岗岩残积土条件下狗牙根(Cynodon dactylon)根土复合体表明复合体的抗剪强度因为植物根系的存在有极为显著的提高;吕晶等[4]通过测试比较天然草本、人工草本的根系与土壤复合体的抗剪强度,发现植物根系可以显著提高土壤的抗剪强度;陈昌富等[5]利用室内三轴直剪试验的方法研究了狗尾草(Setaria viridis)根-土复合体强度特性,其结果表明根-土复合体的强度和抵抗变形的能力较素土有显著的提高;卢立霞等[6]研究了嘉陵江江岸的12 种优势须根系草本植物,结果表明12 种须根系植物均显著提高了土体抗剪特性。冯国建等[7]对无根土体和含芦竹(Arundo donax)和狗牙根两种植物根系的根-土复合体试样进行直接剪切试验的结果表明,根-土复合体的抗剪强度高于无根土,根-土复合体的黏聚力显著升高,但内摩擦角变化不显著。左小锋等[8]分析研究冻融循环作用对土壤抗剪强度的影响,表明土壤抗剪强度与团聚体平均重量直径呈正相关。王润泽等[9]通过测定根系指标、根-土复合体抗剪和抗冲性能研究得出了不同土层香根草(Chrysopogon zizanioides)和马唐(Digitaria sanguinalis)的根系扫描参数(根表面积、根体积等)与根-土复合体的抗剪强度呈正相关。
目前的研究多以剪切试验的方法对含根土抗剪强度的增量进行量化,用来评价植物根系对土体强度的提升效果[10-11]。但是这种方法过于依赖室内剪切试验,同时由于土体本身的不稳定性,往往会出现数据离散性较大的情况,无法直观地观察到其中的规律。而人工神经网络作为人工智能的一个重要分支,具有较为强大的数据分析能力和非线性预测能力,对根土复合体抗剪强度这种受结构特性影响大、离散性较大的问题具有很好的处理能力。同时,前期党维维等[12]、金坎辉等[13]、江巍等[14]、黄发明等[15]在采用人工智能方法预测各类岩土体抗剪强度及稳定性方面做了许多有益探索。
因此,本研究在前人研究成果的基础上,通过进行直剪试验、团聚试验以及根系分形分析试验等获取相关参数,建立合适的BP(back propagation)神经网络模型预测含根土的抗剪强度可以有效地解决根土复合体抗剪强度的非线性和离散性问题。同时为解决BP 神经网络容易出现局部极值、运算速率过慢等问题,引入了烟花算法(fireworks algorithm, FWA)对传统BP 神经网络进行优化,使其更具有实用价值。
1 材料与方法
1.1 试验材料
2022 年5 月,为获取足量且扰动相对较小的含根土样,在9 个种植袋(90 cm×30 cm×30 cm)中人工种植茶树苗,为期3 个月,种植土取自宜昌市远安县茶场(111.642° E;31.0599° N)原状土。在大棚内对茶树苗进行培养(图1),保证茶树苗根系已经充分成长后用环刀进行取样,于2022 年8 月进行室内试验。取样时,用环刀取直剪土样,并在环刀的周围取60 g 土样作为团聚试验土样。另外,取部分含根土样以及完整茶树根系进行分形分析,每组试验3 次重复。

图1 茶树苗生长环境Fig.1 Growth environment of tea samplings
1.2 直剪试验
直剪试验共进行了70 组(含根土60 组,素土10组),采用标准环刀取土(图2),取出的环刀土尽量在不影响土壤本身湿度及结构稳定性的情况下带回实验室开展直剪试验(直剪仪,ZJ-1 型应变控制式直剪仪,河北),试验过程中,剪切速率宜控制在0.8~1.2 mm·min-1(即手轮保持4~6 r·min-1),当百分表读数达到稳定或有显著后退时,停止转动。将环刀土在不同的竖向荷载作用下进行剪切,记录不同读数[16-20],根据公式计算土的剪应力(τ,kPa) :

图2 直剪试验土样和团聚试验水桶Fig. 2 Soil sample of direct shear test and water breaker of agglomeration test
式中:R为百分表(0~10 mm,上海)读数(变形值0.01 mm);m为量力环系数,本试验取值为1.587;A为试验土样剪切截面面积,本试验取标准环刀截面积30 cm2;10 为单位换算系数。
数据处理时,以剪应力(τ)为纵坐标,竖向应力(σ)为横坐标,绘制σ-τ关系曲线,曲线的截距即为土壤的黏聚力,曲线斜率即为土壤的内摩擦角,根据库仑定律可表示为:
式中:c为土壤黏聚力(soil cohesion, kPa);φ为土壤内摩擦角(°)。
1.3 团聚试验
团聚试验即沙维诺夫筛分试验,共进行了120 组(含根土60 组,素土60 组)。在土壤保持其原形态下采用沙维诺夫干筛法[21],以探究根系对土体机械稳定的团聚性能的影响;采用沙维诺夫湿筛法[22],以探究根系对土体水稳定团聚体性能的影响,进而考察土体的抗冲刷侵蚀能力。本研究中分别采用干筛法和湿筛法对含根土的团聚效果进行研究。
取60 g 风干样本置于套筛中,手动摇筛至各级筛上的团聚颗粒不再下降为止,然后收集各级筛上的土样,称重并计算各级团聚体重量占风干土样总重量的百分数。取30 g 土样作为湿筛样本置于套筛中,缓慢放入水桶(图2),保证水桶中的水位高出套筛顶部1 cm 左右,随即手动上下微摆30 min 后取出,待水分稍干后洗出各级筛中的团粒,放入烘箱烘干后称量。
根据测算,团聚体粒径大小为>2 mm、1~2 mm、0.5~1 mm、0.25~0.5 mm 以及≤0.25 mm,R0.25表征土壤结构稳定性的大团聚体(>0.25 mm)含量,根据不同区间的重量、平均直径和质量百分数等计算可以得到土壤团聚体平均重量直径(mean weight-diameter, MWD)、几何平均直径(geometric mean-diameter, GMD)[23-24]和土壤分形维数(soil fractal dimension,Dd)。MWD 和GMD 是反映土壤团聚体大小分布状况的指标,其值越大,表征土壤团聚度越高,土壤稳定性越好。Dd用于表征团聚体数量对土壤稳定性的影响,数值越大,团聚体的分散度越大,土壤稳定性越差。
式中:di为各粒级的平均直径(mm);Wi为各粒级的重量占比百分数(%);dmax为最大团聚体的平均直径(mm);M(r<di)为粒径小于di累计的重量(g);MT为样本总重量(g)。
1.4 分形分析
分形分析试验共进行了60 组。将环刀内的土样整体取出,放入容器中加水浸泡几分钟,使土壤软化脱落,再用缓慢流动的水冲刷根系,使黏性较大的土颗粒完全脱落,直至根系被完全洗净。而后利用EPSON 根系分析仪(J221A, 印度尼西亚)对处理完的茶树根系进行扫描(图3),并使用WinRHIZO(2007v)根系分析软件提取根系形态相关参数(图3)。取得的参数包括根系的分叉数、根系交叉数、根长、根表面积、平均直径、体积等。

图3 茶树根系和部分含根土样分形扫描Fig.3 Fractal scan of tea tree roots and some root-bearing soil sample
1.5 神经网络方法
1.5.1 BP 神经网络算法 人工神经网络(artificial neural network, ANN)是一种由多个神经元组成、模拟人类大脑、用于解决非线性大规模自适应的数据处理智能仿生模型[25]。其中,BP 神经网络由输入层、隐含层和输出层三部分组成(图4)。从本质上来讲,BP 神经网络将大量样本的输入和输出问题变成了一个非线性的优化问题,通过加入权值和隐含层等可调节参数提升了整个系统的灵活度和精确度,保证系统在多次迭代下误差输出最小。因此BP 神经网络在含根土的抗剪强度的预测上有着较强的实用性。

图4 典型的BP 神经网络结构Fig.4 Typical BP neural network structure
传统的BP 神经网络工作流程如下:1)对BP 神经网络的各项参数进行初始化,权值和阈值取较小的随机数;2)输入训练样本;3)计算神经元处理后各层的输出值;4)计算输出层和隐含层的误差情况,若误差达到要求,则进行下一步骤,否则返回第2 步;5)从输出层反向计算到第一个隐含层,不断调整各神经元网络连接的权值和阈值,使误差不断地趋于减小;6)不断重复以上第3~5 步,直到误差达到要求,结束训练。
但是,传统的BP 神经网络存在许多局限性,例如:在计算过程中容易陷入局部极值,在计算某些问题时训练速度十分缓慢,训练时新样本加入会导致存在遗忘旧样本的趋势等。
1.5.2 FWA-BP 神经网络算法实现 烟花算法是由北京大学教授谭营老师等从看到烟花爆炸中得到启发,所提出的一种新型群体智能优化算法[26-29],工作原理较为简单,并且具有强大的全局搜索能力和较快的收敛速度,因此被广泛应用。烟花算法对BP 神经网络的优化可以采取以下步骤:1)种群初始化。烟花在某一个特定的区域(Ω)内随机形成烟花初始位置,即xi∈Ω。2)计算适应度。步骤1 中的每一个烟花个体都对应一个BP 神经网络,将训练样本输入网络以后,将网络的期望值与预测值的误差作为适应度函数(均方误差mean squared error,MSE或均方根误差root mean square error,RMSE),并根据计算所得的数值初始化核心烟花算子的爆炸幅度半径。
式中:di为期望值;yi为神经网络的预测值。
3)产生爆炸火花。烟花算法产生的火花有两种,分别为“爆炸火花”和“变异火花”,产生火花的个数以及演化的爆炸范围由以下公式决定:
式中:Si代表第i(i=1, 2,…,N)个烟花所产生的火花数目;Ai代表第i个烟花的爆炸幅度范围区间,存在一定的条件限制,即将要爆炸的火花会在该范围内随机移动到一个新位置但是不能超越这个范围界限;a,b,c均为常数,a用来限制产生的火花总数,b用来限制火花爆炸幅度的大小,c为一个非常小的常数以避免出现分母等于零的现象,默认值为2.2204×10-16;Ymax与Ymin分别表示当前火花群体中适应度值最好与最差个体所对应的适应度值;f(xi)为个体xi的适应度值。在计算出烟花的爆炸幅度以后,需要计算出烟花在爆炸范围内的位移:
式中:rand(0,Ai)表示在烟花爆炸幅度Ai内均匀且随机生成的数值。
4)选择策略。烟花算法的选择策略是要在经过爆炸和变异的火花中选出种群中最优的火花作为下一代的烟花,经常采用欧氏距离来测量任意两个个体之间的距离:
式中:R(xi)表示任意个体xi与种群中其他个体之间的距离总和;K表示经过爆炸和变异产生火花位置的集合;d(xi,xj)表示种群中任意两个个体之间的欧氏距离。采用轮盘赌的方式选择个体,则个体被选中的概率为:
5)条件判断。若满足条件则停止循环,不满足条件则返回步骤3。
本研究利用烟花算法对BP 神经网络进行优化,将BP 网络的初始权值和阈值长度作为烟花种群初始化数据,将BP 神经网络的期望值与预测值之间的误差作为适应度函数,不断对权值和阈值进行优化,直到满足条件后再返回到BP 神经网络中根据优化后的权值和阈值对输入数据进行训练及预测。
1.5.3 模型误差评价 利用3 种统计检验方法[30-32]即均方根误差(root mean square error, RMSE)、平均绝对误差(mean absolute error, MAE)和平均绝对百分比误差(mean absolute percentage error, MAPE)验证FWA-BP模型精度。
RMSE 是均方根误差,表示实际值与预测值之间的平方偏差与测试集数量之比的平方根。RMSE 的值越小,模型的误差越小,准确性也就越高。当实际值与预测值完全一致时,证明这个模型是一个完美的模型。
式中:xai是期望值;xpi是预测值;n为测试样本数量,下同。
MAE 是平均绝对误差,表示平均值的绝对值与所有预测值的偏差和算术平均值。通过以下方法对模型进行评估:MAE 的值越小,模型的误差越小,模型的准确性越高。与RMSE 类似,当期望值与预测值完全相同时,模型是一个完美的模型。
MAPE 是平均绝对百分比误差,是度量平均预测值与实际值之间的相对误差。采用MAE 值越小,模型误差越小,精度越高的准则对模型进行评价。与RMSE 和MAE 相似,当实际值与预测值一致时,模型是一个理想的模型。
1.5.4 模型参数选取 综合以上论述,通过不同的试验得到了数个不同的参数,本研究选取R0.25、MWD、GMD、Dd、根表面积、平均直径6 个参数作为神经网络的输入层节点,黏聚力(c)作为神经网络的输出层节点。训练数据及预测数据见表1 和表2。

表1 训练样本Table 1 Training samples

表2 预测样本Table 2 Prediction samples
1.5.5 神经网络结构确定 本研究采用3 层的BP 网络。输入层和输出层的节点数一般由所研究的实际问题决定,故本研究采用输入层6 个,输出层为1 个节点。对于隐含层的节点数目前没有固定的公式可用,经查阅相关文献,本研究总结了主要的3 种计算方法:FangfaGorman 理论神经元数目(S)与输入参数(N)的关系为S=log2N;Kolmogorov 理论神经元数目(S)与输入参数(N)的关系为S=2N+1;一种经验公式神经元数目(S)、输入参数(N)和输出参数(M)之间的关系为S=sqrt(0.43MN+0.12NN+2.54M+0.77N+0.35)+0.51。
本研究中BP 网络的输入参数为6,输出参数为1,采用以上3 种公式计算得到的结果分别为3、13、4,在本研究中用这3 个隐含层神经元数分别进行预测,并对其结果进行误差分析。
隐含层和输出层的传递函数分别为S 型正切函数和对数函数,网络训练函数为“traingdx”,在学习过程中采用梯度下降法,学习速率为自适应。
1.6 数据处理
采用Excel 进行数据的基础处理以及分析对比;采用IBM SPSS Statistics 23 软件对试验获得的影响含根土抗剪强度的各因素进行相关性分析;采用Origin 2021 制图。
2 结果与分析
2.1 试验结果分析
2.1.1 直剪试验结果分析 黏聚力和内摩擦角是反映土抗剪强度的主要参数。在直剪试验中发现,含根土的黏聚力平均值为12.7 kPa,素土黏聚力平均值为9.2 kPa,含根土的黏聚力较素土提升约38%,但对于内摩擦角平均值,含根土为10.2°,素土为10.3°,两者相差较小(表3)。由此判断本试验中茶树根系对土的抗剪强度的提升主要表现在含根土黏聚力的大小变化,与内摩擦角的大小无关。因此,在本研究中主要讨论黏聚力作为评价含根土抗剪强度的主要参数。

表3 直剪试验数据统计Table 3 Statistical statistics of direct shear test
2.1.2 团聚试验分析 当采用干筛法进行试验时,含根土中>2 mm 颗粒含量为36.84%,<0.25 mm 的颗粒含量为5.61%(表4),整体来看,颗粒含量与颗粒粒径大小呈正相关,对素土而言则刚好相反,颗粒含量与颗粒粒径大小呈负相关,这说明根系对维持土体机械稳定性能有较好的效果。采用湿筛法进行试验时,含根土各级颗粒含量相差不大,均在20%左右,素土颗粒含量与颗粒粒径大小呈负相关,反映出植物根系对土体的抗冲刷性能也有较大提升。

表4 团聚试验颗粒统计Table 4 Statistical result of particles in agglomeration test
2.1.3 各因素相关性分析 根据统计学原理[11],使用SPSS 分析软件对影响含根土抗剪强度的各因素进行相关性分析,得到各因素与黏聚力之间的相关系数(表5)。

表5 各因素与黏聚力的相关系数Table 5 Correlation coefficient between each factor and cohesion
从以上定性分析可以看出(表5),各因素对含根土的抗剪强度均有一定的影响;从定量的计算可知,单个因素均与含根土的黏聚力有一定的相关性,但相关性不大。这说明各因素与黏聚力即抗剪强度之间不是简单的线性相关,而是存在一种非线性的、隐性的关系。利用神经网络的高度非线性映射关系可以较好地反映含根土抗剪强度与各因素之间的这种关系。
2.2 不同神经元数目预测结果分析
根据前文所述,隐含层神经元数目是根据3 种不同的公式计算得到,为确定最合适的隐含层神经元数量,分别对应用不同隐含层神经元的神经网络进行计算预测(表6)。当隐含层神经元数目分别为3、4、13 时,BP 网络对应的最大误差分别为20.18%,19.64%,11.12%(表6),同时注意到当隐含层神经元数量为3、4 时,BP 神经网络的预测值大部分都为12.5~12.6,反映到图中就是一条趋近于直线的平缓曲线,表现出BP 网络容易陷入寻找局部最优解的特点;PSO-BP 网络对应的最大误差为17.20%,17.50%,9.06%,FWA-BP 网络对应的最大误差为14.83%,18.76%,7.44%,可以看出,当隐含层神经元数目为13 时,3 种网络对应的最大相对误差最小,此时神经网络的预测精度最高,即对于本次神经网络应用Kolmogorov 理论计算隐含层神经元数量是最合理的。所以,本研究中神经网络隐含层神经元数量定为13。

表6 不同隐含层神经元预测结果对比Table 6 Comparison of prediction results of different hidden layer neurons
2.3 模型预测结果分析
本研究采用FWA-BP 神经网络对含根土的抗剪强度进行预测,同时将PSO-BP 神经网络作为对照组进行计算。其中,FWA 的初始种群数目设置为20,高斯变异与爆炸的烟花数目为5;参数a、b大小设定为50、40,爆炸幅度不设置下限;模型运行次数设为20 次,函数评估次数设为40 万次,维数大小为30。确定各神经网络结构后,将训练样本以及测试样本输入到神经网络中进行训练和预测。
BP 神经网络预测值与期望值最大相对误差为11.12%,此时的预测值为11.7 kPa,对应的期望值为10.5 kPa;PSO-BP 神经网络预测值与期望值最大相对误差为9.06%,此时的预测值为11.5 kPa,对应的期望值为10.5 kPa;而FWA-BP 神经网络预测值与期望值的最大误差仅为7.44%,此时的预测值为11.3 kPa,对应的期望值也是10.5 kPa(图5,图6 和表7)。相同的期望值,不同神经网络得到的预测值也不同,其中,FWA-BP 神经网络的误差最小,精度最高。对比平均相对误差数值,FWA-BP 神经网络仅为1.96%,是3 种神经网络中数值最小的一种。同时对比曲线图,FWA-BP 网络预测值的曲线是最贴合期望值的。证明了本研究选取训练参数的合理性以及利用烟花算法优化BP 神经网络用以预测含根土抗剪强度的可行性。
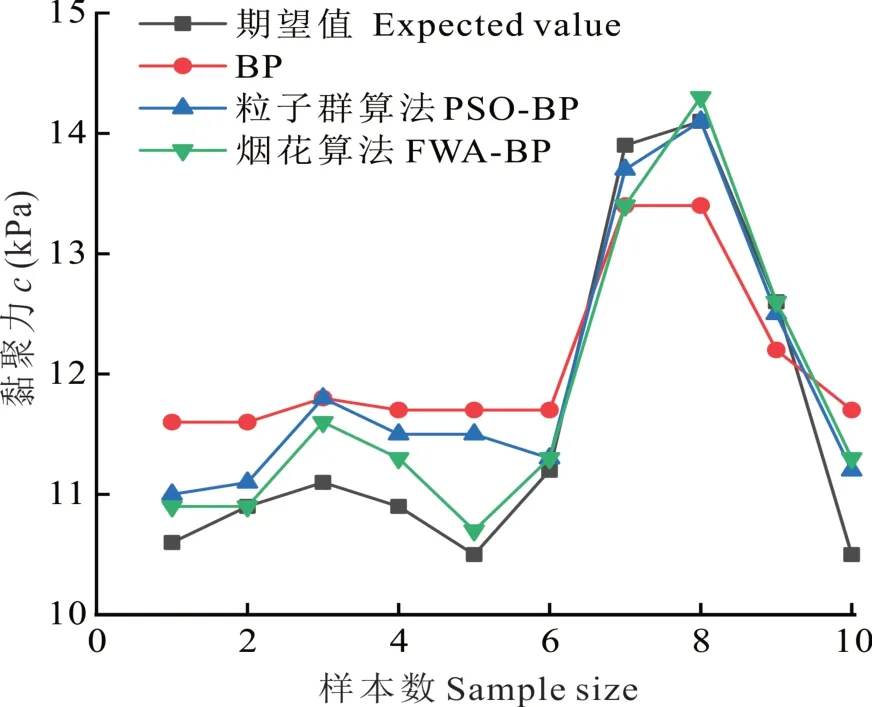
图5 3 种神经网络预测值与期望值对比Fig. 5 Comparison of predicted values and expected values of three neural networks

图6 3 种神经网络预测值与期望值误差对比Fig. 6 Comparison of predicted value and expected value error of three neural networks
2.4 不同模型误差分析
为进一步检验模型精度,计算求得3 种模型的误差数值(表8)。对于均方根误差(RMSE),FWA-BP 模型的数值最小,BP 模型和PSO-BP 模型的数值较大且两者相差较小(表8);对于平均绝对误差(MAE)和平均绝对百分比误差(MAPE),BP、PSO-BP以及FWA-BP 模型依次减小,即3 种模型的预测精度依次提高,这与前文预测结果相对应。证明应用FWA-BP神经网络预测含根土的抗剪强度是比较可行的。
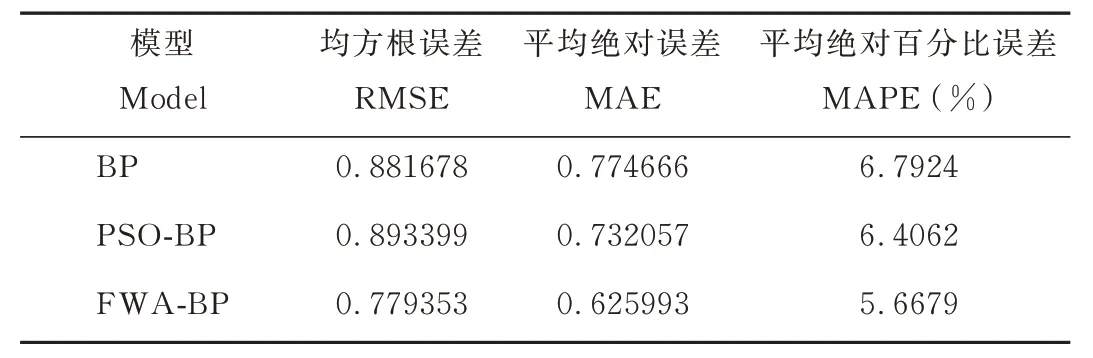
表8 不同模型的统计检验Table 8 Statistical tests of different models
3 结论
通过直剪试验、团聚试验和分形分析试验,本研究选取R0.25、MWD、GMD、Dd、根表面积、平均直径6 个参数作为神经网络的输入层节点,选取黏聚力作为神经网络的输出层节点,而后应用神经网络进行计算预测,得到结论如下:1)通过直剪试验分析发现,含根土的抗剪强度相比较素土提升了约38%,提升幅度较大。同时,对团聚试验结果进行分析,发现茶树根系对维持土体的机械稳定性能有着较大作用,可以提高土体的抗冲刷性能。研究结果为综合评价茶树根系固土效果以及与其他林草植被固土效果做对比提供了一定的参考数据。2)通过计算对比,选用隐含层神经元数量为13 时,各神经网络预测值与期望值的误差最小,最大误差分别为11.12%(BP)、9.06%(PSO-BP)、7.44%(FWA-BP);3)不同的神经网络模型对含根土的抗剪强度预测中,FWA-BP 神经网络的预测值和期望值误差最小,误差统计参数RMSE、MAE、MAPE 分别为0.779353、0.625993、5.6679%,相较于其他两种模型数值最小,证明FWA-BP 神经网络模型精度更高。应用烟花算法优化神经网络进行含根土抗剪强度预测是可行的;4)由于含根土抗剪强度的影响因素较多,本研究通过试验获取对应的参数来计算预测含根土的抗剪强度,在试验过程中,可能会受到试验方法、试验仪器等因素的影响造成一定的误差,还可能存在一定的片面性,后续研究应综合考虑土壤含水率、孔隙率、比重等多种因素,更全面地分析和研究此类问题;5)烟花算法是一种高精度、易收敛并且全局搜索能力较强的群体智能算法,在实际应用中具有很强的优越性,但目前的研究主要集中在路径规划方面,在草业科学领域和岩土领域研究相对较少,后续应该对其进行更深入研究,以期获得更多的成果。
