大体积混凝土结构温度裂缝控制方法的模拟与试验
2023-12-08王新雨
王新雨
(中铁十八局集团第三工程有限公司,河北 涿州 072750)
大体积混凝土在现代建筑中起着重要作用,尤其是在筏板基础、厚墙和大坝等大型结构的施工中[1]。混凝土在水泥水化过程中会产生大量热量,由于结构的热耗散率不同,水化热在结构中产生温升,会导致大体积混凝土核心与其表面之间的高热梯度[2-3]。如果结构中的热应力(即拉应力)超过混凝土不断发展的抗拉强度,特别是在混凝土早期强度仍在发展时,就会形成热裂纹,进而影响大体积混凝土结构,尤其是混凝土地下结构的安全性和耐久性。因此,控制混凝土温度以防止裂缝是大体积混凝土设计和施工的主要目标。为实现这一目标,通常采用的方法是降低混凝土最高温度和大体积混凝土中的温差。冷却管是降低温度峰值和梯度的有效方法之一,但这种方法成本很高,风险很大[4-5]。为了降低温度梯度,也可在大体积混凝土结构的所有表面覆盖多层薄板保温材料,以保持大体积混凝土结构内的热量,并确保其表面温度与其核心温度相差不大。但这种方法不利于降低混凝土峰值温度,如果过早拆除隔热层,可能会导致热震开裂。因此,这种加热方法通常与预冷技术相结合,以提高大体积混凝土水化热降低的效率。基于加热方法的原理,研究人员提出了一种降低大体积混凝土基础水化热的新技术,该技术可使大体积混凝土的温差和峰值最小化。其优点是在混凝土浇筑过程中,不需要2层之间的水平施工缝,从而提高了大体积混凝土的完整性。各层混凝土比例和上层厚度对大体积混凝土热性能的影响是该技术的2个重要方面。为此本文采用有限元方法进行数值模拟,并对大体积混凝土块进行了现场试验。通过与试验结果的比较,验证模拟温度场的正确性,得出层间混合比例和层厚的变化规律。
1 建模参数
本研究采用2.5 m×2.5 m×2.5 m的混凝土块进行试验,在进行现场试验之前,先确定试验混凝土块的混合料以及层厚。在Midas Civil软件中建立并分析了混凝土块的有限元模型。假定该大块混凝土块作为基础位于地基上,对此进行2次建模分析。
1.1 分析模型几何图形和输入参数
图1为大体积混凝土块的模型几何结构。由于模型及其边界条件的对称性,为了减少计算工作量,本文分析了1/4具有相应边界条件的混凝土块(见图2)。用于模型计算的参数值如表1所示。在最初的研究中,环境温度被设定为27 ℃。假设混凝土浇筑和地基温度分别为30 ℃和20 ℃。

图1 大体积混凝土块的几何结构模型
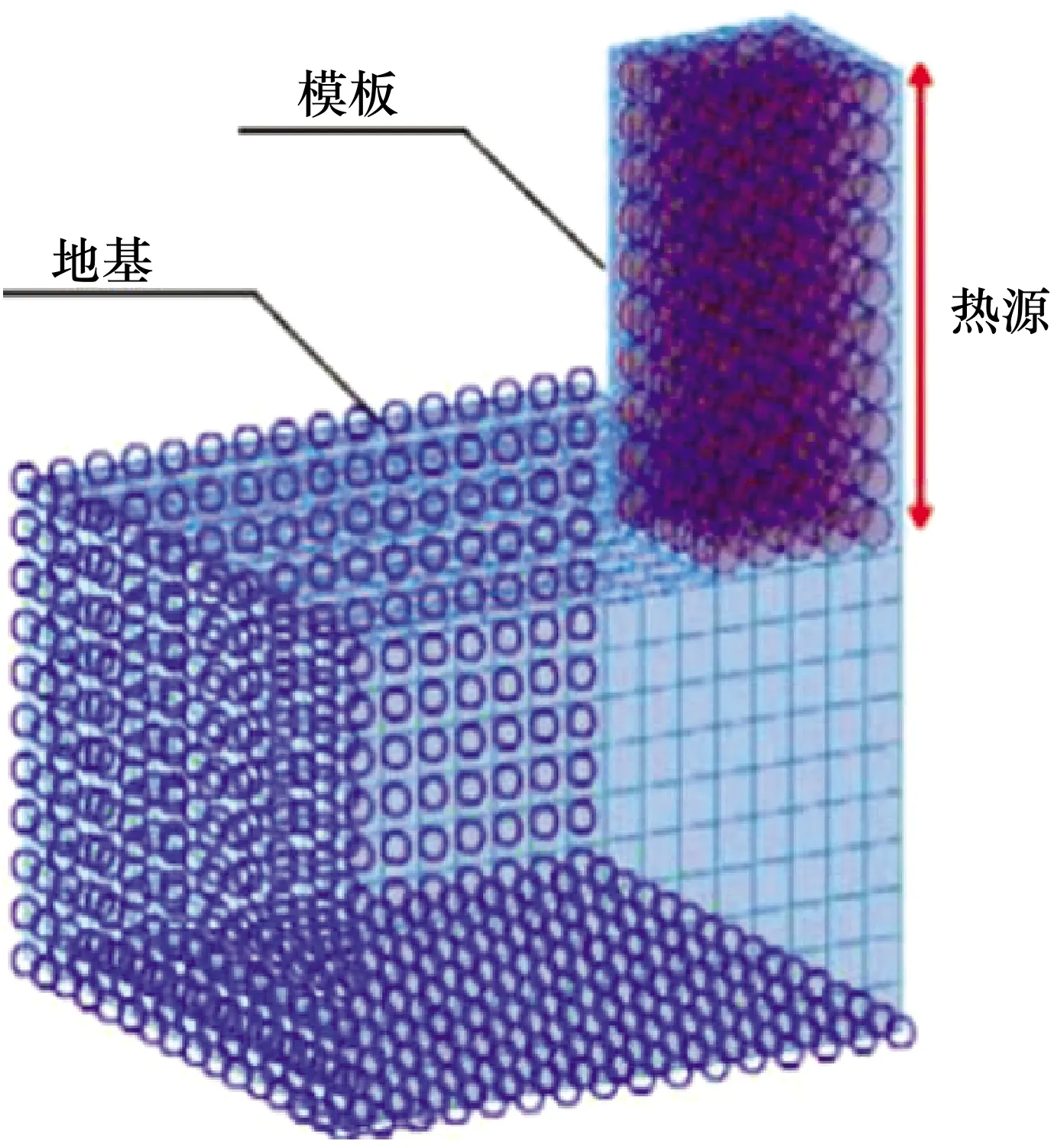
图2 1/4混凝土块模型的边界条件

表1 用于模型计算的参数
1.2 第1次分析:分析模型只有1种混凝土混合物
第1次分析的目的是在只有1种混凝土混合物的情况下测试基础的温度场,研究粉煤灰对温度场的影响。1 m3混凝土中砂、碎石、水、胶凝材料的质量分别固定为880,951,160,385 kg,按照不同的水泥/粉煤灰的配比浇筑3个试件,如表2所示。混合料中使用的水泥均为普通硅酸盐水泥,预拌混凝土的设计抗压强度均为40 MPa。

表2 1 m3混凝土胶凝材料配比 %
图3为3个试件对应的基础中心和表面的温度变化。可以看出,在浇筑混凝土后50 h,3个试件混凝土块中心的峰值温度分别为80.6,71.1,62.3 ℃,浇筑后200 h,由于散热,混凝土块中心温度逐渐下降至约40 ℃。试件1、2在温升超过70 ℃时可能导致延迟钙矾石生成(Delayed Ettingite Formation,DEF)现象的发生,会导致混凝土损坏。浇筑后50 h,3个试件的基础中心和表面之间的温差最大值分别为38.5,31.2,24.6 ℃。试件1、2在温度梯度超过25 ℃后出现热裂缝。由此可知:1)随着粉煤灰质量的增加,地基中心的峰值温度和基础中心与表面之间的温差均减小;2)试件3不会因热问题开裂,因此,使用粉煤灰替代部分水泥是控制大体积混凝土热裂缝的有效方法。
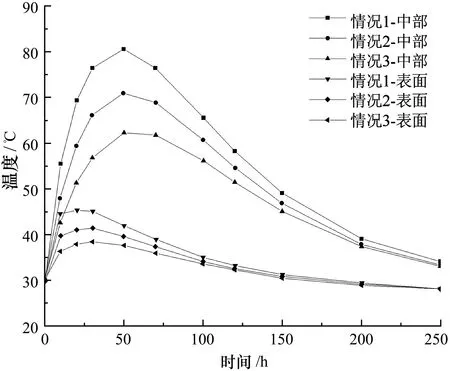
图3 基础中心和表面温度随时间的变化
1.3 第2次分析:分析模型有2种不同混合料的混凝土层
1.3.1 层厚对温度场的影响
第2次分析使用与第1次分析相同的混凝土块(大块基础)。本次分析的基础由2层混凝土构成,其中上层产生的水化热高于下层。上层混凝土的m(水泥∶粉煤灰)=100%∶0%;下层混凝土的m(水泥∶粉煤灰)=80%∶20%。1 m3混凝土块按照不同厚度制备4个试件,如表3所示。

表3 4个试件的厚度 m
图4为4个试件对应的基础中心和表面的温度变化。在浇筑混凝土后50 h,观察到4个试件的峰值温度分别为62.7,63.6,65.4,68.1 ℃;混凝土块中心和表面之间的最大温差分别为24.4,24.0,24.6,26.6 ℃。由图4可知,试件2在浇筑50 h后的混凝土块中心和表面的最大温度差在4个试件中最小,上下层划分为1/4的混凝土产生的热应力最低,在混凝土强度发展初期不宜超过其抗拉强度,形成热裂缝。此时,上层混凝土能产生比下层更高的水化热,表面混凝土向周围环境的热量损失率高于大体积混凝土块的核心部分,这有助于最大限度地减少中心部位和混凝土块表面之间的温差,并降低中心部位的峰值温度。因此,对于2.5 m×2.5 m×2.5 m基础,试件2的上下层厚度最佳。

图4 4个试件的基础中心和表面的温度变化
1.3.2 混凝土配合比对温度场的影响
固定试件的下层厚度为2.0 m,混凝土混合料中m(水泥∶粉煤灰)=80%∶20%;上层厚度为0.5 m,按照表4所示改变上层混凝土混合料中胶凝材料的配比,分别制备3个试件。分析不同混凝土混合物对大体积混凝土块中温度场的影响。

表4 上层混凝土胶凝材料的配比 %
图5为3个试件的基础温度变化。混凝土浇筑后50 h,再次观察到3个试件混凝土块中心的峰值温度分别为63.6,62.9,62.6 ℃。3个峰值温度相差不大,是因为3个试件下层的混凝土混合料都相同。3个试件混凝土块中心部位和表面之间的最大温差分别为24.0,24.2,24.4 ℃,说明试件1的温差最小,这是因为上层没有粉煤灰,与试件2、3相比,产生的水化热最高,有助于减少基础核心和表面之间的温差。

图5 3个试件的基础中心和表面的温度变化
综上可以得出结论,试验块应分为2层,厚度分别为0.5 m和2.0 m。2层混凝土混合料的胶凝材料(水泥和粉煤灰)质量相同,为385 kg/m3,其中上层无粉煤灰(0%),而下层有77 kg/m3的粉煤灰(占总胶凝材料的20%)。
2 实验研究
制备一块尺寸为2.5 m×2.5 m×2.5 m的大体积混凝土块,混凝土块中2层的配合比和厚度如前所述。所用水泥为普通硅酸盐水泥,最大骨料粒径为20 mm。
混凝土由车载混凝土泵浇筑。使用的模板为钢模板。使用尼龙层和50 mm绝缘层覆盖混凝土表面和模板外部,以防止热量辐射到周围环境中(即加热方法)。
温度传感器安装在实验混凝土块的预定位置(如图6所示),以记录温度随时间的分布。
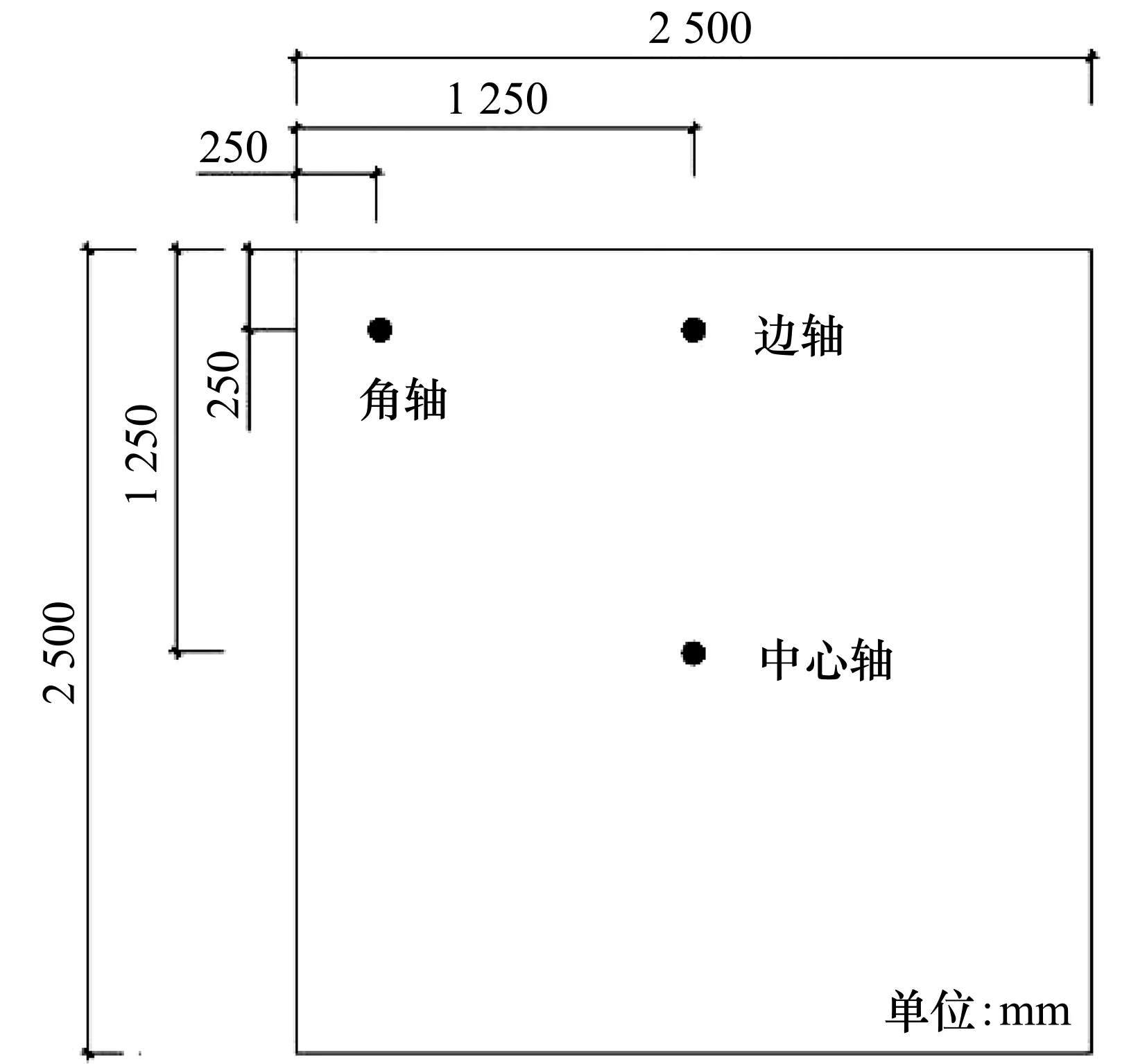
(a)平面上
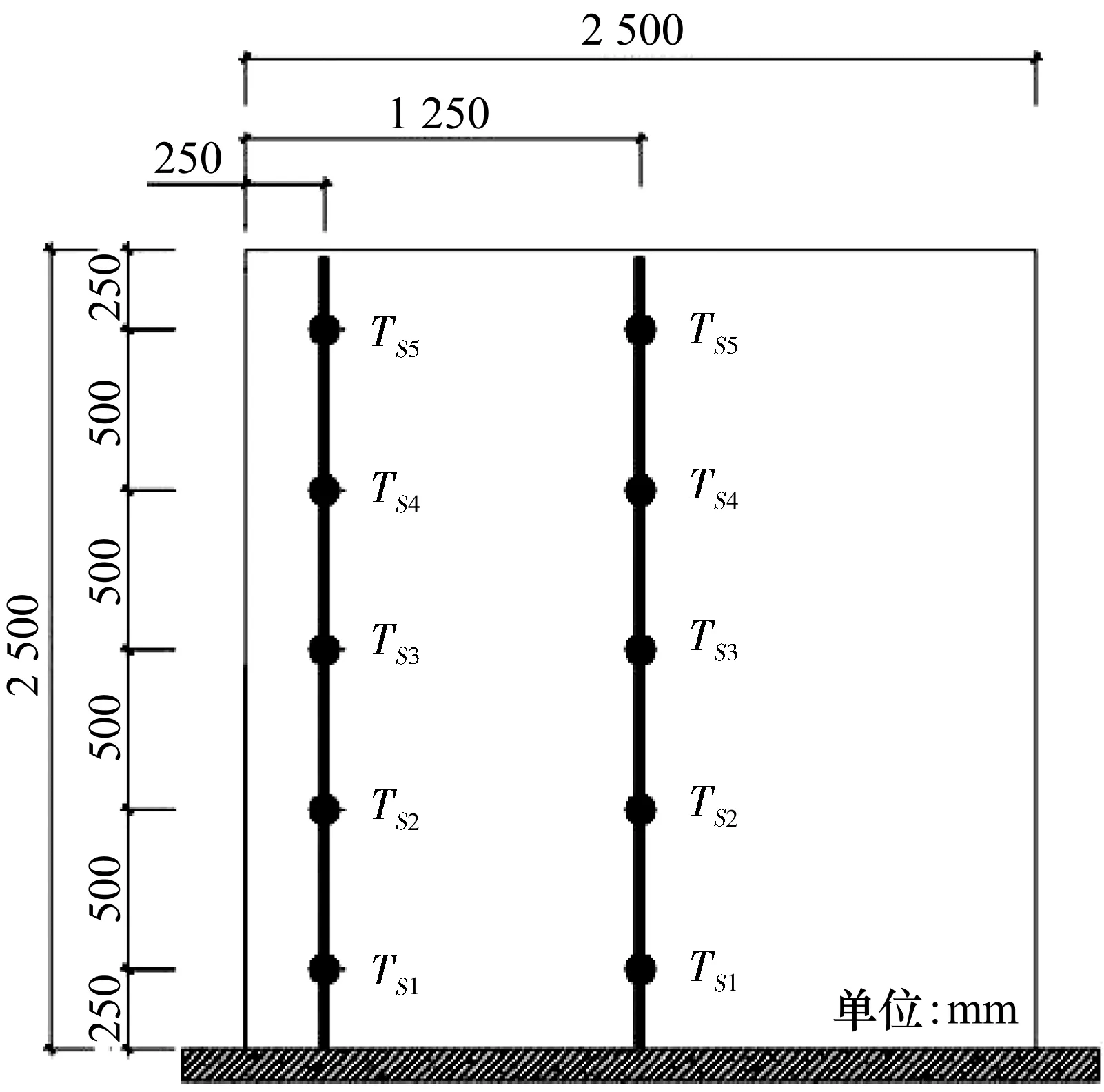
(b)立面上图6 实验区中的热传感器位置
沿块的角轴、边轴和中心轴共有15个测量位置TS(即每个轴5个TS)。在每个测量位置,安装了2个温度传感器,以确保收集数据的可靠性。此外,还收集了周围环境、浇筑混凝土和地基的温度。
3 分析模型验证
在初始建模研究中,使用环境温度、浇筑温度和地基温度的假设值对分析模型进行模拟。为了验证模型,再次使用实验期间收集的实际数据进行模型分析。参数值如表5所示。

表5 建模参数值 ℃
图7为3个测量点的观测温度场和模拟温度的对比结果,即TS3(混凝土块核心处)、TS5和混凝土块表面、混凝土块中心轴上的温度场和模拟温度。可以看出,建模和实验研究在3个测量点提供的温度曲线形状相似,模拟温度值与实验值的偏差很小。混凝土块核心的实验峰值温度TS3为73.7 ℃,模拟值为72.3 ℃。测量点TS5的实验峰值温度为70.2 ℃,模拟值为69.4℃。混凝土块表面的实验峰值温度为60.0 ℃,模拟值为59.2 ℃。实验期间观察到的最大温差为18.3 ℃,模拟值为17.3 ℃。此外,通过对试块内其他测点的实验温度与模拟温度的比较,得出了相同的结论,表明仿真结果可靠。
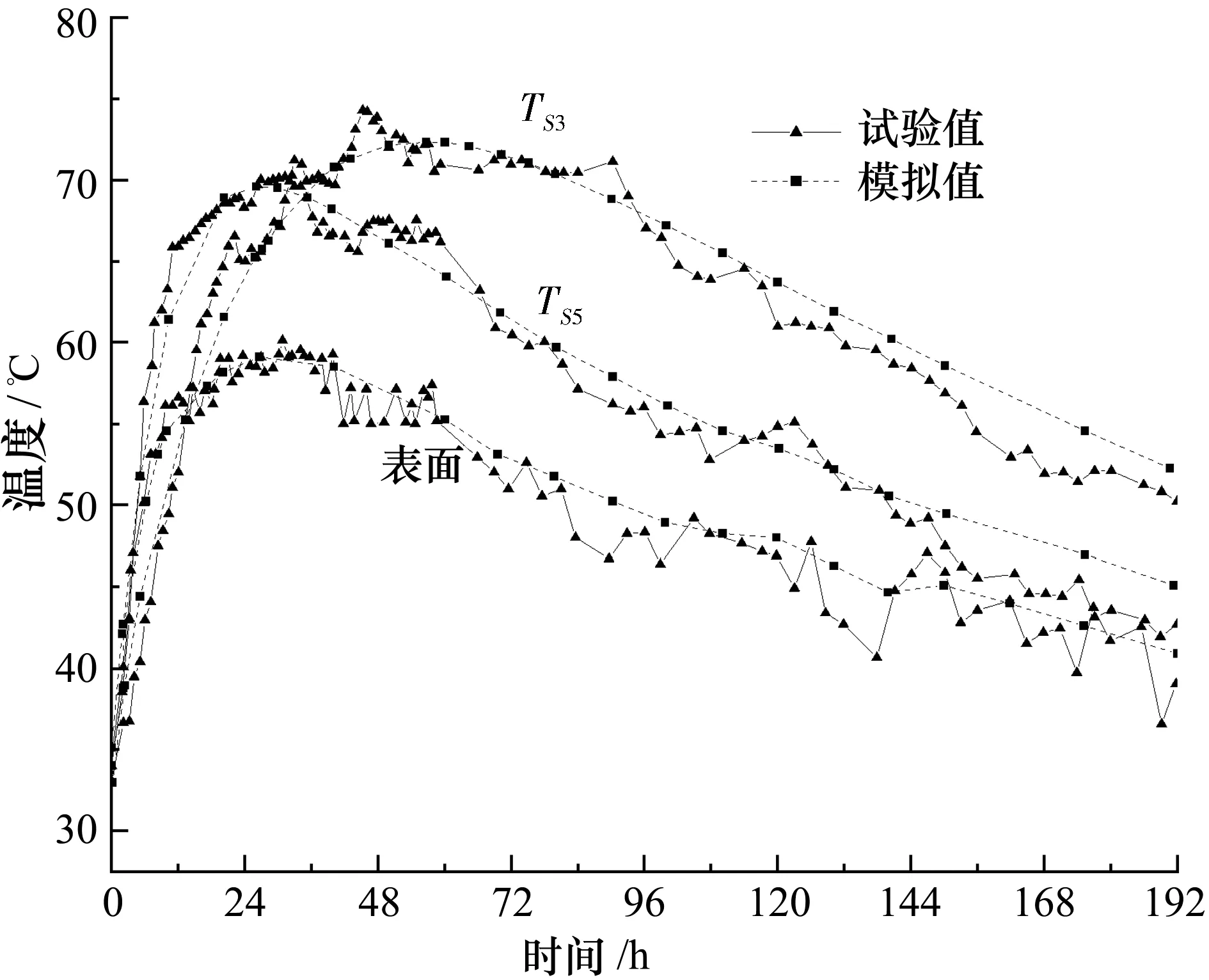
图7 沿试块中心轴测量点处模拟和实验温度数据的比较
此外,混凝土块中部和表面之间的温差观测值和模拟值均低于25 ℃,这意味着混凝土块可能不会因热问题而开裂。这与实验块上没有裂缝的现象是一致的。
4 模型分析与结论
在2.5 m×2.5 m×2.5 m混凝土块上进行的建模和实验研究,证明了使用2层不同混合料的大体积混凝土控制热裂缝的有效性。结果表明,上层会比下层产生更多的水化热,从而减小混凝土块中部和表面之间的温差。表面混凝土的热量损失率高于大体积混凝土块的核心部分。这是导致混凝土块中部和表面温差大的原因,也是导致大体积混凝土产生热裂缝的原因。
分析模型的验证表明,数值模拟提供的分析结果是可靠的。为验证上述研究结论,进一步在5.0 m×5.0 m×5.0 m的基础模型上进行建模研究,分析不同混合料和厚度的影响。包括4种不同上层混合料,其中粉煤灰含量在胶凝材料总量的0%~30%之间变化,以及7种不同上层厚度在0.5~3.5 m之间的情况。其结论与第1节中讨论的结果相似。
此外,对于5.0 m的块体,上部1.0 m的厚度提供了混凝土块核心与表面的最低温差(23 ℃)。研究发现,对于此混凝土块,上层厚度与下层厚度之比为1/4时为最大限度减小温差的最佳划分方案。这个比例也类似于文献[6]中5.7 m块体所用的比例,5.7 m的混凝土块被分为2层,厚度分别为1.2 m和4.7 m,此时对大体积混凝土温度裂缝的控制效果最佳。
