基于遗传算法的智能排课系统的设计

刘 莉,栗 超

(1.烟台职业学院 交通工程系,山东 烟台 264670;2.山东理工大学 计算机科学与技术学院,山东 淄博 255000)

高校课程多、学生多,排课是组合数学理论中所称的非确定性多项式(Non-deterministic Polynomial,NP)问题,具有难解性、复杂性特点[1]。科学合理的课程安排不仅能够提高教师和学生的满意度,同时在提升高校办学质量方面也发挥着极为重要的作用。智能化排课系统不仅能够降低高校教务部门的工作量,还使得排课方案更加科学、合理。宗薇[2]构建了多约束条件下的排课数学模型,采用遗传算法对可行排课方案进行优化,获得最佳的排课方案,使得排课的成功率大大提升,避免了课程之间出现冲突。刘明[3]以“实验室智能管理平台”为基础,采用遗传算法开展智能实验排课,智能优化算法在排课中的应用使得有限资源得到了科学合理利用,提高了教学资源的利用率以及师生的满意度。王运成等[4]指出排课问题可以转化为多约束、多目标优化问题,并采用二叉树知识推理设计了可拓展智能排课系统,有效解决了动态大规模排课需求。尽管各种智能算法在排课中得到了广泛应用,但是实际排课方案还存在较大优化空间。遗传算法作为一种模拟生物进化过程的优化算法,在许多优化问题中具有突出的表现,但是存在受参数设置影响大、易陷入局部最优解的问题。本文构建智能排课的求解优化模型,同时对传统遗传算法进行改进,应用于所构建的优化模型中,得到智能化的排课结果。

1 问题分析

1.1 排课原则

不同专业学生既有相同的课程,也有大量不同的课程,排课是一个多对多的问题。只有坚持排课的基本原则,才能使学生和任课教师满意,同时也能够达到良好的优化效果,使有限的教育资源得到科学、合理地分配。课程排课应该坚持4个基本原则,即没有时间冲突、满足课程最佳上课时间、课程尽量均衡、保持合理间隔[5]。

没有时间冲突是基本要求,同时也是硬性要求,即不能给同一个任课教师在同一个时间安排2门课程,也不能给同一名学生在同一个时间安排2门课程。不同性质的课程有其最佳的上课时间,如英语课安排在上午1～2节相对比较合理,这样能够提高学生学习的积极性和主动性,教务部门在排课时应该给予考虑;数学课难度较大,对学生的脑力消耗较多,不宜让学生连续上,应该保持合理的时间间隔。另外,为确保教师具有良好的讲课状态,排课尽量避免教师连续上4节课。这将直接影响教师的上课质量,进而影响课程的教学效果。在进行排课的过程中应该尽量做到难易结合,确保教师和学生的休息时间,不能过于集中。

1.2 排课约束条件

智能排课问题属于优化调度问题,即学生、教师、课程等在满足排课约束条件下被安排在特定的时间、特定的场所上课,使得资源得到充分利用,上课效果最佳。按照课程排课的原则,构造排课约束条件:

1)学生上课时间不发生冲突,即:

(1)

式中:L为课程类别数;H为课程教师人数;P为场地数;cn为学生;dm为时间;kl为课程;th为教师;rp为教学场所。

2)教师上课时间不发生冲突,即:

(2)

式中,N为班级所能容纳的学生最大值。

3)上课场所不发生冲突,即:

(3)

式中,H为教师人数的最大值。

排课不冲突,即学生上课时间不冲突、教师上课时间不冲突、上课场所不冲突,这是智能排课的硬约束,满足硬约束的排课方案是可行方案,但未必是最优排课方案[6]。为了使智能排课方案最优,课程的上课时间要尽量满足学生和教师的要求,均匀分布,同时要对上课的场所充分利用,避免有的场所使用过于频繁,而有的场所长期被闲置。

2 模型构建

2.1 课程编码

不同的课程编码方式导致智能排课的效率存在较大的差别。传统遗传算法采用二进制编码方式,效率较低[7]。本文采用十进制对课程进行编码,如图1所示。

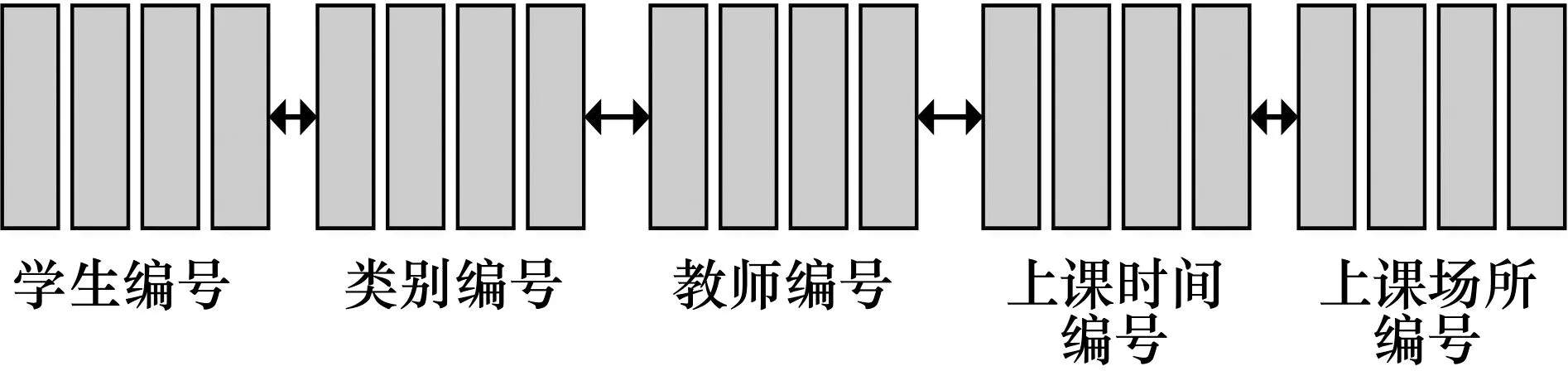
图1 课程编码示意图

例如:编码1120-1021-0403-1125-1024,其中1120为学生编号;0403为教师编号;1021为课程的类别编号;1125为上课时间;1024为上课的教室编号。

2.2 适应度函数

(4)

式中:gi(i=1,2)为上课时间;mi(i=1,2)为上课时间段;μ1和μ2为对应的权重系数;δfit为理想评价值。课程安排合理度o定义为:

(5)

智能排课模式适应度函数f定义为:

(6)

式中:n为学生总数;oi为第i个学生课程安排合理度。

2.3 选择操作

选择操作是遗传算法中体现“适者生存”的关键一步,传统遗传算法采用轮盘赌法进行选择操作,即将个体轮盘划分为不同比例的区域,区域的大小由个体的适应度来确定[8]。个体适应度值越大,在轮盘中所占的比例越高,生存的概率越大,进入下一代群体的概率也越大,具体如图2所示。

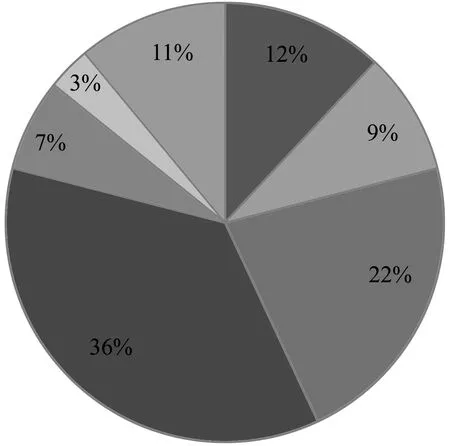
图2 轮盘赌法选择示意

由于轮盘赌法只考虑旧种群个体,导致种群个体的多样性减少。为增加种群个体的多样性,采用蒙特卡洛概率接受法进行选择操作。蒙特卡洛采样过程为[9]:

假设马尔科夫链的状态转移概率ρ和当前种群中的最优个体x0、新生个体x1有关,平稳分布π(x)状态转移次数阈值为n1,在每一次迭代过程中进行n1状态转移。从矩形分布U(0,1)中随机采样获得u,如果u<ρ,那么接受最优个体x0、新生个体x1;如果u≥ρ,那么不接受状态转移。

选择操作方法为交叉变异产生新个体优,则接受产生的新个体;交叉变异产生的个体劣,以概率σ接受新个体,即蒙特卡洛概率接受法,概率σ称为接受概率,其数学表达式为:

(7)

式中:Ei(i=1,2)为个体适应度,1为旧个体,2为新个体;KT为常量。

2.4 交叉变异

交叉与变异操作直接影响遗传算法的性能,通过个体的交叉组合来获得优异个体,同时通过个体的变异操作来获得新的优异个体。遗传算法染色体交叉操作确保种群的多样性,避免遗传单一化,一般选择交叉概率大于0.9。遗传算法变异操作是自然界在物种选择过程中出现的突发情况,变异使得种群的多样性扩大,一般选择变异概率小于0.1。

由于传统遗传算法交叉与变异概率是固定值,导致在进化的后期个体变得比较单一,缺乏多样性,进而算法陷入局部最优的状态。为避免这种情况的出现,采用自适应交叉与变异操作,即:

(8)

(9)

式中:Pc为交叉概率;Pm为变异概率;k1和k2为区间(0,1)上的随机数;fl为交叉个体适应度值;favg为交叉个体适应度平均值;f1为变异个体适应度值;Navg为变异个体适应度平均值。

2.5 智能排课系统

基于遗传算法的智能排课系统首先对排课问题初始化,产生遗传算法的初始化种群,采用十进制对课程进行编码,计算每一种排课方案的适应度值,并判断当前排课方案是否为最优排课方案。如果是最优排课方案,那么直接输出;如果不是最优排课方案,继续迭代。计算新一代种群的个体适应度值,直到该方案为最优排课方案,输出结果即为智能排课的结果。基于遗传算法的智能排课系统流程如图3所示。

3 仿真分析

3.1 数据来源

以浙江省某职业院校为例,大二年级学生数量为3 620人,教师人数为42人,涉及的教学任务共96个,其中专业基础课共12门,专业选修课为20门,提供课程教学的场所共28个。

3.2 仿真结果分析

为了对比改进遗传算法和传统遗传算法在智能排课方面的性能,分别采用传统遗传算法和改进遗传算法进行排课分析,参数设置见表1。

图3 智能排课系统流程

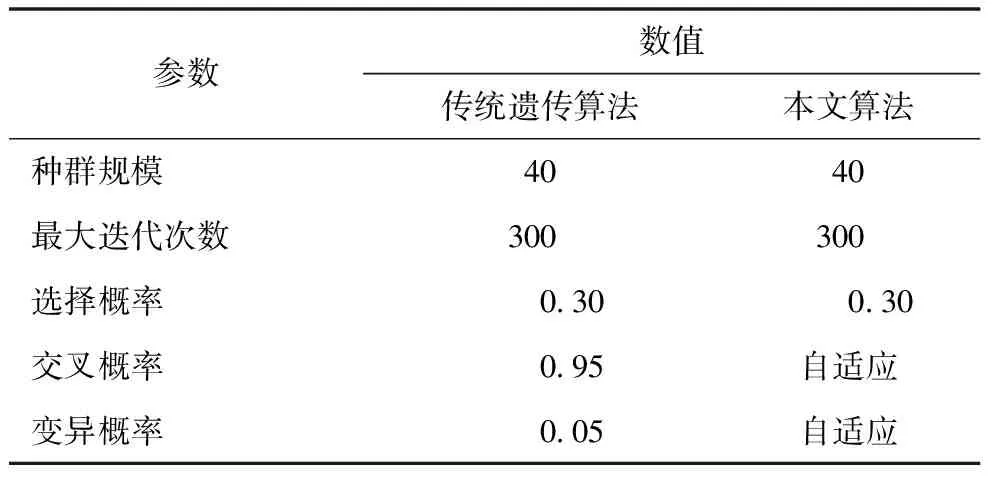
表1 算法参数

为了消除参数选择过程中各种随机因素的影响,采用传统遗传算法和改进遗传算法进行6次仿真试验,取6次仿真结果的平均值进行对比,其迭代次数和平均适应度值关系如图4所示。

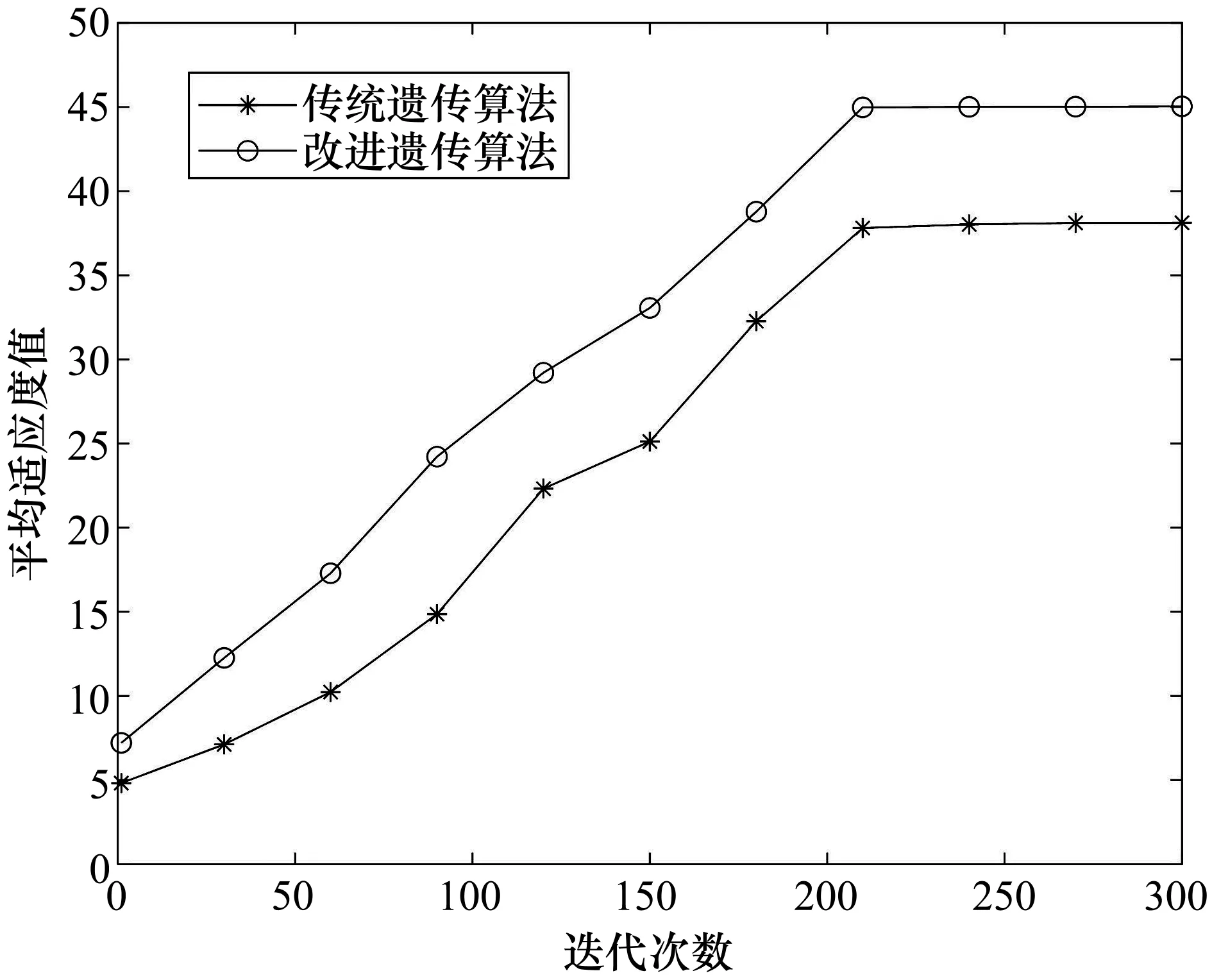
图4 迭代次数和平均适应度值关系

由图4可知,对遗传算法进行改进后获得最优排课方案所需要的迭代次数减少。将传统遗传算法得到的排课方案和改进遗传算法得到的排课方案进行对比,结果表明改进遗传算法得到的排课方案对教学资源的利用率更高。

4 结论

本文对传统遗传算法的选择操作采用蒙特卡洛概率接受法改进,交叉和变异操作采用自适应概率改进,提出且构建了基于改进遗传算法的智能排课模型,应用于浙江省某职业院校,与传统遗传算法排课模型进行对比。结果表明,基于改进遗传算法的智能排课模型在解决排课问题上更具优势,提高资源利用率。这对促进高校教学质量的提升具有一定的实际意义。