基于Kinect的3D全景图像扫描重建技术

黄君君

(福建农业职业技术学院 信息工程学院,福州 350007)

计算机视觉是指通过摄像头、传感器和计算机等设备代替人眼对物体进行识别、跟踪和分析[1]。目前,获取视觉三维模型的方式有3种:1)根据物体的几何外观直接生成,通常是利用三维处理软件建模,其特点是制作1个模型所需要的时间长,对操作人员的技术要求高,同时细节处也可能无法顾及[2];2)借助三维扫描仪器设备对物体建模,但局限于单个对象建模[3];3)通过计算机视觉重建目标物体的三维模型,这种方式不受物体形状限制,建立的模型逼真,现实感强,而且设备价格便宜[4]。但第3种方法的主要问题是:1)如何采集获取物体的三维信息,并对这些信息中存在的各种噪音进行滤波[5];2)如何保证三维重建的精度以及加快三维重建的速度[6]。传统的迭代最近点(Iterative Closest Point,ICP)算法存在耗时长的问题[7]。本文针对传统ICP算法存在的问题提出基于K维树(K-Dimensional tree, K-D tree)以及筛选策略的改进ICP算法,并进行三维重建实验,验证当前算法的有效性。

1 三维模型设计与实现

1.1 总体设计方案

本文基于微软推出的体感设备Kinect进行三维点云重建,重建的流程如图1所示。

1)Kinect获取深度图像

三维重建的重要步骤是采集深度信息和RGB图像,通过Kinect采集深度信息和RGB图像。采用Kinect采集深度信息前,需要对Kinect相机进行标定,标定的过程为:通常情况下Kinect采集深度图像的范围为镜头前1～5 m,将这4 m的距离均匀分成40份,每份的间隔为10 cm,选择1个参考平面测试,依次采集参考平面在这40个位置上的散斑图像[8]。使用Kinect采集深度信息时,将获取的实时散斑图像与前面已经标定好的40份散斑图像进行相关的运算,得到40份差异的散斑图像。由差异散斑图像的具体像素值可以计算出深度信息,计算方法如图2所示。

图1 三维点云重建流程

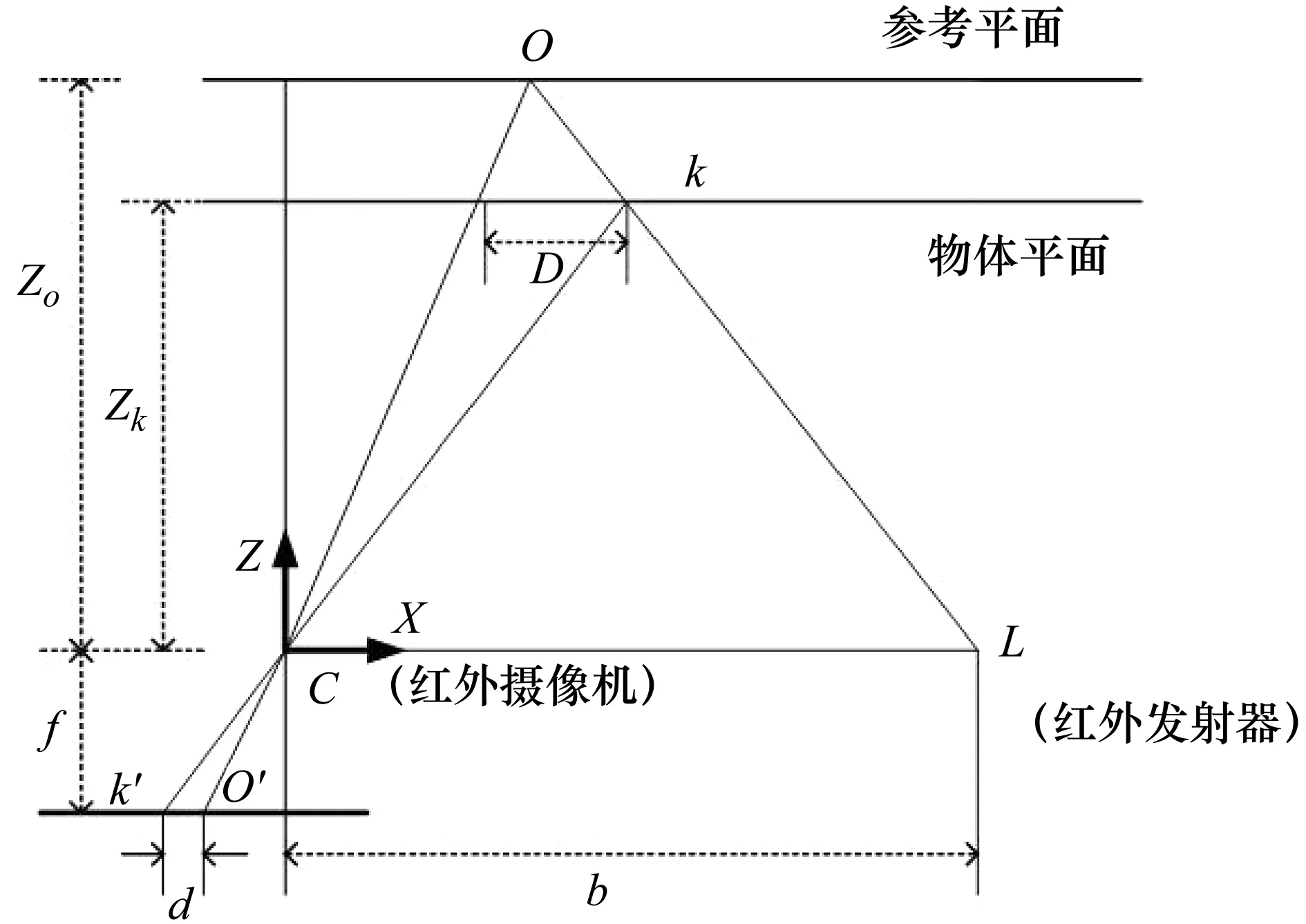
图2 深度信息计算原理

从图2可知,由红外发射器反射红外线,红外线照射到参考平面上时,形成镭射散斑O,红外摄像机采集到散斑点O后,内部成像为O′点。面对实际测量的目标物时,红外发射器发射红外线在物体表面形成镭射散斑点,经红外摄像机采集在内部成像k′点[9]。由上述表达已知:参考平面到此时Kinect的距离为Zo,Kinect红外摄像机的焦距为f,红外摄像机与红外发射器之间的距离为b,物体的散斑点与参考平面散斑点的距离为d,由这几个参数便可计算出物体平面到Kinect的距离。

2)获取深度信息和RGB图像

由于Kinect相机1次只能获取1个角度的深度信息和RGB图像,同时拍摄图像还会受到物体形状和拍摄范围的限制,不能一次性获取物体或者建筑环境的全部信息。因此,需要操作人员移动Kinect相机对场景进行连续多方位拍摄。

3)滤波及预处理

对深度图像采用双边滤波算法。双边滤波是在高斯滤波算法的基础上开发的,在起到良好降噪作用的同时,还能够不丢失深度图像的边缘信息,其具体算法为[8]:

(1)

式中:kd(x)为归一化系数;c(ξ,x)是中心点与该中心点所在的领域内点空间相似度的函数;f(ξ)为滤波前所对应点的灰度值大小的函数。该滤波算法将点x附近邻域与它邻近的点赋予了不同的权重,所以能够使滤波后的图像更加平滑,减少黑洞的同时保护边缘信息,使背景信息更加明显。

4)图像特征提取

Kinect设备采集到目标物的三维点云数据后,需要将RGB彩色图像转化为灰度图像,然后进行提取图像中的特征点。提取图像特征时采用加速鲁棒性特征(Speeded Up Robust Features, SURF)提取算法[9]。

5)点云配准的初始匹配

提取完特征点后,将相邻的2帧图像的特征点进行初始匹配。用1个向量来表示特征点,这个向量也称作特征描述子[10]。现在有2帧图像I1和I2,它们的特征描述子的集合分别为X={x1,x2,…,xn}和Y={y1,y2,…,yn},计算它们之间的欧式距离[10]:

(2)

将欧式距离D(x,y)作为衡量两者相似性的度量,D(x,y)越小,表示特征点的相似程度越高。特征点匹配的方法是:根据式(2)寻找最相似的匹配点,将图像I2中的所有特征描述子依次和图像I1的特征描述子向量进行计算比较,求得的D(x,y)最小的1对特征描述子便是最佳匹配的特征点,按上述过程重复I1中所有的特征描述子,求得所有的最佳匹配的特征点。

1.2 点云拼接算法的拼接分析

ICP算法是基于最小二乘法原理的最优匹配算法。ICP算法求解变换参数是关键,对旋转和平移用以下7个参数向量表示[7]:

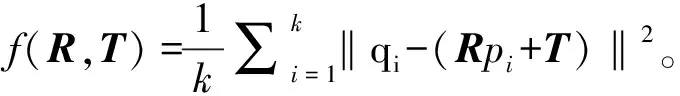
(3)

式中:R=[q0qxqyqz]表示旋转矩阵;T=[txtytz]表示平移矩阵。

ICP处理过程如下:找出曲面S上对应目标点集Pk中点的点坐标的最近点的集合Prk。针对点集Pk和Prk,先计算出它们的重心的坐标,再将点集中心化,获得新的点集和它的正定矩阵N。计算出最大特征向量,也就是残差平方和最小的旋转矩阵R。计算出R和T确定变换参数后,再借助2个坐标的重心进一步求出2个点集的重心的差值。由R、T向量迭代后生成1个新的点集Pk+1。迭代终止的条件为目标距离的平方和小于设定的阈值即迭代结束。ICP迭代结束后就完成点云数据的拼接,得到完整的三维模型。单次迭代点云拼接的伪代码如下:

Input:

q∈Q;参考点

p∈P;待匹配点

R0;初始3D旋转矩阵

T0;初始3D平移矩阵

Output:

R;最终3D旋转矩阵

T;最终3D平移矩阵

1Ptem=Reproject(P,R0,T0);位姿变换过程

2 for iter is 1 to max_iter do

3 [Ptem]=Search NN(Q);搜索最近点过程

4 [Rt]=Estimate Trans (Ptem,Q,Rtem,Ttem);求解最终姿态变换矩阵

5 P′-Reproject(Ptem,Rt);

6 end for

7 returnRt;

1.3 改进ICP算法的拼接分析

传统ICP算法只对三维模型的表面结构感兴趣,也就是只采用深度信息,没有关注3D点云的RGB图像信息。同时存在着查找最近点的速度慢和效率低的问题,并且传统ICP算法鲁棒性较差,匹配点对时容易出现大量错误点对。本文提出了基于K-D树的改进ICP算法。K-D树分为三维,在每一维上都依据坐标的大小分开所有子节点。首先第一维坐标小于根节点安排在左子树,大于根节点就安排在右子树。同理第二维和第三维也按相同的方法安排。三维K-D树结构如图3所示。

图3 三维K-D树结构

K-D树搜寻方式是循环搜寻,需要执行回路追踪,追踪到根部以找到最近点。要增强系统的鲁棒性,则需要剔除系统的异常值。目前有很多种方法剔除异常值,如阈值法是将点对的距离与设定的阈值相比较,若大于阈值,则剔除该异常点对,即将它的权重赋为0。或者将距离换成均方差等。采用线性最小二乘方法优化点到切平面目标函数,并提出一种新的匹配点对筛选策略。采用K-D树搜索点云域中原始点云P的k个最临近点的集合Pk,其搜索领域半径为[11]:

(7)

式中,Pk={Λ(1),Λ(2),…,Λ(k)}。

改进ICP算法流程如下:点云初始配准。使用奇异值分解法达到点对点距离函数的最小化,即计算原始点云P和目标点云Q去中心化的协方差矩阵;从而计算得到初始配准的矩阵;然后对原始点云数据中所有的点P采用初始配准矩阵进行旋转平移变换。不断循环迭代下面的过程,直至满足迭代的次数大于最大迭代次数或者相邻的2次配准的矩阵的差值小于设定的阈值。存在原始点云数据集合中的点P,采用K-D树搜寻的方式在目标点云Q中寻找最近的点y,作为待处理的匹配点。筛选匹配点对,并保留符合约束条件的匹配点对集合,采用线性最小化二乘法使目标函数最小化,可计算出匹配点对和之间的最优变换T;通过变换矩阵T经旋转和平移更新上一次迭代的原始点云P。

2 实验及结果分析

2.1 实验设备环境及操作方法

实验在普通封闭的室内环境下进行,同时注意避免强光源等的干扰。实验设备为Linux系统的计算机和Kinect设备,硬件要求低。开发工具和软件平台是:C++、OpenCV和CodeBlock。操作过程为:启动Kinect和相关软件后,操作人员手持Kinect设备从固定点开始采集深度信息和RGB图像,Kinect设备应该保持离墙壁或者目标物2 m的距离,观测电脑上的实时特征点采集情况,缓慢移动Kinect设备,扫描全室内的环境和物品,同时使Kinect设备在室内移动1个完整的闭环,但也要注意避免出现突然跳跃扫描1个与当前特征点不相邻的物体。当Kinect设备回到最初的起点时,扫描完成。退出当前软件,执行数据处理配准和融合重建后便可生成三维模型。

2.2 传统ICP和改进ICP重建效果对比

1)单一场景模型

传统ICP算法所建立的三维模型如图4(a)所示。采用改进ICP算法测试结果如图4(b)所示。

(b)改进ICP算法模型

图4(a)中所标的1和2处的椅子腿有明显的重影,也就是产生了错乱的情况。错乱产生的原因可能是异常值没有及时剔除或者是干扰等问题造成的累计误差过大,所以需要降低三维重建过程中产生的误差。图4(b)中的椅子轮廓清晰,外表无重影,没有出现图4(a)中椅子错乱重叠的情况,三维重建的模型效果大大优于传统标准的ICP算法,图4(b)能够直接地反映椅子的颜色、外观、规格等参数,说明改进ICP算法的三维重建效果有较大进步。

2)多场景模型

为了验证改进ICP算法在多场景模型中的重建效果,分别进行平层公寓和复式公寓的测试,结果见图5。图5(a)是1幅平层公寓室内环境的三维重建图,包含1个小隔间,该模型清晰反映了室内的物体摆放情况和建筑轮廓,同时室内物品没有发生错乱,说明改进ICP算法在多场景下的三维重建效果佳,克服了传统ICP算法重建速度慢以及部分区域容易发生错乱的情况。图5(b)是1个复式公寓的一楼的三维模型,该模型清晰反映了该公寓的建筑结构、装修风格和物体的布置情况,也说明基于Kinect的室内重建不仅仅可以应用于单一封闭房间,还能用于多个连通房间的相对封闭环境完成三维重建,并且效果良好,未来可以广泛应用于建筑、售房、考古等行业,通过三维重建的模型可以在电脑上直观详细地了解房间建筑的具体情况。

(a)平层公寓三维重建模型

(b)复式公寓三维重建模型

2.3 传统ICP和改进ICP耗时对比

改进ICP算法相较于传统ICP算法在处理速度上也大大改善。对单一场景模型和多场景模型分别进行耗时测试,如表1所示。

在单一场景模型中,通常完成1个面积在30 m2的房间三维重建,传统ICP算法的处理时间为1.31 min,而改进ICP算法计算的处理时间为0.67 min;在多场景模型中,通常完成1个面积在30 m2的房间三维重建,传统ICP算法的处理时间为8.06 min,而改进ICP算法计算的处理时间为5.23 min,速度大大加快,同时也能节省计算机的内存。此外,在重建模型的点云匹配残差均方根误差(Root Mean Square, RMS)方面[12],改进ICP比传统ICP的RMS值更低,说明改进ICP算法的重建精确度更高。

表1 不同模型重建耗时比较

3 结语

针对传统三维重建耗时长和设备昂贵的问题,本文提出了基于Kinect的3D全景图像扫描控制系统,该系统不必使用大型专业激光扫描设备,仅仅依赖Kinect和计算机便可完成普通的室内三维重建,对环境的适应性强,简单易操作。对三维重建的过程进行了实验验证,比较了2种ICP算法拼接的三维模型图,分析了误差产生的原因。结果表明,改进ICP算法能够很好地完成室内三维模型,三维重建速度较快,误差小,没有明显的物品位置错乱等情况,整体轮廓清晰,能满足日常需要。