数形结合思想在解立体几何题中绽放——兼谈2022年全国高考立体几何解答题

洪昌强

(浙江省台州市第一中学,浙江 台州 318000)

纵观2022年全国各地高考立体几何解答题,常以三棱锥、三棱柱等几何体为背景, 如北京高考卷第17 题、 全国新高考Ⅰ卷第19题、2022年浙江高考卷第19题、全国高考乙卷理科第18题等.在处理这些空间问题时,通过建立形与数的联系,探索解决问题的思路.高考以此考查学生运用数形结合思想的能力,检测学生的直观想象素养.下面以2022年全国各地高考立体几何解答题部分试题为例,对解题思路进行剖析.

1 由形定性,以性助数

例1(2022年北京高考卷第17题)如图1,三棱柱ABC-A1B1C1中,侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,AB=BC=2,M,N分别是A1B1,AC的中点.

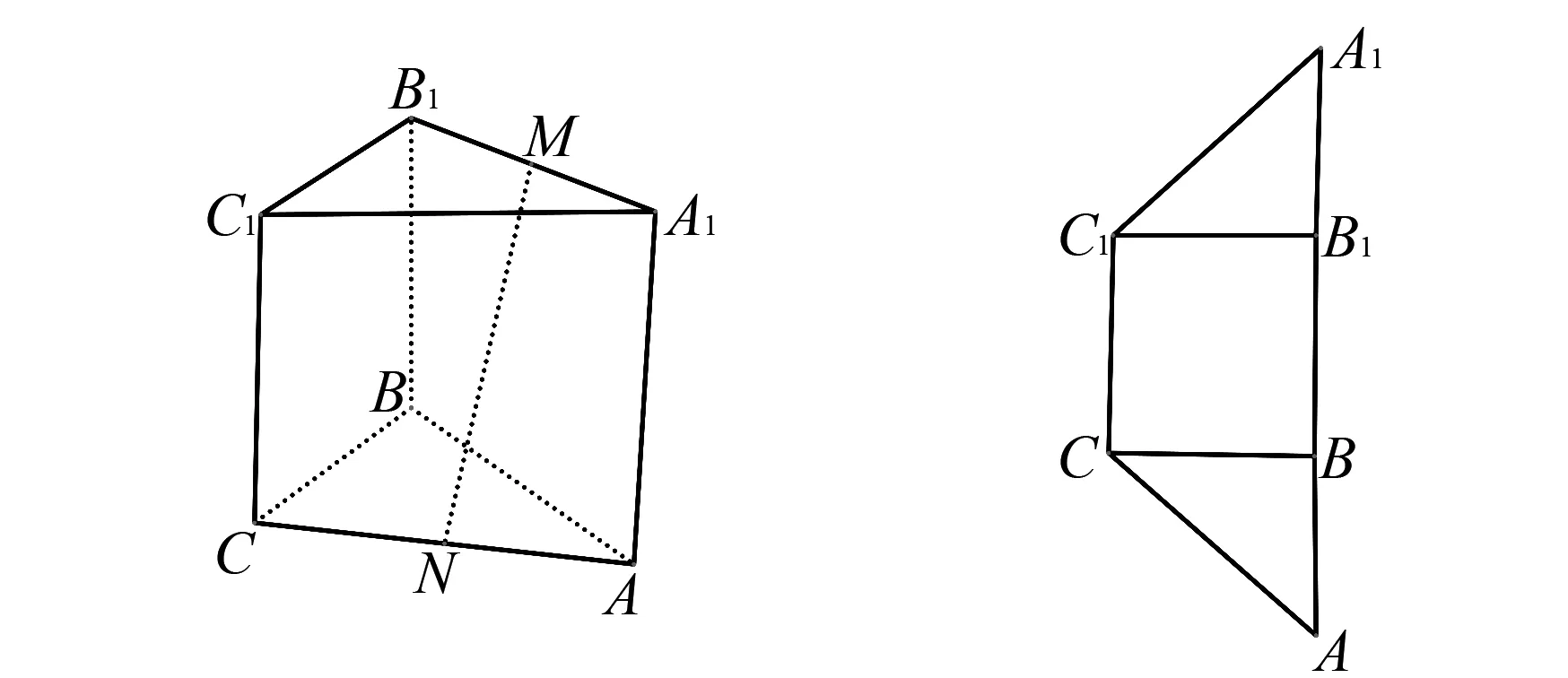
图1 2022年北京高考卷第17题图 图2 例1解析图(a)

(1)求证:MN∥平面BCC1B1;

(2)从以下两个条件①AB⊥MN;②BM=MN中选一个作为已知,求直线AB与平面BMN所成角的正弦值.

分析考查三棱柱ABC-A1B1C1的结构特征:从侧面BCC1B1为正方形得CB⊥BB1且CB=BB1,得知这个三棱柱的底面是等腰三角形,一个侧面是正方形.条件“平面BCC1B1⊥平面ABB1A1”有何作用?此时自然想到平面与平面垂直的性质.并由此得∠CBA=90°.又因为AB=BC=2,所以底面CBA是等腰直角三角形.表明三棱柱ABC-A1B1C1虽然还没有确定,但可以将三棱柱ABC-A1B1C1视为由等腰Rt△CBA和等腰Rt△C1B1A1分别沿BC和B1C1翻折而成,如图2,并且三棱柱随二面角C1-CB-A的平面角∠B1BA大小而变动.

对于第(1)问,虽然三棱柱还没确定,但几何体的一些特征可以确定, 取AB中点为O,因为N为AC中点,M为A1B1中点,则MO∥BB1,NO∥BC.因此,平面MNO∥平面BCC1B1,即得MN∥平面BCC1B1.

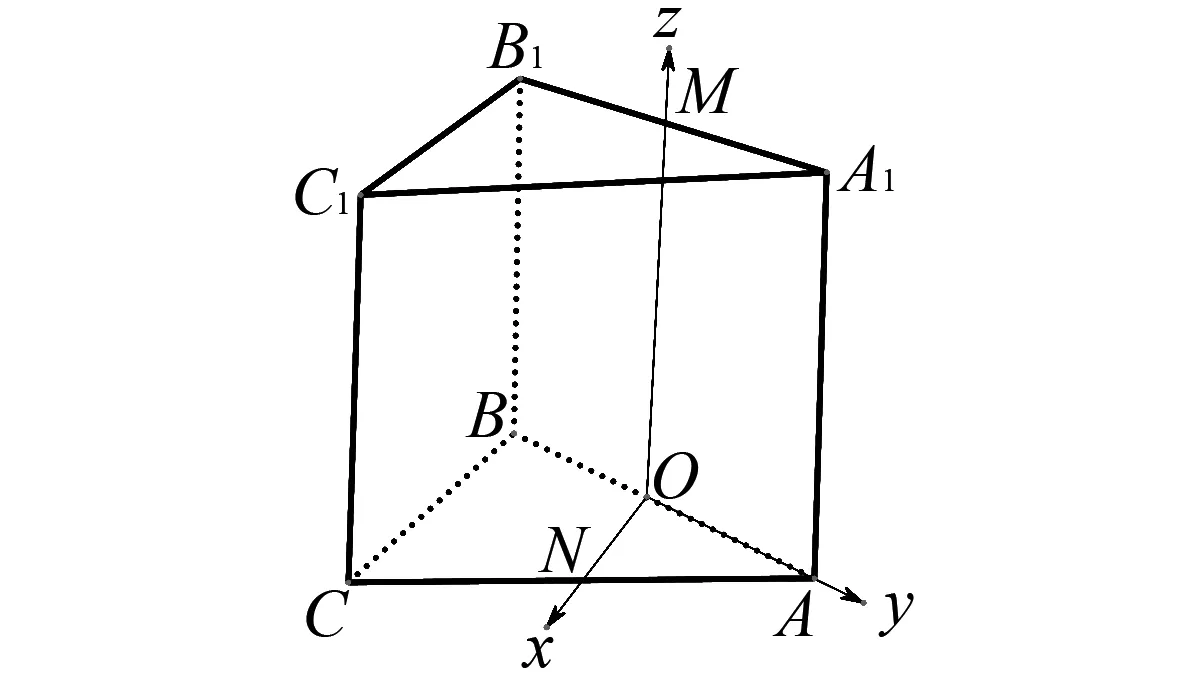
图3 例1解析图(b)

评注一个几何体的特征,常常在点、线、面之间位置关系中体现,而点、线、面之间位置关系必定存在相对应的数量关系.本题的关键是由条件“侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1”和平面与平面垂直的性质定理推断出“∠CBA=90°”.由条件“AB⊥MN(或BM=MN)”推断出“∠ABB1=90°”.由形得数的过程,就是从观察几何图形中点、线、面的位置关系着手,寻找几何特性,从中挖掘有价值的数量关系,然后将各个信息联合在一起,通过逻辑推理,推断出有价值的结论.

2 以数养性,以性定形

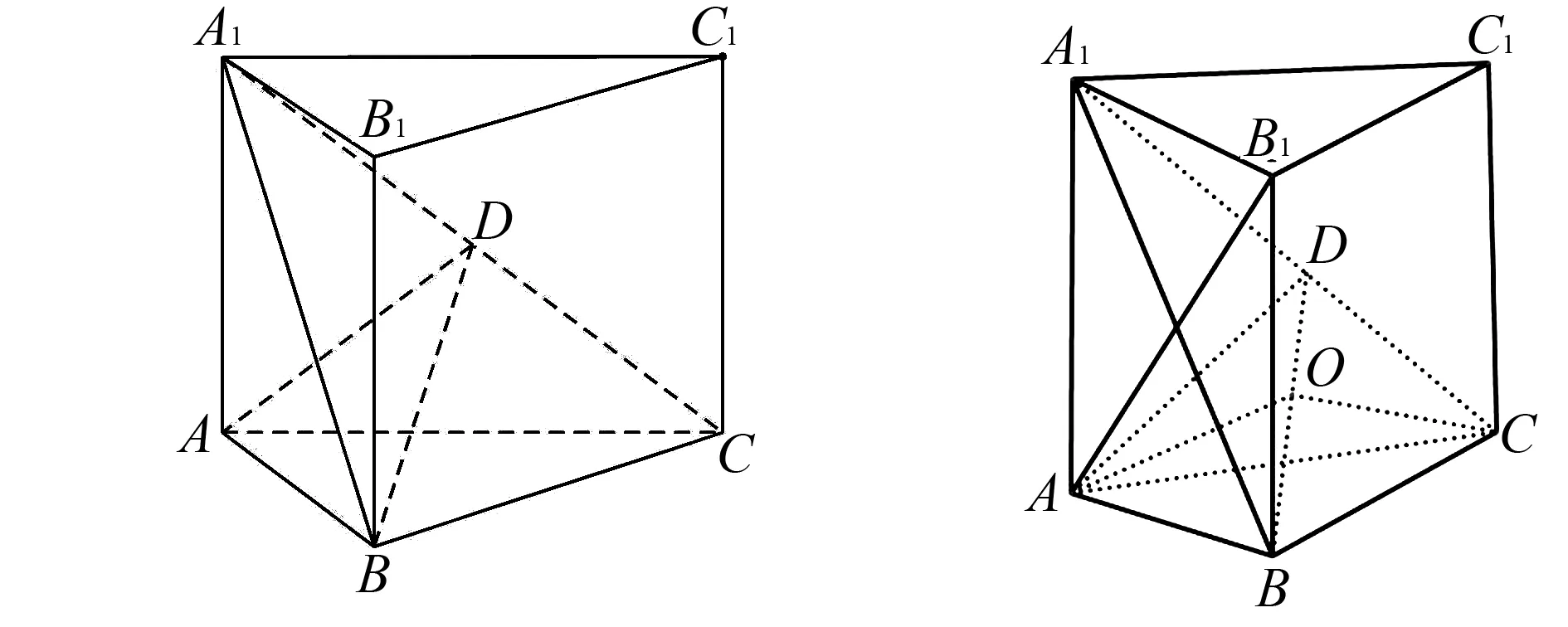
图4 2022年全国新高考Ⅰ卷第19题图 图5 例2解析图

(1)求A到平面A1BC的距离;

(2)设D为A1C的中点,AA1=AB,平面A1BC⊥ 平面ABB1A1,求二面角A-BD-C的正弦值．

3 数形互化,以性制胜

例3(2022年浙江高考数学第19题)如图6,已知梯形ABCD和CDEF都是直角梯形,AB∥DC,DC∥EF,AB=5,DC=3,EF=1,∠BAD=∠CDE=60°,二面角F-DC-B的平面角为60°．设M,N分别为AE,BC的中点．

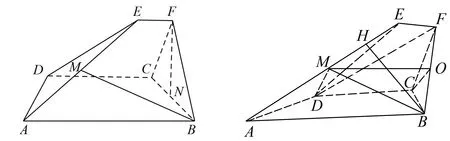
图6 2022年浙江高考数学第19题图 图7 例3解析图

(1)证明:FN⊥AD;

(2)求直线BM与平面ADE所成角的正弦值.

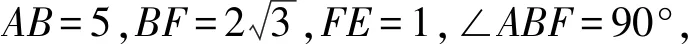
评注利用几何综合法求直线与平面所成角大小,关键是寻找直线在平面上的射影.在研究比较复杂的几何体时,几何体的一些重要几何特征常被遮掩,导致解题思路受阻.本题条件给出的几何体是一个五面体,点B在平面ADE上的投影点位置较难发现.根据条件所提供的数量关系,通过数形结合思想,感知BM与平面ADE有特殊位置关系,由此获得有价值的重要解题信息,被隐藏的直线与平面所成角才显露出来.试题给学生提供了较大的思考空间,对知识之间的联系、直观想象等素养做了深入的考查,突出了对发散性思维和创新性思维的考查.

例4(2022年全国高考数学乙卷理科第18题)如图8,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC中点．

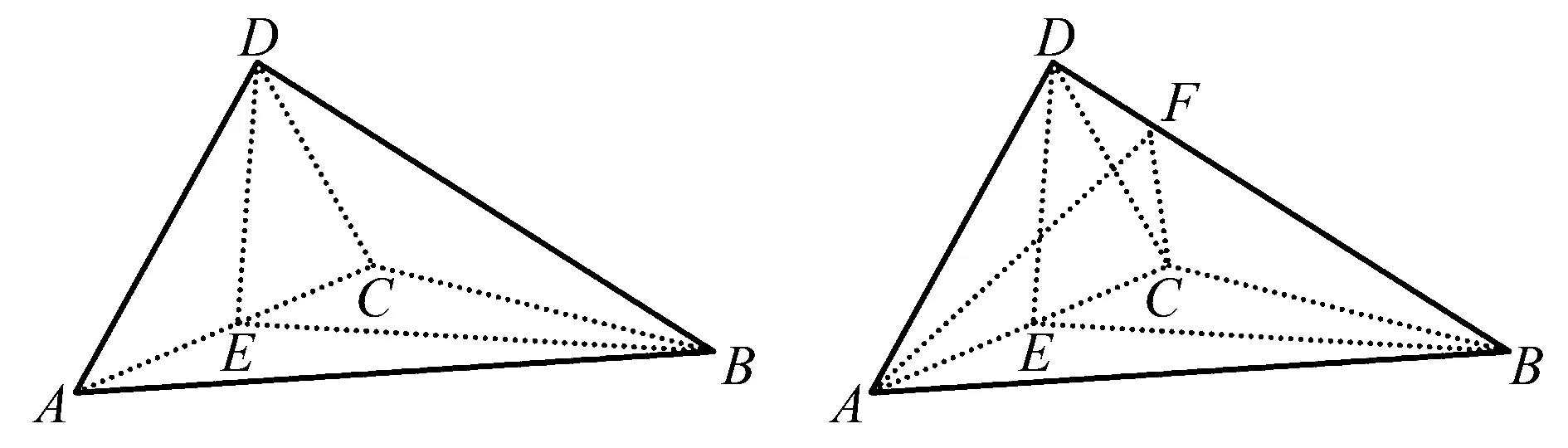
图8 2022年全国高考数学乙卷理科第18题图 图9 例4解析图

(1) 证明:平面BED⊥ 平面ACD;

(2) 设AB=BD=2,∠ACB=60°,点F在BD上,当 △AFC的面积最小时,求CF与平面ABD所成角的正弦值．

分析对于第(1)问, 以形定性,由AD=CD,∠ADB=∠BDC,得△ADB≌△CDB,四面体具有对称性.又因为E为AC中点,AB=CB,所以,BE⊥AC,DE⊥AC,即AC⊥平面BDE,故平面BED⊥ 平面ACD.

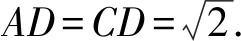
评注本题的几何体特征没有直接给出,而是从条件所提供的有关各个数量关系中,发现几何体中相关的点、线、面所处的位置有良好的特性,受这些特性的启发,激活了解题思路.在研究空间几何体各种距离和角时,如何找到平面垂线的合适位置,是解决问题的关键,而平面与平面垂直的性质定理在找平面的垂线中可以发挥重要作用.在处理立体几何一些问题中,以数定性、由性求数、数形互化,是解题常用的重要思想方法.

如何灵活运用数形结合思想,提高空间想象能力?首先,需要扎实的几何基本知识.合理、有效的想象需要一定知识和经验积累支撑,几何概念、公理、定理和性质是想象的根基,也是直观想象合法保障.具有扎实的几何基本知识,才能使几何直观想象有理有据,使空间想象力合乎理性、有逻辑.其次, 准确把握几何体的结构特征.数量关系是空间结构不可或缺的重要组成部分,无非是我们眼睛不能直视,需要我们进行抽象概括,然后以纯粹的形式进行演算、推理与证明.因此,在解决立体几何题时,既要挖掘隐含在几何体中的数量关系,又能从数量关系中推断几何特性.最后,重视从动态思维审视几何体.由于几何图形为了直观性,图形中数量有“失真”,其中的一些数量从表面上看与真实的数量并不相符,直接影响对几何体的正确认识和理解.可以通过“拆”解几何体,将空间图形转化为平面图形,为数形结合提供良好的环境[1].