数形结合在初中数学函数问题中的妙用

张西欣

(日照市新营中学,山东 日照 276800)

数形结合在初中数学函数问题中发挥着重要作用,特别是在求实数根和取值范围方面,通过运用数形结合的方法,学生可以将抽象的数学问题转化为具体的图形问题,并通过观察图形的特性解决问题[1].数形结合在初中数学函数问题中的妙用不仅能帮助学生解决问题,还能够提高学生对数学的兴趣.数形结合为学生提供了更加直观、形象的思维方式,使学生能够更好地理解和掌握数学知识[2].

1 求实数根类型的函数问题

在求实数根的问题中,数形结合能够帮助学生直观地理解方程与函数图象之间的关系.例如,在解决方程实数根问题时,可将方程实数根问题转化为函数图象的交点问题,通过观察图象与图象相交的点得到方程的实数根.在这类问题中,常常会出现“是否有实数根”“有几个实数根”“实数根的取值”等问题[3].数形结合通过将抽象的方程问题与具体的图形联系起来,不仅能够提高学生的空间思维能力,还能使学生更加深入地理解抽象概念.

例1 已知x1、x2、x3为方程x3+3x2-9x-4=0的三个实数根,则下列结论一定正确的是( ).

A.x1x2x3<0 B.x1+x2-x3>0

C.x1-x2-x3>0 D.x1+x2+x3<0

图2 等式左右两侧函数

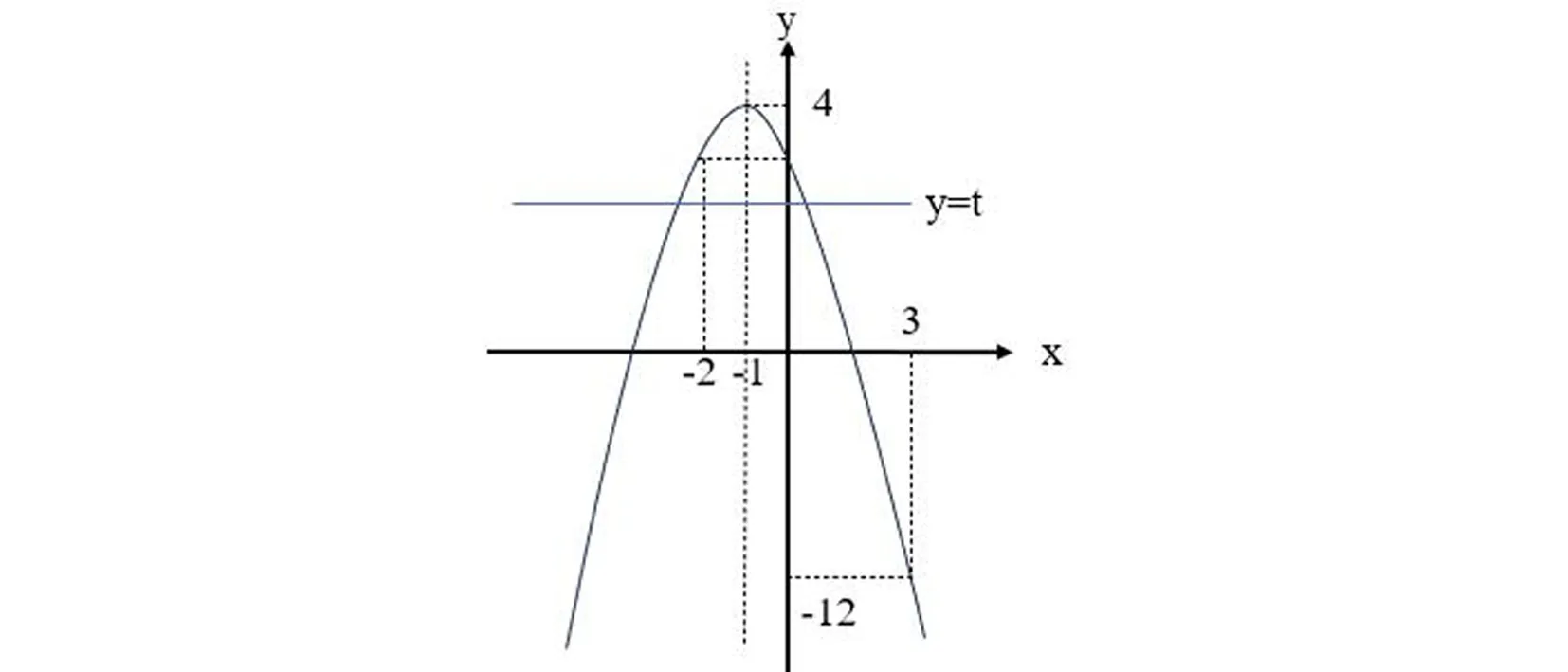
图3 直线与抛物线相交

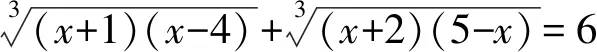
A.0 B.1 C.2 D.大于2

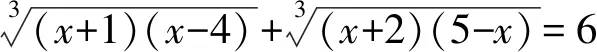
点评本题可以转化为两个函数图象求交点的问题,与例1类似.巧妙之处在于化简之后发现,含变量部分的系数和次幂均相等,这意味着整理后的两个函数图象“仅存在上下平移”.需要注意的是,只有“上下平移”的时候,两函数图象才无交点,存在其他形式平移时,该推理不成立.

2 求取值范围类型的函数问题

在求取值范围的问题中,数形结合可以帮助学生直观地理解函数的定义域和值域.通过将函数的定义域和值域与函数图象对应起来,学生可以通过观察图形的特性来确定函数的取值范围[4].这种直观的方法不仅能够提高学生对函数性质的认识,还能够培养学生的几何直觉和图象处理能力.通过利用函数图象表示函数的变化规律,学生可以理解函数的增减性、极值和最值等性质.

例3抛物线y=-x2+bx+3的对称轴为直线x=-1,若关于x的一元二次方程-x2+bx+3-t=0(t为实数),在-2

A.-12

C.-12

解析方法1:因为抛物线y=-x2+bx+3的对称轴为直线x=-1,所以b=-2,y=-x2-2x+3;此时一元二次方程-x2+bx+3-t=0的实数根可以看作y=-x2-2x+3与函数y=t的图象有交点,如3所示.

因为方程在-2

方法2:因为抛物线y=-x2+bx+3的对称轴为直线x=-1,所以b=-2,此时一元二次方程-x2+bx+3-t=0的实数根可以分情况讨论,设f(x)=-x2-2x+3-t,如图4所示.

图4 一元二次函数有实数解的3种情况

(1)有两个根:即f(-1)>0;f(-2)<0;f(3)<0,此时有4-t>0;3-t<0;-12-t<0;

(2)和(3)有一个根:f(-2)·f(3)<0,此时(3-t)(-12-t)<0.

从而可得-12

点评 本题根据给出的对称轴求出函数解析式为y=-x2-2x+3,可将一元二次方程-x2+bx+3-t=0的实数根可以看作y=-x2-2x+3与函数y=t图象的交点,再由-2

例4已知抛物线C:y=x2-2bx+c.

(1)若抛物线C的顶点坐标为 (1,-3),求b、c的值;

(2)当c=b+2,0≤x≤2时,抛物线C的最小值是-4,求b的值;

(3)当c=b2+1,3≤x≤m时,x2-2bx+c≤x-2恒成立,求m的最大值.

解析(1)因为抛物线C的顶点坐标为 (1,-3),所以y=(x-1)2-3=x2-2x-2,所以-2b=-2,b=1,c=-2.

(3)当c=b2+1 时,抛物线C的解析式为y=(x-b)2+1,如图5所示,抛物线C的顶点在直线y=1上移动:

图5 抛物线与直线

当3≤x≤m时,x2-2bx+c≤x-2恒成立,则可知抛物线C的顶点坐标为 (3,1),设抛物线C与直线y=x-2除顶点外的另一个交点为M,此时点M的横坐标即为m的最大值.

点评本题第(1)问根据已知点的坐标代入解析式确定系数即可;第(2)问先根据已知条件确定抛物线的对称轴,再分段讨论抛物线在各段上取最小值时b的值;第(3)问需运用数形结合的思想,通过抛物线图象的移动范围确定.

总之,数形结合在初中数学函数题中的妙用是不可忽视的.数形结合不仅可以帮助学生直观地理解抽象概念和解决问题,还能够激发学生对数学的兴趣和求知欲[5].因此在今后的教学中,教师应注重数形结合的应用,通过提供具体的图形来引导学生解决数学问题,激发学生对数学的兴趣,培养学生的几何直观.