基于铁木辛柯梁理论的工字梁剪切变形计算方法研究

辛育霞，王勇，付佳豪，倪天琦，齐贺阳

（航空工业北京长城计量测试技术研究所，北京 100095）

0 引言

工字梁是一种空腹式杆件，这种截面设计主要通过离形心最远的翼缘抵抗弯曲，利用腹板抵抗剪切，具有强度高、重量轻的优点，是飞机机翼的理想支撑结构［1］，针对工字梁的研究是研究机翼变形的基础。由于机翼中工字梁尺寸相差较大，剪切对不同受力、不同跨高比以及工字梁的不同位置的影响均不同［2］。而考虑剪切时计算复杂，在剪切影响不大时需要简化计算，忽略剪切变形的影响。因此，探究剪切变形对工字梁的作用规律在飞机结构强度领域具有重要的意义［3］。

工字梁弯曲过程中伴随着弯曲与剪切变形，而剪切变形引起的附加应变情况复杂。现有的工字梁计算大多采用的是欧拉-伯努利梁理论，欧拉-伯努利梁理论假设梁中只有弯曲形变，横截面没有产生切应变，变形后横截面依然为一个平面，且始终垂直于中性轴。这种理论忽略了切应变的效果，计算出的梁的变形量低于现实梁的变形量。铁木辛柯梁理论考虑了梁在弯曲变形的同时产生的切应变，梁受力发生变形时，横截面依然为一个平面，但不再垂直于中性轴。由于它考虑了切应变的效果，计算出的梁的变形量接近梁的真实变形量。然而考虑剪切时情况复杂，计算过程较为繁琐，研究表明对于细长梁欧拉-伯努利梁理论可以给出足够精确的结果，所以目前工字梁的计算大多忽略了剪切应变的影响，缺乏对工字梁剪切变形的计算以及剪切对于工字梁变形影响的研究，不利于梁理论在实际工程中的应用［3-5］。

因此，本文首先选取了基于铁木辛柯梁理论的计算方法，考虑工字梁中剪切变形的影响，通过给出剪切对工字梁变形的影响，提出需要考虑剪切变形的情况。其次，内力的力学性能参数需要开展电测法实验确定，通过理论与仿真以及试验对比梁截面的内力，证明了基于铁木辛柯梁理论的工字梁剪切变形计算方法的有效性。

1 基于铁木辛柯梁理论的工字梁变形计算

针对典型的工字悬臂梁结构，利用铁木辛柯梁理论进行计算［6-8］。

1.1 模型建立

如图1（a）所示，建立悬臂工字梁模型，梁的长度为L，梁截面参数如图1（b）所示，其中梁的翼缘宽度为b，腹板厚度为b0，腹板高度为h0，梁的整体高度为h。梁的一端为固定端，限制位移与旋转，另外一端为自由端，自由端受集中力F作用。选择自由端截面中心O作为坐标原点，该原点位于梁的中性轴上，建立坐标系如图1（a）所示。假设材料为各向同性线弹性材料。

图1 工字梁示意图Fig.1 Schematic diagram of I-beam

1.2 内力计算

从自由端取长度为x的一段梁作为分析对象，如图1（c）所示，则梁截面所受的剪力为Fs = -F，弯矩为M = -Fx。材料力学中梁内力的计算公式为式（1）与式（2）［9］。

式中：σx、τxz分别为坐标x处梁截面的正应力与剪应力，MPa；M为工字梁截面所受的弯矩，M =-Fx，Nm；Iy为梁截面对y轴的惯性矩，mm4；Sy*为梁截面上所求剪应力处的水平线以下（或以上）部分面积对中性轴的静矩，mm3；Fs为截面所受的集中力，Fs = -F，N；F为自由端所受的集中力，N；x，y，z为坐标，mm。

梁截面对y轴的惯性矩为式（3）。如图1（b），梁截面所求剪应力的静矩按照该处水平线以上部分面积计算，为式（4）［9］。

将式（3）与式（4）代入梁截面内力的计算公式（1）与公式（2），得到工字梁任意截面的内力

1.3 挠度计算

在得到任意梁截面内力的基础上，利用铁木辛柯梁理论计算工字梁的挠度。在铁木辛柯梁中，正应变与欧拉-伯努利梁结果相同［6］。对于切应变，欧拉-伯努利梁忽略了切应变，而铁木辛柯梁中切应变可以通过切应力与剪切模量得到

式中：E为材料的杨氏模量，MPa；G为剪切模量，MPa；v为泊松比，E =2G（1+v）。

对应变公式进行积分，得到关于x方向与z方向位移的函数。

将式（10）与式（11）代入εxz的表达式中，得到

式（8）与式（12）只与变量x与z有关，联立得到平衡关系式，并分离变量，得到

式（13）左侧完全依赖于变量x，右侧依赖于变量z，所以两侧均等于同一个常数，假设该常数为c0，两侧分别对f（z）和g（x）进行积分，得到

式中：c1与c2均为积分常数。

将式（14）与式（15）代入式（10）与式（11），得到ux与uz的一般形式

常数c0，c1与c2需要利用边界条件确定，固定固支端的位移与旋转，边界条件为

将上述边界条件代入式（19）与式（20），得到c0，c1与c2的值。最终得到利用铁木辛柯梁理论计算的工字悬臂梁z方向的位移为

在欧拉梁中，假设L远大于h与h0，并且假设v= 0，得到欧拉-伯努利梁理论的挠度为

在欧拉-伯努利梁中，悬臂梁的挠度与受力、长度、材料的杨氏模量、截面形状以及x向坐标有关。在铁木辛柯梁考虑剪切变形的情况下，悬臂梁的挠度相比欧拉-伯努利梁多了一项剪切项，因此变形更大，该剪切项除了与欧拉-伯努利梁结果所受影响因素有关外，还与材料的泊松比、z向坐标有关。

2 结果与讨论

利用铁木辛柯理论计算得到工字悬臂梁的挠度，并分析受力、跨高比，不同截面以及相同截面不同位置受剪切变形的影响，为不同位置考虑剪切变形的必要性提供依据。

2.1 计算模型

定义欧拉-伯努利梁中的挠度为uzE，铁木辛柯梁中的挠度为uzT，则工字梁中剪切引起的附加形变为 |uzT-uzE| ，剪切引起的附加变形率为 |（uzT-uzE）/uzE| 。选取算例，材料参数以及截面参数如表1所示。

表1 工字梁模型参数Tab.1 I-beam model parameters

2.2 受力对剪切变形引起的附加变形影响分析

根据式（19）以及式（20）计算得到附加变形与附加变形率的表达式

由式（21）可知，附加变形与所受集中力F为线性关系，受力越大，附加变形也越大。由式（22）可知，附加变形率与受力大小无关，只与工字梁的形状以及所求位置有关。

选取工字梁的长度L= 1 400 mm 进行计算，在F不同的工况下计算得到梁截面中性轴的挠度。图2 给出了F不同时剪切引起的附加变形。剪切引起的附加变形随着受力增加变大，剪切引起的附加变形与梁截面与固定端之间的距离成线性关系。因此，在其他因素保持不变，只有F变化时，可以根据附加变形判断是否需要考虑剪切的影响。

图2 F不同时剪切引起的附加变形Fig.2 Additional deformation caused by shear at different forces

2.3 跨高比对剪切变形引起的附加变形影响分析

选取受力状态F= 1 000 N，工字梁截面尺寸保持不变，改变长度，选取长度为1 400、1 000、600、200 mm 四种长度的工字梁进行计算，其对应的跨高比L/h分别为14、10、6、2，针对不同跨高比的工字梁进行分析。

图3给出了不同跨高比的梁剪切引起的附加变形，剪切引起的附加变形与截面和固定端之间的距离之间的线性关系不变，且斜率基本不变。

图3 跨高比不同时剪切引起的附加变形Fig.3 Additional deformation caused by shear at different span-depth ratios

图4给出了不同跨高比的梁剪切引起的附加变形率。剪切引起的附加变形率在固定端最大，在靠近固定端的一段范围内急剧减小后趋于稳定，在自由端达到最小值。在靠近固定端的一定范围内，剪切引起的附加变形率可达到100%，随着跨高比的减小，在固定端的附加变形率会更大，因此固定端一定范围内的的计算应充分考虑剪切的影响。在跨高比L/h= 5 时，剪切造成的附加变形率在自由端最小，为10.33%，在靠近固定端的梁中附加变形率逐渐增加，此时剪切造成的影响已经不可忽略。

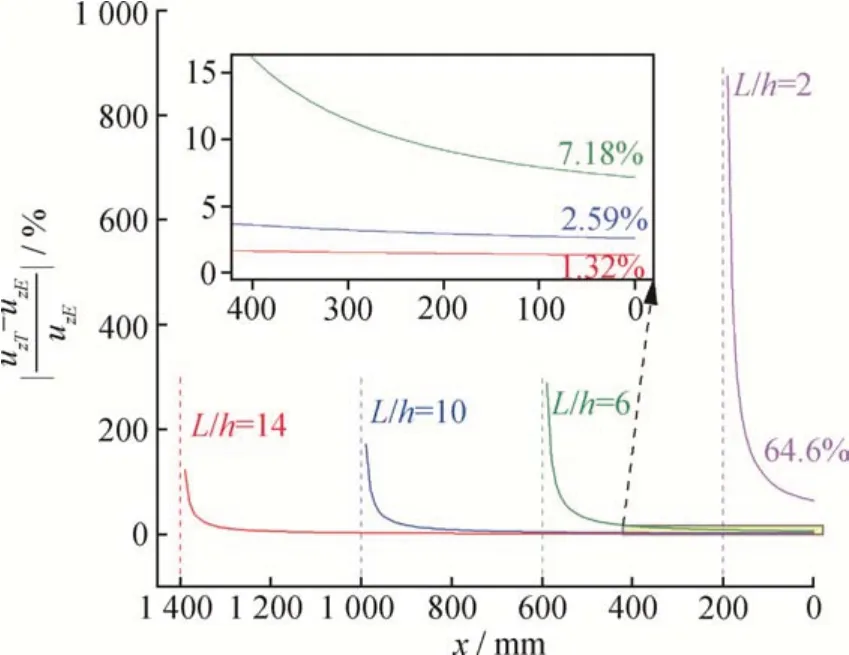
图4 跨高比不同时剪切引起的附加变形率Fig.4 Additional deformation rate caused by shear at different span-depth ratios

2.4 截面内剪切变形引起的附加变形影响分析

选取梁的长度L= 1 400 mm 以及受力状态F=1 000 N 进行计算，针对剪切对工字梁截面内离中性轴不同位置的影响。

图5给出了不同截面以及截面内不同位置剪切引起的附加变形率，在同一个梁截面，剪切对中性轴影响最小，对梁表面影响最大，越靠近固定端，剪切对梁截面不同位置的的影响差异越大。

2.5 工字梁仿真与验证

选取工程中的典型工况，利用Abaqus 进行有限元仿真，梁的长度L= 1 400 mm，梁受集中力F= -1 000 N，截面参数与理论计算相同，材料为304 钢。梁的边界条件为一端固支，一端受集中力。在Abaqus中，选用不同类型的网格进行计算，梁单元B33 忽略了剪切作用，用于模拟欧拉-伯努利梁，B31 允许剪切变形，用于模拟铁木辛柯梁。图6给出了是否考虑剪切得到的工字梁挠度的理论与有限元解，有限元与理论结果基本一致，验证了本节理论结果在工程中的可行性。

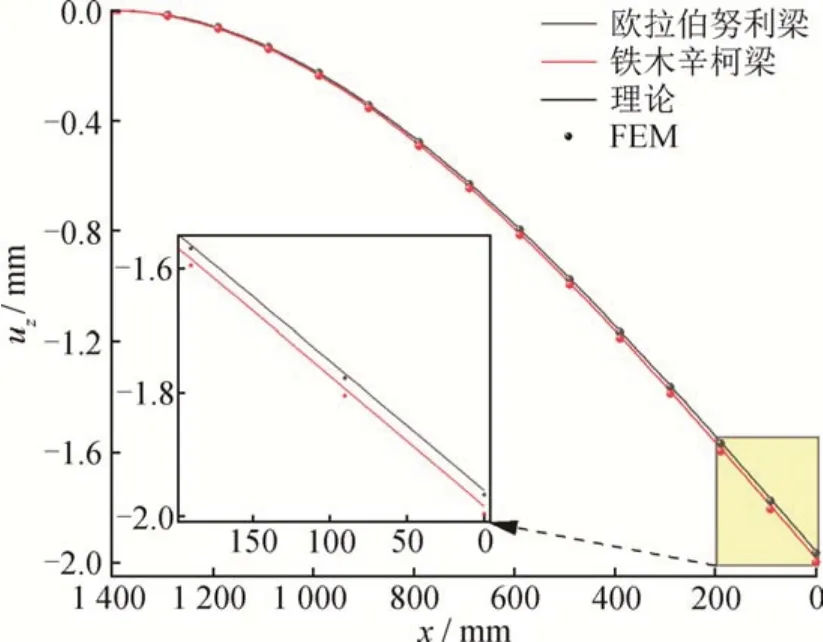
图6 工字梁挠度Fig.6 I-beam deflection

图6 结合图2 可以看出，在细长梁的实际应用中，根据欧拉梁和铁木辛柯梁理论得到结果相差不大。在工程实际应用中，可以根据所需计算精度要求，判断是否需要考虑剪切的影响，大部分情况下仍然可以用欧拉梁理论进行描述计算。根据图4，在短梁中由于结果相差较大，应该根据实际情况判断是否需要考虑剪切的影响。

3 基于电测法的工字梁内力测试

为获得实际工程中的内力值，需要开展电测法实验，为理论结果提供支撑。并利用Ansys 进行有限元仿真，得到有限元（Finite Element Method，FEM）结果，并与第一节中的理论值进行对比分析，得出相关结论，证明该理论方法的有效性。

3.1 试验材料与设备

如图7所示，试验需要用到的试验设备有工字梁、应变片、承重框架结构、数据采集系统、载荷加载系统等［10］。

图7 试验原理示意图Fig.7 Schematic diagram of test principle

选取机翼中工字梁的典型尺寸设计制作工字梁。工字梁翼缘宽度70 mm，整体高度100 mm，腹板厚度4 mm，结构材料为304钢。

3.2 布片位置与方式

应变片在工字梁上的布片位置以及布片方式如图8所示。选择三个测试切面1、2、3，在任意测试切面上，在工字梁的上下翼缘分别布置2 个单片用于测弯矩，在工字梁腹板的两侧布置2 个人字片用于测剪力。加载点位于梁自由端，通过在自由端施加集中力实现工字梁的变形。如图9 所示，本次试验采用组惠斯通全桥的方式，提高试验精度[11]。

图8 工字梁布片示意图Fig.8 Schematic diagram of strain gauge distribution on I-beam

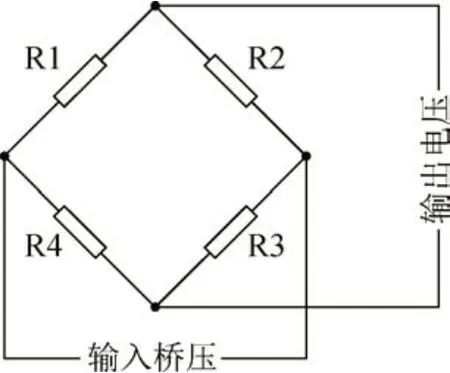
图9 惠斯通电桥Fig.9 Wheatstone bridge

3.3 试验加载与数据处理

选择合适的高度将工字梁通过螺栓连接的方式［12］，固定在承重框架上。通过承重框架上的地轨将伺服作动器固定在承重框架上，根据加载需求调整固定位置。通过伺服作动器上的力值传感器［13］、控制器和笔记本控制伺服作动器作用在工字梁上的载荷大小。

本次试验数据采集系统由KAM-500 数据采集器、接线盒、电源盒、笔记本等组成。电源盒为数据采集器提供稳定的激励电压，应变片组桥后连接到接线盒上。数据采集器输出的信号经处理后在笔记本上生成试验结果。

3.4 试验与数据处理

本次试验分为1 000、2 000、3 000 N 试验测试。加载过程为逐级加载后逐级卸载，在1 000 N试验中，力的变化幅度为200 N；在2 000 N与3 000 N 试验中，力的变化幅度为500 N。为避免试验过程中的偶然误差［14］，每组试验都重复进行3 次，按3 次平均计算。若发现某一点数据异常，本次试验重做。

数据处理过程中只保留加载部分的试验数据，对3 次试验取平均值。表3 为3 次试验最大载荷对应的数据采集系统的输出码值，M1、M2、M3分别为测试切面1、2、3 测试得到的弯矩对应的码值；Q1、Q2、Q3分别为测试切面1、2、3 测试得到的剪力对应的码值。

表3 原始数据记录Tab.3 Original data record

根据采集器说明，得到的码值结果为模数转换器输出的二进制码值，该码值除以3.28 转换为对应的应变值。在惠斯通电桥中，得到的信号是放大4 倍的信号，因此，输出的应变值除以4 为该截面的真实应变。

3.5 工字梁仿真

在Ansys 中建立工字梁模型进行仿真，选取与试验相同的工况与材料进行计算。由1.1节的理论结果可以得到结论，截面表面的正应力在靠近固定端的过程中会逐渐增大，且正应力与坐标成线性关系。随着集中力增大，同一截面的应力增加。对于截面剪力，当F相同时，剪力在不同的截面相同，与x无关，只与z相关，截面内的剪力在中性轴达到最大值，向两侧逐渐衰减［15］。

将仿真与试验结果与理论结果对比，如图10、图11所示，理论、仿真均与电测法结果基本一致，证明了该计算方法的有效性。

图10 工字梁表面正应力Fig.10 Normal stress on surface of I-beam

图11 工字梁中性轴剪力Fig.11 Neutral axis shear force of I-beam

4 结论

本文首先利用铁木辛柯梁理论计算工字梁的内力与挠度。结果表明，考虑剪切作用得到的挠度更大，比忽略剪切作用的方法多了一项剪切项，在悬臂梁靠近固定端的一段距离内剪切影响很大，并且在跨高比小于5 时，剪切造成的影响可达到10%，此时剪切不可忽略，应充分考虑剪切的影响。随后通过电测法进行工字梁弯曲试验。结果表明，利用该测量方法得到的结果与理论以及有限元结果基本一致。本文构建的利用铁木辛柯梁计算的工字悬臂梁模型，是一种能够为飞机中工字梁的计算提供更加符合真实情况的模型，能够应用在实际工程计算中。