声学高温计拓扑结构优化研究

赵乂鋆，赵俭，陈鑫虎

（航空工业北京长城计量测试技术研究所，北京 100095）

0 引言

随着对极端环境测温需求的提高，测量诸如高温风洞试验段和航空发动机燃烧室等高温、高流速的气流温度场环境的需求也日渐攀升［1］。这类测温环境中，有着气流场复杂、温度场变化速度快、环境干扰强等特点；甚至部分环境会因密封和防辐射等问题，无法将敏感元件直接浸入到待测气流场中。复杂多变的气流温度场使得采用传统的热电偶等接触式测温方式时间常数较大、不耐腐蚀和辐射等问题被放大，不能很好地满足高温、高流速的气流温度场环境的测温需求［2］。而声学测温作为一种较新的测温方法，具有抗腐蚀、抗振动、测温范围广等特点，逐渐受到各国研究人员的重视。本文的主要研究内容是非接触式的声学测温方法。

从原理上来说，非接触式的声学测温方法大致有声速法测温、声共鸣法测温以及声频率法测温等［3-5］。在气流温度测量中，声速法测温与声共鸣法测温的研究与应用更成熟。这两种方法最基本的原理都是通过测量声音在气流场中的传播时间，进而反算出声波传播路径上气流温度场的平均温度，再根据解耦和插值等算法得出温度数值或是其他相关参数。其中，声共鸣法测温更加关注温标的建设与准确度；声速法测温更加关注气流平面温度场的还原。因此，在对气流温度场进行测量与还原时，首要应考虑运用声速法测温，进行声学高温计的研究。

国内的声学高温计相关研究始于20世纪末［6］。时至今日，声学高温计在炉膛等温度较高、气流速度不快的封闭空间温度测量上取得了较为成熟的研究成果［7-12］。当温度升高时，声探头振动的感受部分会受到高温影响会导致性能下降，直接影响到发射和接收声信号的完整程度，进而影响到温度的测量；此外，声波在高流速的气流场传播时，会在矢量合成的作用下明显改变传播方向，使得预计的声波传播距离和实际的声波传播距离产生差异，增大声学高温计的测温误差。当气流温度进一步升高，速度进一步加快时，气流温度场的测温环境将会变得更加恶劣。根据之前的研究［10］，目前现有的一套声学高温计在600 ℃，0.2 Ma 的情况下，现有声学高温计的中心区误差为2%。但当温度和气流马赫数上升时，中心区的误差可达20%以上，且一段时间内，还原的中心温度差值可达理论数值的40%，严重影响了温度场还原的精度和准确性。

针对以上声学高温计在高温、高流速等极端环境测温中存在的普遍问题，采用仿真的方式对声波传播路径在极端环境中的变化情况进行模拟。以现有的一套声学高温计装置为基础模型，设置与变化情况匹配的声探头拓扑结构并在模拟环境中对发射与接收的声信号参数进行仿真优化，提高测温稳定性和精度。

1 声学高温计基本原理

现有声学高温计装置的核心测温原理是非接触式声学测温中的声速法测温。温场中的声速由一维微元运动公式［13］推导得出。

式中：c为温场中的声速；γ为被测介质的绝热状态指数；R、M分别为摩尔气体常数和气体摩尔质量；T为热力学温度；Z 为常数，若被测介质是空气，一般值取为20.05。

在已知声波穿过待测温场路径长度的情况下，为了得到温场中的声速c，需要获取声波在温场中的传播时间。声波传播时间可由互相关法计算得到。在直接进行互相关计算之前，需要对接收到的声信号进行包络提取，目前常用的方法为希尔伯特变换法。希尔伯特变换法即通过希尔伯特变换求得获取到的声波信号包络［14］，即

式中：̂(t)为连续时间信号x（t）的希尔伯特变换；t为时间；*为卷积运算符号；j为复数符号；y（t）为x（t）的信号包络。

获取包络之后，便可以通过计算机软件准确计算出声波的传播时间，进而获得声速。当被测介质的浓度和成分稳定时，气体摩尔质量为常数，Z 为定值。从式（1）中可得，声速c和温度T在理想情况下是单值对应关系。以此得到该声波路径上的平均温度。

当多条声波路径上的平均温度已知时，即可通过矩阵解耦算法计算得出特定区域的平均温度。常用的矩阵解耦算法是最小二乘法。最小二乘法的基本原理是将整个待测平面划分为若干相同的像素，再根据声速与温度的关系计算出每一个像素的平均温度，最后用插值的方式还原整个温度场［15］。现有声学高温计装置中使用的最小二乘法基本原理如下：

首先，每一条声波沿着其传播路径传播时间t都可以表示为

式中：a为空间状态因子，表示穿越气流温场的平均声速c的倒数，ds表示声波传播路径长度的微分值。

接着，给每一条路径和每一个像素编号，令ΔSk，i表示第k条路径通过第i个像素的长度，ai表示第i个像素的声波平均传播速度c的倒数，根据式（3）可知理论上声波在第k条路径的传播时间tk为

通过实验测得的声波传播时间为tc，则可计算出声波传播时间的误差εk为

然后，利用极值求解的方法使误差εk的平方和最小，得到一个含参数的正则矩阵。当声探头的位置和数量固定时，正则矩阵参数为常数。当矩阵可逆时，可得空间状态因子矩阵A。又由于空间状态因子是声波传播速度的倒数，则可以得到每个像素内的区域平均温度为

最后，利用适当的插值算法，就可以重建出整个待测平面温度场的分布。

2 仿真参数设置

2.1 仿真分析背景

在利用声波传播时间计算气流温度时，变化的气流速度会导致声信号的声压级降低。一般来说，声压级越高，声信号的能量就越强，声压的幅值也越大，受到环境干扰的影响就越小。加上环境干扰的影响，声探头获取的声源信号会产生变形。变形声信号会影响声波在气流场中传播时间获取的稳定性和精度，进一步使气流温度场还原的精度以及可靠性降低。根据矢量叠加的原理可知，声波在气流中传播时，实际的传播方向为声波矢量与气流矢量的叠加方向。现有声学高温计装置的声探头在同一水平面上，倾斜的声波传播方向势必会导致接收到的声信号声压级减小，更易受到环境干扰。因此，需要从硬件角度寻找并设计一种适用于当前研究指标的声探头拓扑框架，提高声学高温计测温的精度和可靠程度。

本文设置不同分布半径和不同朝向夹角的声探头支架作为仿真分析的基础模型。以Virtual.Lab为仿真软件，通过设置恒温度不同马赫数以及恒马赫数不同温度的两类条件分别对不同结构的声探头支架进行声压级降低的仿真分析。通过仿真的方式寻找出最佳的声探头支架拓扑结构。

2.2 声探头结构的仿真建模及环境设置

为了分析声探头朝向对接收声信号的影响，在仿真中分别设置了以15 cm 和20 cm 为直径的两种声探头支架。每一种直径的支架又分别设计了发射声探头与接收声探头朝向正对、探头朝向与支架平面夹角15°、30°以及45°的情况，总计8 种声探头的支架。以直径和探头夹角的方式命名，中间用短横线进行连接。如“15-dir”表示15 cm直径探头朝向正对的声探头支架，“15-15”表示15 cm 直径探头朝向与支架平面夹角15°的声探头支架。以15 cm 直径的声探头支架为例，在Virtual.Lab 中建模并简化其他非必要构件后，部分15 cm直径声探头支架Virtual.Lab模型如图1所示。

图1 部分15 cm直径声探头支架Virtual.Lab模型Fig.1 Partial 15 cm diameter acoustic probe support model in Virtual.Lab

仿真采用有限元仿真的方式进行。将声探头模型放入到圆柱形分析环境中模拟气流通过部分并网格划分，得到需要进行分析的有限元分析三维网格划分，如图2所示。

图2 有限元分析三维网格划分剖面图Fig.2 3D mesh division profile of finite element analysis

最后对建立的网格进行声环境以及边界条件设置，增加监控声压变化的场点，如图3所示。至此完成不同声探头结构的仿真建模及环境设置。

图3 增加场点及边界条件的有限元分析模型Fig.3 Finite element analysis model with field points and boundary conditions

3 仿真结果与分析

3.1 恒温度不同气流速度下各声探头支架仿真情况

为了分析各声探头支架在不同气流速度下的各不同方向上声压级降低情况，设置恒温度不同气流速度的仿真条件。其中，设置环境温度为常温，气流速度以0.1 Ma为间隔，最大值为0.3 Ma。由于同一种探头支架内还存在多个声波接收点。故在分析时分别将正对方向、偏斜22.5°、偏斜45°的声压级变化情况命名为“正对方向变化情况”、“侧对方向变化情况”、“边缘方向变化情况”，以此为分类计算不同声波接收探头处的声压级占比声波发射处声压级的比值。其中，两种声探头支架在0.2 Ma气流速度下的声压级分布示意图如图4所示。

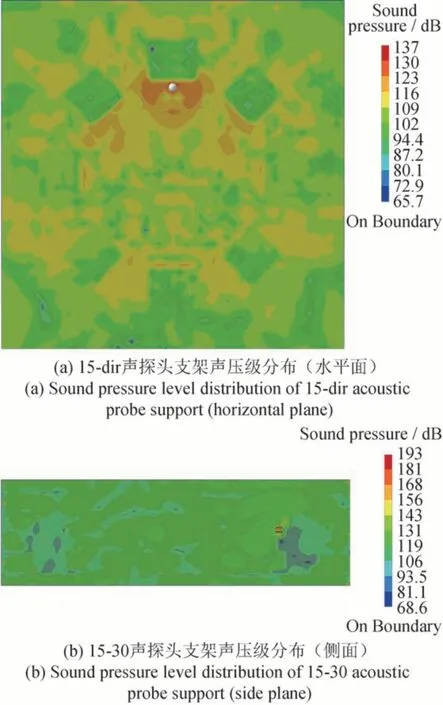
图4 部分声探头支架0.2 Ma流速下声压级分布示意图Fig.4 Schematic diagram of sound pressure level distribution at a flow rate of 0.2 Ma for some sound probe supports

以声探头发射点的声压级为标准，仿真计算并记录不同声探头支架不同方向上的声压级数值，令传播后的声压级数值与发射点的声压级数值相比作为声压级衰减的评判标准，将各个声探头支架在恒温不同流速情况下的声压级的衰减情况进行汇总，得到的数据如表1所示。

表1 各声探头支架在不同气流马赫数下接收声压级占声源声压级比值Tab.1 Ratio of received sound pressure level to source sound pressure level of each acoustic probe support at different airflow Mach numbers

表1中记录在不同声探头支架内径中，不同支架类型常温环境下分别在0.1、0.2、0.3 Ma 时不同声探头偏斜角度的声压级减小情况。由表1分析可知，当气流速度逐渐增大时，正对朝向的声探头支架的声压级分布的均匀性和对称性越差，且声压级减小的程度越大。说明在气流速度增大时，正对朝向的声压级会受到气流速度变化带来的较为明显的影响。

此外，当气流速度逐渐增大时，倾斜角度的声探头支架的声压级并未像正对的声探头支架一样逐渐下降，而是存在上升后又下降的趋势。对于直径15 cm 的声探头支架组而言，除了15-45 声探头支架之外，总体上满足正对方向上的声压级分布情况较侧对方向以及边缘方向较好；侧对方向上的声压分布较边缘方向较好的特征。三个方向上，声压级变化基本符合先增大后减小的趋势。

经由先前的研究［10］可知，声探头的声波接收范围存在角度限制。当探头的距离相同时，声探头发射与接收口之间对得越正，声压级的减小情况就越小。反映在15 cm 直径上的声探头支架上时，正对方向上的声探头之间相对距离最远，但因为朝向正对，使得声探头的声源信号有较大区域的接收口。因此正对方向上的声压级减小得少。与之相对的，边缘方向上的声压级减小要多得多。大体上与仿真结果相符。

以15 cm 直径声探头支架为例，若以矢量合成的计算方法可知，当声速恒定的情况下，气流在0.1～0.3 Ma 时分别传播了1.5、3.0、4.5 cm。将气流传播的距离与探头朝向的距离进行对比可知，在0.1 Ma 时，正对、侧对和边缘方向上的气流传播距离与15-15 和15-30 声探头支架的偏斜角度较为靠近，体现为两声探头支架三个方向上声压级衰减较小，但总体上相差并不大；当气流马赫数升高时，气流传播的矢量距离变长，有一定倾斜角度的声探头支架与合成后的声波实际传播方向更为接近。具体表现为在气流马赫数上升，环境干扰更强，整体声压级衰减增大的情况下，15-15和15-30 声探头支架的整体声压级减小相比其他声探头支架要小得多，这与仿真结果是相符合的。值得注意的是，在边缘方向上，由于声波传播的距离过短，其声矢量和气流矢量合成后的角度大致为40°，与仿真结果中在15-30 和15-45 声探头支架边缘方向上的声压级衰减情况相符。至于15-45声探头支架在侧对方向上相较于正对和边缘声压级均较小的情况，推测可能是由于倾斜角度过大，导致仿真并未准确解算出实际矢量合成后的声压级减小情况。

总体来说，在直径15 cm 的声探头支架组内部，15-30 的声探头支架在各个流速情况下均有较好的声压级分布和较小的声压级减小，综合各个流场下的声压级分布较优。

对于直径20 cm 的声探头支架组而言，正对方向上的声压级占比情况较侧对方向略高，较边缘方向更高。呈现出较为明显的3 层分布趋势。同时，3 个方向上的声压级随着气流温度改变而波动降低。

以相同的方法对20 cm 的声探头支架组分析可知，当声探头支架的直径增大时，气流在不同马赫数下传播矢量长度不变。因此在声探头直径增大时，声矢量与气流矢量合成的角度相较于15 cm声探头支架而言会变小，体现在声压级变化上则表现为20-15 与20-30 声探头支架的声压级之差比15-15 与15-30 声探头支架的声压级之差小，符合仿真结果的规律。

综合对比直径20 cm 的声探头支架组的声压级减小情况，20-30 的声探头支架综合各个流场下的声压级分布较优。

综合比较15-30 以及20-30 两个声探头支架的声压级分布情况。15-30 的声探头支架有着更好的声压级分布以及较少的声压级减小。当气流速度较快时，20-30 声探头支架的声压级受气流速度影响产生的变化相较于15-30 声探头支架更为明显。经过之前的计算分析，推测在相同的声探头倾斜角度下时，较长的传播路径会增大对声压级较小的影响。此外，20-30 声探头支架侧对方向以及边缘方向的声压级减小情况明显比15-30 声探头支架大，这也有可能是受到相同因素的影响。故综合比较可知，当恒定气流温度改变马赫数时，15-30声探头支架的结构更优。

3.2 恒马赫数不同气流温度下各声探头支架仿真情况

为了分析各声探头支架在不同气流温度下的各不同方向上声压级降低情况，按照同样的方式，设置了恒马赫数不同气流温度的仿真条件。其中，设置马赫数恒为0.3 Ma，气流温度分别为500、700、900 ℃，对各声探头支架的声压级降低情况进行分析，部分结果如图5所示。将各个声探头支架在恒马赫数不同温度情况下的声压级的衰减情况进行汇总，得到的结果如表2所示。

表2 各声探头支架在不同气流温度下接收声压级占声源声压级比值Tab.2 Ratio of received sound pressure level to source sound pressure level of each acoustic probe support at different temperatures

表2中记录在在不同声探头支架内径中，不同支架类型分别在恒流速时，500、700、900 ℃下不同声探头偏斜角度的声压级减小情况。

当气流马赫数恒定时，声速随着温度的升高而变大，而气流的实际传播速度也随着温度的增大而增大。实际上，当气流马赫数恒定时，声矢量与气流矢量的合成矢量方向是确定的。对15 cm的声探头支架组而言，经过矢量合成的计算可知，正对方向、侧对方向和边缘方向上的总体倾斜角度在10° ～ 30°之间。也即是从理论计算上来说，声压级分布情况较优的支架应为15°或30°角倾斜的声探头支架。

对表2 中的数据进行归纳可知，对于直径15 cm 的声探头支架组而言，总体上满足正对方向上的声压级分布情况较侧对方向以及边缘方向较好；侧对方向上的声压分布较边缘方向较好的特征。正对方向以及侧对方向声压级变化基本符合先增大后减小的趋势，而边缘方向的声压级符合先减小后增大的波动趋势。15-15 和15-30 两声探头支架确实具有相对较小的声压级减小情况，与理论分析的结果大致符合。总体来说，在直径15 cm 的声探头支架组内部，15-30 的声探头支架综合各个流场下的声压级均在0.820及以上，对于不同温度情况下的气流场适应性较好。

对于直径20 cm 的声探头支架组而言，正对方向上的声压级分布情况与侧对方向相当，较边缘方向较好。正对方向并无明显的随着气流温度改变而变化的规律，而边缘方向的声压级符合总体上升的趋势。

同理，根据上面20 cm 声探头支架的分析以及3.1 节中的总结。可以计算出矢量合成的角度在正对方向、侧对方向和边缘方向上的总体倾斜角度6°～20°。与3.1 节中20 cm 声探头支架在倾斜角度的分析上相符。也即从理论分析上来说，20 cm 声探头支架组中，20-15 声探头支架在理论上会获得更好的声压级分布情况。通过对比表2 中20 cm 声探头支架组在各方向上的声压级减小情况可知，理论分析与仿真的结果基本相符。20-15 的声探头支架综合各个流场下的声压级在0.83 及以上，其声压级相较于同组其他声探头支架而言分布较优。

综合比较15-30 以及20-15 两个声探头支架的声压级分布情况。15-30 的声探头支架有着更好的声压级分布以及较少的声压级减小，但其受温度影响产生的变化相较于20-15 声探头支架更为明显。当气流温度较高时，20-15 声探头支架的声压级减小情况明显比15-30 声探头支架小。即当恒定马赫数改变气流温度时，20-15声探头支架的结构更优。

由3.1 与3.2 中的分析可知，15-30 和20-15 分别在恒温变马赫数及恒马赫数变温的测温环境中表现最好。对比两种声探头拓扑结构，虽然20-15 声探头支架在恒定马赫数情况下时要比15-30 声探头支架更好，但15-30 声探头支架在恒定温度时得到声压级减小以及分布情况要比20-15 声探头支架好得多。因此，从仿真的声压级减小结果而言，15-30 声探头支架相对来说是最优解。若从给声探头支架增加冷却管或防止声探头的端口处因高温融化等加工或实际试验的可靠性角度考虑，也可将20-15声探头支架作为声探头拓扑结构的备用选项。

4 试验测试

为了实际测试不同声探头拓扑结构对测温精度和稳定性的影响，将试验环境设置为300 ℃，0.2 Ma 的气流，设计了15-dir、15-30、20-15 三个声探头支架作为对照试验组进行对比。由于试验环境中的干扰过多，对声信号的声压级测量会受到较大的气流环境噪声干扰，因此以1 min 内三个方向上测得的声波飞渡时间数据为依据，计算其样本标准差、平均值与理论数值的差值和理论数值的比值（相对误差比值），分别考察不同声探头拓扑结构在三个方向上的测温稳定性和精度。样本标准差越低，稳定性越好；比值越低，精度越高。得到的数据结果如表3及表4所示。

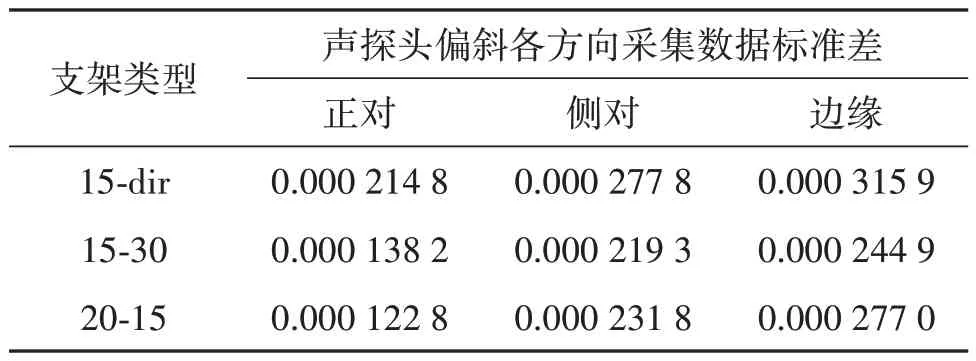
表3 三组声探头结构采集数据标准差Tab.3 Standard deviation of data collected from three acoustic probe structures

表4 三组声探头结构采集数据相对误差比值Tab.4 Relative error ratio of data collected from three acoustic probe structures

根据第2节中的分析可知，声压级的变化反映了当前声信号传播能力在气流温度场的变化情况。当声信号幅值受环境影响降低时，接收声信号波形越光滑，包络提取和互相关计算也越准确，因此声压级的减小越少，采集数据的标准差和相对误差比值也越小。故通过仿真获取的声压级变化趋势在理论上应当与试验时采集数据的标准差和相对误差比值的变化趋势相同。从表3 及表4 中可以看出，反映数据波动情况的标准差和数据精度的相对误差比值的变化趋势大致相当。在正对方向上，采集获得数据的精度和稳定性最好。侧对方向上要稍差一些，边缘方向上的情况最差。

在三个对照试验组中，正对方向上数据精度和稳定性最好的是20-15 声探头拓扑结构，其次是15-30 结构，该特征与仿真计算的结果一致。根据第3 节的分析，应当是20-15 声探头拓扑结构的角度更加靠近实际矢量合成角度的缘故；侧对和边缘方向上，15-30 结构比20-15 结构有更小的标准差和相对误差比值，二者比现有15-dir结构均有明显提升。经分析可知，当声信号传播的水平距离变短时，气流矢量的传播距离不变，因此矢量合成后的角度变大，更加靠近15-30 的声探头拓扑结构。此外，20-15 声探头拓扑结构有更长的内径和更多的声信号传播距离，声信号在气流场中的衰减更严重，声信号传播的稳定性也会受到影响而降低。

以标准差的数值作为评判标准，15-30 在三个方向上的标准差数值总和降低22.4%，20-15 在三个方向上的总和降低17.5%，可知15-30 声探头拓扑结构的综合性能更好。

5 结论

从现有的声学高温计出发，分析了声学测温装置的测温原理，及现有声学高温计存在的测温精度和稳定性问题的原因。提出并构建了将声学高温计中的声探头朝向进行相应的调整，使声波和气流矢量合成之后的实际声波传播方向落在接收声探头敏感区域上的声探头拓扑结构模型。

以LMS Virtual.Lab 声学仿真软件为仿真环境，构建了数个不同的分布直径、不同声探头朝向的拓扑结构。设置好边界条件和流体参数后，对各声探头拓扑结构进行恒马赫数变温度以及恒温度变马赫数仿真计算。总结不同声探头拓扑结构各方向上的声压级减小情况，通过比较分析出15-30和20-15 声探头拓扑结构声压级综合减小均在0.2以下，接收到的声信号强度较高。

根据仿真计算的结果，设计了同工况下现有声学高温计支架与15-30、20-15两种声探头拓扑结构支架的试验。根据试验结果的数据分析可知，在常温至900 ℃、0～0.3 Ma的气流温度场环境中，15-30 声探头拓扑结构的采集数据标准差最小，比现有结构降低了22.4%。明显提升了测温稳定性和精度。

目前的研究仅对气流温度不大于900 ℃，气流速度不高于0.3 Ma 的环境进行了分析和试验，在之后的研究中还需要考虑到随着温度上升以及流速加快带来的压力及声波传播方向变化，进一步提升声学高温计的测温性能。