基于HITEMP数据库的分子吸收光谱高精度快速建模方法
2023-12-07钱宝健蔡静常海涛高一凡
钱宝健,蔡静,常海涛,高一凡
(航空工业北京长城计量测试技术研究所,北京 100095)
0 引言
分子吸收光谱是一种描述物质分子对特定波长光的吸收能力的图谱,通过测量物质对不同波长光的吸收程度,可以推断物质的组成、浓度、结构和化学性质等重要信息,从而在燃烧诊断[1-2]、温度测量[3-4]、污染物监测[5]等领域中进行定性和定量分析。随着应用环境从实验室常压燃烧器向发动机燃烧室等高温高压环境扩展,吸收光谱技术也从双谱线向宽带多谱线发展。目前宽光谱测量技术因可提供更丰富的吸收谱线信息成为燃烧诊断领域的重要发展方向。
Wang 等人提出的同时优化基线和光谱模拟变量的吸收光谱后处理方法实现了O2光谱在9.5 cm-1波数范围内的5 个跃迁温度测量的同步拟合,由于跃迁数量少,在拟合过程中,该方法的简单性使实时光谱模拟成为可能[6]。针对近红外H2O光谱具有的高密度跃迁,美国威斯康辛大学发动机研究中心的JEAN M.SIMMS 等人使用同步优化算法,同时优化温度、展宽和基线共9 个变量,将测量的光谱与光谱数据库相匹配,并确定实验气体温度,在已知条件下的环境室中进行测量,产生的温度读数只有1.47%的误差[7]。德国达姆施塔特工业大学的N G Blume等人发展了超连续宽带激光吸收光谱在燃烧环境中应用的宽带拟合方法,并在WHP 燃烧器中验证了定量测量的准确性[8]。王珍珍等人使用1 335 ~ 1 375 nm 的宽扫描激光器,利用CT-TDLAS 技术成功测量了燃烧器在300 ~ 2 000 K 高温和0.1 ~ 2.5 MPa 高压条件下的空间和时间分布[9-10]。艾苏曼等人数值仿真研究了7 361 ~ 7 485 cm-1范围内的79 条H2O 吸收谱线在300 ~ 2 000 K 温度范围内的直接吸收光谱宽光谱测温的准确性,并模拟验证了光谱参数误差等对于测温精度的影响[11]。
目前针对宽光谱的温度、浓度等测量算法主要通过理论吸收光谱与实验获得的吸收光谱进行最佳拟合,获得温度、浓度等信息,因此这些算法都离不开对于吸收光谱的高精度建模。HITEMP数据库包含大量的高温跃迁谱线,满足分子吸收光谱高精度建模需求,但其庞大的数据量使得高温吸收光谱理论模型难以实现快速计算,更无法应用于需要大量迭代的拟合测量中。因此,本文针对发动机燃烧室等复杂环境温度测量需求,从线型函数的简化、线翼截止准则、谱线数据库的优化三个方面进行基于HITEMP 数据库的分子吸收光谱建模研究,以实现超连续光谱理论吸收模型的准确快速计算,为宽光谱测温算法的实现提供模型基础。
1 分子吸收光谱模型的建立
1.1 分子吸收光谱理论基础
Beer-Lambert 定律作为吸收光谱的核心定律描述了入射激光强度和透射激光强度之间的关系,示意图如图1所示,关系式如式(1)所示。

图1 Beer-Lambert定理示意图Fig.1 Schematic representation of Beer-Lambert law
式中:α(v)为光频率v下的吸光度,I0(v)为入射激光强度,It(v)为透射激光强度。对于单一的典型小分子孤立跃迁,可将吸光度表示为
式中:k(v,T,P,χrad)为吸收系数,L为气体样品的厚度,Sj(T)为温度T下过渡j的线强度,P为气体总压力,n为气体的数量密度,χrad为辐射组分的摩尔分数,ϕj为过渡线形函数。式(3)将光谱吸收系数与气体分子的性质相互联系。
线强度表征了气体分子对光波吸收的强弱,式(4)为简化后的温度依赖的线强度表达式
式中:h 为普朗克常数,c 为光速,温度T处的线强度Sj(T) 可以由分子参考温度T0处的线强度Sj(T0)、吸收分子的配分函数Q(T)、跃迁的低态能量和跃迁的频率v0,j等参数来确定。
配分函数是描述分子或原子系统在给定温度下的能级分布情况的物理量,它与系统的能级结构和温度有关,其值可以用于计算吸收光谱的强度、能级跃迁的概率等相关参数。配分函数被定义为e(-hcEs/kT)对所有状态s的直接求和,计算公式为
式中:di为与状态无关的简并因子,ds为与状态相关的简并因子。高分辨力透射分子吸收光谱数据库(High-Resolution Transmission molecular absorption database,HITRAN)和 HITEMP 数据库[12]提供了每个物质和同位素在70 ~ 3 000 K 温度范围内的总内部分区和(根据 Fischer 等人的计算[13])。实际使用中可以在指定的温度下通过线性插值计算,或在必要时使用HITRAN全局数据外推计算。
线型函数用来描述光谱吸收系数随频率的变化情况,不同的展宽机制使用不同的线型函数来表示,常见的线型函数有:高斯(Guass)线型函数、洛伦兹(Lorentz)线型函数、福伊特(Voigt)线型函数。随着分子光谱学的发展和对于分子跃迁形状高精度表示的要求,出现了如Galatry 线型(GP)、速度依赖的Voigt 线型(SDVP)、以及Hartmann-Tran线型(HTP)等线型函数[14]。
1.2 HITEMP数据库
分子吸收光谱模型的建立需要借助高分辨力的分子光谱数据库,本文使用HITEMP 数据库,HITEMP 数据库是HITRAN 数据库的高温版,目前该数据库包含了H2O、CO2、CO、CH4、NO、NO2、N2O 以及OH 这8 种物质的高温分子光谱信息。最新版本的HITEMP2010数据库提供的每条谱线信息均由160 个字符表示,表1 展示了数据库中H2O 分子在6 400.107 021 cm-1处的数据格式定义及对应的标识符。

表1 HITEMP数据库数据格式参数说明及示例Tab.1 Explanation of data format parameters and examples in the HITEMP database
1.3 逐线计算
吸收光谱的计算模型按照不同的波数间隔计算可以达到不同的建模精度,其中逐线计算模型(Line-By-Line,LBL)精度最高。式(3)为单一跃迁吸收系数的表达式,而物质在某一频率处的吸收系数kv为所有吸收跃迁在该频率处的吸收系数的叠加,如式(6)所示
式中:Xj为物质j的浓度,Si,j(T)和ϕi,j分别为物质j在吸收跃迁i处的线强度和对应的线型函数。
通过式(6)可求得对应吸收物质在某一频率处的吸收系数,乘以吸收路径的长度L后得到对应的吸光度α(v),对应频率的吸光度曲线即为该吸收物质在对应频率范围内的吸收光谱,即完成了吸收光谱的建模。该模型可用于模拟研究不同物质的吸收光谱特性以及用于相关理论计算,如计算单条吸收谱线积分吸光度和宽光谱求解算法中计算理论吸收光谱。
首先通过HITRAN 应用程序接口(HITRAN Application Programming Interface,HAPI)连接HITRANonline 网站下载逐行数据,然后基于Python 语言采用逐线计算方法建立了分子吸收光谱的理论模型。分子吸收光谱建模的建模流程如图2所示。

图2 分子吸收光谱建模流程图Fig.2 Flowchart of molecular absorption spectrum modeling
为了验证模型的准确性,将模型计算结果与“SpectraPlot.com”[15]分子气体集成光谱建模网站仿真结果进行对比。由于“SpectraPlot.com”网站利用HITEMP 数据库进行计算时,仅能计算纯物质气体或空气浴气体中辐射物质的二元混合物的光谱,故仿真计算的参数设置为:目标气体H2O,压强1 atm,浓度占比10%,模拟吸收光程15 cm,温度500 K,仿真波长范围7 174 ~ 7 192 cm-1。计算结果如图3所示。
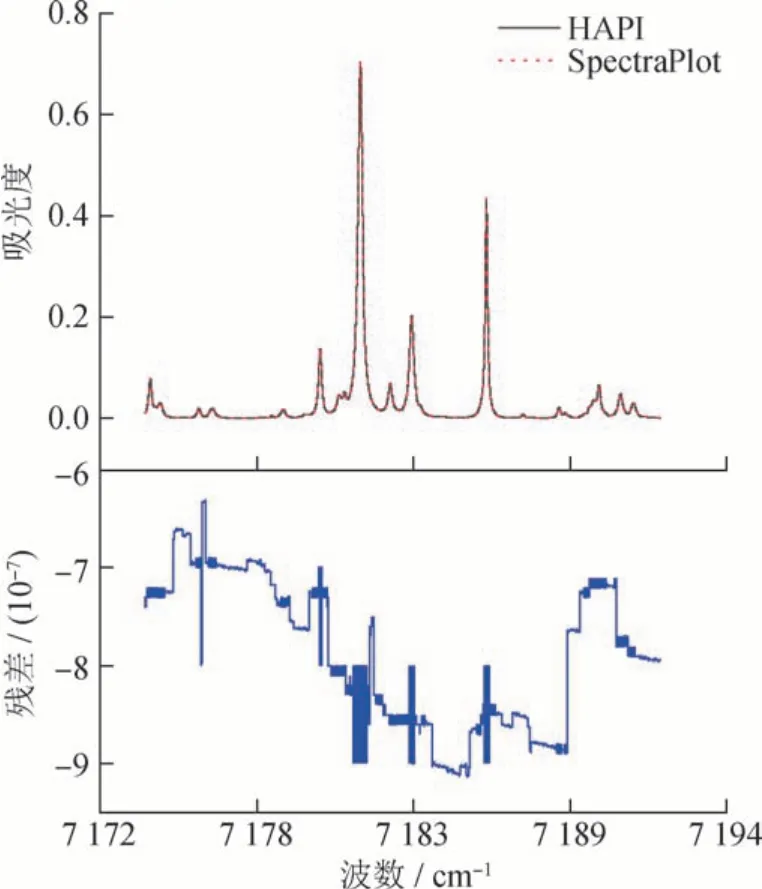
图3 HAPI光谱计算模型与SpectraPlot仿真结果对比Fig.3 Comparison between HAPI spectral calculation model and SpectraPlot simulation results
由图3 可知,HAPI光谱计算模型与SpectraPlot仿真结果基本一致,差值在10-7量级,满足精确计算误差10-5量级的要求。线型函数计算的精度和参与仿真计算的谱线范围是误差的主要来源。在确定了基于HITEMP 数据库的分子吸收光谱建模算法的准确性后,将对建立的模型进行优化处理。
2 分子吸收光谱模型的优化
2.1 线型函数的简化
一般地,Voigt 线型函数被当做模拟吸收光谱线形状的标准函数[16-17]。然而,随着实验得到的分子光谱质量的提高,由于谱线混合、速度依赖效应和Dicke窄化效应,Voigt线型函数已不能够准确的表示吸收谱线的形状。Tennyson[18]等人对此进行了探究,推荐采用pCqSDHC[14,19-20]作为高分辨力光谱分析的标准吸收光谱建模函数并将该函数命名为Hartmann-Tran 线型函数(HTP)[19]。Lisak[20]和Kim Year、Lim Jeong Sik[21]等人对HTP 理论模型的多谱拟合也证实了该线型函数在残差和拟合参数的精度方面提供了水分子光谱吸收线形状的准确描述。不考虑线混合效应的pCqSDHCP可以表示为
式中:ϕHT为Hartmann-Tran 线型函数,IpCqSDHC为pCqSDHCP 函数,HTP 共包含了7 个参数,Γ0和Δ0分别为碰撞展宽和位移,ΓD为多普勒展宽,Γ2和Δ2分别为速度加宽和位移,vVC为分子间碰撞引起的分子速度变化的频率,η为碰撞引起的分子速度变化与转动态变化的时间相关性。且大多数以前开发使用的线型函数都可以表示为pCqSDHCP函数的极限形式,可通过对相关参数的限制,利用HTP 线型函数求解程序求解。表2展示了几种常用线型函数与pCqSDHC模型的对应关系。

表2 几种常用线型函数与pCqSDHC模型的对应关系Tab.2 Correspondence between several common line shape functions and pCqSDHC model
由于pCqSDHCP 可以表示为CPF 函数的组合,针对CPF 函数的计算存在诸多简化模型,包括:Humlíče[22]于1983 年开发的基于CPF 计算程序、林洁丽提出的直和近似模型[23]、Mclean 等人[24]2012年开发的近似算法、Zaghloul等人分别在2012年和2017 年提出的两种简化模型Zaghloul-2012 和Zaghloul-2017[25-26]。图4 展示了直和模型与精确理论模型计算的线型函数的对比,其中d=(Γ0-ΓD)/(Γ0+ΓD)。

图4 d=-0.9、0.0、0.9时直和模型与理论模型对比Fig.4 Comparison between the Straight-Line model and the theoretical model for d = -0.9、0.0、0.9
图5(a)展示了5种简化模型与理论模型计算精度(使用残差均方根值衡量)对比,图5(b)为计算速度(以理论模型计算速度为单位)对比。从图5可以看出每种简化模型的计算精度和计算速度,Zaghloul-2017 模型计算速度为理论模型的25 倍,精度在10-7量级,满足高精度快速建模的要求。本文将Hartmann-Tran 线型函数作为光谱建模分析的标准模型,利用Python 实现基于Zaghloul-2017 模型的pCqSDHC 函数简化计算,将线型函数的计算速度提高了20倍。
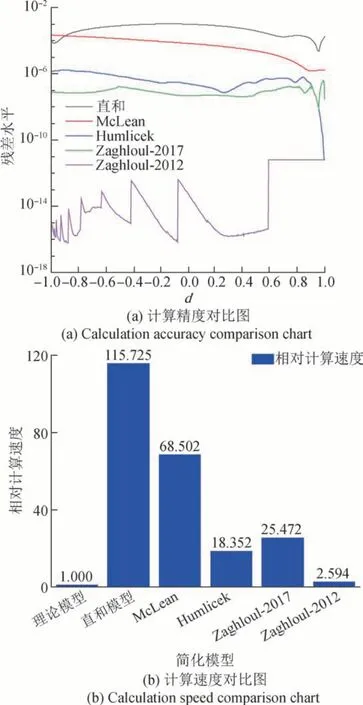
图5 五种简化模型与理论模型计算精度和计算速度对比图Fig.5 Comparison of calculation accuracy and calculation speed between five simplified models and theoretical models
2.2 线翼截止准则
线型函数在整个频率范围内是无限延伸的,而物质某一频率处的吸收系数是该物质所有吸收跃迁在该频率处的吸收系数的叠加,故理论上要得到物质在某一频率处的吸收系数,需要模拟计算数据库中该物质所有跃迁谱线的吸收系数,这对于吸收光谱模型的建立是一个挑战。如图4 所示,在远离跃迁中心频率处,归一化的线型函数值都迅速衰减,选择合适的线翼截止频率忽略谱线线翼的贡献可以保证吸收光谱模型的准确性和计算速度。
对于截断频率(Δvcutoff)的选择,常用的方法有固定波数截断、谱线半宽等倍数截断和绝对线强截断。其中,谱线半宽等倍数截断和绝对线强截断在窄线宽吸收光谱中应用广泛,对于宽光谱模拟常用固定波数截断。Goldenstein[15]等人通过研究不同温度和压力下H2O 和CO2在2.8 μm 和4.3 μm的吸收光谱,制定了由压力P确定截止频率的简单准则,具体为:当P≤10 atm时,Δvcutoff=200 cm-1;当10 <P≤100 atm时,Δvcutoff=20 cm-1/atm×P;其他情况下,Δvcutoff=2 000 cm-1。该准则被“SpectraPlot.com”原子分子综合光谱建模网站所采用,用于提供高精度的光谱建模。但针对HITEMP 数据库庞大的数据量,实施该准则时会耗费大量的计算时间。本文采用谱线半宽等倍数截断结合固定波数截断作为模型建立的线翼截止准则,下面利用建立的分子吸收光谱模型通过逐线计算确定合适的固定波数和半宽倍数。
如图6所示,模拟了不同线翼截止标准下水分子在7 184 ~ 7 189 cm-1的吸收光谱,如图例所示截止标准从1 cm-1到200 cm-1间隔取样,并以200 cm-1为标准计算其余截止频率的残差。

图6 不同线翼截止标准下水分子在7 184 ~ 7 189 cm-1的吸收光谱Fig.6 Absorption spectra of water molecule in the 7 184 ~ 7 189 cm-1 range under different line wing cutoff criteria
图7(a)展示了不同线翼截止标准下吸收光谱计算的误差,以200 cm-1为标准谱,虚线为10-5平均误差线,可知常压下线翼截止标准大于80 cm-1时模拟计算的吸收光谱具有较高的精度。图7(b)为不同截止标准下计算耗时,总体计算耗时随截止标准的增大而增加,具体计算中应结合实际需求选择合适的截止标准。为了兼顾模型计算的准确性和计算效率,本文建议常压下以80 cm-1作为线翼固定波数截断的截断标准。但是随着压强的增大,吸收谱线的展宽会迅速增大,此时按照常压下确定的固定波数截断会导致计算误差的增大。碰撞展宽参数Γ0可表示为压强的函数,如式(8)所示,其中Pref、Tref、Γ0ref分别为参考压强、温度和碰撞展宽参数,n为温度系数。故可以通过计算对应压力下的碰撞展宽参数建立谱线半宽等倍数截断准则。仿真模拟了300 ~ 3 000 K 和1 ~ 30 atm 下达到峰值吸光度0.01%的谱线展宽频率与谱线半宽倍数的关系,均在25 ~ 50 倍之间,结合Goldenstein[14]等人的准则,最终以50 倍的谱线半宽作为谱线半宽等倍数截断准则。

图7 不同线翼截止标准下水分子在7 184 ~ 7 189 cm-1的吸收光谱计算误差和计算时间对比图Fig.7 Comparison of the calculation error and calculation time of the absorption spectra of standard water molecules at 7 184 ~ 7 189 cm-1with different lineal wings
综上,确定线翼截止参数OmegaWingF 为固定波数截断设定值ω和50 倍碰撞展宽(Γ)中较大的值,其中Γ= max (Γ0,ΓD)。线翼截止准则的算法设计流程如图8所示。

图8 线翼截止准则的算法设计流程图Fig.8 Algorithmic design flowchart of the line wing cutoff criteria
2.3 谱线数据库的优化
HITEMP 数据库包含大量的谱线,仅H2O 就有超过1亿条跃迁谱线被记录,在本文关注的近红外6 500 ~ 8 000 cm-1波数范围内谱线数量约850 万条,而HITRAN 数据库在该波数范围内谱线数量仅2.4万余条。原因在于HITEMP 数据库包含了大量在高温下才表现出明显吸收的谱线,这些谱线数量多且分布密集,在常温下的线强度普遍小于10-25cm-1/(mol·cm-2),但都具有很高的低态能量值。图9展示了按照线强阈值筛选后计算的吸收光谱曲线和计算残差曲线,显然在低温时,对吸收谱线按照数据库提供的线强值进行筛选计算误差可忽略,但在高温时,由于谱线筛选剔除了高温敏感热线吸收的贡献,产生了不可忽略的计算误差,故不能按照简单的线强阈值判断该谱线是否应参与模型的建立。同时,图9展示了高温和低温范围内100 K 温差下的计算残差,无论在高温范围还是低温范围,100 K 的温差下不同线强阈值的计算模型残差处于同一个量级。
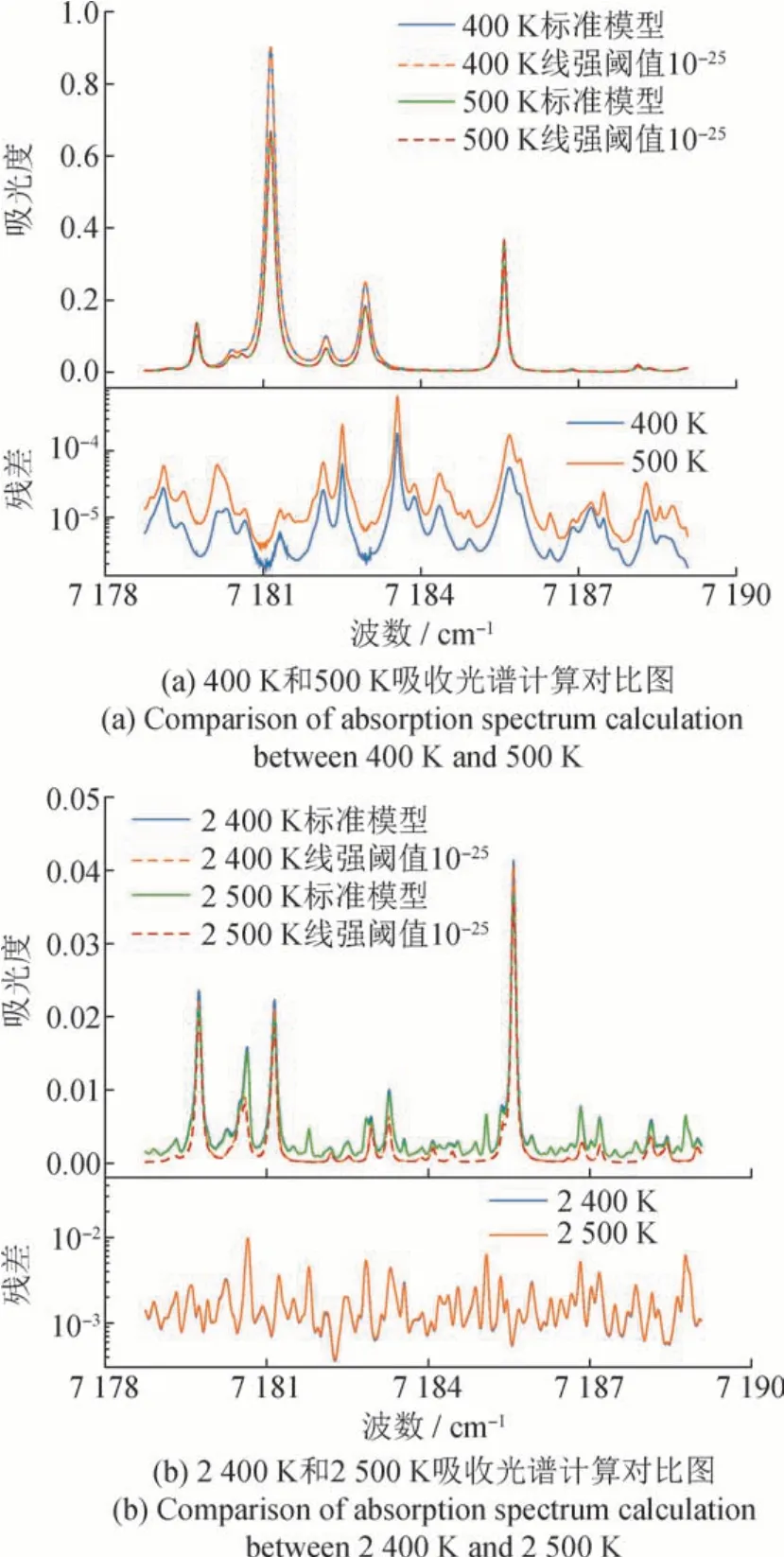
图9 线强阈值筛选前后不同温度下计算的吸收光谱曲线对比Fig.9 Comparison of absorption spectral curves calculated at different temperatures before and after line-intensity threshold screening
为了提高基于HITEMP 数据库的吸收光谱模型的计算效率,同时保证计算精度,本文计算了不同温度点(从300 K 到3 000 K,间隔为100 K)处的谱线线强度,并在对应温度点处筛选出谱线强度大于阈值线强度10-25cm-1/(mol·cm-2)的所有谱线,并对筛选出的谱线按照谱线跃迁频率进行合并处理,得到备选跃迁数据组,最后在HITEMP 数据库中提取出所有备选跃迁作为优化后的HITEMP 谱线数据库。图10 仿真计算了水分子在7 179 ~ 7 189 cm-1范围内不同温度点处基于原始数据库和优化数据库的吸收光谱,图中的细虚线为逐线计算中所有参与计算的跃迁谱线的吸光度曲线。结果表明基于优化数据库的吸收光谱计算结果具有良好的计算精度,低温时残差在10-7~ 10-5量级,高温时残差在10-5量级。优化前水分子在6 500 ~ 8 000 cm-1范围内有8 506 193 条谱线数据,优化后为347 964条,使用优化数据库的吸收光谱计算效率提升了25倍。
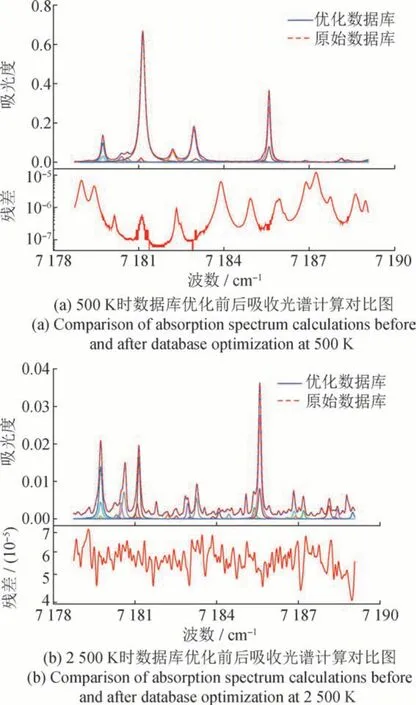
图10 使用优化前后HITEMP数据库计算的吸收光谱对比Fig.10 Comparison of absorption spectra calculated by HITEMP database before and after optimization
对所建立的模型进行优化的目的是在确保计算精度的前提下,尽可能地实现快速计算。减少参与逐线计算的谱线数量,是线翼截止准则和谱线数据库优化的目的,也是计算误差的主要来源。而线型函数的不同简化计算模型也将导致不同程度的误差。本文将与理论模型误差控制在10-5量级,完全满足实际应用中对理论吸收光谱的精确计算需求。
3 结论
针对吸收光谱测量技术中宽光谱测量对于吸收光谱高精度快速计算模型的依赖,本文基于HITEMP 数据库建立了分子吸收光谱逐线计算理论模型,并与“SpectraPlot.com”仿真结果比较,验证了逐线计算模型建立的准确性。通过比较5种针对CPF函数计算简化模型的计算精度和效率,确定了利用基于Zaghloul-2017 模型的pCqSDHC 函数实现线型函数的快速计算。仿真分析了不同截断波数的吸收光谱,并在10-5误差范围确定了基于固定波数截断结合谱线半宽等倍数截断的线翼截止准则。最后针对HITEMP 数据库大量的跃迁谱线,在不同温度点处根据线强阈值进行筛选,以水分子在6 500 ~ 8 000 cm-1范围为例,谱线数量从850 万条简化到34 万条,优化后吸收光谱计算误差在10-5量级,在满足计算精度的要求下将平均计算速度提升了25倍。
本文所建立的光谱计算模型基于逐线计算,对于HITEMP 数据库中的所有分子均适用,且从线型函数的快速计算、线翼截止准则以及谱线数据库的优化三个方面逐步对计算模型进行优化,所建立的优化准则也具有普适性,最终建立了基于HITEMP 数据库的分子吸收光谱快速高精度计算模型,为基于宽带超连续吸收光谱测量技术的发展提供理论计算模型基础。
尽管本文对基于HITEMP 数据库的分子吸收光谱模型进行了多方面的优化,但是HITEMP 数据库中数据量庞大,以水分子为例,优化后的光谱跃迁数量约为原始数量的4 %,其数据量仍然庞大。为了更好地满足实际应用中对于快速计算的需求,可以采取两方面的策略:一方面,依赖于更多线型函数快速计算模型的发展,以提升计算效率。另一方面,可以结合具体频率范围的使用情况,对跃迁谱线进行合并处理,以进一步减少谱线数量,提高计算速度。
