Investigation on the ballistic performance of the aluminum matrix composite armor with ceramic balls reinforcement under high velocity impact
2023-12-07AliAnsariTayeehAkariMasoomehRahimiPishijari
Ali Ansari ,Tayeeh Akari ,Masoomeh Rahimi Pishijari
a School of Mechanical Engineering, Iran University of Science and Technology, Tehran, Iran
b Faculty of Materials and Manufacturing Technologies, Malek Ashtar University of Technology, Tehran, Iran
c Islamic Azad University of Parand Branch, Tehran, Iran
Keywords: Ballistic Ceramic-reinforced Aluminum matrix Simulation Experiment
ABSTRACT In this research,the ballistic behavior of the ceramic-reinforced aluminum matrix composite plates is investigated to provide an optimal design for protecting against 7.62 mm bullet at the speed of 800 m/s experimentally and numerically.The target materials are Al5083 alloy as the metal matrix and alumina ceramic balls as the reinforcement.To simulate a 3D numerical model,ABAQUS FE code has been utilized.After validation the numerical model by experiments,the effect of ceramic ball weight percentage include 15%,30% and 45% and the target thickness 20,25 and 30 mm is considered on the ballistic results like the kinetic energy,residual velocity and depth of penetration.Finally,it was found that the specimen with 25 mm thickness and 30% alumina is optimum based on existing ballistic protection criteria.
1.Introduction
After iron steels,aluminum alloys (AAs) is the second most commonly used metal due to its good mechanical properties.These materials have an important place among engineering materials due to their low density,good thermal and electrical conductivity,corrosion resistance,and high strength-to-weight ratio [1-4].But the main problem of aluminum alloys is their poor wear resistance and stability at high temperatures.To solve these problems,researchers have reinforced these materials with ceramic particles and made metal matrix composites(MMCs)[5-7].AA-based MMCs reinforced with ceramic particles show higher mechanical properties compared to non-reinforced AAs.Studies have shown that MMCs are attractive engineering materials in many applications due to their superior mechanical properties and various advantages in applications such as nuclear power plants,armor,automotive parts,marine parts,and aerospace parts [8,9].
McWilliams et al.[10]investigated the effect of fabric architecture on the ballistic behavior of metal matrix composites.In this study,the ballistic limit,VBL50 of four composites with different fabric architecture was measured and the mechanism of damage was determined.They validated the experimental results using ABAQUS/Explicit.Finally,it was found that fabric architecture has significant effect on ballistic behavior and through thickness shear strength of the MMC.Pawar et al.[11]explored and compared the ballistic performance of alumina and aluminum nitride ceramics in bi-layer ceramic/aluminum armor against 7.62 armor piercing bullets.The material models which used in this study are Johnson-Cook model for metal materials and Johnson-Holmquist model for ceramic materials.The samples simulated and made in the laboratory were alumina/aluminum 5083 and aluminum nitride/aluminum 5083 composites.The results showed that aluminum nitride ceramics have better performance than alumina.Venkatsan et al.[12]evaluated and compared the ballistic performance of bi-layer alumina/aluminum and silicon carbide/aluminum armor against impact of ogive and blunt projectiles numerically.The results showed that the ballistic performance of silicon carbide/aluminum armor is better than alumina/aluminum armor.It was also found that the shape of the projectile nose has a significant effect on its residual velocity.Lee et al.[13]investigated the metal matrix composite used in armor systems.The length to diameter ratio of the projectile used in this research is 10.6.Also,two types of silicon carbide and boron carbide reinforcements have been used in making composite samples.To calculate the mechanical properties of the samples,the high-speed Hopkinson bar test was used.Based on the numerical and experimental results,they evaluated the depth of penetration in the samples and their comparison with semi-infinite steel samples.Finally,they investigated the performance of metal matrix composites used in armor systems and showed that the armor system performed better when the ceramic was placed in the front layers.
Venkatsan et al.[14]considered the ballistic performance of bilayer armor with different backing against ogive projectiles numerically and experimentally.In this research,bi-layer samples of ceramic/aluminum were made.Alumina 95% and 1100,2024,6061 and 7075 aluminum alloys were used to make these samples.The projectile was 4340 steel and its speed was 493,820 and 1200 m/s.Their results showed that the ballistic resistance of the samples is different for various aluminum alloys.Also it was found that the best ballistic resistance is achieved when 7075 aluminum is used as a backing in bi-layer armor.Arslan et al.[15]examined the ballistic performance of ceramic/metal armored structures.The materials used in the armored structures were boron carbide(B4C),6061 aluminum,4340 steel and epoxy resin adhesive.They showed that bi-layer armored structure with 4340 steel backing plate has better ballistic performance in terms of speed than 6061 aluminum backing plate in the same thickness and areal density.When 4340 steel is used as the backing plate,the damage level including crack size and crack propagation on the front surface of the ceramic is higher than the 6061 aluminum backing plate due to the higher stiffness of steel.Seifert et al.[16]evaluated the ballistic performance of ceramic/metal tiles in the gap between the tiles and the projectile impact conditions.In this study,a projectile with a 7.62 tungsten carbide core was used.Their results showed that when the projectile hits the edge of the tile,the residual velocity is higher than the projectile which hits the middle of the gap.In addition,by decreasing adhesive stiffness and increasing gap widths,the ballistic resistance is significantly reduced.
Tian et al.[17]studied four hybrid samples numerically and experimentally to determine the effect of ceramic constraint on penetration resistance.The results showed that the penetration resistance significantly depends on the size of the ceramic,the boundary constraint and the mode of connection between the components.Also,all four hybrid samples performed much better than monolithic TC4 plate with the same areal density.An et al.[18]investigated the influence of metallic materials on the penetration resistance of ceramic-metal specimens against tungsten rod projectiles.In the middle of these hybrid structures,cores of titanium alloy TC4(Ti6Al4V),AISI 4340 steel and 7075 aluminum alloy were placed.It was found that the hybrid structure of Ti6Al4V at the same areal density has the best penetration resistance compared to other structures.Zhao et al.[19]conducted an experimental and numerical study on the ballistic performance of three bi-layer alumina/aluminum armored plates with different structures at the striking surfaces.The striking surfaces of these plates were monolithic alumina,mosaic alumina,and mosaic alumina enhanced by aluminum honeycomb,respectively.The results showed that for enhanced mosaic armored plate,the honeycomb lattice acts as a cellular skeleton to limit the ceramic tiles and fragments,which leads to increase the ballistic resistance.Also,the enhanced honeycomb mosaic plate has better multi-impact ballistic resistance compared to other plates.
Rathod et al.[20]investigated the ballistic performance of ceramic plates with aluminum backing against cylindrical tungsten projectiles numerically.The ceramics used were alumina and boron carbide.The important parameters were considered in this study are areal density,depth of penetration and ballistic limit.The tungsten projectile hit these plates at a speed of 1550 m/s.Finally,it was found that in the same conditions,boron carbide performed better than alumina in all parameters.Sun et al.[21]explored the effect of the thickness of cover plate on the ballistic performance in ceramic armor with metal backing.The ceramic used was silicon carbide (SiC) and the cover plate material was 4340 steel.In this research,a tungsten rod projectile with a diameter of 2 mm was used.The thickness of the cover plates varied between 3 and 8 mm.The numerical simulation results showed that the best ballistic performance of the armor is when the thickness of the cover plate is 3-5 mm.Luo et al.[22]investigated the effect of metal cover plates on the ballistic performance of silicon carbide.In this research,silicon carbide plates were coated with aluminum alloy,mild steel and copper alloy.These plates were impact by a tungsten projectile of 16 mm diameter and 40 mm length at a speed of 1250 m/s.The results showed that the cover plate can effectively reduce the target damage.Gour et al.[23]studied the numerical simulation of performance of silicon carbide plates and 4340 steel backing and titanium alloy and graphite cover plate against normal and oblique impacts of a long rod tungsten projectile.The results showed that the cover plate removes impact shock from ceramic and amount of stress on the front surface of the ceramic decreases.Zhai et al.[24]evaluated the impact resistance of steel/ceramic/concrete composite plates.In this work,normal concrete,ultrahigh performance concrete (UHPC) and silicon carbide ceramic were used to make samples.The numerical results of LS-DYNA were compared with the experimental results and validated.Finally,SiC ceramic and steel/ceramic/UHPC composite structure were confirmed as a promising protective material and the target configuration with the best performance.
Sharma et al.[25]examined the performance of Functionally Graded Materials (FGM).The reinforcement of FGM material was Boron carbide and its matrix was Al-Zn-Mg-Cu.The samples with different composition were made by hot pressure assisted sintering.After analytical analysis,some experimental tests were performed and the optimal sample for protection against projectile 7.62 mm × 39 mm with a speed of 700 m/s was presented.
In addition to the researches which concern the ceramics as the armor plates,a few studies are considered the ceramic particles as reinforcement in composite armors.The Liu et al.[26]investigated the impact of high velocity (500-850 m/s) rigid projectile against ultra-high performance concrete (UHPC) target protected by the ceramic balls numerically.They studied the perforation process and obtained the ballistic limit of ceramic balls protected UHPC plates.Also they explored the effect of diameter,material type of ceramic balls and their arrangement and the impact position on target.Celikbas et al.[27]studied the effect of ceramic sphere radius and bullet impact location on the ballistic performance of the alumina ceramic tile numerically.The parameter studied in this research was the specific kinetic energy absorption (SKEA) of alumina.LSDYNA software was used for numerical analysis.Finally,it was found that the highest amount of SKEA occurs when a bullet hits between the spheres and the lowest amount of SKEA occurs when the bullet hits the top of the ceramic sphere.Pol et al.[28]fabricated AA7005 alloy composite with TiB2and B4C ceramic reinforcement particles and evaluated the ballistic behavior of these armors.Surface composites with different weight fractions of TiB2and B4C particles were processed by friction stir processing.Microhardness and depth of penetration tests were carried out to evaluate the ballistic properties of the surface composites.There results showed that the depth of penetration was 20-26 mm in composite armor as compared to 37 mm in the base alloy.
Santos et al.[29]produced and evaluated the ballistic performance of niobo-phosphate glass-doped alumina composites.The niobo-phosphate glass (30% Nb2O5-30% P2O5-20% CaO -20% CaF2,by mol) were added to the alumina in six different weight percentages.The composite with the highest densification was used for the ballistic tests.In this work,the sintered samples were enveloped on two 1020 steel plates for the residual velocity test.Finally they found that the niobo-phosphate glass addition of 4 wt% worked properly as sintering aid for alumina,enhancing its properties and performance.
In the present study,a ceramic-reinforced aluminum matrix composite armor was proposed.To achieve a suitable design of the composite armor,some important parameters like thickness and the percentage of the ceramic particles were investigated numerically.ABAQUS software was used to simulate the penetration process against the 7.62 mm×39 mm FMJ(57-N-231)projectile.To verify the simulation results some experimental ballistic tests were performed according to GOST armor standard.
2.Experiments
The prepared specimens and ballistic tests are described in the following.
2.1. Materials
In this research,composite armor is fabricated from alumina 99.5% balls as the reinforcements and aluminum Al5083 ingots as the matrix.Alumina balls are supplied from Shenyang Vhandy Technology Company.
2.2. Specimen preparation
In the present study,the test samples of composite armor is fabricated from aluminum Al5083 and 30 wt percentage of alumina reinforcements.Alumina balls are mixed in the aluminum matrix by the squeeze casting method.The test sample is illustrated in Fig.1.

Fig.1.Test sample.
2.3. Ballistic test
After fixing the target by a clamped support according to Fig.2,a 7.62 mm×39 mm FMJ bullet is launched from the AK-47 rifle at the distance of 5 m according to GOST armor standard (Russia).The projectile mass is 8 gr approximately and its velocity is estimated between 750 to 800 m/s.Three specimens have been made and tested to insure the test results.Fig.3 shows the 7.62 mm×39 mm FMJ projectile components and average profile for core,filler and the jacket recorded by profilometer [30]and Fig.4 presents the ballistic test schematically.

Fig.2.Clamped support for the ballistic test.
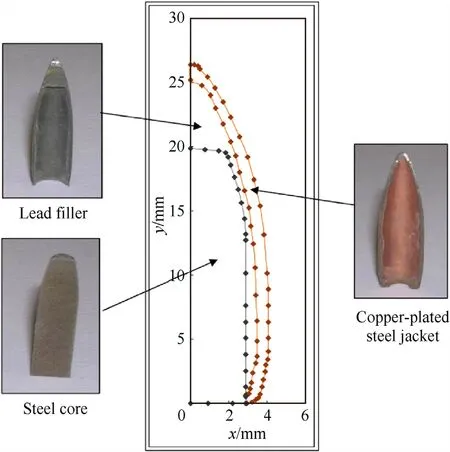
Fig.3.Average profile of 7.62 mm × 39 mm FMJ bullet composition [30].

Fig.4.Schematic of the ballistic test.
3.Numerical simulation
3.1. Numerical model
In this research the optimal design of the metal matrix composite armor again 7.62 mm×39 mm projectile is investigated.The important parameters which consider in the current study are presented in Table 1 briefly.

Table 1 Problem variables.
ABAQUS FE code is used to construct a numerical model for studying the ballistic behavior of a metal matrix composite armor embedded with the ceramic particles.The projectile and the region of the target that undergo large plastic deformations are modeled using 3D finite element simulation.Because the brass jacket of the projectile has no effect on the penetration [31,32],the projectile geometry is simplified with the radius 4 mm and length 28 mm to achieve 8 gr mass as shown in Fig.5.
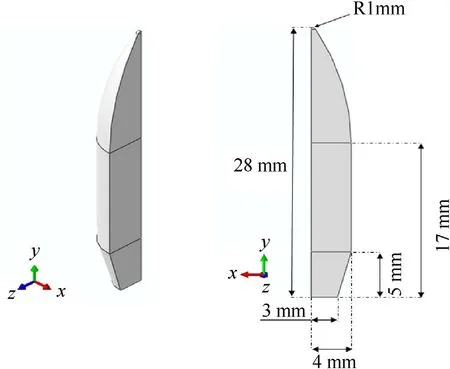
Fig.5.Geometry of the projectile.

Fig.6.Front plate of the target.
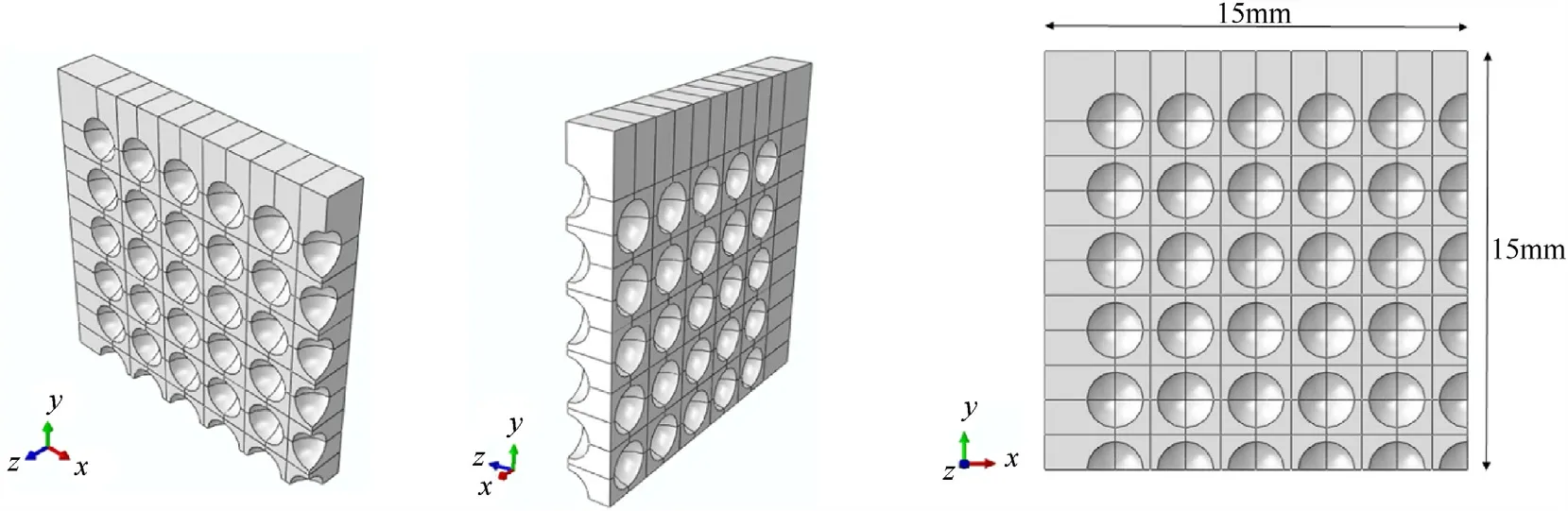
Fig.7.Middle plate of the target.
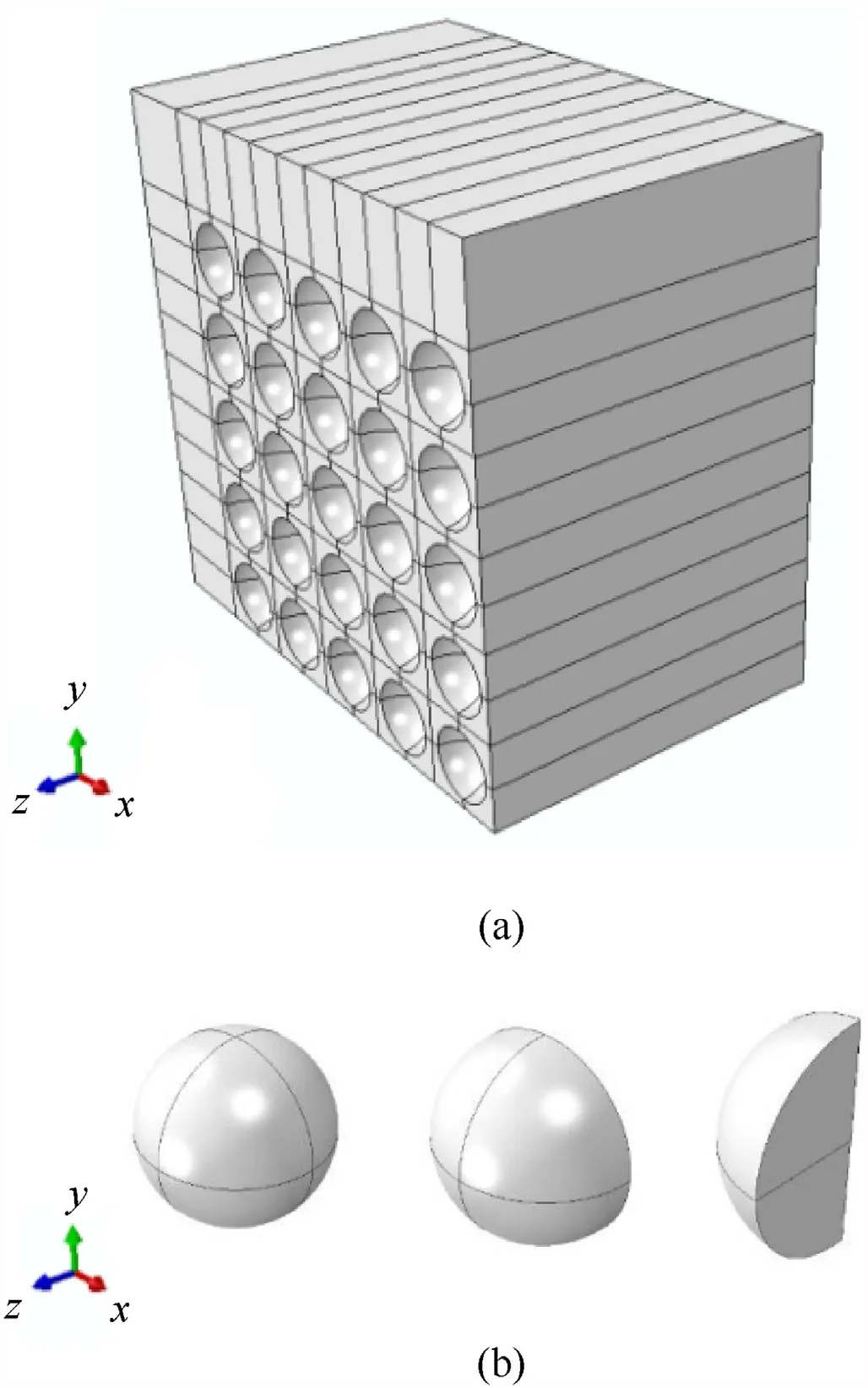
Fig.8.(a) Back plate of the target;(b) Ceramic balls.
By axisymmetric nature of the problem,one-fourth of the model is used to reduce the computing costs.The aluminum matrix is modeled by several plates which called front,middle and back plates.The length and width of all layers of target is 30 mm.For locating the ceramic balls,hemispherical cavities with the radius 1 mm and distance 0.4 mm are considered.Figs.6-8 illustrate FE model of the front plate,middle plate and the back plate of the target and the ceramic balls respectively.The front plate thickness is 1.2 mm and the middle plate thickness is 2 mm.Thickness of the back plate is varied by the weight percentage of the ceramic particles and the total thickness of the target in each simulation.
The symmetry planes are applied to displacement constraint in thexandydirection according to Fig.9.In the target lateral surfaces,all degrees of freedom are closed to consider the clamped supports.Also the constraint between the aluminum plates and the aluminum plates and the ceramic balls are considered to be tie.
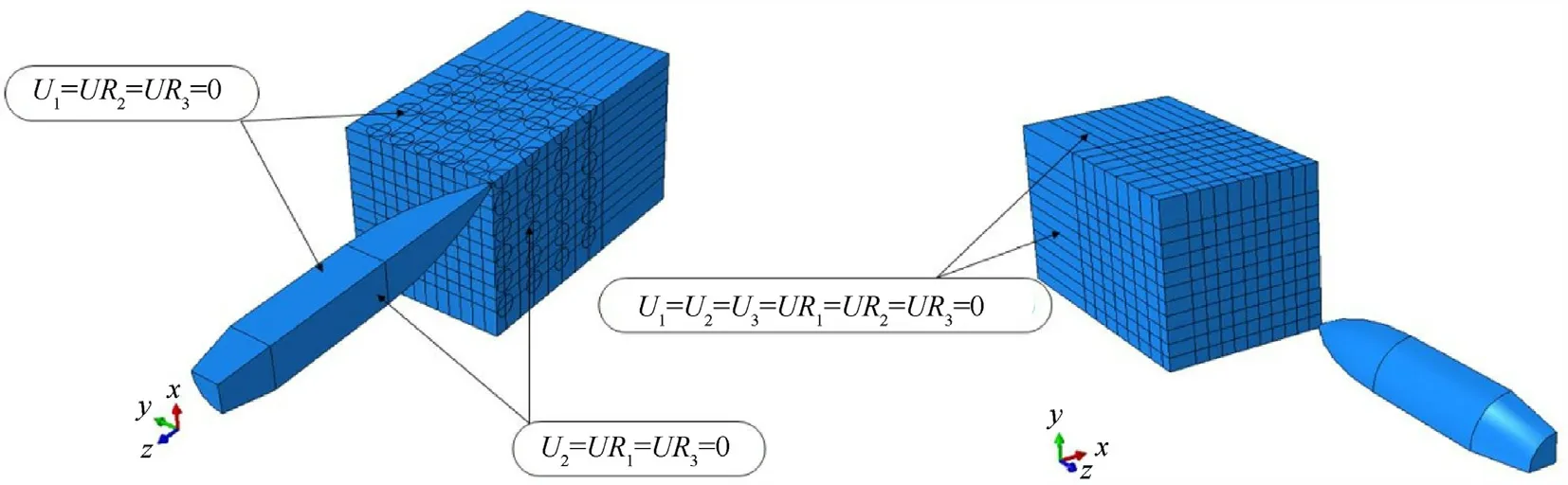
Fig.9.Boundary conditions.
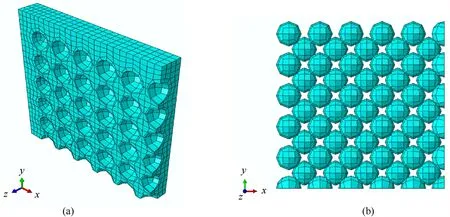
Fig.10.3D solid element meshes used in the simulation: (a) Aluminum plate;(b) Ceramic balls.

Fig.11.The numerical model.
In this study,to simulate the target and projectile,8-node linear brick,reduced integration,hourglass control (C3D8R) elements have been utilized.Figs.10 and 11 illustrate the FE model meshes.
The convergence of the simulation results is checked and controlled by choosing the suitable contact between the target and projectile and matching the mesh size.Mesh study shows that the optimum mesh size of the projectile and the target is 0.35 mm and the total number of elements are 53877.
3.2. Mechanical behavior of materials
3.2.1.Metal materials model
The Johnson-cook model is the suitable constitutive equation for ductile materials like aluminum and steel in large strain rate problems [33].Flow stress σ in this model is expressed as
In the above equations,A,B,C,nand m are Johnson-cook material behavior coefficient and ε is the plastic strain,˙ε the equivalent strain rate,reference strain rate,Tcurrent temperature,T0room temperature andTmis the melting temperature.
The damage model of Johnson-cook is as follow:
where D is the damage parameter,Δεpis the variation of the plastic strain andis the plastic strain at failure given by
where σ*is the average of three principle stresses to Von-Mises equivalent stress ratio andis equal to
A detailed information on this model can be found in Ref.[33].Table 2 is described the constant parameters of Johnson-cook model for 5083 aluminum and hardened steel used as metal matrix and projectile respectively.

Table 2 Material parameters of aluminum alloy matrix and steel projectile.
3.2.2.Ceramic material model
Johnson-Holmquist (JH-2) constitutive modeling is well suited to model the brittle failure of ceramic materials.This model is based on a polynomial equation which evaluate the current state of pressure as a function of a volumetric change [35].This model explain the strength of materials based on Von-Mises stress as below.
where σ*,andare the equivalent stress,intact and fractured ceramic strengths respectively which describe as follow andDis the damage parameter.
In the above equations,σ is Von-Mises stress,σHELis the equivalent stress at the Hugoniot elastic limit,A,B,Care the Johnson-Holmquist parameters,P*is the normalized pressure andT* is the tensile strength that described as below.Alsoandare maximum intact and fractured ceramic strengths.
wherePis the pressure,PHELis the pressure at the Hugoniot elastic limit andTis the maximum tensile strength [36].
Because the ABAQUS software material library doesn't have Johnson-Holmquist(JH-2)constitutive equation,a similar model to JH-2 which is a combined model include Drucker-prager formulation and Mie-Gruneisen EOS is proposed to define the ceramic materials.
The flow stress in Drucker-Prager model is as follows:
and the JH-2 strength is presented as
By comparing Eqs.(12) and (13),
The compressive yield stress σccould be obtained from Eq.(17).
To model the damage mechanism of ceramics,the damage model of Johnson-Holmquist is modified and presented as follow:
whereD1andD2are the material constants.The initial hydrostatic pressurePis related to density according to the polynomial EOS as below.
whereK1,K2,andK3are constants(K1is the bulk modulus),ρ0is the initial density and ρ is the current density.
Damage initiation criteria in ABAQUS needs to determine the plastic strain at failureas the equation of stress triaxiality.Stress triaxiality diagram is defined parallel to intact strength in JH-2 model as follow:
By replacing Eqs(24)in Eq.(23),the damage initiation criteria is obtained.Finally,the relation between the plastic strain at failure of Drucker-Prager model and JH-2 model is defined as follow:

Table 3 Mechanical properties of Alumina [38].

Table 4 Stress triaxiality and Plastic strain at failure for Drucker-Prager damage model of ceramic.
3.2.3.Equation of state(EOS)
To specify the plastic behavior of material at high pressures,the relationship between the hydrostatic pressure,the local density and local specific energy has been used.This relation is famed as the equation of state(EOS).The useful EOS for solid materials under shock wave is Mie-Gruneisen EOS.This equation is presented as follow:
wherePis hydrostatic pressure,c0is elastic wave speed,Eis internal energy,S1,S2,S3are slop inUsversusUpdiagram and γ0,μ are the Gruneisen coefficient,ρ0is the initial density and ρ is the current density [35].Table 5 presents Mie-Gruneisen EOS parameters for 5083 aluminum,hardened steel and Alumina.

Table 5 Parameters of Mie-Gruneisen EOS for 5083 aluminum,hardened steel and Alumina.
4.Results and discussion
4.1. Validation of FE model
To verify the validity of FE model,the damage of armor plates were compared through experiment and simulation.Three specimens have been made and tested to insure about the experimental results.Fig.12 shows the damage of the composite armors with 30% ceramic balls.Fig.13 presents the penetration process of 25 mm thick metal matrix composite armor with 30% ceramic balls.

Fig.12.Damage of metal matrix composite armor: (a) Sample 1;(b) Sample 2;(c)Sample 3.
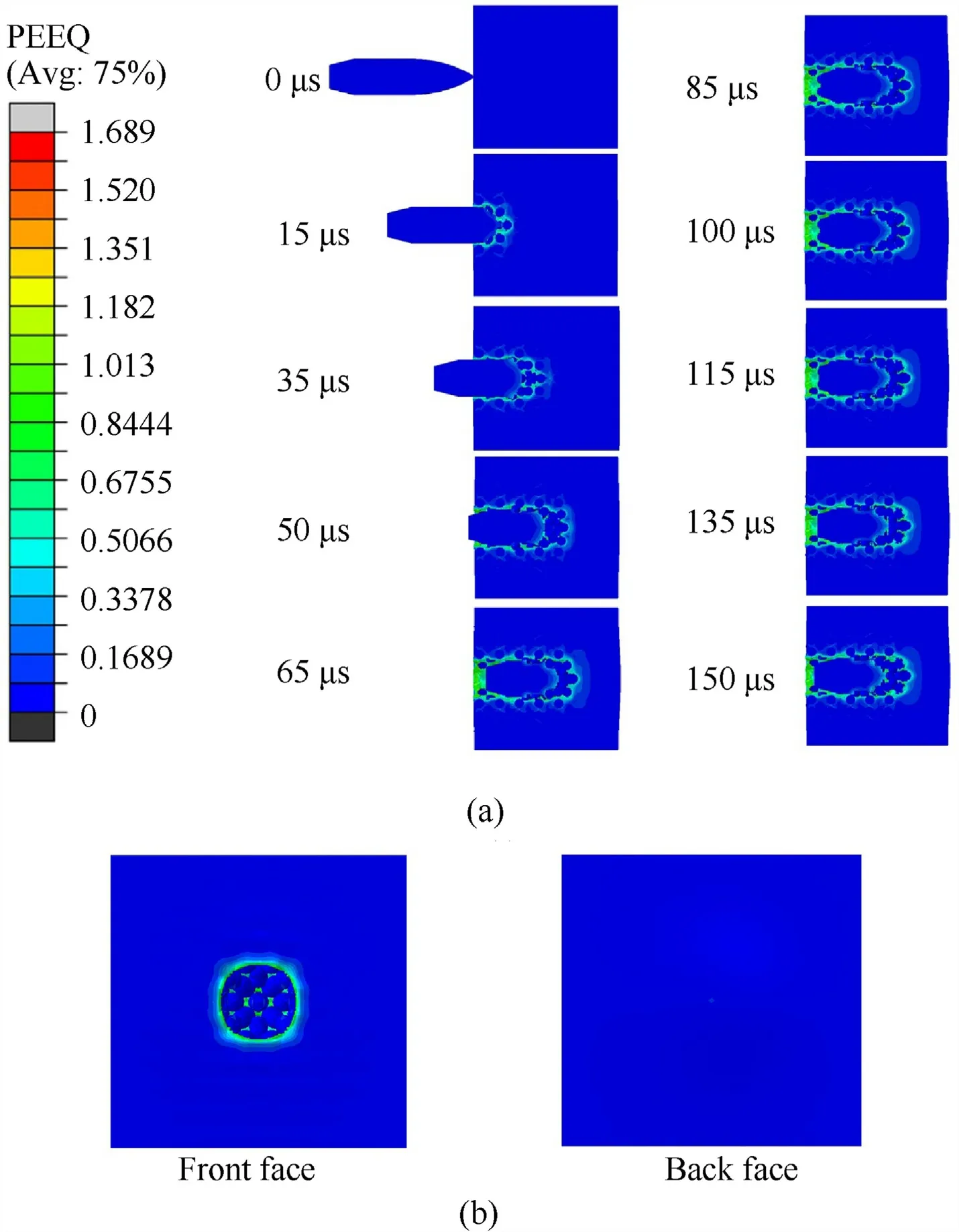
Fig.15.Penetration process of 30 mm thick metal matrix composite armor with 30% embedded ceramic balls: (a) Equivalent plastic strain contour;(b) Front and back faces.

Fig.16.Penetration process of 30 mm thick metal matrix composite armor with 15% embedded ceramic balls: (a) Equivalent plastic strain contour;(b) Front and back faces.

Fig.18.Penetration process of 25 mm thick metal matrix composite armor with 30% embedded ceramic balls: (a) Equivalent plastic strain contour;(b) Front and back faces.
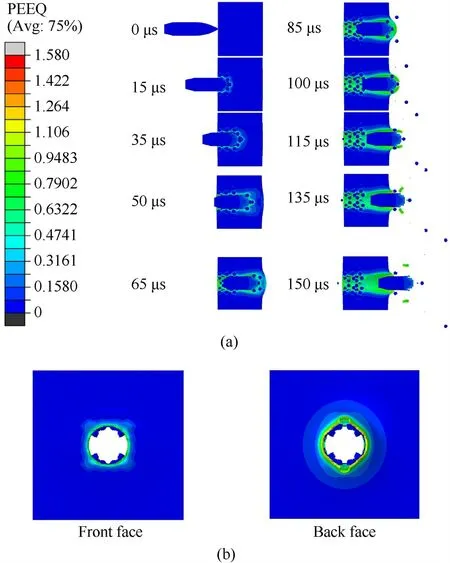
Fig.19.Penetration process of 25 mm thick metal matrix composite armor with 15% embedded ceramic balls: (a) Equivalent plastic strain contour;(b) Front and back faces.

Fig.20.Penetration process of 20 mm thick metal matrix composite armor with 45% embedded ceramic balls: (a) Equivalent plastic strain contour;(b) Front and back faces.
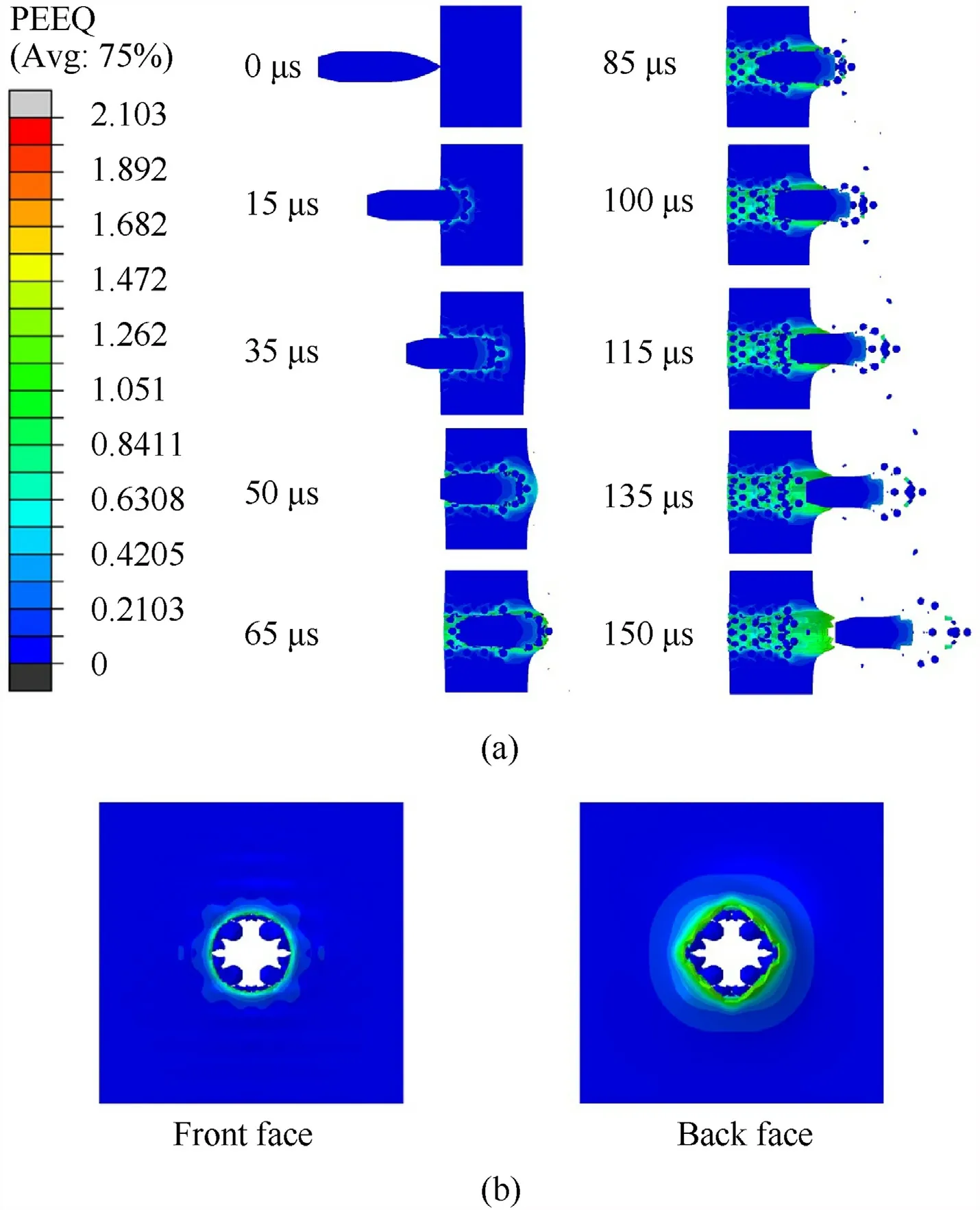
Fig.21.Penetration process of 20 mm thick metal matrix composite armor with 30% embedded ceramic balls: (a) Equivalent plastic strain contour;(b) Front and back faces.

Fig.22.Penetration process of 20 mm thick metal matrix composite armor with 15% embedded ceramic balls: (a) Equivalent plastic strain contour;(b) Front and back faces.
In Table 6,the numerical and experimental results of the penetration process of the composite armor is presented.The results show that the numerical modeling can simulate the ballistic behavior of metal matrix composite armor with ceramic ball reinforcements in sufficient accuracy.The discrepancy between the numerical and the experimental results could be due to the material properties approximation,meshing complexity of the solid geometry and the obliquity from the normal impact in experimental test.

Table 6 Penetration depth comparison in experiment and simulation.
4.2. Composite armor performance
The best criterion to evaluate the performance of armors is their areal density.Areal density is the weight per unit area of the armor required to provide protection against a particular treat which calculate as follow:
whereAdis areal density in kg/m2,Mais the armor mass andAais protected surface by armor.The mass effectiveness(Em)of different armor material is thus the ratio of areal density of RHA1Rolled Homogeneous Armor (RHA).to that of the respective armor material [40].
In Table 7,areal density and mass effectiveness of current experimental samples are presented.As can be seen,the mass effectiveness of all specimens are between 1.63 and 1.68.It should finally be mentioned that the current armor is about 40% lighter than RHA.
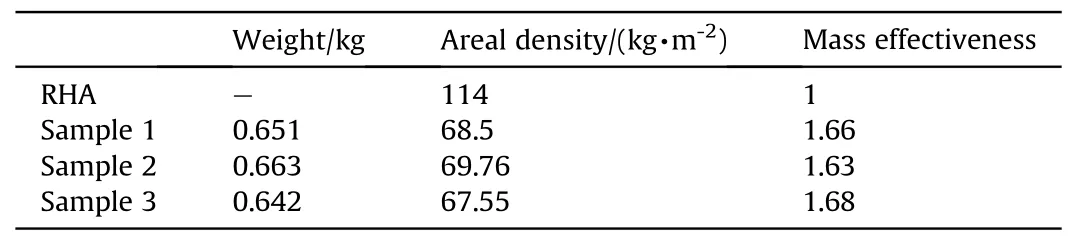
Table 7 Performance of the metal matrix composite armor with embedded ceramic balls.
4.3. Numerical results
In the following sections,the numerical results include penetration depth and equivalent plastic strain contour of the penetration process is presented.The equivalent plastic strain in a material (PEEQ) is a scalar variable that is used to represent the material's inelastic deformation.If this variable is greater than zero,the material has yielded [41].
4.3.1.Effect of ceramic balls weight percentage on the penetration process of 30 mm thick armor
In the current work,the ceramic balls weight percentage is varied from 15%,30% and 45% in metal matrix composite armor.Figs.14-16 show the penetration process and damage distribution on the front face and the back face of the 30 mm thick composite armor with 45%,30% and 15% ceramic ball reinforcements respectively.
According to these pictures,the perforation process is not completed and the composite armor could stop the projectile in all samples and these impacts don't have any effect on the back face of the plates.It's due to the mechanical properties of Al5083 and the ceramic particles like there toughness and high ballistic strength.
4.3.2.Effect of ceramic balls weight percentage on the penetration process of 25 mm thick armor
Figs.17-19 show the penetration process and damage distribution on the front face and the back face of the 25 mm thick composite armor with 45%,30% and 15% ceramic ball reinforcements respectively.
As can be seen in these figures,in the samples with 45% and 30% ceramic balls,the composite armor could stopped the projectile but the back face is affected by the impact.In the sample with 15% ceramic balls,the armor plate could not catch the projectile and the perforation process is completed.
4.3.3.Effect of ceramic balls weight percentage on the penetration process of 20 mm thick armor
Figs.20-22 show the penetration process and damage distribution on the front face and the back face of the 20 mm thick composite armor with 45%,30% and 15% ceramic ball reinforcements respectively.
According to these figures,the projectile pass through all the samples and the penetration process is complete.
4.3.4.Ceramic balls weight percentage influence on the ballistic results
In this section,the influence of the ceramic reinforcements on the ballistic results of the penetration process of the composite armor is described.The ballistic results include residual velocity,kinetic energy and depth of penetration.
Fig.23 illustrates the variation in velocity and kinetic energy of the projectile impacted on the 20 mm thick armor plate.As shown in these diagrams,increasing the weight percentage of ceramic balls cause to decrease the velocity and kinetic energy of the projectile and the projectile perforated the composite armor completely.
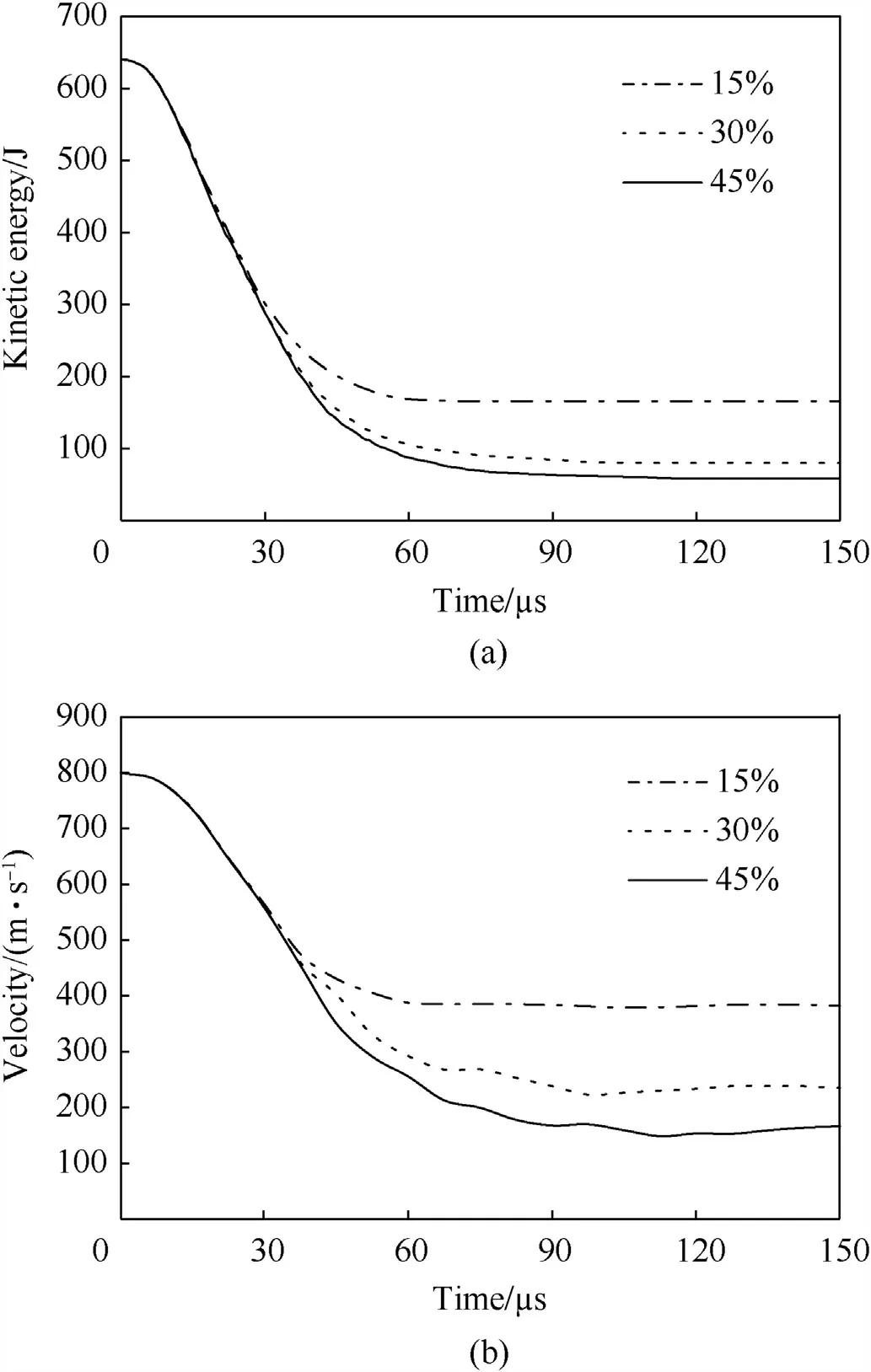
Fig.23.(a) Kinetic energy and (b) velocity variation of the projectile impacted on the 20 mm thick armor plate.
Fig.24 displays the velocity and kinetic energy change of the projectile impacted on the 25 mm thick armor plate.As expected,increasing the weight percentage of the ceramic balls cause to decrease the velocity and kinetic energy of the projectile.But in the samples with 30% and 45% ceramic balls,the velocity is reduced to zero and the perforation process is not complete.

Fig.24.(a) Kinetic energy and (b) velocity variation of the projectile impacted on the 25 mm thick armor plate.
In Fig.25 the velocity and kinetic energy variation of the projectile impacted on the 30 mm thick armor plate is shown.As can be seen,increasing the armor thickness cause to increase the performance of the armor to catch the projectile without depending on the ceramic balls weight percentage.

Fig.25.(a) Kinetic energy and (b) velocity variation of the projectile impacted on the 30 mm thick armor plate.
Fig.26 shows the ceramic ball weight percentage and armor thickness effect on the penetration depth.According to this figure,in 20 mm thick composite armor plate,the perforation process is complete without considering the ceramic ball percentage.In the samples with 25 and 30 mm thickness,enhance the ceramic ball percentage caused to reduce the penetration depth obviously.It should be noted that in the samples with 25 and 30 mm thick and 30% and 45% ceramic balls,the penetration depth is decreased due to the effect of semi-infinite target.
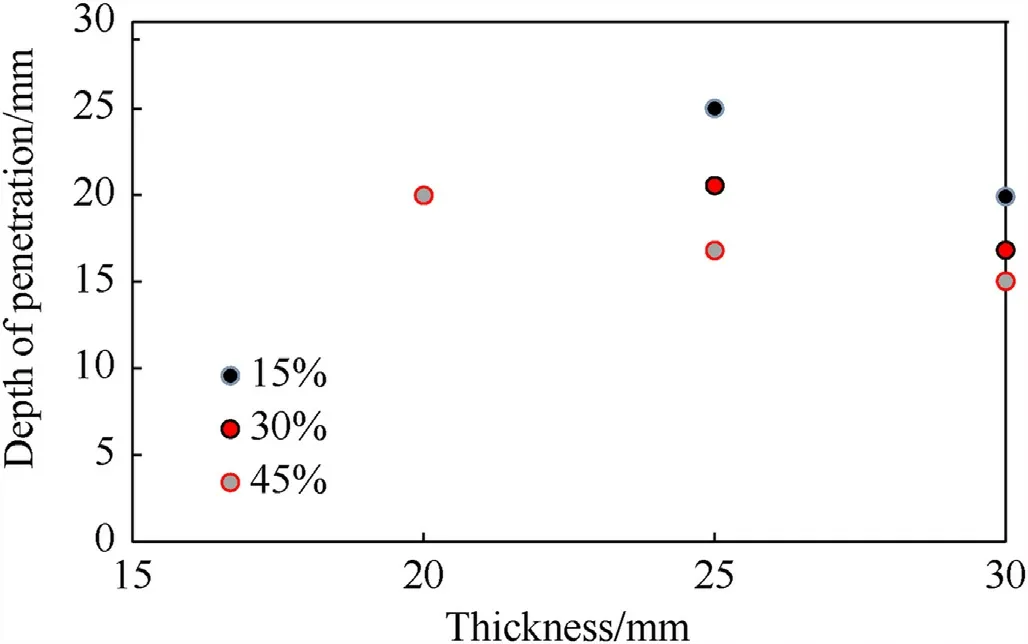
Fig.26.Penetration depth versus armor thickness in different ceramic ball weight percentage.
Fig.27 indicates the residual velocity of the projectile according to the armor thickness in different ceramic ball percentage.As shown in this Figure,the samples with 25 mm and 30 mm thick targets in all amount of ceramic balls could stop the projectile except the one with 15% ceramic balls and 25 mm thickness.In the models with 20 mm thickness,by increasing the amount of the ceramic balls,the residual velocity of the projectile is decreased.

Fig.27.Residual velocity versus armor thickness in different ceramic ball weight percentage.
5.Conclusions
In this paper,the ballistic behavior of aluminum matrix composite armor with ceramic particle reinforcements is investigated by experiments and simulation and the optimal design based on the ballistic protection criteria is determined.The main results of this study are summarized as follows.
1 Some vertical impact tests of 7.62 mm×39 mm projectile at the velocity 800 m/s were performed to investigate the damage mechanism of the composite armor experimentally and verify the numerical model.
2 The armor with 25 mm thick and 30% ceramic balls is the optimal design for composite armor.The ballistic performance of the optimum armor is calculated which the areal density is 68.6 kg/m2and the mass effectiveness is 1.65 in average.
3 In all samples by increasing the ceramic ball weight percentage,the ballistic results are improved like reduce in residual velocity and penetration depth.
4 In the samples that the perforation process is not complete,by increasing the armor thickness,the penetration depth is decreased because of the semi-infinite target effects.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
杂志排行
Defence Technology的其它文章
- High-Velocity Projectile Impact Behaviour of Friction Stir Welded AA7075 Thick Plates
- Dynamic analysis of buried pipeline with and without barrier system subjected to underground detonation
- Influence of liquid bridge force on physical stability during fuel storage and transportation
- Adaptive fuze-warhead coordination method based on BP artificial neural network
- Cooperative multi-target hunting by unmanned surface vehicles based on multi-agent reinforcement learning
- AI-based small arms firing skill evaluation system in the military domain
