Cooperative multi-target hunting by unmanned surface vehicles based on multi-agent reinforcement learning

Jiwei Xi ,Ysong Luo ,* ,Zhikun Liu ,Ylun Zhng ,Horn Shi ,Zhong Liu

a College of Weaponry Engineering, Naval University of Engineering, Wuhan, 430033, China

b Institute of Vibration and Noise, Naval University of Engineering, Wuhan, 430033, China

Keywords: Unmanned surface vehicles Multi-agent deep reinforcement learning Cooperative hunting Feature embedding Proximal policy optimization

ABSTRACT To solve the problem of multi-target hunting by an unmanned surface vehicle (USV) fleet,a hunting algorithm based on multi-agent reinforcement learning is proposed.Firstly,the hunting environment and kinematic model without boundary constraints are built,and the criteria for successful target capture are given.Then,the cooperative hunting problem of a USV fleet is modeled as a decentralized partially observable Markov decision process(Dec-POMDP),and a distributed partially observable multitarget hunting Proximal Policy Optimization(DPOMH-PPO)algorithm applicable to USVs is proposed.In addition,an observation model,a reward function and the action space applicable to multi-target hunting tasks are designed.To deal with the dynamic change of observational feature dimension input by partially observable systems,a feature embedding block is proposed.By combining the two feature compression methods of column-wise max pooling (CMP) and column-wise average-pooling(CAP),observational feature encoding is established.Finally,the centralized training and decentralized execution framework is adopted to complete the training of hunting strategy.Each USV in the fleet shares the same policy and perform actions independently.Simulation experiments have verified the effectiveness of the DPOMH-PPO algorithm in the test scenarios with different numbers of USVs.Moreover,the advantages of the proposed model are comprehensively analyzed from the aspects of algorithm performance,migration effect in task scenarios and self-organization capability after being damaged,the potential deployment and application of DPOMH-PPO in the real environment is verified.

1.Introduction

With the rapid development of unmanned vehicles and intelligent technology,the intelligent combat of unmanned clusters will become a promising battle mode on the future battlefield [1,2].Compared with Unmanned Aerial Vehicles (UAVs),Unmanned Ground Vehicles (UGVs) and other technically mature equipment,the application of USV fleets in autonomous operations is still in the exploratory stage[3-5].In this field,multi-target hunting by a USV fleet is an important aspect of autonomous operations of USVs,involving situation awareness,cooperation,decision-making and control,and rivalry game.

To solve the problem of multi-target hunting by a USV fleet,traditionally,the solution methods mainly include the deterministic approach and the heuristic approach.The former solves the problem using traditional mathematical tools.By building a differential game model of pursuer-evader,the optimal time trajectory and hunting strategy can be calculated [6].Inspired by the hunting behavior in nature,heuristic algorithms simulating wolf hunting [7],predator-prey systems [8]and others have also been proposed.However,in the hunting strategy design,the traditional methods have some limitations as they often make a single assumption about the motion strategy of the escaping target or evader,but it is difficult for one’s own side to know the control strategy of the evader in the real battlefield environment,and when the environment model changes,the controller parameters are difficult to adapt quickly.

With the rapid development of Deep Reinforcement Learning(DRL),artificial intelligence has displayed overwhelming advantages in dealing with complex decision-making and game problems[9],and even outperforms human beings in some fields [10,11].Multi-agent Reinforcement Learning (MARL) is a combination of the Multi-agent System (MAS) and DRL.Under given rules and environmental constraints,through extensive training,agents can show extraordinary intelligence and insight [12,13].With such characteristics,they can give play to the decision-making advantages in the military environment featuring high-intensity game confrontation.The DRL-based unmanned equipment coordination[14]and air combat training system [15]have been preliminarily applied in the U.S.military.

MARL techniques have seen wide applications in target encirclement and capture.For example,Fu et al.[16]proposed the DEMADDPG (decomposed multi-agent deep deterministic policy gradient) algorithm to address the problem of cooperative pursuit with multiple UAVs.Four drones were used to capture the highspeed evaders in the simulation environment.Wang et al.[17]developed a learning-based ring communication network to solve the communication optimization problem in the cooperative pursuit process,which could reduce the communication overhead and meanwhile ensure a high task success rate.Wan et al.[18]introduced a novel adversarial attack trick into agent training by modeling uncertainties of the real world,so as to strengthen training robustness.In terms of the kinematics of non-holonomic constraints,Souza et al.[19]realized the cooperative pursuit of agents using the TD3 algorithm [20],and verified the proposed method by drones in the real world.Hüttenrauch et al.[21]studied the scalability of the homogeneous agents model and developed a state representation method that meets the permutation invariance.The experiments showed that this method could support up to 50 agents to participate in the pursuit-evasion task simultaneously.

However,the majority of references focused on the situation of multiple agents capturing a single target,while the research on cooperative multi-target capture is not sufficient.It is largely due to the increased complexity of the problem where compared to single-target capturing,to capture all targets as soon as possible,the agents need to not only learn to cooperate but also approach appropriate targets according to situational awareness.Additionally,during the multi-target capturing task,an agent needs to cooperate with other nonspecific agents multiple times.In order to reduce the complexity of the problem,Ma et al.[22]utilized task assignment and converted multi-target capture into multiple single-target captures.However,as the evader has mobility in the real world,and the situations of the pursuer and the evader are dynamically evolving in the game environment,the task allocation based on the current state is not necessarily optimal.Yu et al.[23]proposed the distributed multi-agent dueling-DQN algorithm to solve the multi-agent pursuit problem.The encirclement of two intruders by eight pursuers in the MAgent environment [24]was realized,proving that it is technically feasible to use the end-to-end training method to enable pursuers to learn evader selection and cooperative pursuit at the same time.However,since the MAgent environment is based on discrete grid spaces,it ignores the kinematic features of agents,and can only represent the abstract spatial relationship between agents,which cannot be migrated to the real environment.

The existing research findings are largely based on the assumptions of finite boundary constraints and global situational awareness,and thus are difficult to be directly applied to the engineering practice of multi-USV hunting.Firstly,most studies have introduced the hunting boundary constraint [16-19,22,23].When the evader is chased to the regional boundary,it is regarded as successful hunting.Some studies used the periodic toroidal statespace boundary constraint [21].When the agent moves beyond the boundary,it will reappear from the opposite side of the space,which is obviously impossible in the real scenario.Moreover,as there are usually no boundary constraints and maneuvering range restrictions in the marine environment,the USVs cannot drive the target to the edge of the area,but only surround its by themselves,and thus it is more difficult to achieve successful hunting.Secondly,some studies assume that the environment is fully observable[16-18,22].However,in the real battlefield environment,a large number of agents distributed widely in space are involved in the cooperative task.Affected by data processing capabilities and communication distance,each agent is usually unable to obtain the global situation information in the environment,which brings the problem of partial observability.In addition,unmanned platforms in the confrontational environment are required to have the ability to continue to perform tasks when a small number of nodes are damaged.However,the impact of node damage on hunting tasks has not been sufficiently investigated.

Driven by the problems above,a hunting environment model without boundary constraints is built and the criteria for successful USV hunting are given.On this basis,the USV motion model and the evasive maneuver policy of the evader are developed.Then,the multi-USV cooperative hunting problem is modeled as a decentralized partially observable Markov decision process(Dec-POMDP)[25],and a distributed partially observable multi-target hunting Proximal Policy Optimization (DPOMH-PPO) algorithm applicable to USVs is proposed.The observation model based on partial observable conditions is designed,and the information to assist agents in making round-up and capture decisions is extracted.A reward function combining guiding rewards and sparse rewards is constructed,covering the rewards for agents in the whole process from target selection to capture.The action space decoupled from kinematic control of USVs is designed to avoid the involvement of the policy network in the complex coupling relationship between USV kinematic control and the reward function.A policy network and a value network based on feature embedding block are also designed to give the algorithm more flexibility and robustness.Finally,the simulation environment of multi-USV hunting is built,the network training of DPOMH-PPO is completed by using curriculum learning,and the effectiveness of the algorithm is analyzed and compared with other algorithms in terms of performance.

Salient contributions in this paper can be summarized by three aspects:

(1) Proposing a multi-USV cooperative hunting method for multiple targets by using the MARL method to solve problems with continuous,no boundary limits and partial observability in practical applications.

(2) Using the end-to-end training method,designing the state feature and reward function for the whole task process,and realizing the agents’ decision-making processes such as objective allocation and cooperative hunting through a single policy network.

(3) Introducing the feature embedding block applicable to agents under partially observable conditions,which enables the policy network to deal with the observational features of dynamic dimensionality efficiently,thus making the USV fleet more flexible and robust.

The rest of this paper is structured as follows.Section 2 introduces the preliminaries related to the MARL model and algorithm.Section 3 describes the multi-target hunting problem and establishes the kinematic model.Section 4 covers the design details of the DPOMH-PPO algorithm in detail,including multi-agent state space,reward function and action space,network structure and algorithm flow,etc.Section 5 gives the configuration of environment and training parameters,and analyzes the DPOMH-PPO algorithm from several angles.In Section 6,the main conclusions are presented.

2.Preliminaries

2.1. Local observation models

The interaction graph denoted by G=（V，E）is determined by the set of nodesV={v1，v2，…，vN} and the set of edgesEof the agent swarm.E⊂V×Vis represented by the undirected edges in the form of{vi，vj},where agentsiandjare neighbors.G is called a dynamic interaction graph if the set of nodes or the set of edges undergo changes.The neighbors of agentiin the graph G is given by

Within this neighborhood,agentican sense local information about other agents.The information agentireceives from agentjis denoted asoi，j=f（si，sj）,It is a function of the states of agentifor agentj.Only whenj∈NG（i）,observationoi，jis available for agenti.Hence,the complete information set agentireceives from all neighbors is given by

2.2. Decentralized partially observable Markov decision model(Dec-POMDP)

The decentralized partially observable Markov decision process(Dec-POMDP) [25]with shared rewards is investigated.A Dec-POMDP is constructed as 〈S，A，O，O，P，R，N〉,where S is the state space,A is the shared action space for each agent,and O is the set of local observations.O:SN×{1，…，N}→O denotes the observation model,which determines the local observationoi∈O for agentiat a given state s∈SN,namelyoi=O（s，i）,and P :SN×AN×SN→[0，1]denotes the transition probability model from s to s′,given the joint action a∈ANfor allNagents.Finally,R:SN×AN→R represents the global reward function for encoding the cooperative task of the agents by providing an instantaneous reward feedbackR（s，a）according to the current state s and the corresponding joint action a of the agents.

2.3. PPO algorithm

Proximal Policy Optimization [26](PPO) is a reinforcement learning method based on on-policy and actor-critic framework.Originating from Trust Region Policy Optimization (TRPO) algorithm [27],this algorithm reduces the computational complexity and improves the learning performance by modifying the objective function.PPO algorithm takes the probability ratio of the output actions of strategies before and after policy update as its basis.The policy gradient loss function is defined as

3.Problem modeling

3.1. Description of multi-target hunting by USV fleet

Let’s consider the following scenarios.There areNphomogeneous USVs andNpevaders in the boundless sea.The two sides have opposite tactical purposes.The USVs need to cooperate to capture the evaders,and the evaders try to avoid and stay away from the USVs.When an evader is successfully encircled by the USVs,it will be neutralized,and then the USVs can choose to continue to hunt other targets that have not been neutralized.When allNpevaders are neutralized,the task is completed.

The scenario of single-target hunting is shown in Fig.1.

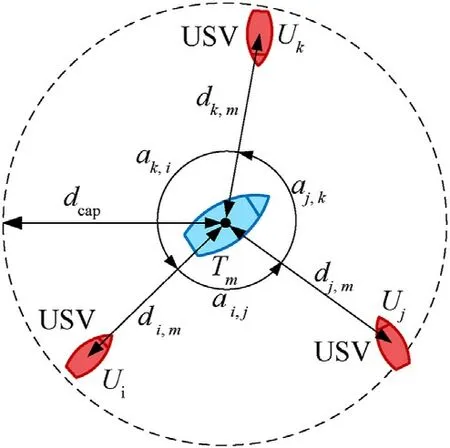
Fig.1.Schematic diagram of single-target hunting.

In Fig.1,Tm（m=1，2，…，Ne）represents for any evader,dcapis the hunting radius,Ui（i=1，2，…，Np）represents the USVs,anddi，kis the distance betweenUiandTm.When the distance between the USV andTmis less than the encirclement radiusdcap,the USV is seen as being in the process of pursuingTm.The encirclement angle αi，jis defined as the included angle ofUiandUjrelative toTmwhen encircling the escaping targetTm.If there are no other USVs between the azimuth angle of two USVs relative toTm,the relationship between the two USVs is defined as neighboring.If among the USVs participating in the pursuit,the encirclement angle between any neighboring USVs is less than αcap,then theTmis successfully captured.αcapis the valid encirclement angle.

Limited by the observation and communication distance,each USV can only obtain the state of the surrounding friendly USVs and the location information of the evaders.It is necessary to establish an effective strategy so that each USV can make maneuver decisions based on the received information,and that the USV fleet can successfully hunt multiple targets in the shortest time possible without collisions between them.

3.2. Kinematic model

For both sides of the pursuer and the evader,the second-order kinematic equation is established as follows:

where（xi，yi）represents the position of any agenti;vi,ψi,ωiare the speed,heading angle and angular velocity respectively;avandaωare acceleration and angular acceleration.Among them,speed viand angular velocity ωiare restricted: -ωmax≤ωi≤ωmax,0 ≤vi≤vmax.Fig.2 shows the coordinate system of the agent.

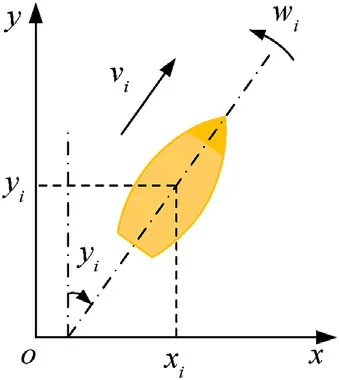
Fig.2.Schematic of the agent coordinate system.

3.3. Strategy of the evader

This paper employs the artificial potential field method,which is commonly used in path planning,as the escape strategy of the evader.It is assumed that each USV applies a repulsive force in the vector direction of the evader,and each repulsive force component decreases with the increasing distance between the USV and the target.The velocity direction vector vmof the evaderTmis expressed as

where pi（xi，yi）and pm（xm，ym）represent the positions of the USViand the evaderTmrespectively.

4.DPOMH-PPO algorithm design

The multi-target cooperative hunting task of the USV fleet can be described as a decentralized partially observable Markov decision model(Dec-POMDP),which is represented by a tuple〈S，A，O，O，P，R，N〉.

The model has two important characteristics: 1) All agents can only observe part of the environment stateoi=O（s，i）via the observation modelO;2) All homogeneous agents share the same policy πθ,and θ is the parameterized policy network weight.To ensure the homogeneity of the system,it is considered that the state transition model P and the observation modelOof the agents are permutation invariant [29].

The polity π of agentiis the mapping probability from local observationoito actionai.At any timet,the state of the system is st∈SN,agentiobtains the local state=O（st，i）according to the observation modelO,and selects the action∈A through the policy π.The system reaches the next state st+1∈SNthrough the state transition model P,and each agent receives the same rewardR（s，a）.The purpose of the reinforcement learning algorithm is to find the optimal policy π*so as to maximize the cumulative discounted rewardRt.

where γ is a parameter,0 ≤γ ≤1,called the discount rate.

In this section,combined with learning in an end-end manner,such components of Dec-POMDP as the observation model,reward function and action space used in the DPOMH-PPO algorithm were first designed,and then the DPOMH-PPO algorithm flow was studied.Finally,the network design was introduced in detail.

4.1. Observation model design

The system state is a complete description of a hunting scenario.Due to the partial observability of the system,an agent cannot obtain all the states and is only able to observe limited information.Thus,it is necessary to establish the observation modelOto convert the partially observable system state into decision information that can be directly used by the agent.

The system state in the hunting problem consists of the position of the USV fleet,motion parameters,the position of the evader and the capture state.And there are two approaches to describe the position feature relations,namely,encoding the information in a multi-channel image within the observation range [24],and concatenating the received state information directly [30].However,both methods have drawbacks.The image information can effectively characterize the relative position relationship,but after pixel discretization,the accuracy of spatial position features is limited,resulting in quantization errors.Although setting a higher image resolution for encoding can reduce discretization errors,it will lead to a nonlinear increase in the computational complexity.In addition,concatenating state information can reduce the computational complexity,but under partially observable conditions,the input dimensionality of neural networks changes dynamically,and the population invariance method must be used to address the problem of observation dimensionality change[21,31].Based on the second feature description approach,an observational feature network for agents which can be used to deal with dynamic input dimensionality is designed to overcome the drawbacks of this method.The network structure is in subsection 4.4.

The designed observational featureoiis composed of friendly observational feature,evader feature,encirclement featureand USV state feature.

4.1.1.Friendly observational feature

Friendly observational features are employed to describe the state of the friendly USVs within the communication rangedpof the agent.The relationship between agents can be modeled as GP=（Vp，Ep）,whereThe observability between agents can be represented by the connectivity of the graph Gp.For agenti,the information of the USV numbered（i）={m｜{Ui，Tm}∈E} can be observed,and the friendly observational feature is defined as

For agenti,the observational feature of the neighboring agentjis set tooi，j={di，j，xi，j，yi，j，Δvi，j，Δvx，Δvy，Qi，j，Qj，i},wheredi，jrepresents the Euclidean distance between the two agents,xi，jandyi，jare the components ofdi，jin the coordinate system,Δvi，j=vi-vjis the relative velocity difference,Δvxand Δvyare the components of Δvi，jin the coordinate system,Qi，jandQj，iare the relative bearing angle between them.Their relationship is shown in Fig.3.

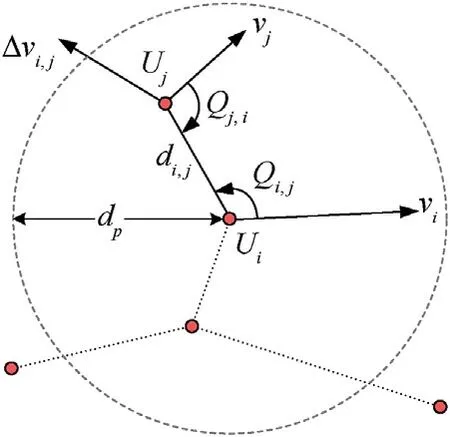
Fig.3.Schematic of friendly USV observational feature.

4.1.2.Observational feature of the evader

Observational features of the evader are to describe the state of the evaders within the observation radiusdeof the USV agent.Similarly,The observation of the target by the agent is modeled as Ge=（V，Ee）,whereV={U1，U2，…，UN，T1，T2，…，TNe},Ee={Ui，For the information of the target numberedthat can be observed by agenti,the observational feature of the evader is defined as

Similarly,for agenti,the observational feature of the evaderTmwithin the observation radiusreis set tooi，m={di，m，xi，m，yi，m，Δvi，m，Δvx，Δvy，Qi，m，Qj，m，κ（m）},and the definition of the feature element is basically the same as that of the friendly observational feature.The last item κ（m）represents the demand function,which refers to the current demand degree of the evaderTmfor USVs in the hunting task,κ（m）∈（-1，1）.The expression is

4.1.3.Encirclement feature

Encirclement features are to describe the optimal position maneuvering trend of the agents in the cooperative state.In the Cartesian coordinate system with the agent as the origin,the orthogonal component can be used to represent the position relationship of the observed targets relative to the agent.This form of position feature can be directly applied to deal with the tracking and formation problems.However,in the capture problem,the agent needs to indirectly understand the cooperative encirclement situation through the relative position information,and then make decisions that facilitate the USVs to form a circular formation around the evader.Obviously,this entails requirements for the strong feature extraction ability of deep networks.In addition,with the same encirclement situation relationship,the position feature is not rotation invariant,which increases the difficulty of network generalization.

To reduce the cost of network learning,this study proceeds from the perspective of feature engineering,extracts the feature of encirclement angle from the encirclement situation,and then decouples it into the Cartesian coordinate components as the encirclement feature,as shown in Fig.4.

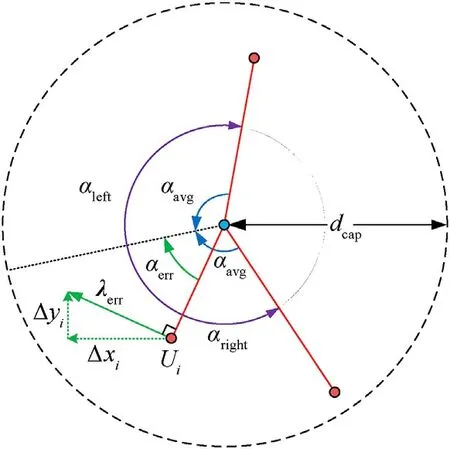
Fig.4.Schematic of encirclement feature.

It is assumed that agentiis within the encirclement radius of the evaderTm.Ifthe encirclement angles of agentiand neighboring USVs are αleftand αright,and the average encirclement angle αavg=（αleft+αright）/2 is defined.Let αerrbe the error angle from agentito the angular bisector,and let λerr∝αerrrepresent the tangential error ofUirelative toTm,which is taken as the observational error of agentiencirclement,λerr={Δxi，Δyi}.Δxiand Δyiare the Cartesian coordinate components of λerr,which reflects the reference error of the tangential component of the target encirclement situation formed by agent i,and the encirclement feature=λerr={Δxi，Δyi} is set.

4.1.4.USV state feature

USV state features describes the state attributes of the agent itself.osi={vx，vy，ax，ay},including the current speed vxand vyof the USV and the action outputaxandayat the previous time.The action design is detailed in Section 4.3.

4.1.5.Observational features

To sum up,the observational featuresoiof agentiare expressed as

In the formulas,the number of elements of the friendly observational featureand of the target observational featurechanges dynamically,which is related to the spatial location and observation range of the agent.The encirclement featureand the USV state featureare one-dimensional vectors with fixed length.

4.2. Reward function design

Based on target capture in Section 3.1,the current state of the agent can be effectively evaluated by designing an appropriate reward function,which combines guiding rewards and sparse rewards.Whenever an evader is captured,the agent participating in the capture will get a one-time reward.During task execution,each agent will receive a guiding reward at each time step,which aims to guide the agents to chase the evader and cooperate to form an encirclement situation.Finally,the average reward of all agents is calculated as the shared reward of the USV fleet.

The reward functionRconsists of capture reward,guiding reward,collision penalty and time consumption penalty by weight,which is defined as

whererk（i）is thek-th reward of agenti.Since agents are homogeneous,rkis used to uniformly refer tork（i）in the rest of the paper.

4.2.1.Capture reward r1

When an evader is successfully captured,the agents participating in the capture will get a reward according to their contribution.The criteria for contribution evaluation is the proportion of the encirclement angles between the agent and the target(i.e.half of the encirclement angle adjacent to the left and right of the agent),expressed byrcapis the coefficient of total capture rewards.To evaluate the circular formation around the target,it is considered that the more consistent the encirclement angles α formed,the more complete the circular formation of the agents around the target.Thus,a reward function coefficient e-k1σ（α）in the form of a negative exponent is established,where σ（α）is the standard deviation of the encirclement angle andk1is the accommodation coefficient.

4.2.2.Guiding reward r2

To guide the agents to approach the evaders in the early stage of training,the agents will receive positive rewards related to the distance to the targets in each time step.In the formula,dtar=represents the distance between an a gent and its nearest target.Whendtar>dcap,the agent enters the enclosed area and obtains a guiding rewardr2=rguide.Whendtar>dcap,the guiding reward coefficientrguidedecreases exponentially with the increasing distance,wherer2=rguidee-k2dtarandk2is the accommodation coefficient.

4.2.3.Collision penalty r3

A negative exponential reward functionr3is established to describe the collision risk between agents,wherercrashis the collision penalty coefficient,represents the shortest distance between agentiand other agents,andk3is the accommodation coefficient.

4.2.4.Time consumption penalty r4

To ensure the timeliness of tasks,the agent will receive a negative returnrtimein each time step.

4.3. Action space design

For kinematic problems,the action space is usually designed as the control input of kinematic systems.The kinematic model of holonomic motion constraints outputs the acceleration vector directly from the policy network [17,30].The kinematic model of non-holonomic motion constraints of UAVs,UGVs and other unmanned systems can be simplified into a first-order system so as to determine the controlled quantities of the policy network’s output speed and angular velocity[18,32].Compared with UAVs and UGVs,the control response of USVs is slow,and thus usually described by a second-order system.The controlled quantities are accelerationavand angular accelerationaω.However,avandaωhave a complex coupling relationship with the reward functionR.Whenavandaω are directly used as network output,it is difficult to guarantee the learning efficiency and convergence of the network.

Considering that the designed observational features are mainly orthogonal components of the coordinate,the action space a designed in this paper is set as the two orthogonal independent controlled quantities in thexandydirections,namely,a={ax，ay}andax，ay∈[-1，1],and then the mapping between action space a and the expected speed vexp/expected direction ψexpof the USV is established:

where vmaxis the maximum USV speed.Finally,the USV tracking control algorithm[33]is introduced to indirectly controlavandaω so that the USV navigates according to the expected navigation parameters.

By avoiding the involvement of the policy network in the complex coupling relationship between the kinematic control and reward function of the USV,the proposed method reduces the decision-making difficulty of the system.

4.4. Network structure design

Due to the partial observability of agents,the number of friendly agents and evaders in the observation range changes dynamically,leading to the uncertainty of the observed dimension features.Thus,it is necessary to design a network structure applicable to the uncertain dimension feature input.In this paper,a feature embedding block based on learning is designed first,and then the structures of the policy network and value network are designed respectively.

4.4.1.Design of feature embedding block

The idea of feature embedding is to encode a variable number of homogeneous state features into features with fixed dimensions.Ref.[21]proposed the method of using neural networks to define the feature space of a mean embedding,which has better information coding performance than the histogram-based method[34]and radial basis functions(RBF)method[35].Based on Ref.[21],we construct a feature embedding block (FEB) applicable to observational features of agents.FEB is designed to apply a network layer with parameter learning capability to each item in the twodimensional observational features of agents,and then further compress the output two-dimensional features into onedimensional features with fixed dimensions.Inspired by the pooling layer in convolutional neural networks,we propose two feature compression methods,maximum pooling and average pooling,and realize feature dimension reduction for the first time.The structure of FEB is presented in Fig.5.

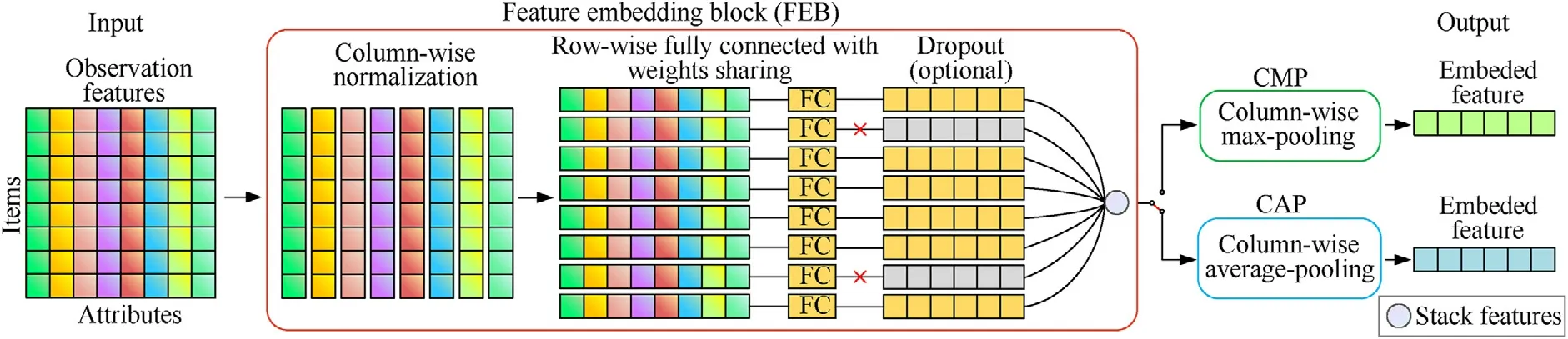
Fig.5.Structural diagram of feature embedded block (FEB).

FEB inputs the observational features.Firstly,the same type of attributes of different items are standardized,so that the observations such as angle and distance are on the same quantitative scale.Then,each item passes through the fully connected layer with the same weight to obtain the features of the same dimension.To improve network robustness,the dropout operation can be added in the last step to randomly mask some observational features.Two feature compression methods,column-wise max-pooling (CMP)and column-wise average-pooling(CAP),are designed.Finally,FEB passes through the CMP or CAP layer to obtain the embedded features.

4.4.2.Policy network structure design

The policy network πθinputs the observational featureoiof the agent as described in Section 4.1.Firstly,the friendly agent’s observational featureand the evader’s observational featureinput two independent FEB respectively.The dropout technique is used for the FEB passed by,which is then processed by the CMP and CAP layers,and four embedded features with 32 dimensions are obtained.Subsequently,they are connected with the encirclement featureand the USV state featureto form a feature vector with a length of 134.Finally,after they are calculated by the twolayer Fully Connected (FC) network and Gated Recurrent Unit(GRU)network respectively,the mean of the Gaussian distribution μ=[μx，μy]and standard deviation σ=[σx，σy]of the controlled quantity a={ax，ay} are output.During training,the controlled quantity can be obtained by sampling the Gaussian distribution.In the evaluation,ax=μx,ay=μy.The policy network structure is shown in Fig.6.

Fig.6.Schematic of policy network structure.

4.4.3.Value network structure design

The value networkVφinputs the set of observations of all agents o=[op，oe，oc，os].The elements in o are the vertical stacking of each agent’s corresponding elements,ocand osrepresent the twodimensional features of theNprow.Different from the policy network,the designed value network concatenates ocand oshorizontally,and after the processing of the feature embedding block,the embedded features with a length of 64 are output.The middle layer structure of the network is consistent with πθ,and finally the network outputs the predicted value of the state valueQ.The value network structure is shown in Fig.7.

Fig.7.Schematic of value network structure.

4.5. Algorithm flow design

As each agent in the multi-agent system is affected by the environment and other agents simultaneously,the single-agent RL algorithm cannot produce ideal effects,and thus it is necessary to use joint state-action space to train the agents.To this end,some centralized training and decentralized execution methods such as MADDPG [30],COMA [36],QMIX [37],and MAPPO [38]have been proposed.Among them,MAPPO (Multi-agent Proximal Policy Optimization) is a variant of Proximal Policy Optimization (PPO)[26]applied to multi-agent tasks.It is an algorithm with the actorcritic architecture and has high learning efficiency under the condition of limited computing resources.It can deliver the performance of the mainstream MARL algorithm by performing only a small amount of hyperparameter search [38],and has demonstrated high effectiveness in a variety of cooperative tasks.Therefore,we use MAPPO as the learning method for the multi-USV cooperative hunting problem.

Based on the PPO algorithm,MAPPO is extended to the scenario of multi-agents by training two independent networks,namely,the policy network πθwith parameter θ and the value networkVφwith parameter φ.They share network weight for all homogeneous agents.The policy network πθmaps the local observationoiof agentito the mean and standard deviation of the continuous action space.The value networkVφ:S →R maps the global state and the state action of agentito the estimate of the current valueQ.In the case of multiple agents,the loss functionLCLIP（θ）is rewritten as

where B is the number of batch processing,N is the number of USVin the fleets,which is the importance sampling weight in the form of multiple agents,is the corresponding advantage function.

Accordingly,the loss functionLCLIP（φ）of the value network is

In the present paper,the centralized learning and decentralized execution(CLDE)framework is used to implement the multi-target hunting by USVs.In the training process,a centralized control center is constructed for obtaining the global state information,which is used to train the agents.In the evaluation process,each agent only needs to make action execution decisions based on its observations,without considering the states and actions of other agents.The framework flowchart is in Fig.8.

Fig.8.Centralized training and decentralized execution framework of USV fleet.

During training,the parallel training environment outputs the global state st,and then the reward functionRand the observation modelOoutput the rewardrand observationoobtained by each USV in this step of training according to st.The USV policy network outputs actionaaccording to the observationo.Finally,the parallel training environment inputs the joint action atof each USV and gives the updated global state st+1,which means completing an interactive cycle.During each cycle,the intermediate state data is stored in the experience replay buffer in the form of[st，ot，ht，π，ht，V，at，rt，st+1，ot+1],where ht，πand ht，Vare the hidden state of Recurrent Neural Network (RNN) in the policy network and value network respectively.When the collected experience reaches the specified capacity,the updated gradient of the policy network and value network is calculated,and the network weights are updated with the Adam optimizer.

Therefore,the testing process is relatively simple.The observation modelOoutputs the observationoof each USV according to the global state st,then the USV outputs actionabased on the observation o,and finally the test environment updates the global state according to the joint action at,which is a complete cycle.

The pseudocode of the algorithm is as follows.

Algorithm 1.DPOMH-PPO algorithm

5.Simulation experiment and analysis

In this section,a multi-target hunting simulation environment is built,the USV policy network is trained with the proposed DPOMHPPO algorithm,and its effectiveness is discussed.Finally,the performance,generalization and robustness of the algorithm are compared and analyzed.

5.1. Experimental environment and parameter setting

The experiment is performed on a workstation with i9-10980XE CPU,RTX2080Ti × 4 GPU(11 GB × 4 VRAM),and 128 GB RAM.Pytorch is used as the deep learning training framework and OpenAI Gym as the reinforcement learning environment framework.A multi-agent runtime environment is built for the cooperative multi-target hunting problem,and the Gym API is redefined.

In particular,the experimental conditions are set as follows:

1) The motion parameters and observation performance of all USVs are consistent,and the escape strategy and motion parameters of all evaders are the same.

Since there is no geographical boundary constraint in the marine environment,a boundary-free experimental environment is established.To ensure the existence of feasible solutions,only the pursuit-evasion scenario of high-speed hunting USVs and lowspeed evaders is considered.

2) At the beginning of each experiment,the USVs are set into an equally spaced formation.In order not to lose generality,the starting position of the target and the orientation of the USVs relative to the target are randomly generated.The schematic of the initial state of the environment is shown in Fig.9.

Fig.9.Schematic of starting position in the simulation environment.

3) Simulation environment parameters are set as shown in Table 1.

Table 1 Parameters setting for simulation environment.

4) After multiple experiments and parameter tuning,the parameters of the reward function in DPOMH-PPO are determined as shown in Table 2

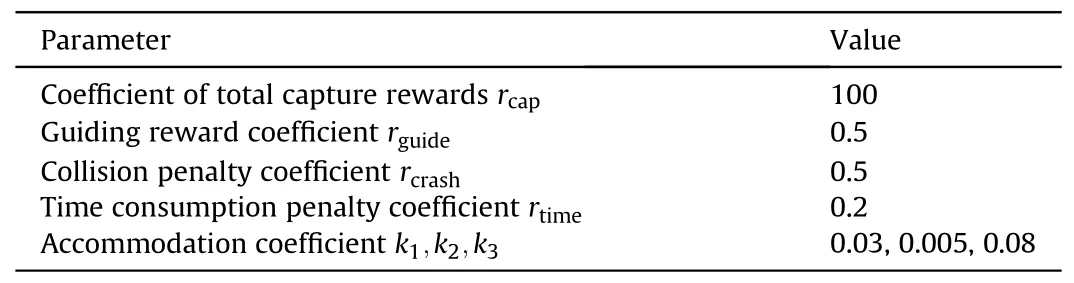
Table 2 Setting of reward function parameters.

5) During network training,curriculum learning is employed to alleviate the sparse reward problem.First,we start the training with a simple hunting task,and then gradually increase the task difficulty to the level of actual difficulty.The factors determining the difficulty of the hunting problem include the speed of the evader and the encirclement radiusdcap.In the early stage of training,the target speed is reduced and the encirclement radius is increased so that the USVs can easily obtain rewards and have sufficient exploration opportunities.Such a method facilitates USVs to perform more complex cooperative behaviors.After multiple experiments and hyperparameter tuning,the hyperparameter setting for the training of DPOMH-PPO is determined as shown in Table 3

Table 3 DPOMH-PPO hyperparameter setting.

5.2. Effectiveness analysis of DPOMH-PPO

5.2.1.Effectiveness analysis for different numbers of USVs

This section evaluates the effectiveness of DPOMH-PPO under different initial USVs numbers.Since the state feature design is scalable,theoretically,only one USV number is needed for training,and then the weight of its policy network can be compatible with any number of USVs in the cooperative hunting tasks.However,to make comparisons of algorithm performance,the number of USVs is set to 6,8,10,…,24(the number of targets is set to be half of the number of USVs),and the training is completed independently for each case,which corresponds to the optimal strategies in 9 cases respectively.Theoretically,the number of USVs can be larger,but considering the VRAM limit,the maximum number of USVs for training is 24.

To ensure the reliability of the results,we use different random seeds to train each case for 5 times,and the number of training steps in each experiment is 6 million.Among them,the reward curves for three hunting scenarios,namely,6 USVs encircling 3 targets,12 USVs encircling 6 targets,and 24 USVs encircling 12 targets (hereinafter abbreviated asNpvsNe,representing the number of USVs and targets)are shown in Fig.10.

Fig.10.Reward curves of DPOMH-PPO algorithm in different scenarios.

Fig.11.6 USVs vs 3 Targets hunting process: (a) Test scenario 1;(b) Test scenario 2.

Fig.12.12 USVs vs 6 Targets hunting process: (a) Test scenario 1;(b) Test scenario 2.

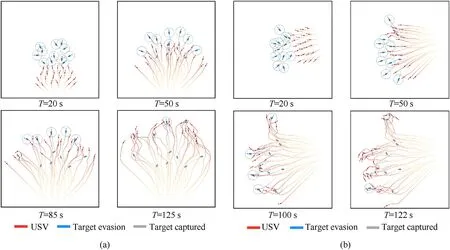
Fig.13.24 USVs vs 12 Targets hunting process: (a) Test scenario 1;(b) Test scenario 2.

As can be seen from Fig.10,the average reward per step increases rapidly in the first 1 million steps,then gradually stabilizes and converges after 2 million steps.When the training is finished,it can be observed that the average reward per step decreases as the problem scale increases.This is due to the increased number of USVs leading to a larger average distance between the USV fleet and the evader at the initial time,thus increasing time consumption.In addition,the USVs are constrained by partial observability and can only rely on local information to make decisions.With the increase of the number of pursuers and evaders,the agents are distributed in a wider spatial range,and the information obtained by the USV becomes more incomplete,so the quality of decision-making outcomes is reduced.

Figs.11-13 shows the sample data records of 6 VS 3,12 VS 6,and 24 VS 12 scenarios.The red and blue vessels in the figures represent the USVs and targets respectively.The red and blue tapered lines stand for the trajectories of the USVs and targets respectively,which reflect the temporal relationship of the trajectories of the two sides.When any evader meets the hunting conditions (the USVs enter the dotted line area and the effective encirclement angle is less than π),the target is incapacitated (shown in gray in the figure).When all the targets are successfully encircled,the task is finished immediately.

From the trajectories in Fig.11(a),it can be found that the USVs can preferentially select their nearest targets (T=45 s) and cooperate to encircle the target.When it is successfully captured,the USVs will immediately turn to pursing the next target (T=60 s).From the trajectories of the USVs in Fig.11(b),it is found that the USVs have learned to surpass the target from the rear side to intercept the target and force it to turn (T=85 s),thus creating a good opportunity for the subsequent encircling by friendly USVs.

Observing Figs.12 and 13,we see that facing more complex situations,the USV fleet can still successfully capture all the targets through cooperation.With the increase of the problem scale,the time required for capture increases as well.DPOMH-PPO can achieve the cooperative hunting of multiple targets by USV fleets under the scenarios of different numbers of USVs and targets.

5.2.2.Ablation experiment

To investigate the effects of the feature embedding block (FEB)and network structure parameters on the performance of DPOMHPPO,an ablation experiment is designed.Based on the network structure designed originally,the contribution of each function to the algorithm’s performance is compared by masking certain structures or adjusting the parameters of the networks.The experimental scenario is set to 12 USVs vs 6 Targets,and the experimental results are listed in Table 4.It can be concluded that the dropout method,CMP and CAP layers involved in the FEB can improve the algorithm’s performance,of which the CAP layer has the most notable contribution,with an ablation loss of 11.64%;the contribution of curriculum learning accounts for 8.22%;halving the feature size will reduce the average reward per step by 9.59%,and conversely,it will be increased by 7.53%;although increased feature size leads to improved rewards,the network training time and computational complexity will be doubled as well.Ablation experiments have further verified the effectiveness of the proposed DPOMH-PPO algorithm.

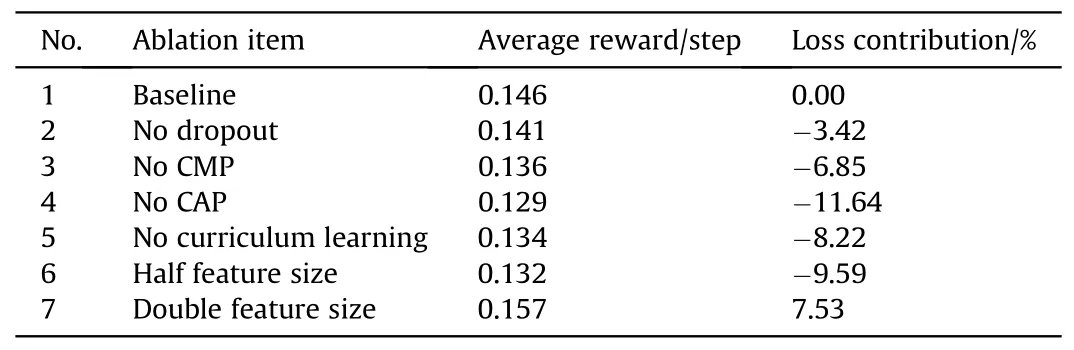
Table 4 Results of ablation experiments.

5.3. Comparative analysis of methods

5.3.1.Performance comparison of algorithms

In this study,three other algorithms are also selected to compare with DPOMH-PPO,including the IL (independent learning) version of DPOMH-PPO,histogram method [34]and Minimap method [24].The IL method uses the traditional singleagent PPO algorithm,where the input of the value network and the policy network is the same,and other parameters are the same.The histogram method maps the observed target position to the range-azimuth 2D mesh,where the mesh size and distance resolution are set to 20 × 24 and 20 m/unit mesh.By referring to the spatial position representation in the MAgent environment,the Minimap method maps target observations to Minimap images with USV as the origin,where the image size and distance resolution are set to 21×21 pixels and 40 m/pixel.These methods have completed training in 9 test environments with the number of USVs ranging from 6 to 24.Then the algorithms’ performance is evaluated from two aspects,average reward per step and average task completion time.Using the average reward per step,the algorithm’s performance can be directly compared,and the larger the average reward per step,the better the performance.The average task completion time reflects the algorithm’s efficiency in performing the cooperative hunting task,and the less time the algorithm takes,the better the performance.

Fig.14 shows the reward curves of 6 VS 3,12 VS 6,and 24 VS 12 respectively.As illustrated,all methods can converge within the training steps,and the average reward per step of DPOMH is the highest in all scenarios;the performance of the IL method is close to that of DPOMH but the gap between them obviously widens as the problem scale increases,which can be explained by the fact that independent learning cannot obtain joint state information,so the variance of the gradient in value network training becomes larger;in term of the average reward per step,Minimap and Histogram is inferior to DPOMH,and in terms of convergence speed,Minimap is faster than Histogram,but at the end of training,Histogram’s performance slightly oversteps that of Minimap.

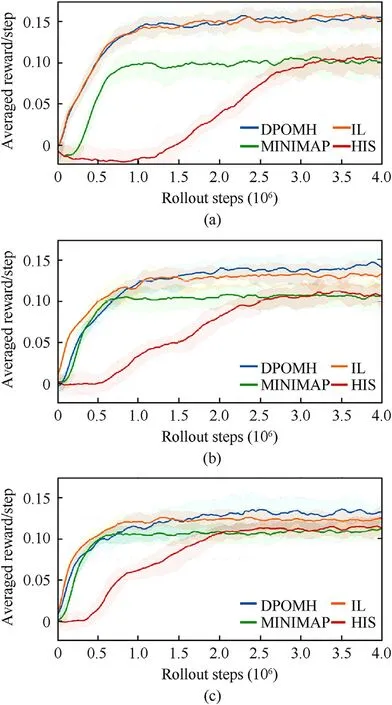
Fig.14.Comparison of reward curves of training of different multi-target hunting algorithms: (a) 6 VS 3;(b) 12 VS 6;(c) 24 VS 12.

Fig.15 further shows the variation of average reward per step and average task completion time of the four algorithms under different initial numbers of USVs.As can be seen from Fig.15(a),with the increasing number of USVs,the average reward per step of the DPOMH and IL methods decreases slowly,while that of the other two methods increases gradually;the average reward per step of DPOMH is always better than that of the other methods,which is consistent with the results shown in Fig.14.Fig.15(b)presents the change in the task completion time with the number of USVs.As the number of USVs increases,the time taken by the four methods all increases monotonously,and DPOMH completes the task in the shortest time.It can be found that the task completion time is negatively correlated with the average reward per step,which can be explained by the fact that long task time means more time penalties received by agents.

Fig.15.Comparison of performance indexes of different algorithms: (a) Average reward per step;(b) Average task completion time.

5.3.2.Generalization performance analysis

To further investigate the multi-scenario migration capability of DPOMH-PPO,the method adopted in this study is to migrate the learned hunting strategy to a larger test environment than during training,and then the changes in performance indexes such as average reward per step and average task completion time are analyzed and compared.In the experiments,the optimal strategies of the four methods for the scenario of 12 VS 6 are selected and then replicated for deployment in the test scenarios of 24 VS 12,36 VS 18,and 48 VS 24 respectively.The comparison of performance indexes is presented in Fig.16.As shown in Fig.16(a),as the problem scale doubles,the average reward per step gradually decreases,but DPOMH-PPO performs better than the other methods in each scenario,and the performance of HIS decreases most significantly.The shortest task completion time is seen in the DPOMH-PPO as shown in Fig.16(b),indicating that DPOMH-PPO possesses better generalization performance.

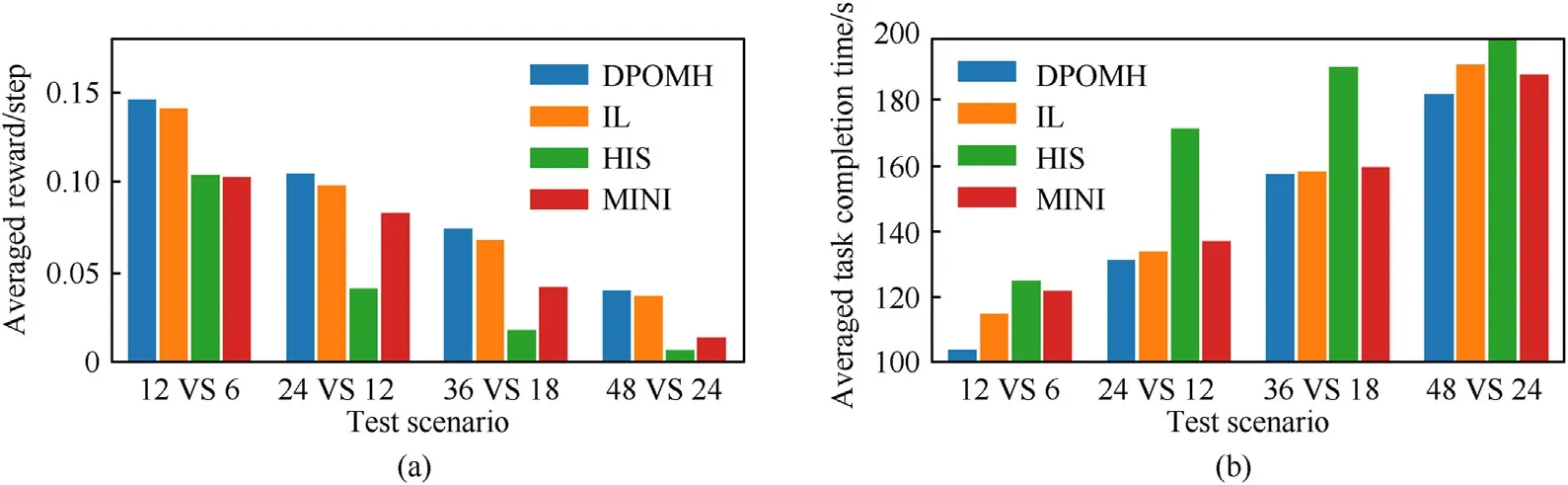
Fig.16.Comparison of generalization performance of different algorithms: (a) Average reward per step;(b) Average task completion time.

5.3.3.Robustness analysis

To analyze the robustness of the algorithms,the damage of USVs is simulated by means of node failure.Specifically,USVs are randomly selected every other period in the hunting process;the throttle and rudder angle control are set to 0,and the observability of the damaged USV is blocked.In this way,the self-organization and flexible coordination capabilities of the USV fleet in the case of suffering damage can be verified.The experiment takes the 12 VS 6 test scenario as the baseline.From the beginning of the task,one USV in the fleet is randomly selected to fail every 15 s until the total number of failed USVs reaches the preset loss limit.

The averaged time consumption in various algorithms for USVs failed in different cases is shown in Table 5.It can be observed that with the increasing number of failed USVs,the task completion time of the four methods increases significantly,and that the time taken by DPOMH-PPO is the shortest under the same conditions.

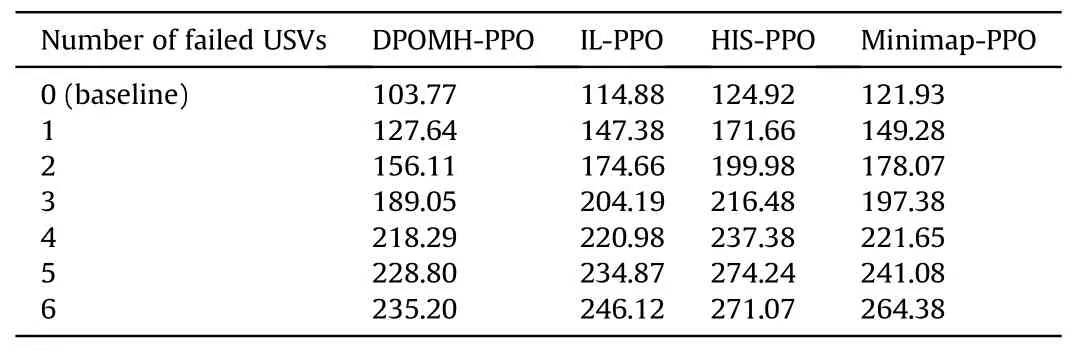
Table 5 Task completion time of different algorithms with USVs failed (Unit:s).

The reward and efficiency of different algorithms are listed in Table 6.The step reward refers to the average reward per step obtained by the active USVs.The efficiency is defined as the ratio of the current step reward to the baseline step reward,which represents the performance of the method after certain USVs have failed.Under the same number of removed agents,the higher efficiency of the algorithm means stronger robustness.As can be seen from Table 6,DPOMH-PPO has the highest efficiency and HIS-PPO has the lowest efficiency under different number of failed USVs.Combining Tables 5 and 6,we find that DPOMH-PPO has the strongest robustness.

Table 6 Step reward and efficiency of different algorithms under different number of failed USVs.

The record of the sample data of DPOMH-PPO during the hunting process with 6 USVs failed is shown in Fig.17.In the figure,the gradually changing trajectories of each agent are retained for 100 s,the yellow USV indicates that it is in the inactive state,and the deactivation time of the USV(T=15 s,30 s,…,90 s)is marked by a purple circle.From Fig.17,we can see that when a friendly USV is inactivated,the other USVs actively gather (T=90 s),and then reselect targets (T=120 s).Three USVs in the middle encircle the target in the middle nearby (T=152 s,170 s);two USVs navigate north and expel a target south (T=152 s,170 s,205 s);one USV navigates south and expels a target north(T=152 s,170 s).Finally,the last six USVs cooperatively hunt all the other targets atT=227 s.It shows that DPOMH-PPO has strong adaptability and possesses the ability to continue to perform the task when half of the USVs are removed.

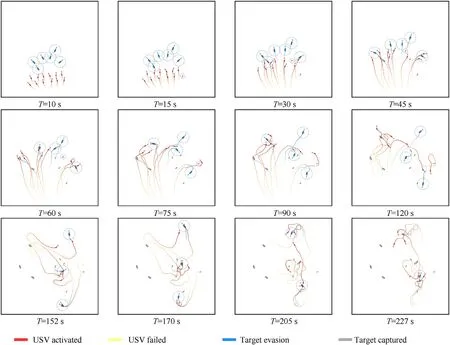
Fig.17.DPOMH-PPO’s multi-target hunting process in the case of 6 USVs failed.

6.Conclusions

To deal with the problem of a USV fleet hunting multiple targets,based on the idea of USV’s autonomous decision-making during operations,the DPOMH-PPO algorithm was developed.Through the comprehensive analysis of the encirclement and capture scenarios,the problem was modeled as Dec-POMDP,and then rational observation space,reward function,action space and network structure were designed.Finally,the simulation environment was built,and the USV fleet hunting strategy was trained with the centralized training and decentralized execution framework.The experimental results show that:

1) DPOMH-PPO can make the USVs in a fleet learn and cooperate in different test scenarios with different numbers of agents,and complete the multi-target hunting task quickly and effectively.

2) The ablation experiment proved that the feature embedded block involving CAP and CMP layers proposed in this work was the key to the performance improvement of the algorithms,and the contribution of the CAP layer was prominent.

3) Compared with the other algorithms,DPOMH-PPO shows obvious advantages in learning efficiency,generalization and robustness,and has the potential to promote practical applications.

A limitation of the current work is that we adopted a regularized escape strategy.This can be improved by implementing the target as an RL agent and training both sides simultaneously similar to Ref.[13].In the future,scenarios near the coastline or islands,and heterogeneous USVs cooperative hunting control will be explored.

In addition,we aim to consider more realistic applications,and further explore the sim-to-real transfer and real-world applications to the multi-agent systems such as UAVs.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors would like to acknowledge the financial support from National Natural Science Foundation of China(Grant No.61601491),Natural Science Foundation of Hubei Province,China(Grant No.2018CFC865) and Military Research Project of China(-Grant No.YJ2020B117).