V 型球调节阀涡流噪声模拟及降噪设计

2023-12-06肖直坤于新海张嵩逸陈时健

流体机械 2023年10期

王宁，肖直坤，于新海，张嵩逸，陈时健，刘平

（1.华东理工大学机械与动力工工程学院，上海 200237；2.中核苏阀科技实业股份有限公司，江苏苏州 215129）

0 引言

调节阀在工业管路系统中应用十分广泛，其产生的噪声也是管路系统噪声的重要组成成分。由于调节阀中节流过程加剧了湍流的不稳定性，它与阀门结构之间的流固耦合可引起新的扰动，因此成为管路系统中的高噪声源［1］。相关研究表明，在大型管道系统的调节阀附近，噪声可达100 dB 左右。这种高噪声一方面危害在此环境下工作人员的身心健康，另一方面噪声伴随的剧烈振动加剧了调节阀及其邻近管路的损坏，使工业生产及人员安全面临风险［2-3］。调节阀噪声主要包含两大类：机械噪声和流体动力学噪声。流体动力学噪声又叫流致振动噪声，根据调节阀不同的工作状态分为涡流噪声、气蚀噪声、湍流激振噪声、水锤噪声［4］。试验表明涡流噪声是阀门流道内流体动力学噪声的主要来源［5］。基于大涡模拟（LES）/Lighthill 混合模拟方法的调节阀流致噪声计算已经有诸多报道，聂欣等［6］对直筒笼式阀门进行了流动噪声模拟计算，得到的模拟结果与实验结果相差在6%以内，证明了该混合模拟方法的准确性。孙长周等［7］采用LES/Lighthill 混合模拟方法对调节阀进行了内部流场与外部声场计算，针对噪声问题设计了多孔内芯，降低了阀门噪声。陈国顺等［8］对气动调节阀的噪声进行了预测，得到了特定流量下阀门开度与阀门噪声的对应关系。戴光等［9］对闸阀气体内漏声场进行了数值模拟，为阀门内漏声学检测提供了方法依据。

目前调节阀涡流噪声的模拟多是针对套筒式、笼式、迷宫式、轴流式调节阀，关于V 型球调节阀涡流噪声计算的相关报道缺乏。相对于其他种类的调节阀，V 型球调节阀具有如下的优点：流道简单、流阻较小，因而流通能力较大；可调比达到300：1；具有较高的密封等级；当球芯相对于阀座旋转时具有较强的剪切作用，因此尤其适用于带有纤维和微小颗粒介质的调节控制。为此，本文利用LES/Lighthill 混合模拟方法对V 型球调节阀涡流噪声进行了数值模拟，并基于涡声理论探究了V 型球阀芯的开孔参数对噪声的影响，大幅降低了V 型球调节阀的涡流噪声，本文的研究为低噪声V 型球调节阀的设计提供了计算方法和优化方向。

1 理论方法

1.1 大涡模拟模型

LES 模型使用的是亚网格尺度湍流模型（SubGrid-Scale-Model，SGS），运用网格尺寸筛选湍流涡。涡的尺寸大于网格尺寸时，运用数值方法直接求解N-S 方程。涡的尺寸小于网格尺寸时，通过各向同性模拟，并引入附加应力项，体现出小涡对大涡的影响。SMAGORINSKY［10］最早提出SGS 模型，后来的学者LILLY［11］和GERMANO等［12］提出了动态Smagorinsky-Lilly 模型，NICOUD等［13］提出了LES WALE 模型。大涡模拟经过修正的控制方程可表述为：

其中，τij为亚网格尺度湍流应力：

式中，u 为速度；t 为时间；p 为压力；ρ为密度；xi为空间坐标；v 为运动黏度；下标i，j 分别为笛卡尔坐标系的不同方向；顶部符号“—”表示空间平均。

1.2 Lighthill 方程

Lighthill 方程［14］从N-S 方程出发，没有经过假设和简化，左边表示为与经典声学波动方程相同的形式，作为求解项。把由于流体引起的波动项移到右边，作为声源项。Lightill 声比拟方程可表示为：

式中，Tij为Lighthill 应力张量；ρ为流体密度；eij为黏性应力张量；δij为单位张量；P 为流体压力；P0为流体平均值；c0为当地音速；ρ0为流体平均密度；x 为笛卡尔坐标量；下标i，j=1，2，3 分别为笛卡尔坐标系的三个坐标轴。在大部分情况下，对于方程中的Lighthill 应力张量由于黏性应力张量引起的声源贡献量很小，噪声主要由雷诺应力项ρuiuj引起，因此在大部分的噪声研究仅考虑ρuiuj的贡献部分。

2 研究对象及计算方案

2.1 研究对象及物理模型

本文计算的V 型球调节阀的三维结构如图1所示，主要部件包括阀体、上阀杆、V 型球（开有贯通的众多小孔）、固定轴、开度指示等。该阀门通过上阀杆的转动，带动阀球转动到指定开度，完成流量的调节。

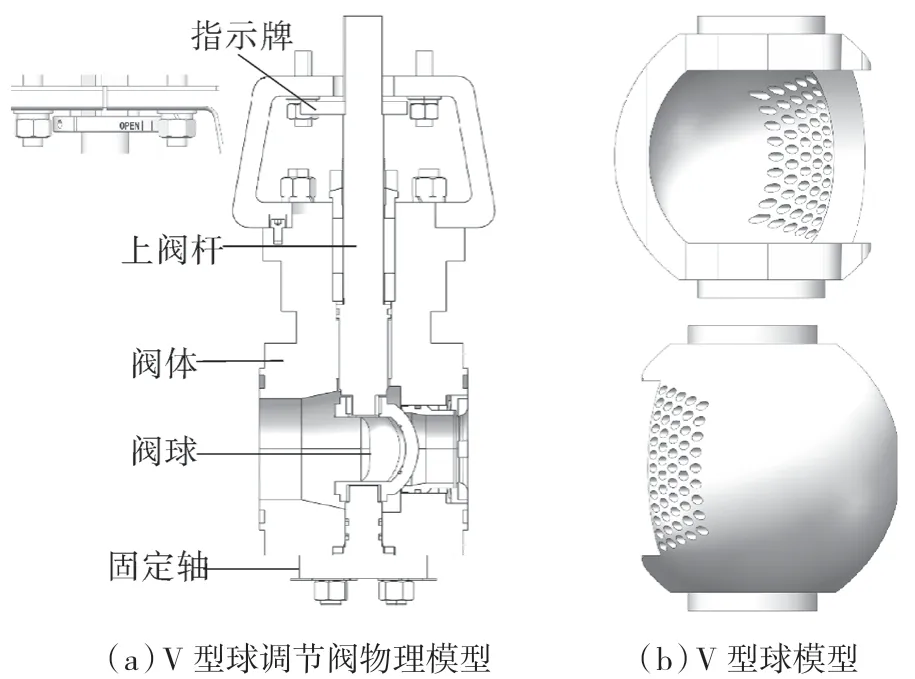
图1 阀门及阀球三维物理模型Fig.1 Three-dimensional physical model of valve and valve ball

2.2 流场计算

根据调节阀物理模型，抽取出调节阀内部流道。为避免回流对阀门出口流动的影响，需将阀门进出口流道延长。流场计算区域包括出入口管道、阀体内部流道。考虑到阀体内部流道的复杂性，现采用非结构化网格对流道进行网格划分，使用Fluent Meshing 软件对流道进行网格划分。阀门最大开度为100%。为达到5 t/h 的流量，将阀门开度设置为30%，出、入口均为压力边界，分别为3.5，1.8 MPa，其他表面设置为壁面，介质为常温水。为保证计算精度，进行网格无关性验证，表1 为网格无关性相关数据。图2 为表1 的4 种网格划分结果，当网格数达到85 万后，稳态出口流量稳定，最终确定网格数量在约90 万，选择图2（c）的网格，在保证计算精度的情况下，节约计算资源。

表1 网格数对V 型球调节阀出口流量的影响Tab.1 Effect of grid number on the flowrate at the outlet of V-shaped ball regulating valve

图2 网格划分Fig.2 Grid division

边界层对流场计算的影响可通过y+值来研究。y+是一个无量纲值，y+=yuτ/ν，其中y 表示第一层网格节点到壁面的距离，uτ表示摩擦速度，ν表示流体粘度。标准壁面函数中，在高雷诺数流动情况下，通常y+值需在30～300 之间，使得第一层网格节点分布于湍流充分发展区域［15］。图3（a）为边界层划分网格。图3（b）为流场的雷诺数分布，可见流体处于高雷诺数湍流流动。图3（c）为流场坐标示意。图3（d）为y+分布，可见在管道区域第一层边界层划分满足y+在30～300的范围内，网格节点处于湍流的充分发展区。在阀门所在区域，y+在0～500，这是由于流道结构复杂，流速变化大，难以对整个阀门的边界层进行划分以满足y+在30～300 的要求。由此带来的计算偏差由相应的试验结果与模拟结果的对此加以考核。

图3 边界层划分Fig.3 Division of boundary layer

流场计算分为2 个步骤，先算稳态流场再计算瞬态流场。计算稳态流场时，选择标准k-ε模型。由图3（b）可见节流后的流体处于完全湍流状态，标准k-ε模型可以兼顾计算精度以及计算效率。收敛残差值选择为10-5。在进行瞬态流场计算时，选用LES 大涡模拟模型。人耳对1 000～3 000 Hz的声音最为敏感，将声学数值模拟结果最高频率fmax定为8 000 Hz，最低频率fmin定为50 Hz，频率间隔定为50 Hz。根据采样定理［16］，通过公式（6）可求得相应计算所需参数。

式中，Δt 为时间步长，N 为计算时间步。

时间步长选择为6.25×10-5s，时间步数选择为320 步。经过2.5 s 后，流场进、出口质量流量差值小于0.5%，流场波动平稳，输出后续320 步瞬态流场结果作为声场计算的声源信息。

2.3 声场计算

根据Powell 的涡声理论［17］，低马赫数条件下的等熵绝热流体的辐射声场基本且唯一的源是涡，所以管道噪声一部分来自流体辐射的噪声与固体壁面的声固耦合作用。此外，由于流体和固体边界的流固耦合作用，导致固体边界振动也会形成噪声。在进行声场计算时，分为两个部分，一部分为声固耦合作用引起壁面振动产生的噪声，另一部分为流固耦合作用引起壁面振动产生的噪声［18-20］。由于流体所引起的固体边界形变量较小，对流场影响不大，所以认为耦合作用是单向的，声场计算步骤如图4 所示。首先从流场提取声源信息，再进行流场网格到声场网格的插值，最后进行流致噪声计算。

图4 声场计算流程Fig.4 Flow chart of sound field calculation

2.4 噪声测试试验

通过开展阀门相关试验来验证仿真计算结果。噪声检测装备和试验装置为功率放大器（PM 0084，深圳市美格信测控技术有限公司）、传声器（GRAS 46BD，丹麦）和采集卡（NI 9250，美国）提供电源，将传声器安装于指定位置测量噪声。试验系统如图5 所示。

图5 试验系统示意Fig.5 Schematic diagram of experimental setup

3 结果分析

3.1 流场结果分析

非稳态流场计算结果如图6 所示。

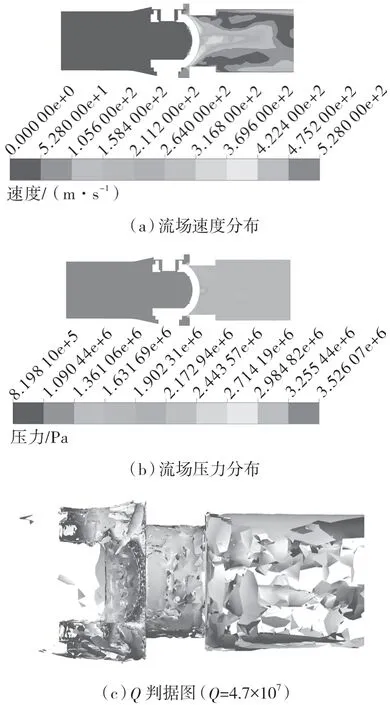
图6 2 mm 孔径阀球非稳态流场Fig.6 Unsteady flow field of V-shaped ball regulating valve with 2 mm bore

由图6（a）可见，流体经过V 型球的节流作用以后在阀球小孔处引起流体的脉动，出现流速突然增大的现象。在阀球小孔处，脉动现象明显，随着流动发展流速趋于平缓。由图6（b）可见，经过V 型球节流后的流体压力损失严重，压力剧烈下降。由图6（c）可见，流体在经过V 型球后，形成了大量漩涡，这些漩涡是导致噪声产生的主要原因。

3.2 内声场分析

求解内声场的步骤是将非稳态流场的计算结果，通过积分插值得到时域的声源信息，再通过傅里叶变换，将时域声源转化为频域声源。在ACTRAN 商业软件中对模型进行如图7 所示的设置。声音会经过管道并沿管道模态面传播，管道模态面为无反射边界，加长的声传播区是用于模拟声音在管道中传播。为保证能够将声源信息插值到声场网格上而不发生数据遗漏，声场网格需要保证每一个波长范围内至少有6 个网格。

图7 内部声场计算模型Fig.7 Internal sound field calculation model

为比较内部声场不同部位噪声频谱特性，需要设置监测点。由图6（c）可知，阀球小孔后有较多漩涡，而其他部位漩涡较少，所以设置如图8所示的监测点，在管道入口处设置监测点IN，阀球小孔前设置监测点M1，小孔后设置监测点M2，管道出口处设置监测点OUT。

图8 内声场监测点设置Fig.8 Internal sound field monitoring point setup

各监测点声压级的频谱曲线如图9 所示。各点声压级随着频率的上升呈下降趋势，高声压级频率集中在0～1 200 Hz。点IN 处的声压级在多个频段高于点OUT 处。对比M1 点和M2 点可以发现，M2 点的声压级在整个频段均大于M1，在图6 中V 型球后观察到较大尺度的旋涡，这种声压级分布趋势符合涡声理论。

图9 2 mm 孔径V 型阀球内声场监测点声压频谱Fig.9 Sound pressure spectra of monitoring points in the internal sound field of V-shaped ball regulating valve with 2 mm bore

3.3 管道外部声场分析

将声固耦合作用引起的壁面振动（AWPF）以及流固耦合作用引起的壁面振动（TWPF）作为激励加载到壁面上，可以计算得到外声场分布情况，如图10 所示，包括三维的声传播区、加载激励的二维壁面、作为无反射边界的二维无限元面以及监测点E。

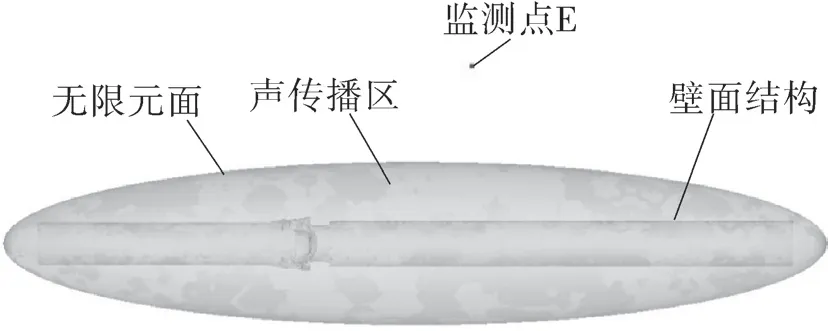
图10 外声场计算模型Fig.10 Calculation model of external sound field

壁面结构的材料选择316 不锈钢，密度为7 930 kg/m3，杨氏模量为1.95×1011N/m2，泊松比为0.3，厚度为10 mm。图11 为监测点E 的声压频谱，包括单独加载AWPF 激励、TWPF 激励和AWPF，TWPF 共同激励的结果。从图11 可以看出，在点E 处，由AWPF 激励引起的噪声声压级在大部分频段大于由TWPF 作用引起的振动噪声。

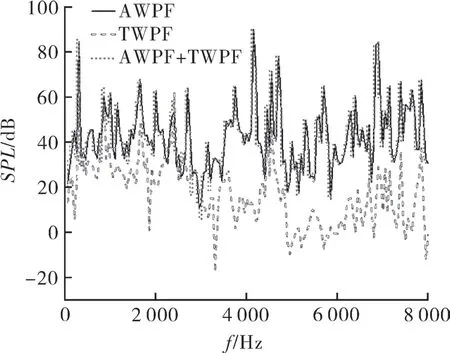
图11 2 mm 孔径V 型阀球监测点E 在各激励下的声压级频谱Fig.11 Spectra of sound pressure level at the monitoring point E of V-shaped ball regulating valve with 2 mm bore under various excitations

2 种激励同时作用时，点E 的频谱曲线由AWPF 激励作用的噪声主导。通过公式（7）可以得到由人耳听感修正的A 计权声压级，由1/3 倍频程声压级计算：

式中，Li为第i 频程的声压级，由1/3 倍频程计算得出；Ai为1/3 倍频程下第i 频程声压级的修正值，数值可从国际标准IEC 61672：2014 中查询A 计权声压修正值表。

通过计算2 种激励共同作用下的A 计权声压级，得到E 点处的A 计权声压级为109.79 dB（A）。作为对此外声场计算结果的验证，本文根据标准IEC 60534-8-3：2000 计算了相同工况和模型下的V 型球调节阀的外声场噪声，得到点E 处噪声为111.02 dB（A），模拟结果与计算结果仅相差1%。此外，表2 为监测点E 处试验数据与仿真数据对比，可见仿真结果与试验结果误差在1%以内，仿真模拟结果是准确的。

表2 监测点E 处试验数据与仿真数据对比Tab.2 Comparison of experimental data and simulation data at monitoring point E

4 开孔参数影响

由图6（c）可知V 型球后产生大量涡，导致涡流噪声。在保证调节阀流通能力基本不变的前提下，对V 型球开孔参数对噪声的影响进行了探究。方案1 为将原来2 mm 的孔径增大到2.4 mm（见图12），方案2 则是从阀球侧面开V 型孔（见图13）。

图12 2.4 mm 孔径阀球Fig.12 Valve ball with 2.4 mm bore

图13 侧面V 型孔阀球Fig.13 Valve ball with V-shaped bore at the side of the ball

根据GBT 17213.2，为保证不同方案的阀门流通能力相同，通过FLUENT 软件对3 种V 型球进行流场分析。稳态流场模拟模型选用标准k-ε模型，阀门流通能力通过Kv值表示。Kv值计算公式为：

式中，Q 为常温水的体积流量，m3/h；p1为阀前压力，kPa；p2为阀后压力，kPa；ρ为流体密度，kg/m3。

表2 为3 种V 形球调节阀不同开度下的Kv值，Kv值差异小于2%，2 种改进方案对阀门流通能力影响可忽略。

表2 3 种V 型球调节阀的开度及对应的Kv 值Tab.2 Opening and Kv value of three V-shaped ball regulating valves

在边界条件不变的情况下，2 种改进阀球阀门的流场Q 判据如图14 所示。发现流体流经阀球后，形成的漩涡有所减少，尺度也相对减小。根据涡声理论，初步判定该改进方法可以降低流致噪声。

图14 Q 判据对比（Q=4.7×107）Fig.14 Comparison diagram of Q criteria（Q=4.7×107）

由图15 可知阀门内流场4 个监测点中M2 处声压最大，故比较改进前后M2 点处内声场声压级情况。从图15 中可见，阀球改进后的2 种阀门噪声在0～8 000 Hz 频段均呈现下降趋势。对于2.4 mm 孔径阀球来说，整个频段上的噪声声压级比改进之前总体较小，峰值噪声频率有所偏移。对于侧面V 型孔阀球来说，在0～4 000 Hz 频段降噪幅度较小，噪声声压级基本与改进前持平。在4 000～8 000 Hz 频段，降噪效果较为明显。

图15 3 种V 型球调节阀M2 点内声场声压级Fig.15 Sound pressure levels of internal sound fields at M2 point for three V-shaped ball regulating valves

由图11 可知外声场监测点的声压级在大部分频段都由AWPF 激励主导，但是考虑到分析的准确性，分析外声场监测点频谱特性时，仍同时考虑了AWPF与TWPF两种激励共同作用下的结果。图16为监测点E处的3种阀球阀门的声压级对比。可以看出，侧面V 型孔阀球在整个频段的声压级均低于改进前，有一些峰值声压级较高，但是并不明显且数量较少。2.4 mm 孔径阀球在整个频段内的声压均低于改进前，只有少部分频率的峰值声压有所上升。经过式（7）计算出2.4 mm 孔径方案阀球在E 点处的声压级为99.23 dB（A），侧面V 型孔阀球E 点处的声压级为98.42 dB（A），相对于改进前的109.79 dB（A），监测点E 处声压级均下降了约10 dB（A）。