基于动网格的轴流式止回阀关闭过程动态特性分析

李树勋，刘斌才，吴翰林，沈恒云，刘太雨

（1.兰州理工大学 石油化工学院，兰州 730050；2.机械工业泵及特殊阀门工程研究中心，兰州 730050）

0 引言

轴流式止回阀具有结构紧凑、流体阻力小、工作过程无能耗、安装灵活等优点，广泛应用于LNG接收站间歇性操作系统、高压系统、泵出口管线等。轴流式止回阀在正常工作工况下一般不会出现问题，但是在事故工况下紧急关闭时，介质流速的急剧变化会造成管道中的介质压力迅速、反复地变化，这样可能引发水锤。水锤会造成压力管道及设备的振动，从而对管道及相关设施产生破坏，容易发生泄漏、火灾等安全事故。

关于轴流式止回阀防水锤方面的研究，主要采用公式、一维CFD 软件模拟等手段依据特征线法计算管道的瞬变流［1-4］。李小周等［5］依据瞬变流理论，采用特征线方法，计算了事故停泵对输水系统的危害，对比分析了两阶段液控关闭止回阀等系统元件联合防护措施的水锤防护效果。陈亚飞等［6］采用试验方法和数值计算分析关阀速度对水锤冲击波形的影响，基于经典水锤方程和特征线法，建立了一套快速分析关阀瞬态性能和水锤冲击效应的数值计算方法。关于阀门动态特性方面的研究，SONG 等［7］采用CFX 三维动网格技术模拟了系统从阀门开启到阀门关闭的完整瞬态过程，研究了直动式安全阀的流体动力学特性。ZANG 等［8］以核电站二回路中的主蒸汽阀站作为研究对象，利用动态网格技术模拟了不同入口直径的先导阀动态特性，同时分析了先导阀开启过程中的压力。SAHA 等［9］利用动网格方法研究了调压截止阀内部可压缩流的动态特性，同时研究了阀芯和阀体之间的摩擦系数与阀芯稳定性的关系，保证了调压截止阀出口压力的恒定。基于特征线法的一维CFD 数值模拟，无法体现流体压力、速度在三维空间中分布的不均匀性，导致计算精度较差，无法与实际效果符合。同时，轴流式止回阀的关闭过程是一个快速的动态过程，仅仅分析其稳态过流特性无法反映动态关闭过程中阀内流场的急剧变化以及阀芯的瞬态受力情况。

本文利用三维FLUENT 动网格方法对两种不同型号（优化前、后）的阀门内部动态流场进行瞬态模拟分析，探究阀瓣的实时运动状态，分析其动态特性曲线。比较两种型号的动态性能曲线，提高轴流式止回阀防水锤的能力，为实际工程设计提供一定的参考。

1 轴流式止回阀的结构及原理

轴流式止回阀结构如图1 所示。

轴流式止回阀主要由阀体、阀座、阀瓣、阀杆和弹簧等部件组成，两种轴流式止回阀结构仅阀瓣形状存在差异，优化前、后的阀瓣对流面分别为球形面与锥形面。轴流式止回阀关闭时，阀瓣运动方向与来流方向相反，阀瓣与来流间互相产生阻力，有效减弱了水锤的影响。轴流式止回阀的关闭过程中，随着阀前介质流量和压力的减小，在弹簧作用力和介质背压作用下阀门关闭以阻止介质回流［10-11］。LNG 轴流式止回阀性能参数见表1。

表1 LNG 轴流式止回阀性能参数Tab.1 Performance parameters of LNG axial flow check valve

2 FLUENT 动网格方法及数学模型

2.1 动网格方法

在流体工程应用中，常常需要获得边界变形或运动引起的瞬态流场变化信息，以真实地反映出流体机械的实时工作状况，比如泵、阀的启闭过程，压缩机中活塞的往复运动过程等都具有强烈的非定常特性。采用动网格方法研究流体机械的动态特性，以达到提高流体机械设计、使用性能的目的。动网格方法因其变形方式灵活、运动方式多样，在流体机械模拟中具有广泛的适用性。动网格数值模拟具有计算量大、计算周期长等特点，因而需要避免因小错误而导致反复计算造成计算资源以及时间的浪费。针对上述问题，前处理阶段需要仔细检查模型简化、网格划分、边界条件设置等相关步骤。利用动网格中的Zone Motion、Mesh Motion 模块分别预览边界运动、网格运动的状态，衡量计算的可行性，减少仿真模拟时计算资源及时间的浪费［12-13］。

2.2 湍流模型

在阀门内流场相关研究中，SST k-ω模型和RNG k-ε 模型的应用较为广泛［14］。大量关于止回阀的数值模拟文献中用试验证明了RNG k-ε模型的模拟精度［15-16］，因而模拟过程中选用RNG k-ε 湍流模型，其控制方程为：

式中，µt为湍流黏度，Pa·s；σk为与湍流动能k 对应的Prandtl 数；Gk为平均速度梯度引起的湍流动能k 的产生项；Gb为浮力引起的湍流动能k 的产生项；C1ε，C2ε，C3ε为经验常数。

2.3 阀瓣动力学模型建立

根据LNG 轴流式止回阀工作原理对阀瓣运动状态及受力进行分析。轴流式止回阀的流道模型简单且属于对称结构，因其主要的运动方向在水平方向，故不考虑其在竖直方向所受重力的影响。在水平方向阀瓣主要受到介质压力和弹簧力的作用［15］，摩擦力对轴流式止回阀整个过程影响较小可以忽略不计算。根据牛顿第二定律推导阀瓣运动方程为：

式中，m 为阀瓣的质量，kg；F1为液体压力，N；F2为弹簧力，N。

3 动态流场模拟研究

3.1 三维流域模型建立

LNG 轴流式止回阀全开工况下的三维实体模型采用SolidWorks 软件建立，反向建模生成与之对应的三维流道模型，其流域模型如图2 所示。流域模型及网格模型仅展示锥形阀瓣结构的，球形阀瓣结构依据同样的方法处理。

图2 轴流式止回阀流道模型Fig.2 Flow channel model of axial flow check valve

3.2 网格划分

在数值模拟过程中，鉴于Dynamic mesh 模块中网格更新方法对流域模型的要求，止回阀处于全开状态时，阀瓣与导向套之间至少需要一层网格，因而全开状态时的阀门开度为96%；同理，止回阀在关闭时同样不能实现完全关闭，认为阀门开度达到4%就实现了关闭。止回阀流体域网格划分如图3 所示。

图3 轴流式止回阀流道网格模型Fig.3 Flow mesh model of axial flow check valve

止回阀内部流域网格划分时，模型简单的前后直管段流域采用六面体网格，在保证计算精度的同时也减少计算资源的浪费；在流域复杂的区域，采用四面体网格更准确地实现该模型的包络，实现在压力梯度、速度梯度变化剧烈区域的高精度流场信息捕捉。为提高计算精度，阀瓣的流体域边界需划分高质量的网格以求解下一瞬时动网格流体域的边界形状，因此对阀瓣周围的流域进行加密处理。

3.3 网格无关性与时间独立性验证

在数值模拟过程中，网格无关性与时间独立性是消除计算结果随机性、保证计算结果准确性的必要手段。阀门全开工况下的流量系数是流场模拟中的重要参数值，可以作为网格无关性验证的标准。

图4 示出两种结构的轴流式止回阀全开工况下流量系数随网格数量的变化曲线。

图4 网格无关性验证Fig.4 Grid independence verification

网格数量相对较少时，流量系数的变化幅度很大；当网格数量达到150 万左右后，随着网格数量的增加，两种结构模型模拟得到的流量系数均趋于稳定。综合考虑计算资源与模拟精度，认为本次模拟在网格数量达到150 万后即满足网格无关性要求。

采用经过网格无关性验证的网格模型进行时间步独立性验证。分别选取0.005，0.001，0.000 5，0.000 1 s 4 组时间步长进行模拟试验，比较4 组时间步长下的止回阀开度随着阀瓣运动时间变化的曲线，优化前结构的模拟结果如图5 所示。

图5 时间独立性验证-优化前结构Fig.5 Time independence verification-structure before optimization

当时间步长为0.005 s 时，模拟得到的关闭时间相较于其他3 组值的偏差达到了8.5%，模拟精度相对较差无法满足时间步独立性要求。其他3组模拟得到的关闭时间偏差最大不超过2%，均满足时间步独立性的要求。优化后结构的模拟结果如图6 所示，同样在时间步长为0.001s 时满足时间步独立性要求。综合考虑模拟计算时间与精度等因素，选择时间步长为0.001 s 进行轴流式止回阀动态流场的模拟。

图6 时间独立性验证-优化后结构Fig.6 Time independence verification-structure after optimization

3.4 计算方法和边界条件

数值模拟中选用3D 双精度求解器，湍流模型运用SST k-ω模型，对流项的离散采用二阶迎风格式，扩散项的离散采用具有二阶精度的中心差分格式，速度和压力的耦合采用SIMPLE 算法。根据表1 完成介质属性的相关设置。运用动网格方法进行模拟计算时，选用Smoothing 和Remeshing两种网格更新方法模拟网格变形。轴流式止回阀属于自力式阀门，阀瓣的运动方式为被动运动，需要相应的UDF 编程计算阀瓣的运动状态。利用DFINFE_CG_MOTION 宏函数提取阀瓣的运动参数，同时阀瓣上受到的弹簧力和液体力也无法在软件中直接设置，需要编写相应的UDF，最后将UDF 进行并行化处理，以提高模拟计算的速度。阀瓣的运动分析流程如图7 所示。

同时，流场初始化对于数值模拟计算的收敛性及结果可靠性很重要，因而将稳态计算结果作为瞬态计算的初始场。利用UDF 设置入口流量随着时间减小，入口初始参考压力设置为0.1 MPa，出口设置为自由出流。鉴于止回阀的工作压力为4 MPa，即设置参考操作压力为4 MPa。

4 数值模拟结果分析

4.1 动态流场分析

阀瓣开始动作瞬间对应的止回阀开度为96%，对应阀瓣的运动时间为0 s；阀瓣关闭瞬间对应的止回阀开度为4%，对应优化前、后阀瓣的运动时间分别为0.09，0.107 s。鉴于轴流式止回阀具有很好的对称性，分别将优化前、后的压力、速度云图各取一半进行对比分析，优化前的云图位于上方，优化后的云图位于下方。

图8 示出轴流式止回阀优化前、后阀瓣开始动作瞬间及关闭瞬间的压力分布云图。

图8 优化前、后止回阀关闭过程压力分布对比Fig.8 Comparison of pressure distribution of the check valve in the closing process before and after optimization

阀瓣开始动作瞬间表明阀前压力不足以克服阀后压力和弹簧力的作用，受力平衡被打破。阀前、阀后管道内压力场分布比较均匀，轴流式止回阀内部压降主要发生在阀瓣位置，压力梯度最大。由于轴流式止回阀的对称性结构，周向流场的分布规律及数值是相同的。止回阀开度为96%时，优化前阀瓣顶端的高压区相比优化后更加明显，局部压力更是达到了100 kPa，阀瓣后流域的压力场分布基本相同。止回阀开度为4%时，认为阀门已经关闭，高压区集中在阀前管道，优化后阀瓣背面的压力分布相比于优化前压力梯度更小，更有利于降低止回阀运动造成的压力波动。

图9 示出轴流式止回阀优化前、后阀瓣开始动作瞬间及关闭瞬间的速度分布云图。轴流式止回阀节流主要发生在阀座形成的最小缩颈处以及阀体间最小的过流断面处，缓冲腔内形成了死区，流速最小。止回阀开度为96%时，速度最大值高达12 m/s，发生在阀座形成的最小缩颈处。止回阀开度为4%时，速度最大值高达13.7 m/s，发生在阀体与阀瓣形成的最小过流断面处，阀瓣优化后的流场最大速度小于优化前。

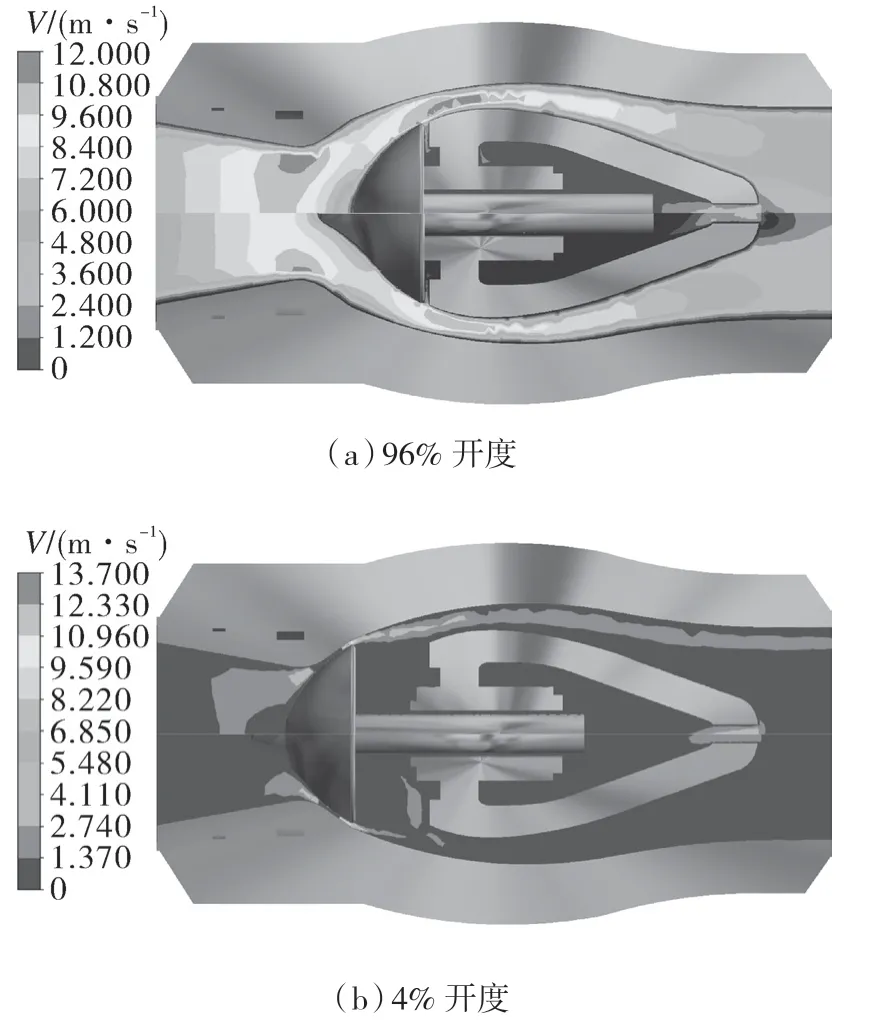
图9 优化前、后止回阀关闭过程速度分布对比Fig.9 Comparison of velocity distribution of the check valve in the closing process before and after optimization

4.2 关闭过程动态特性分析

图10 示出优化前、后阀瓣的关闭速度，阀瓣的运动速度随着运动时间的变化逐渐增大，增长达到拐点后，速度经过一段时间的缓慢下降后突变为0 m/s，优化前、后轴流式止回阀均具有“快关缓闭”的特征。优化前阀瓣的速度在运动时间为0.069 s 时达到最大值4.067 m/s，在运动时间为0.09 s 速度突变为0；优化后阀瓣的速度在运动时间为0.083 s 时达到最大值3.393 m/s，速度在时间为0.09 s 时突变为0。优化前阀瓣的最大关闭速度较优化后更大、关闭时间更短。

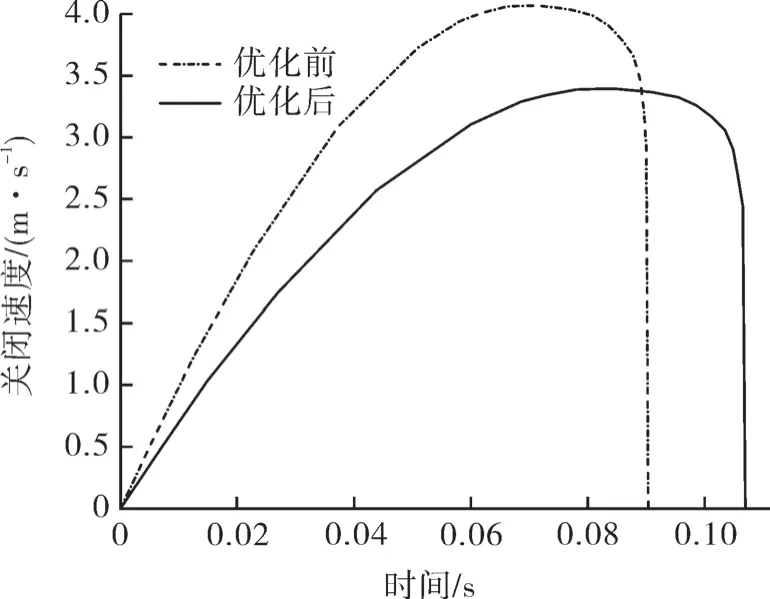
图10 优化前、后阀瓣的关闭速度Fig.10 Valve disc closing speed before and after optimization

图11 示出优化前、后阀瓣关闭过程中所受合力图，优化前、后的受力曲线均呈现波动性，同时阀瓣所受合力随时间变化的大体趋势具有一致性，达到拐点前，曲线伴随着波动呈线性下降趋势；经过拐点后，则在某一定值附近波动。优化后阀瓣受力曲线的波动幅度相较优化前更小。阀瓣开始动作瞬间受到的合力最大，优化前、后的合力值均在371 N 左右。当止回阀实现关闭时，优化前、后阀瓣所受合力值分别稳定在271，200 N。止回阀在关闭状态时，优化后阀瓣所受合力较优化前有所减小。

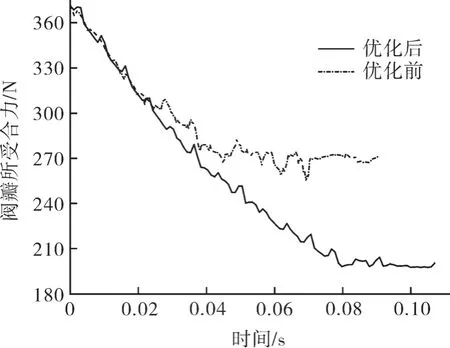
图11 优化前、后阀瓣所受合力Fig.11 The force of the valve disc before and after optimization

根据图8，9 中止回阀关闭过程流场分布对比对结构优化前后的阀瓣受力、阀瓣运动速度差异进行分析。在止回阀开度为96%时，流体即将流至球形阀瓣之前，有大范围的高压流体聚集，缩径处也有大范围高速流体，流体经过阀瓣后速度仍保持高速流动。而流线型锥形阀瓣前的高压、高速流体区域较小，且高压只存在于锥形阀瓣表面局部区域，最大压力较球形阀瓣表面更小，高速流体在壁面附近速度也较低。如图10 所示，球形阀瓣的关闭加速度明显大于锥形阀瓣，说明高压高速流体的范围大小决定了止回阀大开度时的关闭速度。在止回阀开度为4%时，高压区域聚集在阀瓣前表面，优化前、后阀瓣前表面所受压力基本一致，经过球形阀瓣表面的流体在主密封区域形成了高速流体，导致球形阀瓣前、后压差较大；锥形阀瓣后表面所受压力较前表面更小，因而在锥形阀瓣表面形成的压降更小，对应图11 中阀瓣受力的合力曲线较为平缓的部分。

将止回阀关闭过程中阀瓣所受合力经傅里叶变换后，得到相应的0～500 Hz 范围内的频域图。图12 示出优化前、后阀瓣所受合力的频域分析，优化前、后振幅随着频率的变化趋势大致相同，振幅峰值均出现在20 Hz 以内，峰值点分别为293，254N。在20～160 Hz 的频率范围内，振幅均在20 N 以下；在100～500 Hz 的频率范围内，振幅在0.1～2.0 N 之间波动，并且优化后的阀瓣振幅较优化前更小。

图12 优化前、后阀瓣受力频域Fig.12 Frequency domain of valve disc force before and after optimization

5 结论

（1）轴流式止回阀关闭瞬间，阀瓣受力由优化前的271 N 降低到200 N，证明锥形阀瓣对阀座的冲击力相较于球形阀瓣更小，因而在系统的防水锤的过程中对管道造成的振动更小。分析优化前、后阀瓣受力的频域图，发现该轴流式止回阀的阀瓣在20 Hz 以下频率内振幅出现了峰值，证明止回阀关闭过程中阀瓣的振动频率集中在低频区。

（2）对比优化前、后的阀瓣运动速度，优化后的阀瓣速度最大值相对较小，阀门关闭时对阀座的冲击速度较小，有利于提高阀座的使用寿命。

（3）利用动网格模拟方法对轴流式止回阀关闭过程的模拟能够得到阀瓣的运动状态以及阀瓣运动过程中的动态流场信息，对轴流式止回阀的设计及选型具有重要的参考价值。