基于有效牵引力系数的水力振荡器减阻效果评价方法

王学迎,张淙胜,张 恒,张菲菲

(1.长江大学 石油工程学院 油气钻完井技术国家工程研究中心长江大学分实验室,湖北 武汉 430100; 2.长江大学 油气钻采工程湖北省重点实验室,湖北 武汉 430100; 3.中国石油集团工程技术研究院有限公司,北京 102206)

引言

水平井是经济高效开发页岩油气、深海和深地等非常规油气资源的主要手段,目前陆地水平井仍主要采用弯螺杆导向钻具组合进行钻进,虽然其具有成本优势,但滑动钻进时摩阻大,导致机械钻速慢、工具面控制困难等问题,水力振荡器可以有效缓解上述滑动钻进难题[1-3]。

当前对水力振荡器的研究主要集中在工具研制方面[4-8],对安放位置、振荡短节选配和对井型的适应性等问题研究较少,进而导致水力振荡器的应用效果不稳定。国内外学者研究了水力振荡器的最佳安放位置,提出了一些评价标准,例如摩阻与振荡力的关系[9-14]、振动传播距离[15]和钻压平滑性[16]等,但这些研究或忽略了钻柱向前运动的影响,即边界条件假设不合理,或评价标准过于繁琐,难以应用。

考虑钻柱的动态运动,本文提出用有效牵引力系数来评价水力振荡器的应用效果,并依此指标研究机械钻速(Rate of Penetration,ROP)、水力振荡器碟簧组刚度和安放位置等因素对减摩阻效果的影响。

1 钻柱轴向振动传播模型

钻柱的轴向振动会引起横向的关联运动,但已有研究表明横向运动较弱,因此可将钻柱轴向振动问题简化为一维弹性波传播问题[17]。如图1所示,将钻柱系统离散为弹簧-质量模型,在该模型中钻柱的质量和弹性分别用刚体质量单元和拉压弹簧表示。

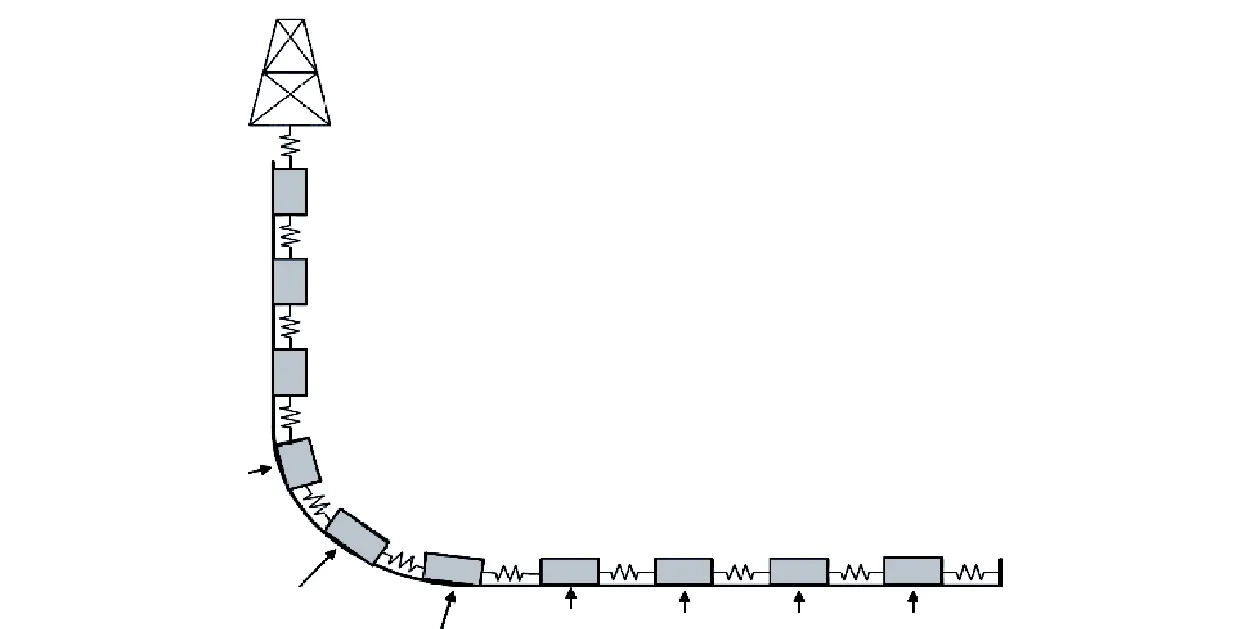
图1 钻柱系统的有限刚体模型[18]

相邻质量单元i和i+1(i=1,2,3,…,n)之间的弹簧刚度计算式为[17]

(1)

式中:k为等效刚度,N/m;L为钻柱单元长度,m;E为钻柱的弹性模量,GPa;A为钻柱单元的截面积,m2。

如图2所示,对任意钻柱单元i进行受力分析,可得

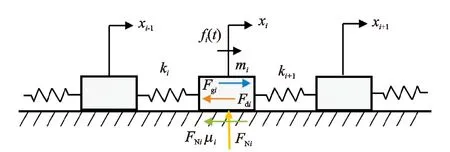
图2 钻柱单元受力示意图[18]

(2)

式中:x为轴向位移,m;m为钻柱单元质量,kg;Fg为重力在轴向的分量,N;FN为钻柱与井壁之间的接触正压力,N;μ为钻柱与井壁之间的摩擦系数;Fd为钻井液阻尼力,N;f(t)为激振力,N,假设水力振荡器产生的激振力符合正弦函数,对于非水力振荡器单元该值取零。

钻井液阻尼力可根据解析公式[18]近似估算,钻柱与井壁之间的接触正压力FN由软模型[18]计算,即

FN={[FtΔφsin(α-Δα/2)]2+[FtΔα+Wsin(α-Δα/2)]}1/2。

(3)

式中:Ft为钻柱轴向力,N;α为井斜角,rad;φ为方位角,rad;Δα和Δφ分别为测段内井斜角和方位角的变化,rad;W为钻柱单元的浮重,N。

对于钻柱轴向振动问题,存在两个边界条件,即地面边界和井底钻头边界。对地面边界,模拟司钻送钻过程,设置地面名义钻压为定值,即地面端轴向力为定值:

k1(x2-x1)=Fs(t) 。

(4)

式中:Fs为地面端轴向力,N,Fs短时间内保持为定值。

钻头处设置为速度边界,即给定钻头一个钻进的速度,该速度值与实际井底钻压成正比:

(5)

式中:Cp为钻速系数,m/s/N;WB为井底钻压,N;M为门限钻压,N。

使用中心差分方法求解方程(2)、(4)和(5)组成的轴向振动传播模型,可以获得模拟滑动钻进过程中钻柱各节点位移、速度随时间的变化情况,并可进一步分析井底钻压变化情况。

2 有效牵引力系数的定义

基于前述轴向振动传播模型开展数值模拟,得到井底钻压曲线,如图3所示。主要模拟参数:钻压72.5 kN,套管和裸眼段摩擦系数分别为0.25和0.35,钻井液密度1 200 kg/m3,钻井液排量30 L/s,黏度24 mPa·s,屈服值6 Pa,技术套管下深1 900 m,钻头深度3 470 m。钻具组合简化为127 mm钻杆1 410 m+127 mm加重钻杆530 m+127 mm钻杆1 530 m。水力振荡器激振力幅值10 kN,频率15 Hz。

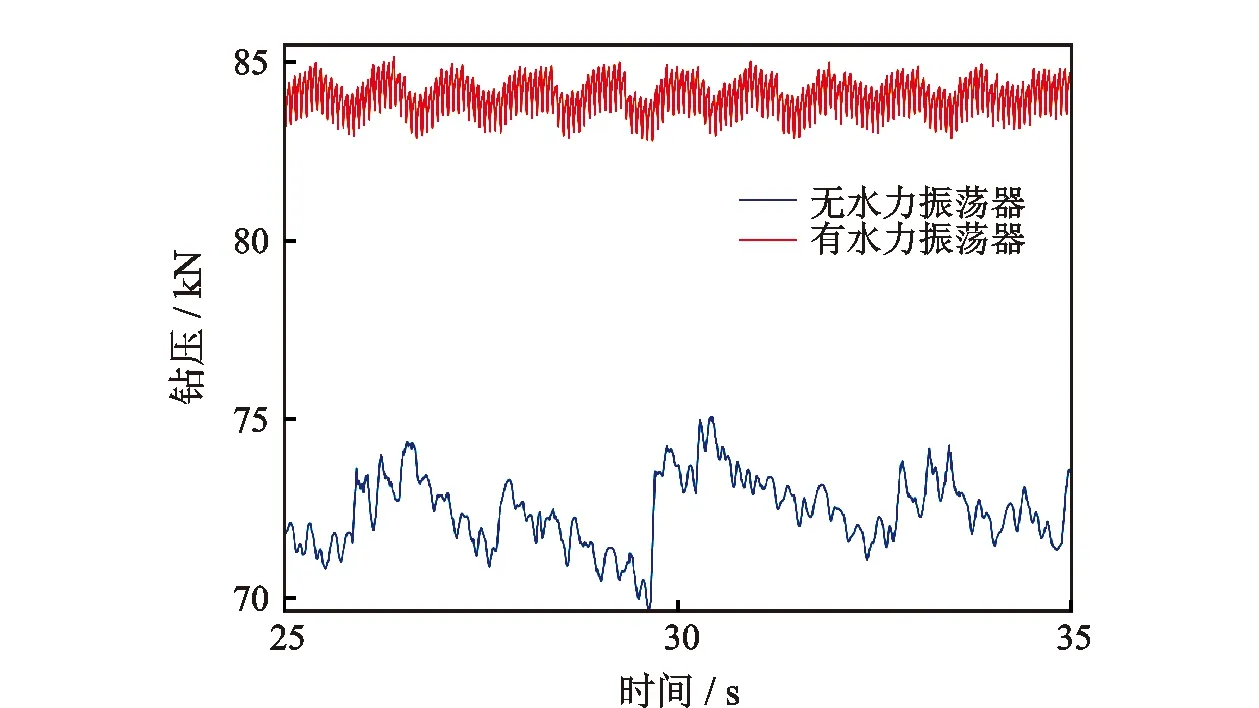
图3 水力振荡器增加井底钻压示意图

图3中,钻压曲线的频率反映了有无水力振荡器的情况下,钻柱系统轴向运动的基础频率和水力振荡器激励频率[19]。水力振荡器等轴向振动工具的使用会增加井底钻压,相当于在井底增加了一个向前的牵引力[9,15],该牵引力大小不仅与摩擦环境、激振参数有关,还与钻柱前进的速度有关。综合考虑上述因素,定义有效牵引力系数

(6)

式中:CETF为有效牵引力系数,无因次;WBb为基准钻压,即没有使用水力振荡器时的钻压平均值,N;WBe为同等工况下应用水力振荡器后的钻压平均值,N;Fe为水力振荡器的激振力幅值,N。

上述WBb和WBe都是在真实滑动钻进,即钻头向前运动的前提下获得的,而Wicks等[15]定义的有效牵引力并没有考虑钻柱的前进运动,导致水力振荡器的作用效果被放大。显然,当固定地面端轴向力时,有效牵引力系数越大,表明水力振荡器产生的减摩阻效果越显著,因此可用该系数来衡量水力振荡器的减摩阻效果。

3 有效牵引力系数的影响因素

影响水力振荡器减摩阻效果的因素很多,既包括水力振荡器自身的参数,如激振力幅值、激振频率和碟簧组刚度等,也包括摩擦系数、地层特性和安放位置等因素,本文以有效牵引力系数为评价指标研究这些因素对减摩阻效果的影响规律。

选择某二维定向井为例进行研究,其垂直剖面如图4所示。钻具组合简化为:215.9 mm钻头+127 mm加重钻杆8根+127 mm钻杆31根+水力振荡器+127 mm钻杆180根+127 mm加重钻杆12根+127 mm钻杆到井口。其他参数:钻压65 kN,钻井液密度1 200 kg/m3,钻井液排量30 L/s,黏度24 mPa·s,屈服值6 Pa,技术套管下深1 200 m,钻头深度3 470 m。采用控制变量法开展模拟,默认参数设置为:激振力幅值25 kN,频率20 Hz,碟簧组刚度4×107N/m,机械钻速3 m/h,套管段摩擦系数0.25,裸眼段摩擦系数0.35。

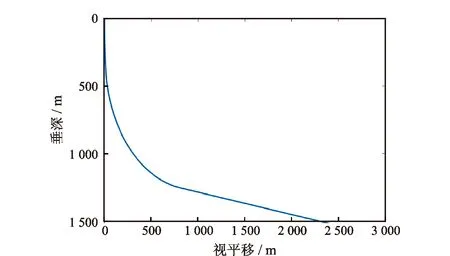
图4 某二维定向井的垂直剖面图

3.1 机械钻速和摩擦系数的影响

有效牵引力系数随机械钻速的变化如图5所示。由图5可以看出,有效牵引力系数随着机械钻速的增大而减小,机械钻速为零时有效牵引力系数取最大值,该最大值约等于2。水力振荡器有效牵引力的产生原理:没有水力振荡器时,钻柱单元向前运动,其所受的摩擦力向后,表现为阻力;存在水力振荡器的情况下, 某些原本只能向前运动的单元变为前后往复运动,当钻柱单元向后运动时,其所受的摩擦力向前,表现为牵引力,从而使得井底钻压增加。机械钻速增加时,振动难以使钻柱单元改变运动方向,即将摩擦力转化为牵引力越困难,因此随着机械钻速增加,有效牵引力系数逐渐减小。

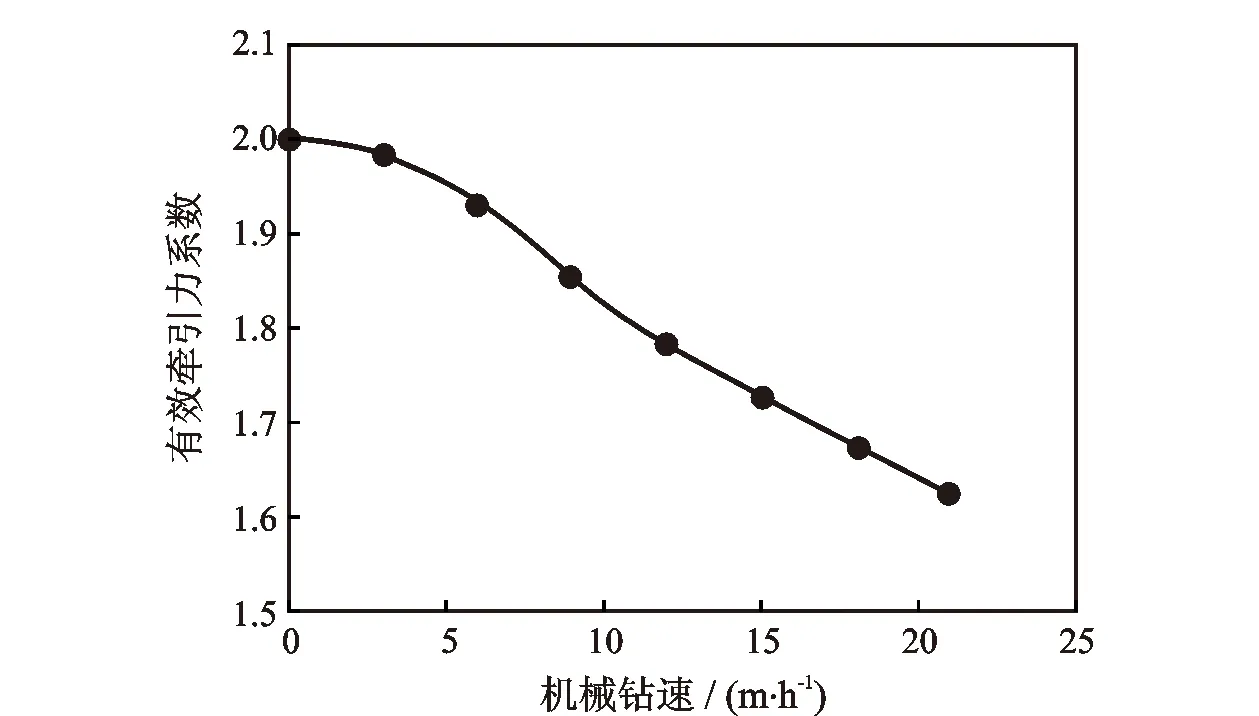
图5 有效牵引力系数随机械钻速的变化

激振力幅值分别为15 kN和25 kN时有效牵引力系数随摩擦系数的变化规律,如图6所示。为简化计算,在该部分模拟中令套管段和裸眼段的摩擦系数相等。由图6可以看出,当激振力幅值为15 kN时有效牵引力系数基本保持稳定,而25 kN激振力对应的有效牵引力系数先增加后保持稳定,原因是摩擦系数较小时(取0.20),钻柱所受摩阻值较小,相对激振力幅值而言没有足够多的摩擦力可被转化为牵引力,当摩阻值足够大时,有效牵引力系数基本不受摩擦系数影响。

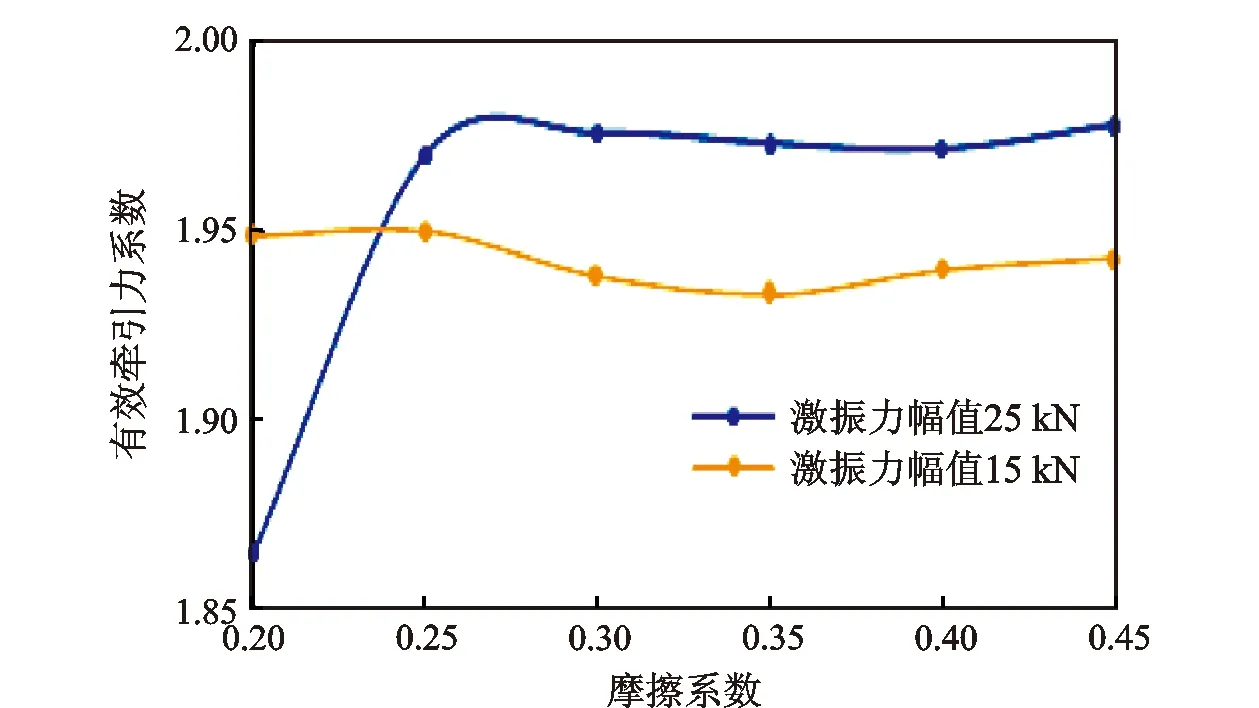
图6 有效牵引力系数随摩擦系数的变化

3.2 水力振荡器自身参数的影响

水力振荡器自身参数主要包括激振力幅值、激振频率和振荡短节的碟簧组刚度。一般而言,激振力幅值和激振频率并不是独立的,本文假设两者独立。有效牵引力系数随激振力幅值、激振频率及碟簧组刚度的变化规律,如图7—图9所示。

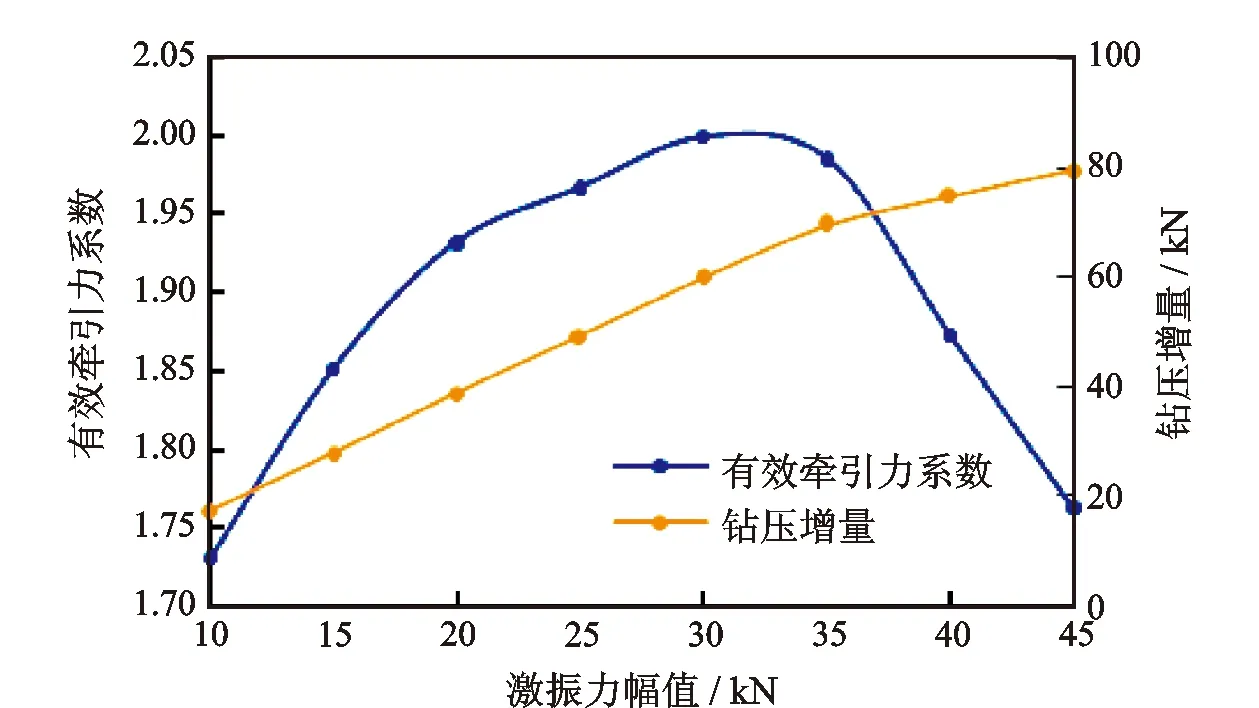
图7 有效牵引力系数和钻压增量随激振力幅值的变化

从图7中可以看出,对该算例而言有效牵引力系数先增大后减小,在激振力幅值小于30 kN时,增大激振力幅值,有效牵引力系数增大,即输入能量和能量利用率同时提高;当激振力幅值超过30 kN时,继续增大激振力,虽然井底钻压仍在增加,但有效牵引力系数逐渐下降,表明能量利用率下降。

从图8中可以看出,在15～25 Hz(大部分水力振荡器的工作频率)范围内有效牵引力系数波动较小,基本保持稳定,说明水力振荡器的工作频率对减摩阻效果影响较小。

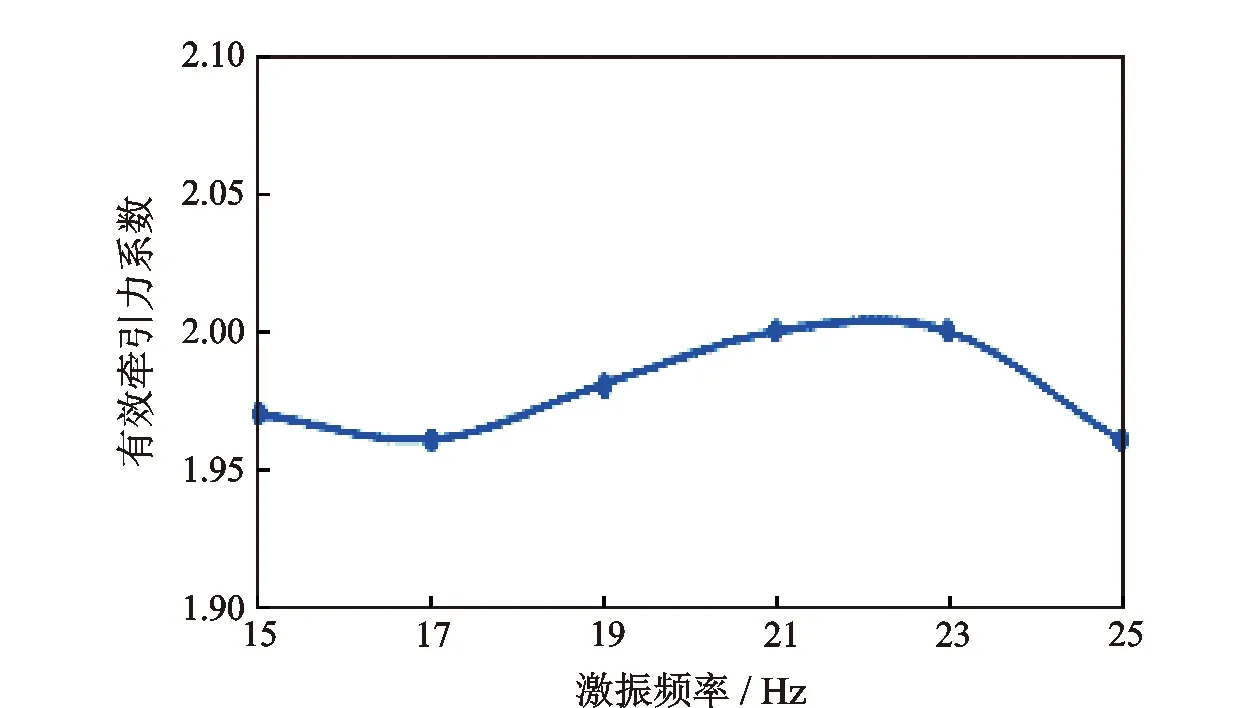
图8 有效牵引力系数随激振频率的变化

从图9中可以看出,碟簧组刚度对水力振荡器的减摩阻效果有较大影响,对给定工况存在最合适的碟簧组刚度,刚度太小或太大都不利于水力振荡器发挥效果。

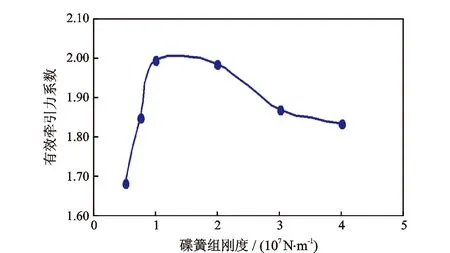
图9 有效牵引力系数随碟簧组刚度的变化

综上所述,激振力幅值和碟簧组刚度对水力振荡器的减摩阻效果有较大影响,而激振频率的影响较小,应根据实际摩阻大小选择相应规格的水力振荡器。

3.3 安放位置的影响

不同摩擦系数组合、不同机械钻速下,水力振荡器离钻头不同距离的有效牵引力系数变化如图10、图11所示。图例0.20-0.30表示套管段和裸眼段的摩擦系数分别为0.20和0.30。

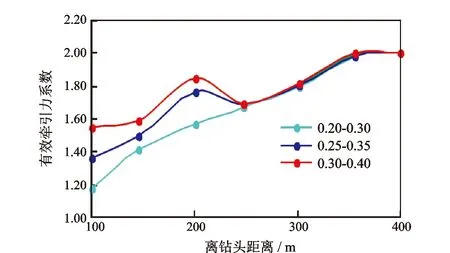
图10 不同摩擦系数组合下有效牵引力系数随安放位置的变化

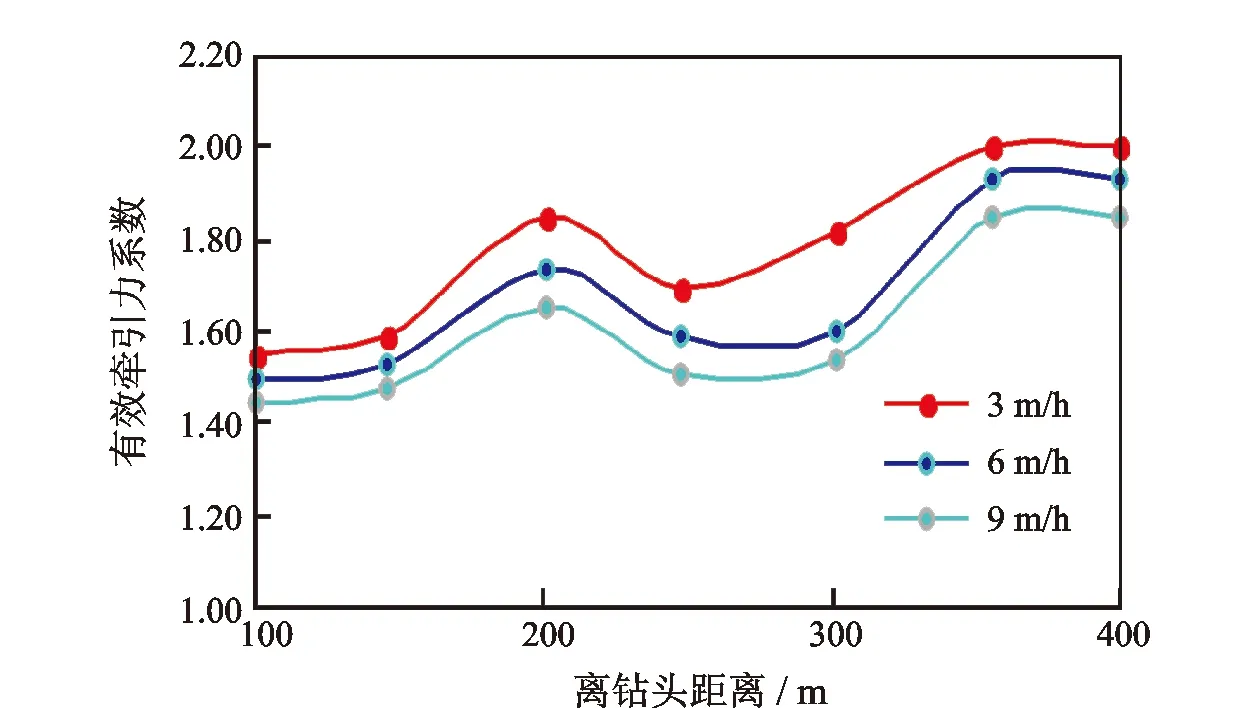
图11 不同机械钻速下有效牵引力系数随安放位置的变化

从图10中可以看出,有效牵引力系数随着离钻头距离的增加先增大后趋于平稳,安放位置在离钻头250 m以内时,摩擦系数越大对应的有效牵引力系数越大,原因是此时水力振荡器到钻头这段钻柱不能提供足够大的摩擦力来转化为牵引力,超过250 m后钻头到水力振荡器之间的摩擦力已足够大,有效牵引力系数不再受摩擦系数的影响。从图11中可以看出,3条曲线的变化趋势基本一致,即机械钻速不影响有效牵引力系数的变化规律,但随着机械钻速增加,有效牵引力系数逐渐减小。

在图10和图11中,尽管摩擦系数和机械钻速在变化,但安放位置距钻头200 m始终为一个极值点,这与弹性波的反射和传播有关。基于位移模拟结果发现,弹性波在钻柱中的传播速度为5 313 m/s(钢材弹性模量取206 GPa,密度取7 850 kg/m3,理论波速5 123 m/s,受碟簧组边界影响与理论值有所差别),激振频率为20 Hz时对应的波长为265.64 m,钻头到水力振荡器的距离为200 m时对应着0.75倍波长(模拟发现x.25或x.75倍波长具有同等效果,x=0,1,2,…)。由原始波和反射波的传播(图12)可知,此时反射波推动钻柱单元反向运动,增强了将摩擦力转化为牵引力的能力。

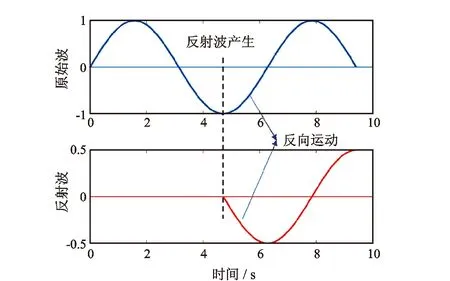
图12 轴向激励原始波和反射波传播示意图

综上所述,最佳的水力振荡器安放位置应该在有效牵引力系数达到平稳值的第一个点,即图10和图11中离钻头350 m的位置处。

4 现场应用案例

为验证有效牵引力系数评价方法的可靠性,在5口定向井中进行了应用。5口井中水力振荡器安放位置调整前后的机械钻速对比情况见表1。表1中的对比井为本井前后对比或相同井型的邻井对比,安放位置指水力振荡器离钻头的距离,井型中的角度值为本井最大井斜角。

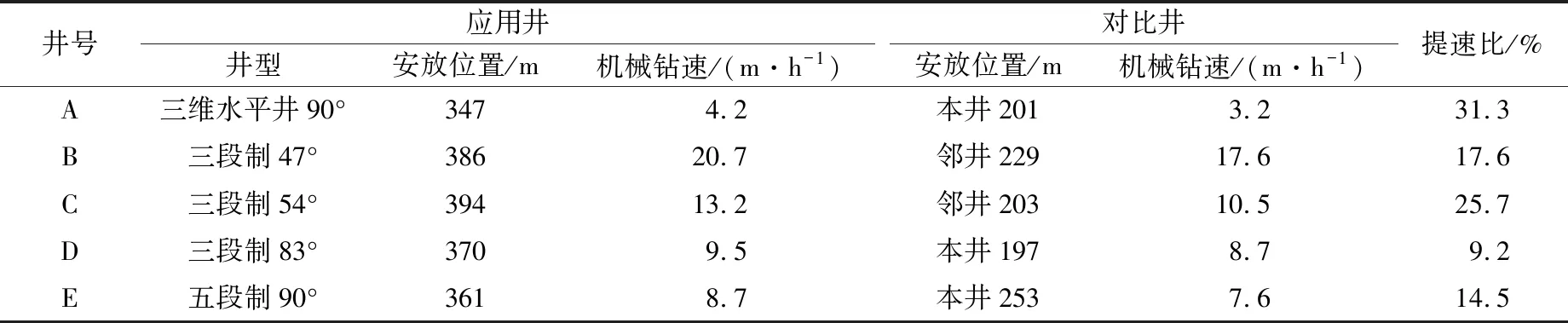
表1 水力振荡器安放位置调整前后的机械钻速对比情况

从表1可以看出,优化后水力振荡器离钻头的位置均有所增加,调整后的机械钻速增加明显,表明调整后减摩阻效果得到改善。以上对比结果说明,使用有效牵引力系数能够科学有效地确定水力振荡器的安放位置。

以井A为例进行详细说明。井A的垂直剖面图如图13所示,该井初始钻具组合为:Φ215.9 mm PDC+172 mm弯螺杆+回压阀+Φ127 mm 加重钻杆(2柱)+Φ127 mm 钻杆(S135、5柱)+Ⅱ型水力振荡器+127 mm钻杆(S135、89柱)+Φ127 mm厚壁钻杆(33柱)+Φ127 mm加重钻杆(S135)。其他参数:钻压60～90 kN,排量32 L/s,水力振荡器激振力幅值36 kN,频率19 Hz。

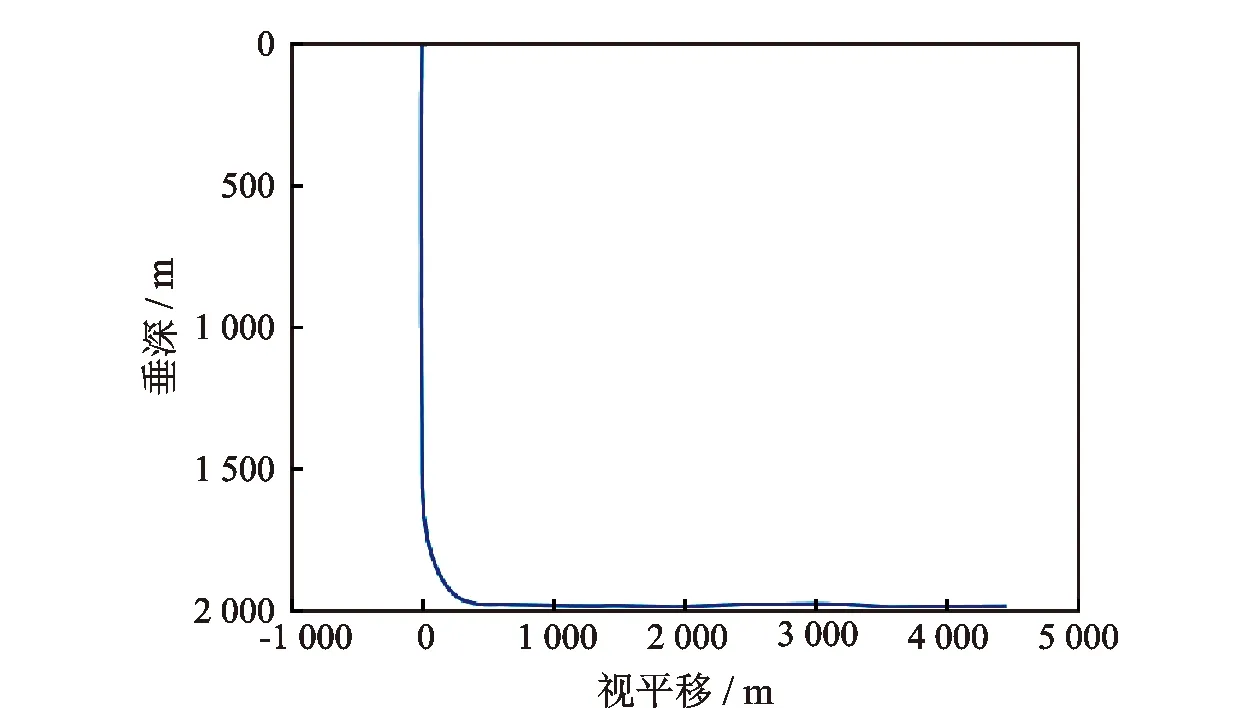
图13 案例井A井的垂直剖面图

由于水平段较长,该井滑动钻进至4 570 m时托压现象明显,表明此时水力振荡器的减摩阻效果较差。不同水力振荡器安放位置下的有效牵引力系数曲线如图14所示。根据图14,应该将水力振荡器安放在距钻头400 m位置处,考虑到近钻头位置处钻柱刚性较大且井眼轨迹不光滑,摩阻可能被低估,因此起钻后将水力振荡器的安放位置由钻头后201 m调整为347 m。调整后托压现象消失,定向工具面稳定,机械钻速由3.2 m/h提高到4.2 m/h。

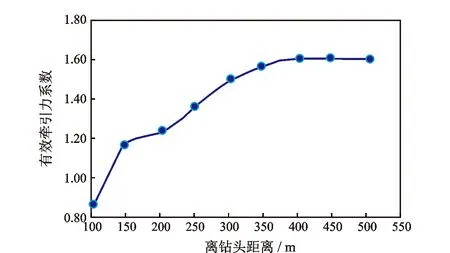
图14 案例井不同安放位置下的有效牵引力系数

5 结 论

(1)水力振荡器产生的有效牵引力随机械钻速增加而降低,对摩擦系数不敏感;

(2)激振力幅值和碟簧组刚度对减摩阻效果有较大影响,而激振频率的影响较小;

(3)有效牵引力系数随水力振荡器离钻头距离的增加先增大后趋于平稳,最佳的工具安放位置为有效牵引力系数达到平稳值的第一个点;

(4)现场应用结果证明,本文提出的基于有效牵引力系数方法评价水力振荡器的减摩阻效果和优化安放位置可行。