横向振动状态下水润滑轴承摩擦动力学特性∗

杨 俊 田佳彬 喻家鹏 张雪冰 何 涛 解忠良 杨 康

（1.武汉第二船舶设计研究所 湖北武汉 430205；2.西北工业大学工程力学系 陕西西安 710072）

工程中一直在寻找弊端明显的传统润滑方式的替 代形式，尤其是旋转机械的研发与设计领域。其中，轴承作为关键的支承承载部件，润滑方式的好坏决定了机构的性能优劣，更影响着传动系统的正常推进。而水润滑轴承具备的环保清洁、来源广泛、安全可靠的天然优势，完全可以避免油润滑方式的缺陷。此外，在海上以及深水工作的机械设备所需的支撑装置中，水润滑轴承具备独特优势。目前，水润滑轴承已经在诸多关键核心场合有了大量的应用，比如：高性能舰船推进系统［1］、核主泵系统、海上平台定位装置等。国内外学者已经从水润滑轴承的润滑性能［2］、动态行为［3］、多因素耦合特性［4］等方面开展了深入而广泛的研究，并取得了一系列积极成果。

在机械系统中，摩擦和振动是广泛存在且不可避免的，同时彼此之间相互作用［5］。一方面，摩擦力会引起预期之外的振动，比如悬臂效应下，水润滑艉轴承容易出现接触摩擦，诱导振动出现，出现恶劣的摩擦磨损行为，对推进轴系的稳定运转产生不确定因素。另一方面，在机械系统中加入振动，又可以极大地影响摩擦力。YAN 等［6］开展了超声波振动对复合材料摩擦学性能的影响，实验结果表明超声波振动显著降低了材料的摩擦力。近年来，水润滑轴承的摩擦学性能和轴系振动特性的研究备受关注，相关研究成果促进了水润滑轴承研究体系的完善。HAN 和LEE［7］研究了水润滑艉轴承黏滑非线性摩擦诱导振动机制，研究采用了两自由度模型描述了轴承系统，并根据轴承界面上的正常载荷、轴承阻尼、固有频率等系统参数进行了稳定性分析；同时利用一个能够模拟船舶推进轴的黏滑非线性摩擦诱导振动的测试单元，再现了黏滑非线性摩擦诱导振动。TIAN 等［8］研究了载荷、滑动速度、温度、水润滑等因素对复合材料摩擦行为和磨损机制的影响，研究结果表明，水润滑形式对复合材料的影响不如载荷效应和温度效应明显。ZHANG 等［9］对一种新型复合材料在水润滑摩擦作用下的振动行为展开研究，结果表明新型材料可将摩擦振动产生的机械能转换为热能，并减小了由摩擦产生的振动和噪声行为。CHEN 等［10］对水润滑轴承启动过程中的摩擦动力学行为进行了研究，探讨了轴颈的振幅对水润滑轴承启动过程中摩擦动力学行为的作用，分析了在表面粗糙度为径向间隙范围内对水润滑轴承摩擦动力行为的影响。YANG 等［11］开展了磨损对水润滑橡胶摩擦振动抑制行为的研究，探讨了有无表面纹理的橡胶板条的磨损对摩擦减振机构的影响，试验结果表明，表面纹理可以适应磨砂粉尘和储水功能，可以有效改善2 个摩擦面之间的湿态条件，降低摩擦因数，从而有助于提高水润滑橡胶板条轴承高频摩擦振动的抑制水平。HUANG 等［12］探讨了考虑黏滑行为的轴承系统的摩擦诱导振动的影响因素，分析了基于实验数据得到的黏结系数和滑移系数对摩擦因数的影响，得到了动摩擦因数、相对速度和反作用力的响应，对轴承系统的各种影响因子进行了稳定性分析。

综上，水润滑轴承的摩擦学性能研究已经取得了较大进展。但不同润滑阶段的振动影响摩擦力的完整机制尚存不足，相关研究并不清晰。推进系统在启停、转向、低速重载等特殊条件下，轴承的润滑状态大多处于边界润滑和混合润滑，此时极易出现边界摩擦甚至干摩擦。而且，推进轴系上存在多种类型的支承部件，有螺旋桨、多个中间轴承和船艉轴承在轴与船体之间传递横向振动，所以控制横向振动比控制纵向振动要复杂得多［13］。因此，本文作者开展了横向振动对水润滑轴承摩擦力影响的研究，构建了混合润滑和流体动压润滑状态下轴系的横向振动动态模型，分析并比较了2 种润滑状态下的振动特性；将轴颈稳态下的平衡位置代入轴承横向振动模型，得到了轴颈扰动量；通过水润滑轴承流体动压润滑程序计算了轴颈受到扰动后的轴承摩擦力。研究结果为评估横向振动对摩擦力的影响程度和揭示轴承摩擦振动机制提供基础。

1 理论分析

1.1 雷诺方程

图1 所示为水润滑轴承结构。当水润滑轴承工作在混合润滑状态时，水膜厚度与表面粗糙峰高度在同一量级，此时表面粗糙度将对水膜流场产生很大影响，在计算水膜压力时需要考虑主轴与轴承的表面粗糙度。对于水润滑滑动轴承等共形表面的混合润滑问题，一般采用PATIR 和CHENG 提出的平均流量模型：

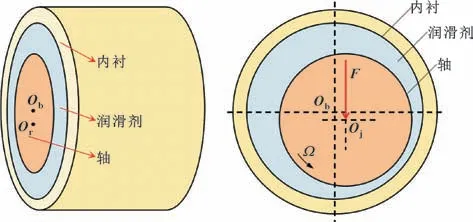
图1 水润滑轴承结构Fig.1 Structure of water lubricated bearing

式中：x、z为圆周方向和轴向方向；ϕx、ϕz为θ、z方向的压力流量因子；ϕs为剪切流量因子；σ为轴和轴承两表面综合粗糙峰度的标准差；h为名义膜厚（轴和轴承两表面粗糙度中线间的距离）；p为水膜压力；η为水的黏度；U为主轴外表面的线速度。为实际膜厚hT的平均值，即实际水膜厚度的数学期望。

对于径向滑动轴承，以θ为圆周方向角度，z为轴向方向，用极坐标表示其雷诺方程：

式中：R为轴承半径；ϕc为接触因子。

有关上述各类修正因子ϕθ、ϕz、ϕs和ϕc的计算方法可参照文献［14］。

1.2 膜厚方程

根据正弦定理可得膜厚沿周向的分布公式为

式中：c0为半径间隙；e为偏心距；ψ为偏位角；δ为弹性变形量。

弹性变形计算采用Winkler 法，控制方程为

式中：B为轴承内衬厚度；E为衬层弹性模量；ν为材料泊松比；pa为接触压力。

则膜厚比可表示［15］为

式中：hmin为最小名义厚度；σ为粗糙度标准差；σ1为转轴粗糙度；σ2为轴承内衬粗糙度。

当1≤λ≤3 时，认为轴承处于混合润滑状态。

1.3 微粗糙接触模型

图2 所示为水润滑轴承润滑状态示意图。当水润滑轴承工作在混合润滑状态时，主轴与轴承表面发生局部微凸体接触，产生固体接触压力，此时外载荷由水膜力和固体接触力共同承担。固体接触压力的计算采用Greenwood 微凸体接触模型［16］，该模型使用简单、计算效率高，模型假设了粗糙峰的高度呈指数分布且粗糙峰顶端为球形，其方程为

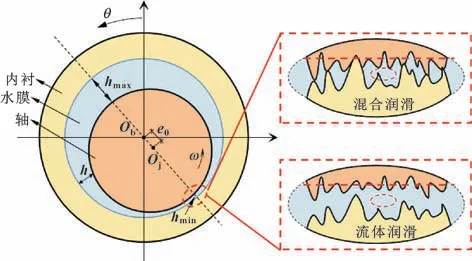
图2 水润滑轴承润滑状态Fig.2 Lubrication state of water－lubricated bearing

式中：β为粗糙峰密度；D为粗糙面曲率半径；F2.5为不同膜厚比的分布函数；E∗为复合弹性模量，计算方法见下式［17］：

式中：ν1、ν2为轴承和轴颈的泊松比；E1、E2分别为轴承和轴颈的弹性模量。

分布函数一般使用高斯积分计算，计算方法如下：

多项式分布法：

在实际计算中，为简化计算难度，一般采用多项式近似代替高斯分布，高斯分布与多项式分布曲线的对比如图3 所示，可以看出多项式分布与高斯分布相比较具有很好的近似性。

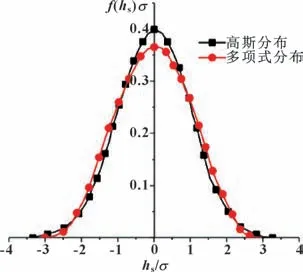
图3 多项式分布与高斯分布的分布概率对比Fig.3 Distribution probability comparison between polynomial distribution and Gaussian distribution

1.4 承载力方程

对于处于混合润滑状态的径向滑动轴承，外部载荷由润滑膜与微凸峰共同承担。其中润滑膜在水平和垂直方向的承载力可用下式求得：

微凸峰在水平和垂直方向的承载力可用下式求得：

式中：Fwx为水平水膜承载力；Fwy为垂直水膜承载力；Aw为完整水膜区；Faspx为水平接触承载力；Faspy为垂直接触承载力；Aasp为粗糙峰接触区。

当承载力与外载荷平衡时，有：

式中：W为外部载荷；Fw为流体动压力；Fasp为微凸峰接触力。

1.5 摩擦力

混合润滑轴承的摩擦力由流体剪切力形成的液膜摩擦力与微凸峰接触摩擦力两部分组成。流体在摩擦副界面处的平均剪应力为

式中：正号适用于摩擦面2，负号适用于摩擦面1；ϕf、ϕfs、ϕfps均为剪切应力因子。

由流体剪切力形成的液膜摩擦力可按下式求得：

微凸峰接触摩擦力可按下式求得：

总摩擦力为

摩擦因数为

1.6 横向振动轴承位移

如图4 所示，船舶艉轴系在启停和低速运行过程中，艉轴轴颈的受力情况主要为接触面间法向和切向的相互作用力、外加动载荷和自身重力。随着转速的降低，艉轴轴颈逐渐与轴承接触，接触面间的润滑形式从动压润滑转变为半干摩擦，法向力则从液膜支撑力为主体过渡到以轴承的弹性力为主体，切向力则从轴颈与液膜之间的流体摩擦转变为轴颈与轴承间的动摩擦。对于启动后的缓慢升速阶段，这个转变过程则相反。

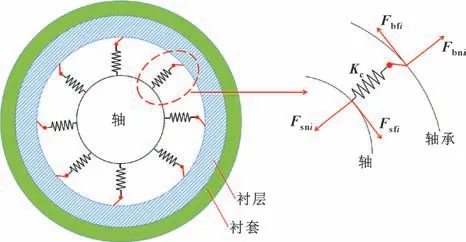
图4 摩擦振动模型Fig.4 Frictional vibration model

为了降低分析过程的复杂性，对上述的力学模型进行一定的简化。艉轴轴颈与轴承尚未接触的时候，其法向上的受力仅为单一的液膜支撑力，轴颈与轴承一旦接触，则液膜支撑力消失，法向力变为轴承的弹性支撑力Fn。由此，可以得出：

式中：x、y、、分别为轴颈中心的位移和速度量；Kb为轴承压缩刚度。

液膜支撑力是与位移、速度相关的非线性变化量，要通过雷诺方程进行简化求解，但目前研究的时间域在未接触到接触这个微小范围内，液膜逐渐破坏，其对横振影响较小。因此设定液膜力为支撑艉轴的一个静态力，在动态分析时予以忽略。令r＝，式（18）变为

式中：Cp设定为支撑轴颈的静态液膜力，动态分析时忽略；r为轴颈的径向运动位移。

艉轴轴颈与轴承尚未接触时，其切向上的受力仅为轴颈与流体之间的摩擦力，相对于其他受力，该摩擦力很小，基本可以忽略不计。当轴颈与轴承开始接触时，切向受力则视为动摩擦力。摩擦因数采用某个常数。

艉轴轴颈受到的外载荷主要来自于螺旋桨的流体激振力和艉轴的偏心载荷，低速时这些激励在振幅上起主要作用的是第一阶分量，高阶分量都可以忽略掉。

考虑偏心激励一种载荷，因此可以得出：

式中：e0为偏心距；ω为角速度。

通过简化假设在X、Y方向上系统是各向同性的，则阻尼刚度是相等的，由此建立讨论横向振动和摩擦相互耦合的运动方程。

式中：k为系统刚度；c为系统阻尼。

1.7 接触后模型的求解方法

令x1＝x′，x2＝，y1＝y′，y2＝，cosθ＝x／y，sinθ＝y／r，则可将式（22）的微分方程降阶为一阶方程组：

设定轴颈的初始位置为r＝0.05 mm，初始偏位角为60°，v＝1.89 m／s。

在实际降速过程中，轴颈与轴承发生表面接触是在一定范围的面上，为了简化数值分析，假设轴颈与轴承的接触是点接触，且发生接触时的角度为60°。将选择的各项参数代入到方程组中，以0.01 s 为间隔，求解2 s 内的位移响应曲线。

1.8 流程图

图5 所示为系统求解流程框图，针对不同工况分别在不同润滑模型中分析计算。在轴承流体完全动压润滑状态下横向振动建模方面，基于水润滑轴承流体动压润滑静动特性程序，获得稳态工况下的轴颈平衡位置与8 个水膜动特性参数。根据水膜动特性参数，推导线性化水膜力公式，引入外界激励，构建轴承横向振动模型。假设轴颈受到外界激励后，轴心轨迹为椭圆形，将轴颈稳态下的平衡位置代入轴承横向振动模型，可解得轴颈扰动量。最后，通过水润滑轴承流体动压润滑程序计算轴颈受到扰动后的轴承摩擦力。在轴承与轴颈接触状态下横向振动建模方面，通过将轴颈的运动位移加入动摩擦力的法向载荷描述，在横向振动与摩擦振动相结合的力学模型基础上建立了计入动摩擦力和外界激励的耦合振动方程，采用四阶龙格库塔法求解振动方程可得到轴颈的位移扰动量，将其输入水润滑轴承混合润滑程序即可得到轴承的摩擦力变化曲线。

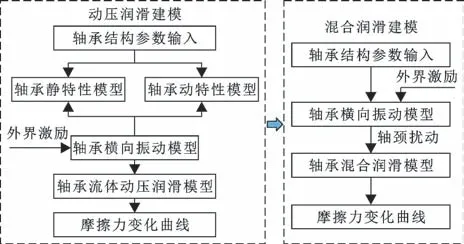
图5 系统求解流程Fig.5 The flow of system solution

1.9 模型验证

为了验证该模型的准确性，将文中求解结果与文献［18］的仿真结果进行对比。轴承和工况基本参数如表1 所示。

表1 轴承结构和工况参数Table 1 The structural and working parameters of the bearing

基于表1 中的参数，采用项目组已有的瞬态流体动压轴承计算程序，计算得到轴承润滑特性参数和动特性参数，分别与文献［18］中结果进行了比较，如表2 和表3 所示。

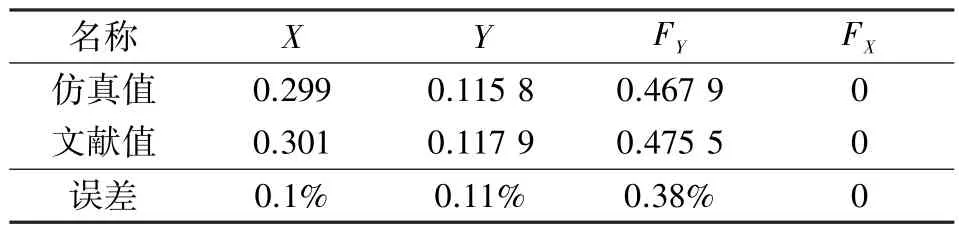
表2 轴颈量纲一平衡位置及承载能力对比Table 2 Comparison of journal balance position and loadbearing capacity

由表2 和表3 可知，润滑特性参数和动特性参数的相对误差均小于2%，验证了项目组现有瞬态流体动压润滑计算程序的准确性。

设置偏心激励幅值为0.1，对轴承受到偏心激励时的轴心轨迹进行模拟，结果如图6 所示。

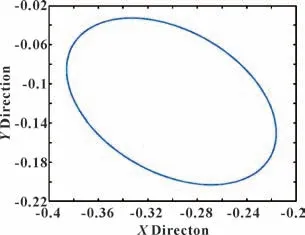
图6 偏心载荷为0.1 时的轴心轨迹Fig.6 Axis center trajectory at an eccentric load of 0.1

将文中模型得到的轴心轨迹的水平和垂直方向的变化幅值和文献［18］进行对比，如表4 所示，可知幅值相对误差均在1%以内，表明文中建立的横向振动模型较为可靠。

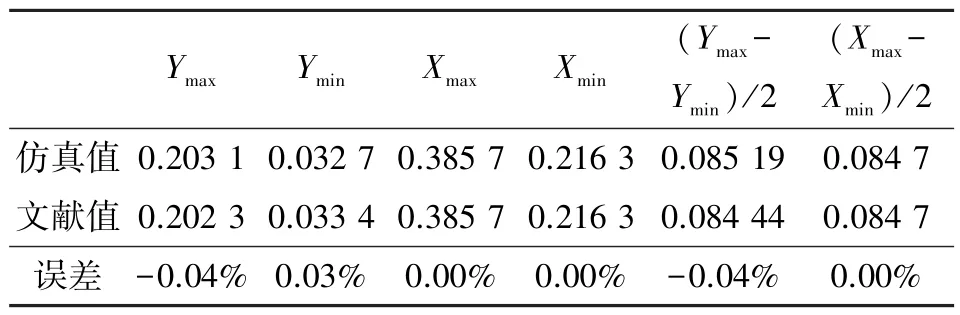
表4 振动幅值对比Table 4 Vibration amplitude comparison

2 结果与讨论

2.1 算例介绍

文中分析对象选择船舶轴系性能综合试验平台中的水润滑轴承，如图7 所示。试验平台主要由变频电机、减速器、推力轴承、轴系及附件、加载装置、水润滑单元与液压动力单元、监测控制单元、地基和机座组成。其机座安装于地基上，试验台轴系设备都安装在机座上。变频电机输出端接转速／扭矩传感器后连接在减速机上，减速机后通过高弹联轴器连接推力轴承，推力轴承后接轴系及附件。轴系包括2 根中间轴和1 根艉轴，中间轴和艉轴用液压联轴器连接，中间轴由中间轴承支撑，艉轴由2 个油润滑艉轴承组件或由1 个水润滑艉轴承和一个油润滑前艉轴承支撑。艉轴后端设置力加载装置和转矩加载装置，其中负荷加载装置包括轴向力加载和径向力加载，可以完成脉动载荷的加载。

图7 试验平台艉轴承示意Fig.7 Schematic of the stern bearing of the test platform

研究对象的结构如图8 所示，该艉轴承轴瓦由多个板条紧密楔合在一起，板条材料为有机高分子化合物，润滑介质为清水，水温30 ℃。轴承工作面为平面型，其基本尺寸参数与工况如表5 所示。

表5 轴承基本参数与工况Table 5 Basic parameters and working conditions of bearing

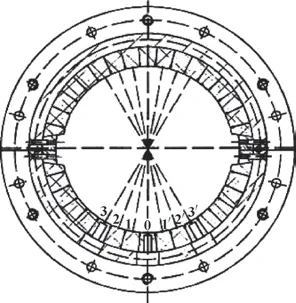
图8 轴承结构示意Fig.8 Schematic of bearing structure

2.2 参数选取

该台架艉轴颈等效质量m＝254.8 kg，动压润滑状态下外界载荷设置为轴颈自身重力，转速为5 00 r／min 以保证处于动压润滑状态。接触前，艉轴颈所受到的阻尼力主要是黏性流体介质的阻力，其阻尼系数与刚度系数由该工况下动特性模型求得。

当艉轴与轴承存在接触，根据以往试验结果选取混合润滑下转速196 r／min，该工况下外界载荷设置为轴颈自身重力。艉轴颈与艉轴承接触后的最大变形主要体现在轴承某一板条上的有机高分子材料层，参考文献中的橡胶层压缩刚度系数公式：k2＝E0A（1＋为第一形状系数，对于试验中的水润滑高分子材料艉轴承，其压缩模量E0＝8 088 MPa（SF－2），材料层长度a＝0.608 m，宽度b＝0.03 m，材料层厚度tr＝0.012 m。文中所研究的有机高分子材料艉轴承硬度偏高，因而硬度系数k选0.95。由此，可以得出材料层的压缩刚度Kb＝5.452×108N／m。

接触后，依据阻尼经验公式C＝0.023mω／N，在试验工况下集中载荷取值为：N＝5 624 N，在对应的转速下计算相应的C值。

艉轴颈与艉轴承接触后的系统刚度是液膜刚度、轴承刚度、接触刚度等的综合结果，采用一般中间轴承支撑的设置刚度5×109N／m。

由于船舶艉轴系的复杂工况，使得艉轴质量中心与几何中心产生不可忽视的偏心距，文中所讨论的耦合振动也必须考虑偏心距的影响。参考以前学者的设定值，选取静平衡时偏心距e0＝1 mm。

产生接触后的摩擦因数根据该轴承实验中的摩擦因数来选择，如表6 所示。

在实际降速的过程中，艉轴颈与艉轴承表面接触是在一定范围的面上，为了简化数值分析，假设轴颈与轴承的接触是点接触，且发生接触时的初始角度为60°。

2.3 完全流体润滑下横向振动对轴承摩擦力的影响

由于研究的为动压润滑状态下横向振动对轴承的影响，因此设置外界载荷为轴颈的等效质量254.8 kg，转速为500 r／min。

首先将轴承基本参数和工况参数输入至轴承润滑模型，求得稳态下轴颈量纲一平衡位置为（－0.400 7，－0.851 8），水膜合力为2 418.495 0 N，偏位角为25.191 6°。接下来，将稳态下的轴承静特性参数代入轴承动特性模型求解得到轴承的4 个刚度系数和4个阻尼系数，如表7 所示。

表7 稳态下轴承的量纲一径向动特性参数Table 7 Radial dynamic characteristic parameters of bearing under steady－state conditions

设置轴承偏心激励幅值为0.1，转速为500 r／min，计算横向振动下轴颈的轴心轨迹，结果如图9所示。轴颈的量纲一水平位移范围为－0.399 1～－0.410 3，相比轴心水平平衡位置的波动幅度比约为4.00%；量纲一垂直位移为－0.856 0～－0.847 6，相比轴心垂直平衡位置的波动幅度比约为4.93%。可以看出，在激励幅值为0.1 的偏心激励下，横向振动对轴心位置的影响较小。

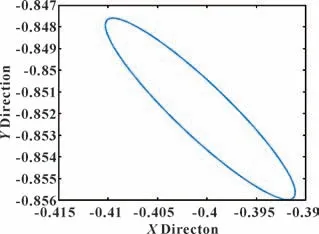
图9 轴心轨迹（εg＝0.1）Fig.9 Axis central trajectory（εg＝0.1）

轴承受到偏心激励后的水膜承载力的变化曲线如图10 所示，轴承的水膜承载力随着时间的变化呈正弦波动，最小水膜力为2 411.41 N，最大水膜力为2 475.94 N，载荷的波幅比为1.17%。相比平衡位置水膜承载力，横向振动后水膜的平均承载力有小幅增长，增幅为0.88%，表明受到激励幅值0.1 的偏心激励后，艉轴承能够承担外界载荷，水膜承载力波动较为稳定，不会造成轴承内衬的摩擦噪声、局部磨损等异常现象。

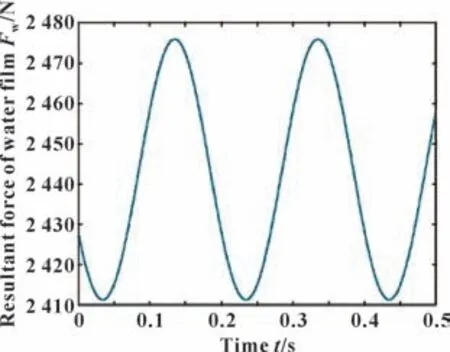
图10 水膜承载力波动曲线（εg＝0.1）Fig.10 The wave curve of water film bearing capacity（εg＝0.1）

为了研究振动程度对轴承摩擦力的影响，设置偏心激励幅值为0.1、0.2、0.3、0.4 和0.5，分析动压润滑下横向振动程度对轴承摩擦力的影响规律。轴承在平衡位置的水膜承载力为2 418.495 0 N，摩擦力为7.513 7 N。

以偏心激励幅值为0.3 的工况为例，轴承受到横向振动后的摩擦力变化曲线如图11 所示。可知轴承摩擦力随时间的增长，呈近似的正弦波动。相比于稳态下的轴承摩擦力，受到横向振动后的轴承摩擦力最大增幅为3.46%，最大降幅为1.479%。总体来说该工况下，横向振动对轴承摩擦力影响不大。

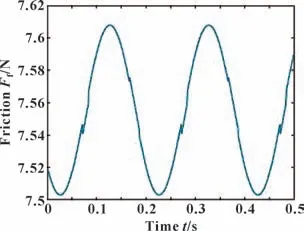
图11 轴承摩擦力波动曲线（εg＝0.3）Fig.11 The friction wave curve of bearing（εg＝0.3）

受到横向振动后，轴承摩擦因数的波动幅度比β按照式（24）计算：

式中：fmax为最大摩擦因数；fmin为最小摩擦因数；fave为平均摩擦因数。

轴承摩擦因数的波动幅度比β随横向振动程度的变化曲线如图12 所示，随着偏心激励程度的增大，摩擦因数波动幅度比随之增大。当偏心激励幅值为0.5 时，摩擦因数波动幅度比达到7.19%。

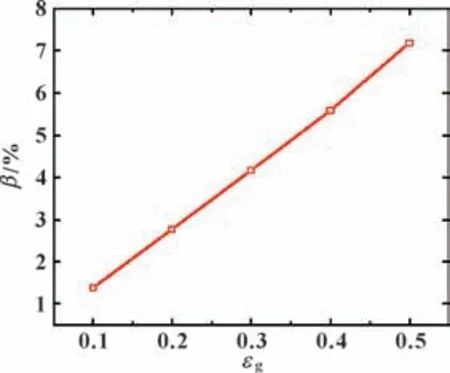
图12 摩擦因数波动幅度比随偏心激励幅值的变化Fig.12 Variation of the wave amplitude ratio of friction coefficient with the amplitude of eccentric excitation

不同横向振动程度下摩擦力的最大值、平均值和最小值变化趋势如图13 所示。可以看出，稳态下的摩擦力和受到振动影响后摩擦力的平均值几乎相同，不同振动程度下摩擦力平均值的相对差均小于1%。随着偏心激励幅值由0.1 增长到0.5，轴承的最大摩擦力增幅为2.94%，最小摩擦力的降幅为2.82%。总体来看，动压润滑条件下，轴承横向振动对轴承摩擦力的影响较小，偏心激励为0.5 时的平均动摩擦因数为0.003。

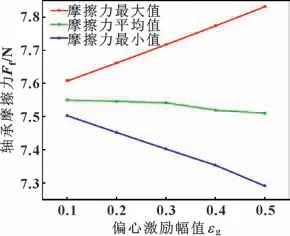
图13 不同振动程度下的轴承摩擦力Fig.13 Bearing friction force under different vibration levels

2.4 混合润滑下横向振动对轴承摩擦力的影响

将表5 所示的基本尺寸参数与工况参数输入至轴承运动方程，求得接触下轴颈位移响应曲线。

轴承受到偏心激励后的位移变化曲线如图14 所示，轴承的水平与垂直方向位移随着时间呈正弦波动，x方向最小位移为2.386×10－5m，最大位移为5.42×10－4m。y方向最小位移为1.732×10－6m，最大位移为4.64×10－4m。

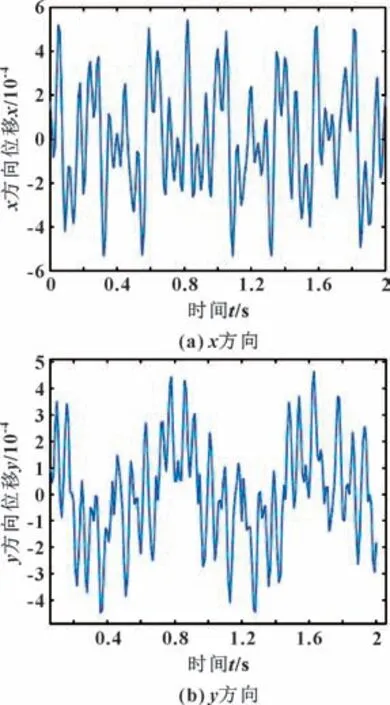
图14 位移时域响应Fig.14 Time domain response of displacement：（a） x direction；（b） y direction

将位移坐标转化为偏心率、偏位角输入混合润滑程序中计算承载力及摩擦因数。轴承受到偏心激励后2 s 内的摩擦力变化曲线如图15 所示。轴承的摩擦力随着时间的延长而波动变化，最小摩擦力为614.71 N，最大摩擦力为4 118 N，平均摩擦力为1 385.11 N；最小摩擦因数为0.016，最大摩擦因数为0.144，平均摩擦因数为0.030 9；平均承载合力为44 835.04 N。

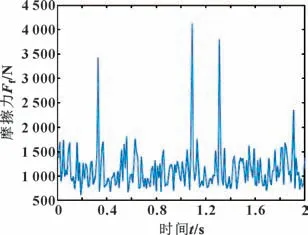
图15 摩擦力变化曲线Fig.15 Friction force variation curve

为了分析振动程度对混合润滑状态下轴承摩擦因数的影响，设置转速为196 r／min、偏心激励幅值为0.1、0.2、0.3、0.4 和0.5，分析混合润滑下横向振动程度对轴承摩擦力的影响规律。

以偏心激励幅值为0.3 的工况为例，轴承受到横向振动后的摩擦力变化曲线如图16 所示。可知轴承摩擦力出现较大波动，最大摩擦力为3 282 N，最小摩擦力为627.1 N。总体来说该工况下，横向振动对轴承摩擦力影响较大。

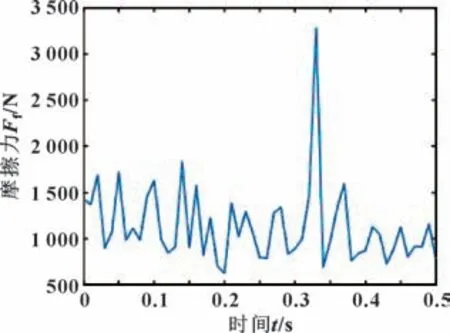
图16 横向振动下轴承摩擦力波动曲线（εg＝0.3）Fig.16 Friction wave curve of the bearing under transverse vibration（εg＝0.3）

轴承摩擦因数的波动幅度比β随横向振动程度的变化曲线如图17 所示。随着偏心激励程度的增大，摩擦因数波动幅度比随之增大；当偏心激励幅值为0.5 时，摩擦因数波动幅度比达到344.3%。

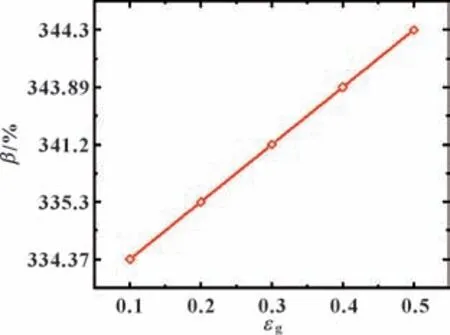
图17 摩擦因数波动幅度比随偏心激励幅值的变化Fig.17 Variation of the wave amplitude ratio of friction coefficient with the amplitude of eccentric excitation

不同横向振动程度下摩擦力的最大值、平均值和最小值变化趋势如图18 所示。可以看出接触条件下的轴承受到振动影响后摩擦力出现较大波动，不同振动程度下它们的波动幅度均大于300%。随着偏心激励幅值由0.1 增长到0.5，轴承的最大摩擦力增幅为7.6%，最小摩擦力增幅为6.5%，平均摩擦力由760.01 N 增加到911.07 N，增幅为6.7%。总体来看，接触条件下，轴承横向振动对轴承摩擦力的影响较大。

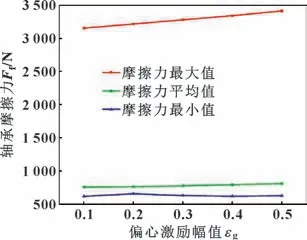
图18 不同振动程度下的轴承摩擦力Fig.18 Bearing friction force under different vibration levels

3 结论

针对某舰船推进系统中的水润滑轴承，根据轴系横向振动与轴承的相互关系，分别建立了流体动压润滑和混合润滑2 种状态下受横振影响的水润滑轴承动力学模型，通过算例，研究了不同激励幅值对轴承摩擦力的影响规律，得出了以下主要结论：

（1）水润滑轴承处于完全流体润滑状态时，轴承摩擦力主要是流体摩擦力，轴颈横向振动使轴承摩擦力和承载力呈近似正弦变化，相比稳态下的轴承状态，轴承的平均承载力有小幅增长。在偏心激励幅值由0.1 增长至0.5 的过程中，轴承摩擦力的波动幅度增幅最大约为3%。偏心激励幅值分别为0.1 和0.5时，轴承平均动摩擦力相对差小于1%。因此，当轴颈与轴承内衬没有接触时，横向振动对轴承摩擦力影响较弱，可忽略。

（2）水润滑轴承处于混合润滑状态时，轴承摩擦力由流体摩擦力与接触摩擦力组成，轴颈横向振动会影响轴承接触情况，导致轴承摩擦力呈现非线性变化。当偏心激励为0.5 时，轴承摩擦力的变化幅度达到334.3%，表明接触力相比水膜力对轴承摩擦力影响更大。随着偏心激励由0.1 增大至0.5，轴承平均动摩擦力增幅为6.7%，而摩擦力波动幅度比的增幅达到20.93%。因此，当轴承出现接触时，横向振动对轴承的摩擦力影响较显著，需要考虑。

（3）轴承没有接触时润滑状态是流体润滑状态。该状态下轴承受到振动后，轴心轨迹近似为椭圆；轴承出现接触，处于混合润滑状态，该状态下外界载荷由液膜力与接触力共同承担，轴心呈非线性运动轨迹。