考虑粗糙度的船舶水润滑高分子轴承弹流润滑性能研究∗

杨 浩 欧阳武 金 勇 邹 群

（1.武汉理工大学船海与能源动力工程学院 湖北武汉 430063；2.武汉理工大学交通与物流工程学院 湖北武汉 430063；3.国家水运安全工程技术研究中心，可靠性工程研究所 河北武汉 430063；4.中国舰船研究设计中心 湖北武汉 430064）

水润滑轴承是以自然水为润滑介质的一种轴承，它清洁无污染，而且可节约大量的油料和贵重有色金属，近年来在船舶、水泵、水轮机等设备上得到了广泛应用。目前，水润滑艉轴承材料一般为高分子聚合物，该类材料硬度低、弹性模量小，加之艉轴承工作在低速重载、启停机、高温高压等特殊工况下，在运行过程中轴承通常会产生粗糙接触，容易出现异常的振动噪声［1］。因此研究高分子水润滑轴承的润滑性能，不能忽略表面粗糙度这一因素。

国内外关于水润滑动静压滑动轴承润滑的研究较多，但对于考虑高分子轴承弹性变形下不同粗糙度的润滑状态的研究不够充分。目前，混合润滑状态中润滑膜压力的求解模型按照摩擦副表面形貌的不同表征方式可分为两类：统计学模型和确定性模型［2］。而对于水润滑滑动轴承等共形表面的混合润滑问题通常采用统计学模型。CUI 等［3］采用修正平均雷诺方程和Greenwood－Williamson 接触模型，研究了表面粗糙度对动压圆柱轴承启动时瞬态特性的影响，结果表明在启动初期粗糙接触压力不可忽略。刘洋洋等［4］研究了低速条件下表面粗糙度对水润滑轴承混合润滑性能的影响，结果表明低速工况下水润滑轴会承受较大的粗糙峰接触压力。ZHANG 等［5］对推力轴承粗糙表面进行分形描述，发现分形维数对混合润滑下摩擦学性能表征结果影响较大。XIE 等［6－7］通过理论和实验分析了不同工况下水润滑轴承的润滑状态，研究了不同外载荷、转速和径向间隙对摩擦因数和膜厚比的影响。曹玉哲等［8］建立了水润滑轴承混合润滑热模型，研究了长径比对重载水润滑轴承性能的影响。王艳真等［9］以计入弹性变形的流固耦合算法，对UHMWPE 基高分子复合材料水润滑轴承的润滑特性开展了研究。WANG 等［10］通过使用各种表面粗糙度参数模拟平均流量模型中的流动因子，研究了表面粗糙度特性参数对水润滑可倾瓦推力轴承流体承载能力的影响，表明流体承载能力受表面粗糙度特性参数的影响。

本文作者以高分子水润滑轴承为研究对象，建立了同时考虑弹性变形和粗糙度影响的水润滑轴承弹流混合润滑模型，得到了不同粗糙度下轴承的水膜厚度、偏心率、压力分布、承载力分布，分析了粗糙度变化对轴承润滑特性的影响，为水润滑轴承的优化设计提供理论参考。

1 模型建立

水润滑轴承结构如图1 所示。x、y分别代表轴承截面水平、垂直方向，轴承中心为O1，转轴绕轴颈中心O2转动，W为垂直方向载荷，ω为角速度，e为偏心距，ψ为偏位角，h为水膜间隙。

图1 水润滑轴承结构示意Fig.1 Schematic of water lubricated bearing structure

1.1 平均雷诺方程

船用艉轴承在低速、重载、低黏度润滑剂工况下最小名义膜厚会与表面粗糙度处于同一量级，此时轴承处于混合摩擦状态，平均流量模型无法适用，因此必须考虑压力流因子、剪切流因子和接触因子的影响，建立二维极坐标下混合流体动压润滑控制方程［11－12］，如式（1）所示。

式中：θ、λ为圆周方向和轴向方向，ϕθ、ϕλ为θ、λ方向的压力流量因子；ϕc为接触因子；ϕs为剪切流量因子；Rb为轴承半径；σ为轴和轴承两表面综合粗糙峰度的标准差；h为名义膜厚（轴和轴承两表面粗糙度中线间的距离）；p为水膜压力；η为水的黏度；us为主轴外表面的线速度。

1.2 膜厚方程与变形方程

根据正弦定理可得膜厚沿周向的分布公式为

式中：c为半径间隙；e为偏心距；ψ为偏位角；δ为弹性变形量。

弹性变形计算采用Winkler 法，控制方程为

式中：B为轴承内衬厚度；E为衬层弹性模量；ν为材料泊松比；p为水膜压力；pa为接触压力。

则膜厚比可表示为

式中：hmin为最小名义厚度；σ为粗糙度标准差；σ1为转轴粗糙度；σ2为轴承内衬粗糙度。

当1≤λ≤3 时，认为轴承处于混合润滑状态。

1.3 微凸体接触模型

固体接触压力的计算采用Greenwood 微凸体接触模型［13］：

式中：β为粗糙峰密度；D为粗糙面曲率半径；F2.5为不同膜厚比的分布函数；E∗为复合弹性模量。E∗、F2.5（h／σ）计算方法见式（6）（7）。

式中：ν1、ν2分别为轴承和轴颈的泊松比；E1、E2分别为轴承和轴颈的弹性模量。

1.4 承载力

水膜承载力、接触承载力计算方法见式（8）（9）。

式中：Foilx为水平水膜承载力；Foily为垂直水膜承载力；Aoil为完整水膜区；Faspx为水平接触承载力；Faspy为垂直接触承载力；Aasp为粗糙峰接触区。

2 计算流程与模型验证

通过有限差分法迭代求解水润滑轴承模型，其具体计算流程如图2 所示。进行数值求解时，首先假定偏心率及偏位角，通过划分网格后计算液膜厚度；然后采用适用于局部接触下的混合润滑流体计算的平均雷诺方程计算液膜压力，利用接触方程计算微凸峰接触压力，直至连续计算得到的压力值满足压力收敛条件；最后利用承载力平衡方程计算液膜动压力和微凸峰接触力，直至满足载荷平衡。在迭代过程中不断计算弹性变形后水膜厚度，通过计算粗糙峰接触方程划分得到接触区域和压力分布。

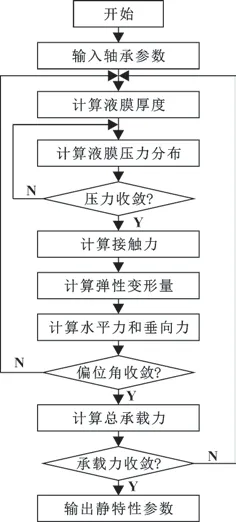
图2 计算流程Fig.2 Computational flow

采用文献［14］的轴承参数（如表1 所示）对文中模型进行验证。在相同工况下采用文中模型计算了纯流体动力润滑状态下的水膜压力，与文献［14］中轴颈倾斜角为0 情况下的液膜压力进行了对比。文中计算的压力峰值为33.4 MPa，文献［14］的压力峰值为33.1 MPa，结果与其文献值较为接近，验证了文中模型的可靠性。

表1 轴承基本参数［14］Table 1 Bearing basic parameters［14］

3 结果与讨论

文中研究了转速为400～1 200 r／min 时，轴承内衬不同粗糙度对水润滑轴承水膜最小名义膜厚、最大水膜压力、偏心率、压力分布的影响规律。目标轴承的主要参数如表2 所示。

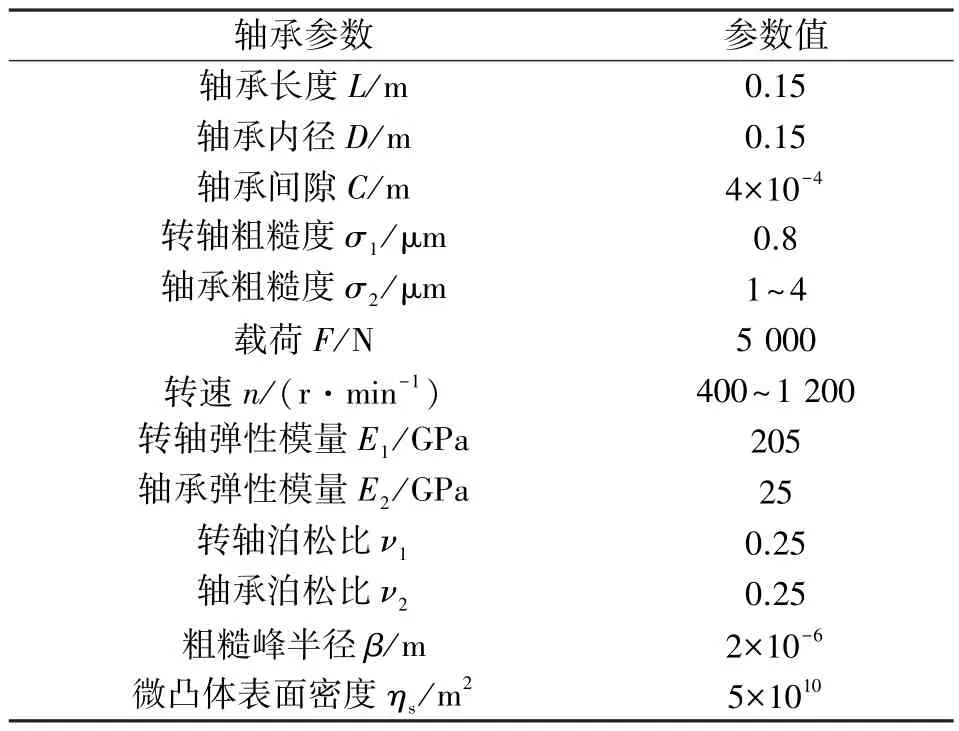
表2 算例轴承基本参数Table 2 Bearing basic parameters in the calculation example

3.1 水膜厚度变化

图3 给出了不同粗糙度下最小名义膜厚、偏心率与膜厚比随转速的变化。由图3（a）可知，随着转速升高最小膜厚均在上升，转速从400 r／min 提高到1 200 r／min，粗糙度为1 μm 时的最小膜厚从3.85 μm 增大至11.81 μm，粗糙度为4 μm 时的最小名义膜厚从12.52 μm 增大到13.95 μm。而相同转速下随着粗糙度增大最小膜厚随之增大，400 r／min 时粗糙度为4 μm 比粗糙度为1 μm 的最小名义膜厚增加了225.19%，1 200 r／min 时粗糙度为4 μm 比粗糙度为1 μm 的最小名义膜厚增加了18.12%。转速升高的过程中最小名义膜厚存在上升趋势，而且粗糙度越大最小名义膜厚的增幅越小。

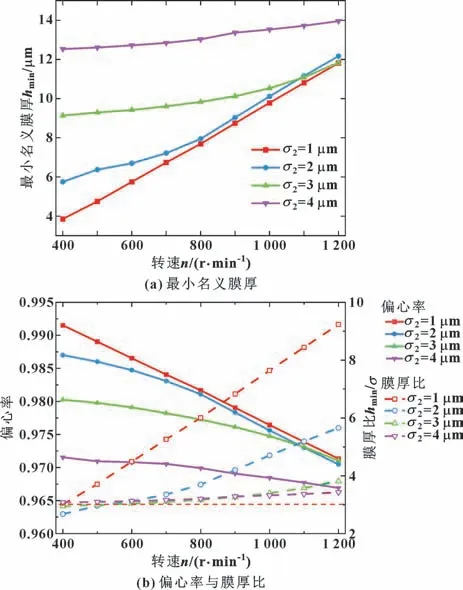
图3 不同粗糙度下最小名义膜厚、偏心率与膜厚比随转速的变化Fig.3 Variation of minimum nominal film thickness（a），eccentricity and film thickness ratio（b）with rotating speed at different surface roughness

当膜厚比小于3 时轴承处于混合润滑状态［9］，故设置图3（b）中膜厚比为3 的虚线表示弹流润滑与混合润滑状态的分界线。由图3（b）可知，当内衬粗糙度为3 和4 μm 时，水润滑轴承在400～500 r／min的工况下均处在混合润滑状态；随着转速升高，偏心率减小，轴颈被抬升，轴承逐步由混合润滑状态进入动压润滑状态。值得注意的是，内衬粗糙度为1 μm时，在各转速下均处于动压润滑状态，表明内衬粗糙度会影响轴承的“起飞转速”，即由混合润滑状态转变为动压润滑状态的转速。随着转速升高不同粗糙度的偏心率趋于一致，说明轴承在高转速下偏心率和膜厚受粗糙度影响很小。

3.2 水膜压力及接触压力变化

不同粗糙峰高度的轴承最大水膜压力pmax和最大固体接触压力pamax随转速变化曲线如图4 所示。400 r／min 转速下在各粗糙度轴承表面受到水膜压力和固体接触压力共同作用，而随着转速的提高，粗糙度1～3 μm 轴承的最大接触压力逐渐减小至0，说明随着转速的提升动压润滑状态改善，负载逐渐由水膜承担。在粗糙度为1 μm 时，轴承一直处在动压润滑状态，随着转速提高，水膜厚度提升，最大水膜压力逐渐减小；在粗糙度为2 和3 μm 时，水膜压力随着转速升高先增大后减小；而在粗糙度为4 μm 时最大水膜压力变化趋势与1 μm 相反，接触压力一直存在的情况下，随着转速增加最大水膜压力持续增大。上述结果表明，不同粗糙度下，最大水膜压力随转速的变化趋势不同，而最大接触压力均随着转速增高而下降。

图4 最大水膜压力和最大接触压力随转速的变化Fig.4 Variation of maximum water film pressure and maximum contact pressure with rotating speed

图5 所示为800 r／min 转速下不同粗糙度表面水膜压力和接触压力的分布。比较图5（a）和（b）可以看出，在粗糙度为1 和2 μm 时，接触压力接近于0，水膜最大压力主要分布在中心区域，在轴向1／2处对称分布；粗糙度从1 μm 增大到2 μm 时，水膜最大压力由3.17 MPa 变化到3.03 MPa，降低了4.4%，主要是由于轴承处于动压润滑状态下，粗糙度对其的影响较小。比较图5（c）和（d）可以看出，在粗糙度从3 μm 增大到4 μm 时，最大水膜压力从2.35 MPa 变化到1.61 MPa，降低了31.49%；而接触压力逐步增大，最大接触压力由1.52 MPa 增加到2.69 MPa，说明在转速一定情况下固体接触压力随粗糙度的增加而增大。

图5 800 r／min 转速下不同粗糙度表面的压力分布Fig.5 Pressure distribution of the surfaces with different roughness at 800 r／min：（a）roughness 1 μm；（b）roughness 2 μm；（c）roughness 3 μm；（d）roughness 4 μm

综上所述，随着转速的提升，轴承由混合润滑进入动压润滑阶段，接触压力将不断下降直至为0；而不同粗糙度轴承的水膜压力变化存在差异，较小的粗糙度可促进水膜压力的产生，增大流体承载区域水膜压力，促进水膜承载的主体作用，而且减少固体接触压力的强度。

3.3 承载力变化

在载荷不变的情况下，转速升高过程中不同粗糙度的水膜承载力变化曲线如图6 所示。可知，各粗糙度下水膜承载力与接触承载力呈相反变化趋势，即随着转速增加水膜承载力增加而接触承载力下降。在粗糙度分别为1、2、3、4 μm 时，400 r／min 下水膜承载力分别占总承载力的97.51%、74.57%、43.82%、31.42%，1 200 r／min 下水膜承载力分别占总承载力100%、99.91%、97.83%、80.54%。这说明在转速较低时由于水膜厚度较小，承载力主要由接触力提供；随转速增加水膜承载力逐渐增加，且转速增加轴承动压润滑效果增强，接触承载力逐渐降低，故水膜承载力占总承载力比例提高。由图6 还可看出，在相同转速下随粗糙峰高度的增大，水膜承载力减小，接触承载力增大。

图6 不同粗糙度下承载力随转速的变化Fig.6 Variation of bearing capacity with rotating speed at different surface roughness

4 结论

针对船用艉轴承服役时轴颈与轴承界面局部固体接触现象，建立水润滑艉轴承混合润滑模型，揭示轴承内衬表面粗糙度对不同转速下水润滑轴承的水膜最小厚厚度、水膜压力、接触压力和承载力等因素的影响规律，得到了以下主要结论：

（1）相同转速下，最小膜厚随粗糙度增大而增大。转速升高的过程中最小名义膜厚存在上升趋势，而且粗糙度的增大使最小名义膜厚的增幅减缓。

（2）随着转速的提升，轴承内衬粗糙度越小，其水膜越容易形成动压润滑，进而增大流体承载区域水膜压力，促进水膜承载的主体作用，减少固体接触压力的强度。

（3）水膜承载力随主轴转速增加而逐渐增大，接触承载力则随之减小。相同转速下，随着轴承粗糙度的增大，水膜承载力比例减少，接触承载力比例增大。