“双减”背景下初中数学课堂诊断与改进——以“垂径定理”教学为例

甘代祥, 吕瑜佩

(1.长兴县和平中学,浙江 长兴 313001;2.湖州师范学院 理学院,浙江 湖州 313000)

0 引 言

双减《意见》明确:“全面压减作业总量和时长,减轻学生过重的作业负担.”为此,在数学教学中,教师要更好地关注课堂教学环节,在教学理念、教学方法等方面进行创新和优化,为初中数学高效课堂提供良好的保障.

课堂诊断是实现教学理念和教学方法创新与优化的重要推手.2022年10月18日,长兴县和平中学邀请数学特级教师针对和平中学一位老师的“垂径定理”一课进行课堂诊断.整个诊断研讨过程拒绝空、虚、套,通过诊断找到课堂存在的问题,并进行归纳总结,尝试通过优化、调整问题的提问顺序和提问方式,增设问题的铺垫,加大课堂呈现的广度和深度,从而实现高效数学课堂,落实“双减”目标.

1 诊断研讨找问题

通过对“垂径定理”一课进行诊断和剖析,发现该课堂主要存在操作探究表面化、问题指向不明确、问题链设置不合理、问题设置铺垫少、缺少有效的课堂反馈等问题.

1.1 操作探究表面化

图1 题图

问题1圆是轴对称图形,它的对称轴是什么? 轴对称图形的性质是什么?(展示ppt)如图1所示,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为E.沿着直径所在的直线将圆对折,你会发现哪些点、线段、圆弧互相重合?(直接给出垂径定理,而对具体的证明过程,让学生课后去看书)

在课堂引入环节,教师试图用操作探究的方式来得出垂径定理.而实际却没有可操作的实物纸片圆,学生无法通过直观的观察得出结论,教师也没有对结论进行论证.

1.2 问题指向不明确

问题2图2是否具备垂径定理的条件?如果不具备,请说明理由.

图2 题图

“下列图形是否具备垂径定理的条件?”这个问题指向不明确,是具备垂径定理的一个条件还是全部条件?由于教师把问题设计得比较广、没有边际,所以学生无法领会老师的意图,导致无从下手或回答得不着边际[1],从而造成课堂冷场.此外,该问题设计没有涉及垂径定理的结论,割裂了问题的条件与结论的关联,因此无法起到巩固垂径定理和启发学生数学思维的作用.

1.3 问题链设置不合理

问题4如图3所示,已知排水管的半径OB=10,水面宽AB=16.求截面圆心O到水面的距离.

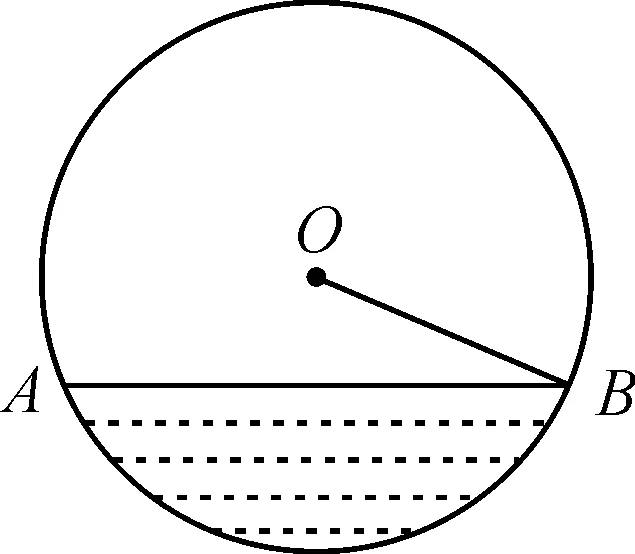
图3 题图

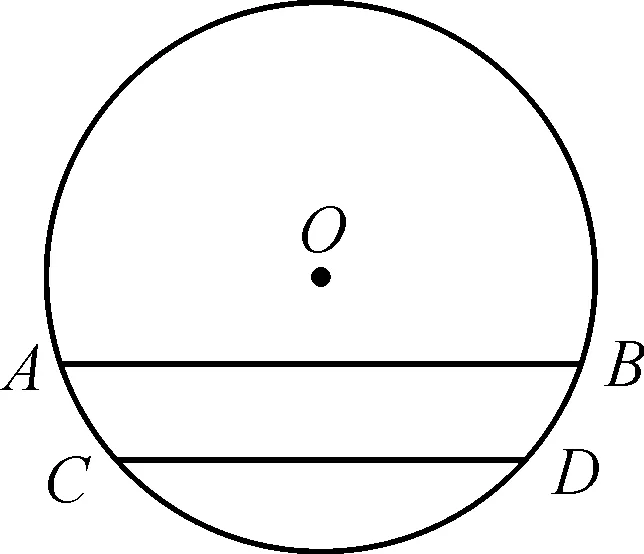
图4 题图

问题5由问题4的条件(已知半径、弦长)和问题(求弦心距),你能提出新的问题吗?

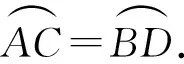
问题3到问题6之间的衔接不自然.问题3和问题6注重推理,而问题4和问题5侧重计算和应用.从推理到计算又到推理,这样的问题设计既不顺畅,又不合理.问题链的设计应该有层次地由浅入深、由易到难,通过问题的递进引导学生在逐层深入中获得知识、掌握知识,使他们思维的广阔性和深刻性同步得到提升[2].

1.4 问题设计铺垫少

教师直接抛出问题7:点A在⊙O内,过点A作一条弦BC,使弦BC是所有过点A的弦中最短的弦.虽然部分学生能在圆内尝试过点A画弦BC,但对什么情况下弦BC最短,大部分学生很难发现正确的结论.少数学生虽然能猜测到垂直于过A点的直径的弦BC是所有过点A的弦中最短的弦,但是无法说明理由.其原因是教师没有根据学生的认知水平对问题进行预设,对难度较大的问题缺少中间过渡步骤的铺垫,坡度太大,导致学生找不到探究问题的路径,从而错失问题设计的有效性.

1.5 缺少有效的课堂反馈

行为主义心理学认为:学习就是行动的反馈.因此,全面、及时、准确的信息反馈是提高学习效率的重要因素.笔者发现,本堂课在反馈上还存在以下问题:①不全面.教师以课堂上与个别学生点对点的交流回答,替代全班学生的学习信息反馈;②不多元.教师反馈的形式只有教师问、学生答这种形式,显得太单调;③不深入.教师重视反馈学生解题的结果,而忽视反馈解题过程中呈现的问题.

2 合力改进求高效

针对以上问题,教研组成员通力合作、认真思考、积极交流,对问题进行整合改进和再设计,从而让课堂更高效、更有深度.

2.1 提升操作探究的有效性

《数学课程标准》指出:“动手实践、自主探索、合作交流是学生数学学习的重要方式”.对“垂径定理”教学,如果教师通过操作活动让学生探究新知,不仅可以调动学生的求知欲,还可以使学生实现从感性实践到理性认识,变未知为已知.例如,本课例中的问题1可以做以下改进:

(1) 圆是一个特殊的图形,它特殊在哪里?你能画出它的对称轴吗?

(2) 请学生到黑板上画出对称轴.当学生画出垂直符号时,教师可追问:为什么要垂直?反之,则追问:这条直径有什么特别之处?

(3) 你能说说为什么沿着这条直线对折,图形的两边会重合?请大家将手上的图形按刚才的对称轴对折,并说明为什么垂直就会平分?我们之前在哪里学过类似的性质?

这个过程真正让学生动手操作,通过折叠让学生切身感受图形的重合.突出学生的主体地位,不仅有利于学生的主动学习和深度学习,还有利于学生思维的主动性和深刻性[3]．而通过追问则可以让学生回忆等腰三角形三线合一的性质,并由此想到连接两半径,从而利用重合证明垂径定理.将教学的落脚点放在追寻数学的本质上,不仅能让学生感受数学知识的关联性,还能帮助学生积累数学活动经验.

2.2 明确问题设置的指向性

问题设置的主要目的是引导学生的思考方向,提升他们解决问题的积极性,落实学生的主体地位.指向不明确的问题设置会让学生无法对提出的问题进行思考和作答.例如,本课例中的问题2可以做以下改进:

由下列各图形(图5),能否得到线段CE=DE?为什么?并追问:还能得到相等的弧吗?

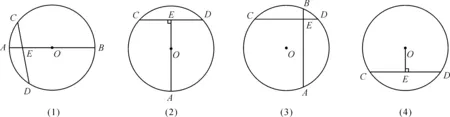
图5 题图

修改后,明确问题条件是圆中不同条件下的两条相交线段,结论是线段CE=DE是否相等.追问“为什么”“还能得到相等的弧吗?”能让学生自然地想到用垂径定理的条件,同时强调垂径定理的结论:垂直于弦的直径不仅平分弦,还平分弦所对的弧.这样的问题设计不仅有助于学生理清问题的条件和结论,还能有效巩固已学知识.

2.3 提升问题链的合理有效性

将问题以问题链的形式进行设计,不仅能够活跃学生的思维,还能够提升学生分析问题和解决问题的能力.例如,本课例中可以将问题4与问题6对调,并将问题6做以下改进:

在已知半径、弦长的情况下,能求弦心距和弓高,那你能完成以下题目吗?

(1) 如图6所示,OE=3,CD=8,试求⊙O的半径和弓高.

(2) 如图7所示,弓高EF=4,弦CD=16,试求圆O的半径和弦CD的弦心距.

(3) 如图8所示,⊙O的半径为13,弓高EF=8,试求弦CD的长和弦CD的弦心距.

图6 题图

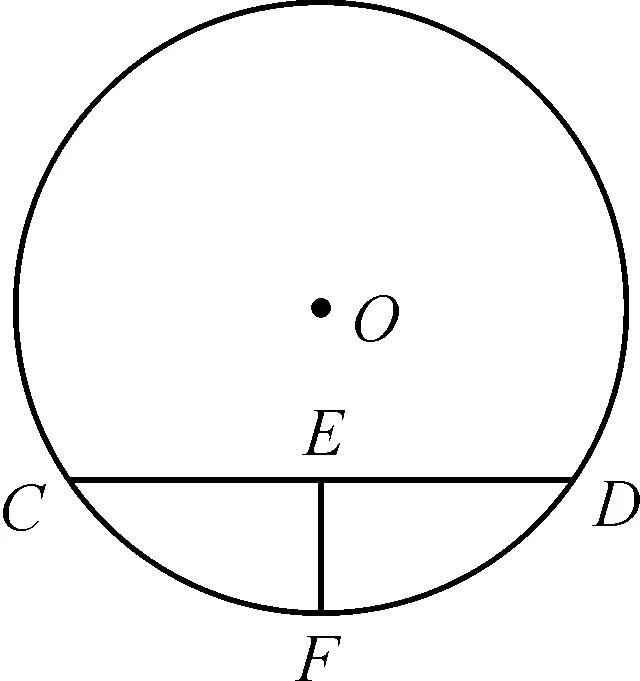
图7 题图

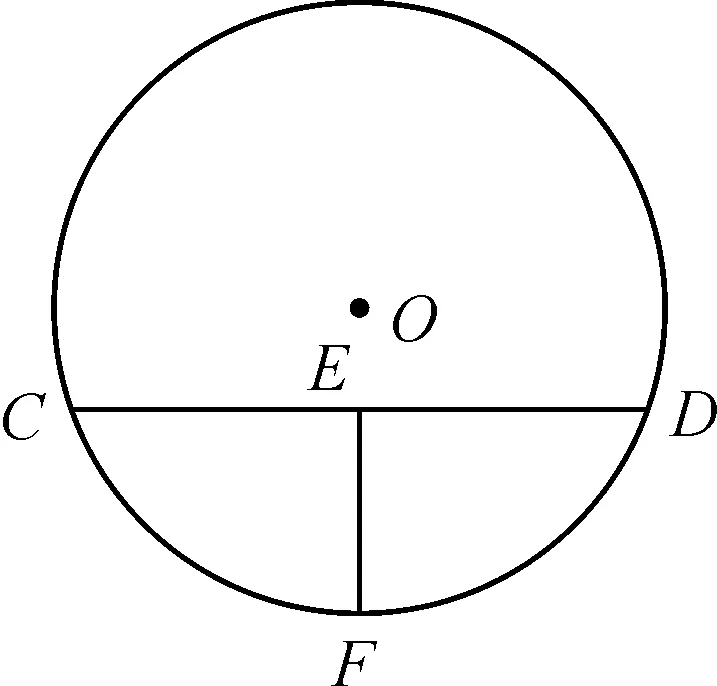
图8 题图

从问题3、问题4的垂径定理的理论应用到问题5、问题6的实际计算和应用,整个问题链衔接顺畅合理.同时,将问题6的提问具体化,能够让学生在解题过程中切实感受到“知二推二”,并可为难点问题7 的突破提供铺垫.

2.4 合理安排问题的梯度

对有一定难度的问题,问题设计不能突兀.因此,教师在问题设计时要注重层层递进,由易到难,环环相扣,从而发挥对学生的引导作用[4].例如,本课例中的问题7可以做以下改进:

图9 题图

(1) 点A在⊙O内,过点A作一条弦BC,过圆心作弦BC的弦心距OA1,你能将弦长BC用半径和弦心距表示吗?

(2) 根据基本图形中的勾股定理,在半径不变的情况下,过定点的半弦长的长短与弦心距的长短有什么关系?(学生回答后,拉动图9的几何画板进行直观验证)

(3) 要使弦最短,弦心距要满足什么条件?

(4) 现在你能不能过点A作一条弦BC,使弦BC是所有过点A的弦中最短的弦?

教师可通过设计一串有层次、有梯度的问题链来降低问题的难度,用合理的衔接和过度引导学生进行深入思考,并鼓励他们充分表达自己的想法.

2.5 落实课堂展示,关注目标达成

一节课的教学目标是否达成,在很大程度上取决于课堂展示的落实.教师应在课堂上让学生不断参与,通过操作探究让学生直观感受知识.例如,在本课例的操作环节,教师可以让学生上讲台展示折叠过程,在黑板演绎推理过程;利用投影展示学生解题中呈现的问题,鼓励学生分析问题产生的原因;通过分组分配进行任务展示,例如,在本课例的问题6中,教师可以以分组的形式让学生完成3个小题,并让小组推荐组员对知识进行归纳总结,力求让学生得出“知二推二”的结论.

3 诊后反思促评价

教学诊断能更好地促进课堂教学的高效,但要真正实现数学课堂高效且有深度,还需注意以下几点.

3.1 教学设计要合情合理

(1) 教学设计要符合学情.教师要认真把握任教班级学生的学情,掌握学生的认知水平和学习兴趣;根据学生实际的认知水平,考虑不同学生认知结构的差异,把握好教学的重点和难点;以学生的“最近发展区”为基础,引导学生将当前问题与已有认知进行类比、联系,使他们在认知冲突中不断深入学习情境,进而思考和解决问题.

(2) 教学设计要活用教材.叶圣陶先生说:“教材只能作为教课的依据,要教得好,使学生受益,还得靠教师的善于运用”.新课程标准要求教师“用教材教”,而不是“教教材”.“用教材教”要求以课标对教学知识的要求为基础,把知识教学伴随在培养学生数学能力、情感态度和价值观的过程中;在教学实践的过程中,从学生的实际和自己对教材知识结构的认识出发,合理地调整教材、取舍教材,把教材用活,真正做到教材为我所用,而不是被教材牵着走.

(3) 教学设计要突重破难.提高数学课堂教学效果的关键,是教师如何在有限的时间里实现突出教学重点、突破难点.要做到这一点,首先,要深钻教材,从知识结构上抓住重点和难点;其次,课前要精心准备、准确定位、合理引导,充分调动学生的学习积极性,为教学时突出重点和突破难点提供有利条件;再次,找准知识的生长点.数学是系统性很强的学科,数学教学要利用数学的严谨逻辑结构,引导学生实现由旧知到新知的迁移,促成从已知到未知的推理,不断完善认知结构.联系旧知找准新知的生长点,才能突出重点、突破难点.

3.2 问题设计要多维考量

(1) 问题设计要心中有生.教师如何设计问题才能让学生动起来,其中包括程度较差的学生.有效的问题设计,是把教师想说的话通过问题设计转化为学生的表达.教师不用太多的提示,只需抛出问题,静待花开,倾听学生的表达.

(2) 问题设计要分层递进.教师在问题设计时要按照学生的认知水平和教材的知识结构,将一些有难度的问题分解成若干紧密联系的小问题,引导学生由易到难,步步深入,让学生尝试主动思考和解决问题,直至获得成功的喜悦[5].

(3) 问题设计要形象直观.教师可利用几何画板等信息技术工具,在问题探究中多一点直观、形象的展示,少一些复杂的思维问题,使学生能逐步解决跳一跳就够得着的问题,从而养成积极思考的习惯,树立努力学习的信心.

(4) 问题设计要蕴含感悟.数学思维从何而来?从数学问题中来.如何用数学的语言表达现实世界?从数学问题的感悟中来.要使数学问题蕴含感悟,要让学生感悟数学知识的丰富内涵,如垂径定理不仅平分弦,还平分弦所对应的优弧和劣弧;要让学生感悟数学知识之间的密切关联,如垂径定理的计算要把条件汇聚到半弦长、半径和弦心距的直角三角形中,进而用勾股定理来计算;要让学生自己感悟探究的魅力.教师应时不时有意地让学生完成一些小探究,并及时写下探究感悟,使学生愿意去探究数学问题,并在此过程中感悟数学的真正魅力.

3.3 以学生为中心,优化评价体系

评价不仅要关注学生数学学习的结果,还要关注数学学习的过程,激励学生学习,改进教师教学[6].良好的数学教学评价体系不仅可以优化数学教学效果,还可以有效激发学生的数学学习热情.优化以学生为中心的评价体系,既能使学生的综合能力得到有效发展,又能提升学生数学学习的自信心.

(1) 利用多元化评价内容,实现学生数学学习兴趣的激发.多元化评价内容的构建,既可以真实地反映学生的学习情况,又可以提高学生对自我的认知.

(2) 结合多视角评价方法,实现学生数学学习能力的提升.在初中数学有效评价体系中,多视角的评价不仅能提升学生在数学学习中的数学情感、数学价值观和数学态度,使学生在数学学习过程中的成长发展有迹可循,还能让评价方式更有创新、更科学有效.

(3) 融合多渠道评价主体,实现初中数学教学效率的强化.在传统的数学教学评价体系建设中,不论是模式还是主体都是单项式的,不仅无法满足学生的发展需求,还不利于初中数学教学效率的提升[7].因此,教师可以确立多渠道的评价主体,让评价得到实质性的发展.例如,由学生、家长、教师、专家等共同参与的评价制度,不仅能提升教学效率,还能让学生在评价中清楚地认识自己的数学学习情况.

4 结 语

课堂诊断对高效课堂具有重要的促进作用,它可将教师的教和学生的学充分暴露.对课堂呈现的问题,教研组可以形成合力进行修改,对问题进行再设计和整合,同时反思如何优化数学教学的各个环节,使每个成员在诊断研讨中提升自己的教学研讨能力,从而使每一节数学课堂更加高效、更有深度.