计及储能荷电状态约束的输配协同机组组合优化

2023-12-05粟世玮胡钰焓

智慧电力 2023年11期

粟世玮，胡钰焓，王相，刘飞，熊炜

（1.三峡大学电气与新能源学院，湖北宜昌 443002；2.梯级水电站运行与控制湖北省重点实验室（三峡大学），湖北宜昌 443002；3.国网襄阳供电公司，湖北襄阳 441000）

0 引言

在世界能源供需格局变化和中国“双碳”目标背景下，分布式电源、储能等设施的接入，促使传统配电网变为主动配电网，输配电网耦合关系不断加深[1-4]。同时，输配割裂的传统运行方式不利于电网发展及双碳战略实施[5-8]。因此，实现输电网机组组合与配电网运行控制的协同对促进输配总体新能源消纳和保证系统安全稳定运行具有重要意义。

目前，传统的含储能机组组合研究相对来说比较成熟[9-13]。然而，传统的经济调度通常只从输电网角度考虑，把配电网当成固定负荷来进行研究，使得现有的输配电网分级调度不仅难以实现全局最优，而且还时常有弃风光的现象发生[14-16]。因此，如何在高精度、快速求解的大规模机组组合调度决策中考虑输配电网的协同运行，成为了机组组合面临的新挑战。

对于输配协同优化来说，大部分研究没有将其与机组组合问题中的启停计划联系起来，在一定程度上限制了输配协同运行经济性的提高。为此，国内外学者针对输配协同机组组合展开了一系列研究。文献[17-18]构建了电-气-热综合能源系统的输配协同机组组合模型，并采用目标级联法实现了输、配电网的解耦和并行优化。文献[19]为实现输配电网共赢，建立了主从博弈的输配电网双层经济调度模型。文献[20]根据SoS（System of Systems）概念，提出了输配协同下基于SoS 的安全约束机组组合框架。然而，现有的输配协同机组组合研究并没有计及储能的调节特性。

考虑到现有研究的不足，本文提出了一种基于交替方向乘子法（Alternating Direction Method of Multipliers Algorithm，ADMM）的计及储能荷电状态约束的输配协同机组组合双层优化模型。为提升多配电网接入输电网后的经济性，在配电网的并行优化中计及储能调节特性；为提高模型的求解效率，采用增量分段方法和二阶锥技术对模型中的非线性项进行线性化处理；为验证所提ADMM 算法的有效性，采用集中式算法和ADMM 算法对模型进行求解，结果验证了所提ADMM 算法准确度高、收敛性能好。

1 计及储能的输配协同调度框架

由图1 可以看出，输电网和配电网的利益主体不同，调度目标也不同，在进行经济调度时必须考虑到输配系统运行的强耦合性。为了达到输配协同集中式优化的目的，同时避免由于大量数据传输而导致的通信过载及数据丢失等问题，可采用式（1）对输配协同系统的边界联络线交换功率进行解耦。

图1 输配协同调度框架Fig.1 Scheduling framework for transmission and distribution coordination

2 输配协同的机组组合模型

在本文中，主要考虑输配电网总成本Ctotal最小：

式中：CTA为输电网运行成本；Nn为配电网数量；CDA,k为第k个配电网的运行成本。

2.1 输电网层优化模型

2.1.1 目标函数

输电网层的优化目标是使火电机组与风电出力相协调，提升输电网的经济性。其优化模型的目标函数如下：

式中：CTG，CGu，Cw，，Csell分别为火电机组燃料成本、火电机组启停成本、输电网弃风惩罚成本、污染物排放费用、输电网售电收益。

各项成本的具体表达式如下：

式中：ai，bi，ci为第i台火电机组的成本系数；为第i台火电机组t时刻的有功出力；si,t，hi,t分别为t时刻火电机组开、停机状态变量；分别为t时刻火电机组启、停机成本；αw为第w台风电机组弃风惩罚成本；，Pw,t分别为t时刻风电机组输出功率的预测值和实际值；为单位CO2价格；E∑，分别为输电网总CO2的排放量和碳排放配额；λk,t为t时刻输配边界的分时电价；NG，Nw分别火电机组、风电机组数量；T为机组组合时段总数。

2.1.2 约束条件

输电网层约束条件包括火电机组启停约束、出力约束、爬坡约束，以及风电场出力约束、输配电网联络线交换功率传输约束、功率平衡约束、线路潮流约束。其中，功率平衡约束见式（9），线路潮流约束见式（10），其他约束详见参考文献[17]。

2.2 配电网层优化模型

2.2.1 目标函数

配电网层的优化目标是通过储能来消纳更多的风电，减少从输电网购电的成本，从而提升配电网的经济性。以第k个配电网为例，其优化模型的目标函数如下：

式中：CCDG,k，CRDG,k，Cbuy,k，CESS,k分别为第k个配电网的可控分布式能源发电成本、分布式可再生能源弃风成本、向输电网购电成本、储能装置充放电损失成本。

各项成本的具体表达式如下：

式中：ak,g，bk,g，ck,g为第k个配电网中第g台可控分布式能源的成本系数；为第k个配电网中第g台可控分布式能源t时刻的有功出力；βh为第h台分布式可再生能源的弃风惩罚成本；分别为第h台分布式可再生能源t时刻的有功出力；分别为第k个配电网中储能装置的充、放电损耗成本系数；分别为第k个配电网中第m台储能装置t时刻的充、放电功率；NCDG，NRDG，NESS分别为可控分布式能源、分布式可再生能源、储能装置数目。

2.2.2 约束条件

配电网层的约束条件包括节点功率平衡约束、储能充放电功率约束、储能充放电状态约束、输配电网联络线交换功率传输约束、线路容量约束、储能荷电状态约束、配电网潮流约束等。其中储能荷电状态约束见式（16），配电网潮流约束见式（17），其他约束见文献[21-23]。

式中：σ为储能装置自损率；分别为第k个配电网中储能装置的充、放电效率；为第k个配电网中第m台储能装置容量；v(f)为以f为初始节点的支路末端节点的集合；Ve,t，Vf,t分别为t时刻节点e，f电压；Pef,t，Qef,t分别为t时刻从节点e流向节点f的有功、无功功率；xef，ref分别为支路e，f间的电抗、电阻；Pfj,t，Qfj,t分别为t时刻从节点f流向节点j的有功、无功功率；Δt为时间间隔，取1 h。

3 输配协同机组组合模型线性化处理

为提高模型的求解效率，采用增量分段方法对式（4）和式（12）中的非线性项进行线性化处理。以f(x)=x2为例，其中f(x)为分段点x对应的函数值，结合增量分段线性化如图2 给出增量分段方法的线性过程：

图2 增量分段线性化Fig.2 Diagram showing incremental piecewise linearization

式中：δs为第s个分段区间上的位置，取值为[0，1]；ηs为二进制变量；NPL为分段数；x1，x2，x3，xs，xs+1分别为计算分段线性化需要的第1，2，3，s，s+1 个分段离散点；f(x1)，f(x2)，f(x3)，f(xs)，f(xs+1)分别为分段离散点x1，x2，x3，xs，xs+1对应的函数值。

同时，由于配电网潮流约束是非凸非线性的，为调用求解器求解，需要采用二阶锥技术对其进行线性化处理。

首先，定义变量：

式中：Ief,t为t时刻从节点e流向节点f的电流；Ue,t为t时刻节点e电压。

然后，将式（22）代入式（17）中进一步松弛，得到：

最后，再进行等价变形，可将式（23）转化为潮流约束的二阶锥形式：

4 算例分析

4.1 算例参数设置

为验证本文算法的有效性，本文以24 h 的日前调度为例，对建立的输配协同机组组合模型以1 个IEEE 118 节点的输电网和3 个IEEE 33 节点的配电网为例进行算例分析。其中，输电网中火电机组的相关参数及线路参数来自文献[24]，配电网线路参数来自文献[25]，3 个配电网分别接在输电网节点49，64，89 上；集中式风电场分别接在输电网节点38，63，77 上，单装机容量为1 000 MW；分布式风电机组分别接在各配电网节点3，8，10，16，22，32 上，单台装机容量为400 kW；输配电网间的最大交换功率为1 000 kW；输配电网弃风惩罚成本为100 元/MWh，碳排放惩罚成本为2.5 元/t；ADMM 中惩罚因子设为0.08，对偶残差和原始残差的收敛精度设为0.5，对偶变量初值设为0。储能装置参数如表1 所示。

表1 储能装置参数Table 1 Parameters of energy storage device

4.2 优化结果分析

为验证储能装置接入配电网对输配协同的影响，本文构建2 种输配协同机组组合模型进行对比分析：（1）场景1，不考虑储能装置接入配电网；（2）场景2，考虑储能装置接入配电网。

4.2.1 系统成本分析

为分析储能装置对输配协同机组组合运行经济性的影响，表2 为采用ADMM 算法下2 种模型的系统成本。

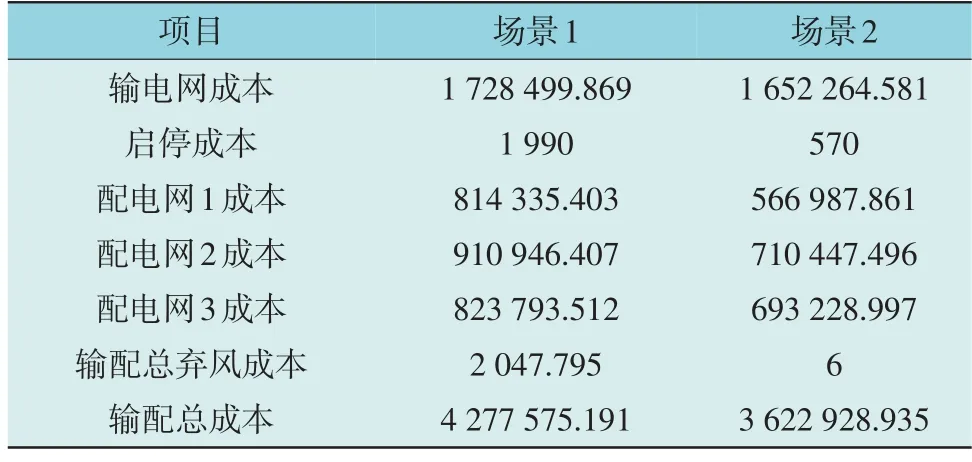
表2 2个场景的调度结果Table 2 Analysis of calculation results for two scenarios 元

由表2 可看出，场景1 中弃风成本、输配总成本及其他各项成本均是最高的，而场景2 中输电网成本、机组的启停成本均降低，这是因为储能装置接入配电网后发挥了其调节能力，分摊了电能需求，改善了输电网中火电机组的运行特性，避免了机组的频繁启停；配电网成本降低，是因为储能装置接入后，通过其时空转移的手段平抑了配电网负载的峰谷差；在弃风成本方面，场景1 中的机组只能通过弃风来满足功率平衡，而场景2 中储能装置的接入提高了配电网对风电的消纳能力，使得风电利用率提高、弃风成本降低。因此，储能装置接入配电网可以提升输配协同运行的经济性。

4.2.2 机组组合分析

为进一步分析储能装置接入配电网对输电网运行的影响，图3 给出了2 个场景下输电网中火电机组的启停计划，其中G1—G54 为54 台火电机组。2 个场景下各时段火电机组启动数如图4 所示。

图3 输电网火电机组启停计划Fig.3 Start-stop scheduling of thermal power unit in transmission grid

图4 各时段的火电机组启动数Fig.4 The number of thermal power unit starts by time period

由图3 和图4 可知，在输电网负荷高峰期，场景2 中火电机组的启动数比场景1 中少，而且机组是运行在低出力状态的。这是因为储能装置接入后，减轻了输电网中火电机组的负担，避免了火电机组的频繁启停，在提高风电消纳率的同时，也降低了输配电网的运行成本和弃风成本。

4.2.3 储能装置接入配电网后的调度结果分析

图5 为储能装置接入配电网后的调度结果。其中正值代表储能装置充电，负值代表储能装置放电。从图5 可以看出，由于1—5，13—17 时段是配电网负荷高峰期，风电出力不足，所以储能装置通过放电来补偿发电不足；在6—10 时段，由于风电出力较多，配电网负荷不能完全消纳，所以储能装置通过充电来储存多余的风电。因此，储能装置接入配电网后可根据负荷以及分布式可再生能源的出力实时调整功率分布，不仅可以避免发生弃风现象，而且也可以减少向输电网购买功率的成本。

图5 储能装置调度结果Fig.5 Scheduling results of energy storage device

4.3 ADMM算法与集中式算法的结果对比分析

为分析2 种算法对场景2 下运行经济性的影响，表3 给出了场景2 下2 种算法的优化调度结果。

表3 2种算法调度结果Table 3 Scheduling results of two algorithms

由表3 可知，从迭代次数和迭代时间来看，ADMM算法迭代次数为137 次，求解时间为4 632.75 s，相比于集中式算法来说，ADMM 算法在求解效率方面稍逊，这是因为集中式算法不需要进行迭代计算，因此计算时间短。但是输配电网往往属于不同的调度管理中心，出于对信息私密性的保护，集中式算法很难获得输配电网的准确信息，而ADMM 算法仅需交换边界联络线功率，避免了集中式算法数据量大、模型复杂及难求解等问题。此外，2 种算法得到的输配电网总成本很接近，其输配总成本的偏差仅为-0.087%，表明ADMM 算法在求解计及储能荷电状态约束的输配协同机组组合优化模型方面收敛性良好，偏差为负主要是因为ADMM 将大规模的输配整体优化模型分解为输、配电网子问题进行求解，降低了计算复杂度，因此ADMM 算法的输配总成本调度结果比集中式算法好。

场景2 下2 种算法总的联络线交换功率对比结果如图6 所示。

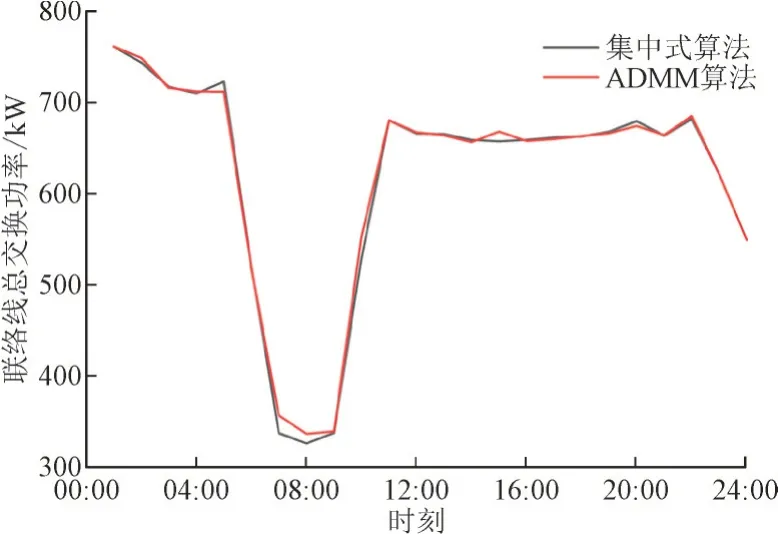
图6 2种算法总的联络线交换功率对比Fig.6 Comparison of the total tie-line exchange power between two algorithms

由图6 可以看出，在2，6，8，9，11，15 时刻，2 种算法得到的联络线总交换功率存在差异，但最大差值仅为23.989 kW，而图6 中其他时刻联络线交换功率大小是基本相同的，说明ADMM 算法可准确反映边界传输的信息。尽管在某些时刻2 种算法的联络线交换功率不太一样，但结合表3 可知，2 种算法下输配总成本的偏差仅为-0.087%，且ADMM 算法的总成本比集中式算法的总成本还要低，说明ADMM 算法具有良好的收敛性。