面向单基地MIMO 雷达的展开增广互质阵设计:低互耦和高自由度
2023-12-04郝鸿浩韩盛欣来张小飞
郝鸿浩,赖 欣,韩盛欣来,张小飞
南京航空航天大学电子信息工程学院,江苏南京210016
波达方向(direction of arrival,DOA)估计是阵列信号处理的重要内容,在无线通信、雷达、医学影像、声纳等方面有着重要的应用[1]。多输入多输出(multiple input multiple output,MIMO)雷达是一种新体制雷达,与传统相控阵雷达相比,MIMO 雷达具有更好的空间分辨率和参数的可识别性,在阵列信号处理方面引起了广泛的重视[2]。起初,针对MIMO 雷达DOA 估计的研究建立在均匀线阵上,利用子空间算法,如多重信号分类(multiple signal classification,MUSIC)[3]或旋转不变性(estimation of signal parameters via rotational invariance technique,ESPRIT)[4]方法实现DOA 估计。但是均匀线阵的阵元间距为半波长或小于半波长,不仅限制了阵列孔径,而且会导致DOA 估计的自由度受制于实际物理阵元的数量。
稀疏阵列MIMO 雷达在提升阵列的自由度、降低阵元间互耦和系统成本等方面有着巨大的优势[5],常见的稀疏阵列包括最小冗余阵[6]、嵌套阵[7]和互质阵[8],稀疏阵列MIMO 雷达对提高DOA 估计的精确度和角度分辨力有着重要的研究价值。最小冗余阵MIMO 雷达[9]的发射阵列和接收阵列均采用最小冗余阵,然而最小冗余阵没有闭式解,一般采用穷举法确定其物理阵元的位置,其计算复杂度高,在实际工程中难以运用;嵌套阵MIMO 雷达[10]的发射阵列和接收阵列均采用嵌套阵,然而嵌套阵MIMO 雷达存在密布阵,而密布阵受互耦影响较大,从而降低了DOA 估计的性能;互质阵MIMO 雷达[11]的发射阵列和接收阵列均采用互质阵,虽然互质阵的互耦更小,但是互质阵的两个子阵间是相互交错分布的,交错分布的子阵同样易受到互耦的影响,也会降低DOA 估计的性能。
互质阵在进行DOA 估计时的优势在于存在闭式解,并且互耦效应也优于嵌套阵,而不足之处在于接收数据协方差矩阵中连续自由度低,对此学者们进行了大量研究与改进。最简单的方法是将一个子阵的阵元数加倍,其他条件不变,这种阵型称为增广互质阵(augmented coprime array,ACA)[12]。随后又出现了广义互质阵(generalized coprime array,GCA)[13],具体分为两种:一种是将一个子阵的阵元间距压缩,这种阵型称为CACIS (coprime array with compressed inter-elemment spacing),且压缩因子越大,连续自由度越高;另一种是将一个子阵移至距另一个子阵一定距离的位置,这种阵型称为CADiS (coprime array with displaced subarrays),该阵列虽然不能增加自由度,但是解决了子阵阵元交错带来的高互耦的问题。后来提出的展开互质阵(unfolded coprime array,UCA)[14],也可以看成CADiS 的一种特殊形式,它实际上就是将互质阵的两个子阵按照相反方向分开放置。随着互质阵的不断改进与发展,如何利用互质阵实现高分辨率的MIMO 雷达成为了近年来的研究热点。文献[11] 设计的MIMO 雷达在收发两端分别部署互质阵,实现了入射角和发射角的联合估计,是一种最经典的互质阵MIMO 雷达,其互耦效应和自由度有待于进一步优化。文献[2] 设计的MIMO 雷达在收发两端部署增广互质阵,在发射端引入扩展因子α,进一步扩大了发射阵列的孔径,有效提升了DOA 估计的自由度,降低了发射阵元间的互耦,并且详细推导出了MIMO 雷达的闭式解,但是并没有解决接收阵列中子阵交错的问题。文献[1] 首次将展开互质阵与MIMO雷达相结合,在阵列中没有相近阵元的前提下实现了一定的连续自由度,降低了互耦的影响,但是文中提出的MIMO 雷达没有引入扩展因子,所以在自由度方面远不及文献[2] 所提出的MIMO 雷达。文献[15] 提出了一种基于互质阵MIMO 雷达的酉ESPRIT 算法,它将互质阵的两个子阵分别作为收发阵列,阵列结构简单而且不存在相近阵元,不需要进行空间平滑即实现了高精度的DOA 估计,其缺点是自由度低。文献[16] 系统分析了稀疏阵列MIMO 雷达设计规律,并提出了一种名为SA-FIS (sparse arrays with flexible inter-element spacing) 的雷达设计方式,它在收发阵列中分别引入了互质的扩展因子提高了阵元间距,其优点是阵列的设计更加灵活,不受制于阵元个数的限制,获得了更多的自由度同时降低了互耦的影响,缺点是连续自由度低,需要较为复杂的算法进行DOA 估计。
为了进一步降低MIMO 雷达阵列互耦影响,并提高连续自由度,本文利用稀疏扩展因子对展开增广互质阵列进行扩展,提出了展开增广互质MIMO 雷达结构。本文的贡献总结如下:1)通过引入稀疏扩展因子,使展开增广互质阵列的子阵的阵元间隔得到扩展,提出了展开增广互质MIMO 雷达。2)通过对展开增广互质阵列MIMO 雷达的广义和差联合阵列(generalized sum and different co-array,GSDC)[17]进行分析,详细推导出了连续自由度和总自由度的闭式解。3)通过性能分析与仿真结果验证了展开增广互质阵列MIMO 雷达DOA 估计上的优势。
1 信号模型
根据广义和差联合阵列的概念[16],一个MIMO 雷达最终得到的虚拟阵列既可以看成收发阵列差阵的和阵列,也可以看成收发阵列和阵的差阵列。差联合阵列定义为一个阵列中任意元素与任意元素之间所有不同的差,用公式可以表示为Sdc={u-u′,u,u′∈Su},其中Su表示一个阵列中阵元的实际位置[18];和联合阵列定义为一个阵列中任意元素与另一个阵列中任意元素之间所有不同的和,用公式可以表示为Ssc={u1+u2,u1∈S1;u2∈S2},其中S1和S2分别表示收发阵列中阵元的实际位置[18]。MIMO 雷达的一个重要优势就是可以利用和差联合阵列来扩展阵列结构,提高自由度。
如图1(a) 所示,考虑一个稀疏布阵的MIMO 雷达,它的发射阵元数N=3,阵元间距为半波长,接收阵元数M=2,阵元间距为3 倍的半波长,并且收发阵列相近放置,所以远场目标相对于收发阵列的角度是相同的。假设空间中有K个远场窄带不相干目标,第k(k=1,2,···,K) 个目标的角度为θk,发射与接收目标的角度集合分别为ST和SR,其中,ST={dt1,dt2,···,dtN,SR={dr1,dr2,···,drM}。

图1 稀疏阵列MIMO 雷达以及产生的虚拟阵列Figure 1 Sparse array MIMO radar and its virtual array
MIMO 雷达的回波信号模型可以表示为[13]
式中:s(t)=[s1(t),s2(t),···,sK(t)]T∈CK×1,sK(t) 是第K个目标的反射系数;n(t)∈CMN×1是接收信号中的加性高斯白噪声,高斯白噪声均值为0,方差为;A=At⊙Ar,At=[at(θ1),at(θ2),···,at(θk)],Ar=[ar(θ1),ar(θ2),···,ar(θk)],⊗和⊙分别表示Kronecker 积和Khatri-Rao 积,at(θk) 和ar(θk) 分别为第k个目标的发射导向矢量和接收导向矢量,具体可以表示为
式中:λ为波长。根据式(1),矩阵A=At⊙Ar的虚拟阵元位置由收发阵列的和阵组成,如图1(b) 所示,可以用集合P表示,P={nMd0+mNd0|0 ≤n≤N-1,0 ≤m≤M-1},d0为阵元间的单位间距。
接收信号的协方差矩阵可以表示为[2]
式中:I表示单位矩阵;Rs=E[s(t)sH(t)]=为目标协方差矩阵;diag()表示对角化;σ2K为第k个目标的信号能量。实际中,通常通过L个有限的快拍数获得协方差矩阵
向量化协方差矩阵Rx可得[13]
式中:k=1,2,···,K。
根据协方差矩阵的性质可知,矩阵A0=A∗⊙A的虚拟阵元位置由集合P的差阵组成,可以用公式表示为:SP={u-u′|u,u′∈P}。因为集合P代表了收发阵列的和联合阵列,所以结合式(7) 可知集合SP代表了收发阵列产生的和差联合阵列,如图1(c) 所示,即MIMO雷达最终能够产生的虚拟阵列的位置。
2 展开增广互质MIMO 雷达
2.1 展开增广互质阵列
互质阵是由阵元数和阵元间距均互质的两个稀疏线阵组成的[8],它的优势在于存在闭式解,互耦效应比嵌套阵更小,缺点是差联合阵列得到的连续虚拟阵列数目少,即连续自由度低。增广互质阵是在互质阵的基础对一个稀疏线阵的阵元间距进行压缩或者将一个稀疏线阵的阵元数加倍,其他条件不变,保持阵元数和阵元间距的互质关系[12]。增广互质阵可以提高连续自由度,提高角度分辨率,但是增大了一些互耦影响。两者DOA 估计的性能相近,图2给出了阵元数为6 时互质阵和增广互质阵的结构,阵列的孔径大小均为9。
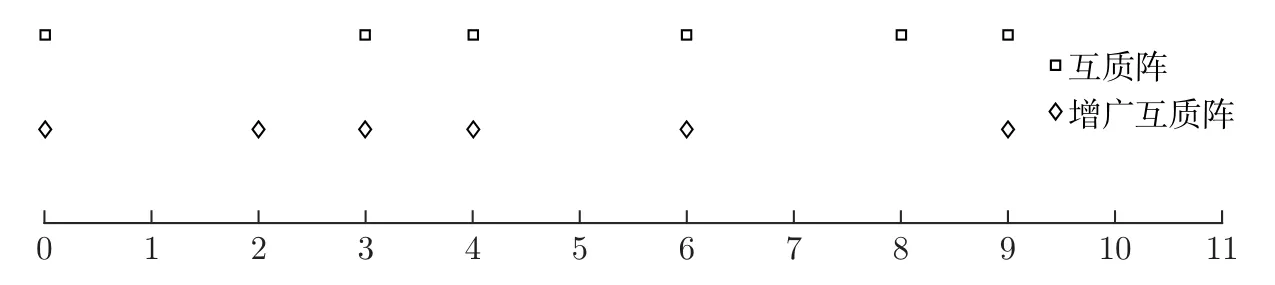
图2 互质阵和增广互质阵结构Figure 2 Structure of co-prime array and augmented co-prime array
展开增广互质阵实际上就是将传统互质阵的两个子阵按照相反方向展开排序[19],展开增广互质阵不仅增大了阵列的物理孔径,而且有效解决了子阵交错的问题,降低了互耦的影响,但同时也降低了阵列的连续自由度,所以不能用常规的子空间算法直接进行DOA 估计。图3给出了阵元数为6 时展开增广互质阵的结构,它的阵列孔径进一步扩大达到13。根据之前的介绍,MIMO 雷达的重要优势是可以利用和差联合阵列扩展虚拟阵列的结构提高自由度,因此将展开增广互质阵与MIMO 雷达结合,能够兼顾低互耦和高自由度,充分利用展开增广互质阵低互耦的优点,并且利用MIMO 雷达的特点弥补了其自由度低的缺点。文献[2] 将扩展因子α引入到了发射阵列中,充分利用了阵列的稀疏性,进一步提高了DOA 的自由度。在此基础上,本文同样引入了扩展因子α,并且将扩展因子同时引入到了发射阵列和接收阵列中,进一步提高了自由度降低了互耦。

图3 展开增广互质阵结构Figure 3 Structure of unfolded augmented co-prime array
2.2 展开增广互质阵MIMO 雷达
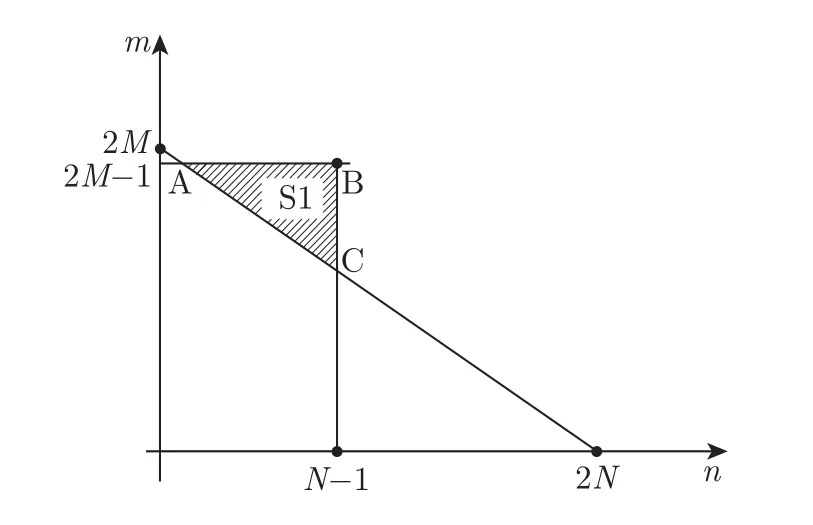
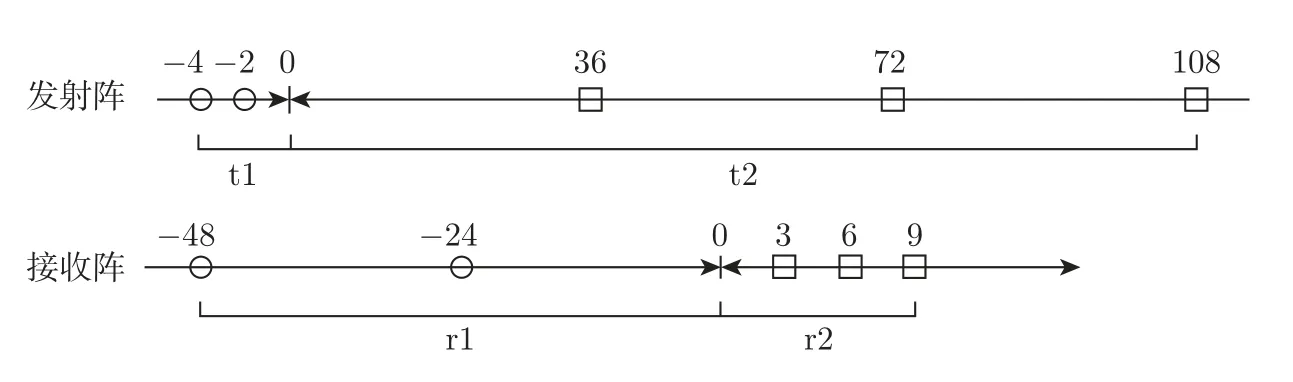
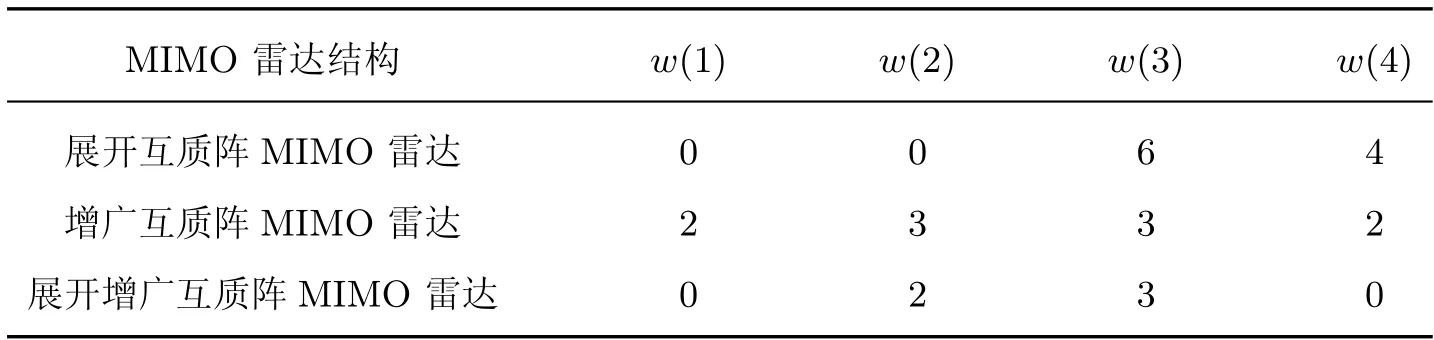
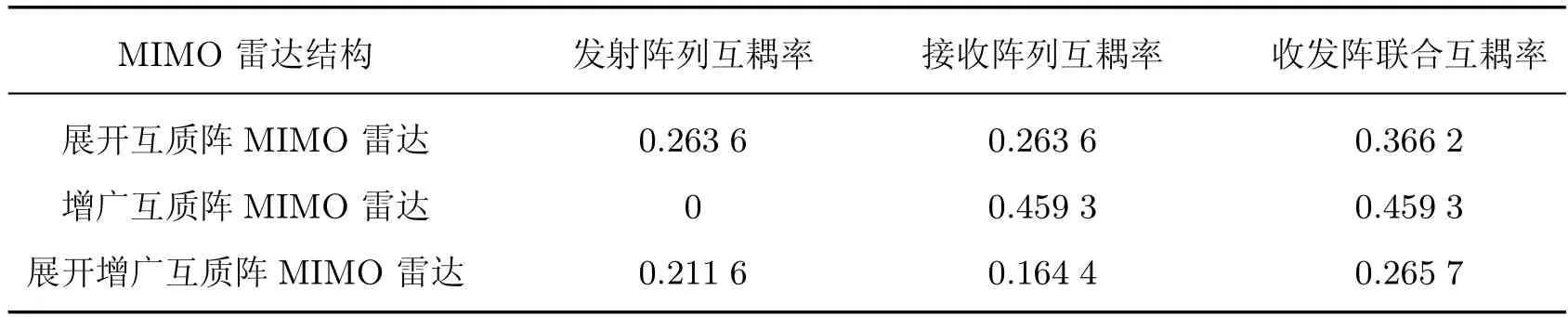
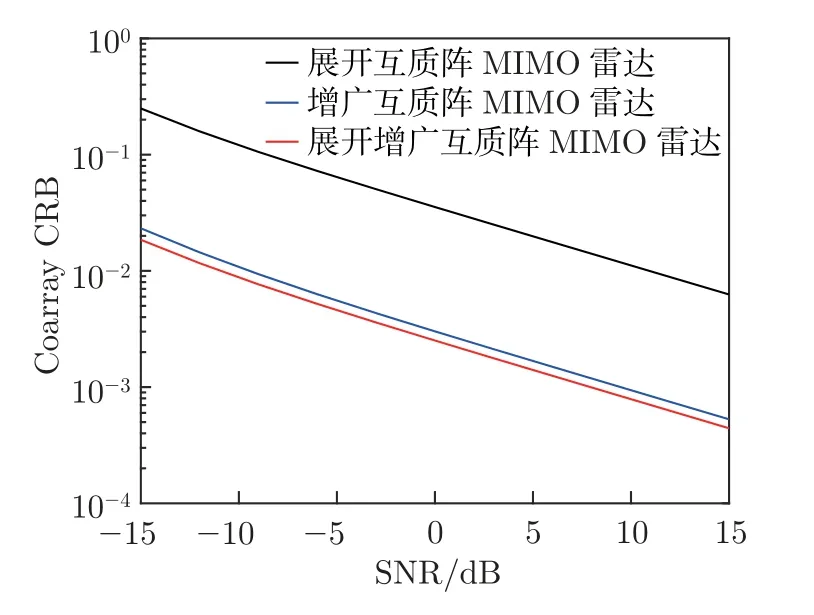
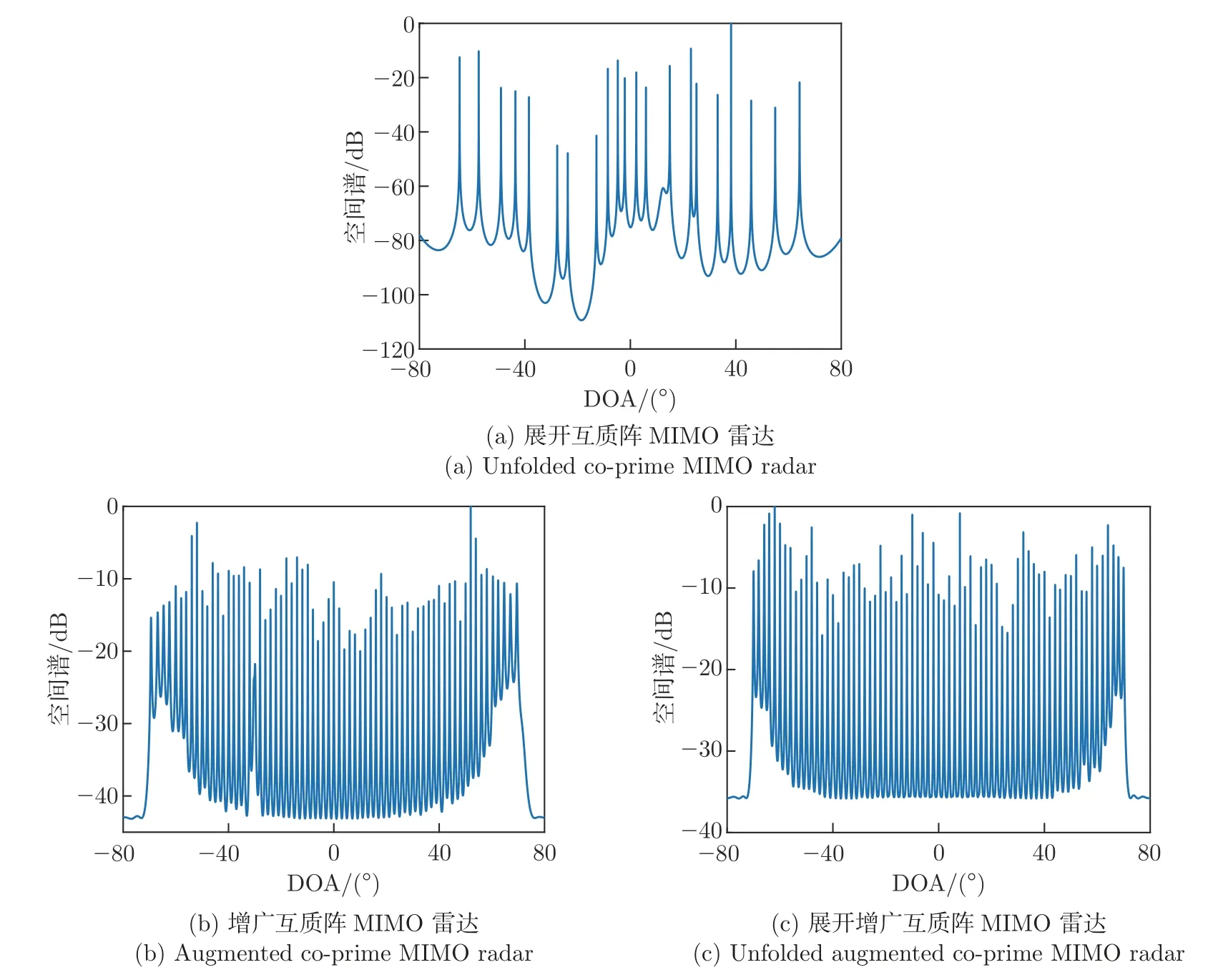
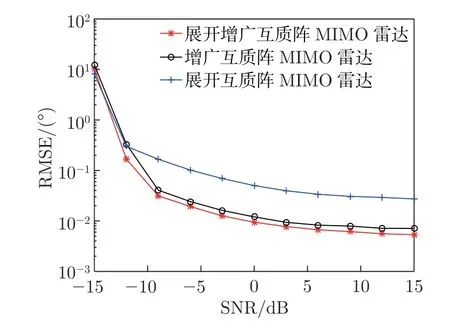
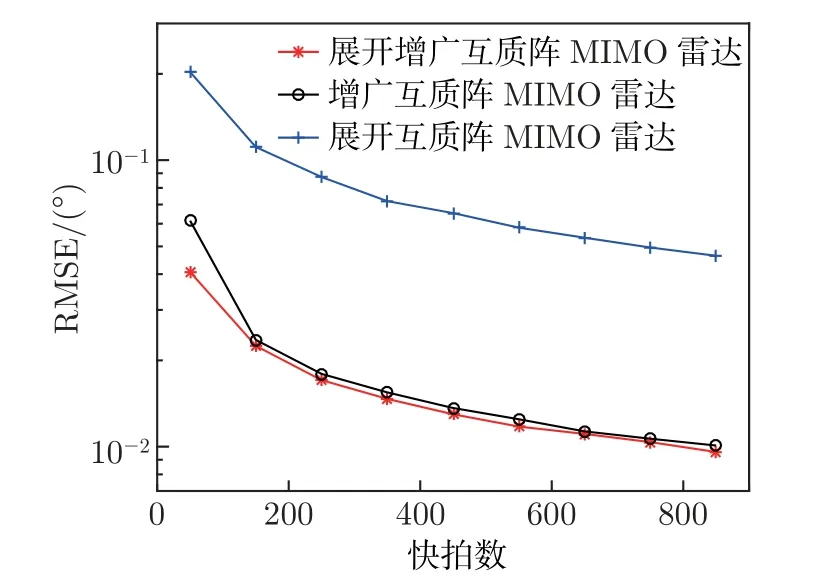
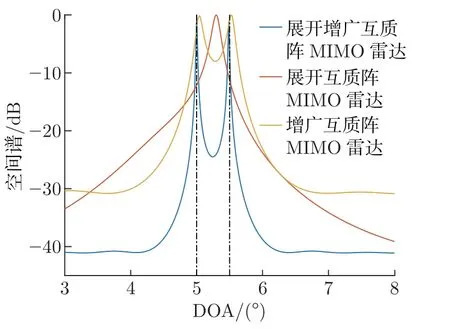
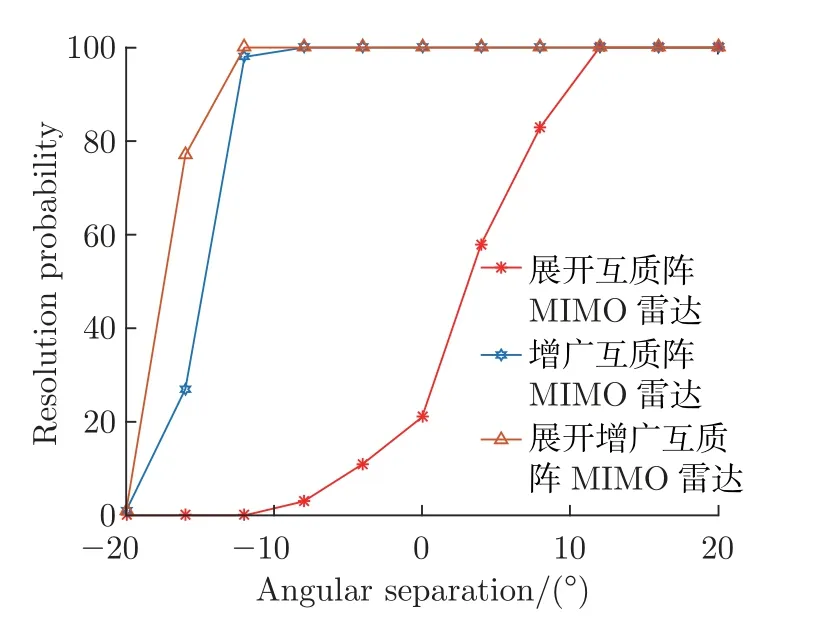
如图4 所示,考虑一个单基地展开增广互质阵列MIMO 雷达。展开增广互质阵列由2 个子阵组成,子阵1 包含N个阵元,子阵2 包含2M个阵元,两者互不交叉,并且共用一个阵元,所以收发阵列均由2M+N-1 个阵元组成,其中,M和N为互质数,且M 图4 展开增广互质阵MIMO 雷达结构示意图Figure 4 Configuration of unfolded augmented co-prime MIMO radar 若将互质阵2 个子阵的共用阵元记为原点,则发射阵列的阵元位置集合Lt为 同样,接收阵列的阵元位置集合Lr为 根据以上分析,单快拍接收矢量z的虚拟阵元的集合SDCSC可以表示为 这里,SDCSC通过收发阵列差阵的和联合阵列计算得到的。集合SDCSC具有如下性质[2]: 性质1 1)lt-和lr-是对称的,因此,SDCSC也是对称的。 2)lt-的差值包含两个子阵各自的自差(Mn-MnorαMn-αNm) 和两个子阵间的互差±(αNm+Mn)。因为自差是包含在互差中的,所以我们可以使用±(αNm1+Mn1)来表示lt-;同样,我们也可以使用±(Nm2+αMn2) 来表示lr-,其中,0 ≤n1,n2≤N-1,0 ≤m1,m2≤2M-1。 最终,集合SDCSC还可表示为 因为集合SDCSC具有对称性,所以下文以正向虚拟阵元为例,来证明雷达能够实现的自由度,令集合L1={α(Nm1+Mn2)+(Mn1+Nm2)|0 ≤m1,m2≤2M-1,0 ≤n1,n2≤N-1},其中M,N是互质数,α=2MN是扩展因子,L1具有如下性质。 性质2 1)集合L1的连续虚拟阵元的范围为[2MN(MN-M-N+2),(2MN)2-1]。 2)集合L1中大于(2MN)2的非连续虚拟阵元数在M>2 时,为(2MN+1)[(M-2)(N-1-/)+2],·表示向上取整,在M=2 时为(2MN+1)。 证明: 首先,证明Nm+Mn,满足0 ≤m≤2M-1,0 ≤n≤N-1,M和N是互质数,具有如下性质。 ①有2MN个不同的整数,因为M和N的互质性使得m和n不同时,Nm+Mn的值必然不同。 ②0 ≤Nm+Mn≤3MN-M-N。 ③不存在距离相差2MN的两个点,即不存在m1,m2∈[0,2M-1],n1,n2∈[0,N-1],使得Nm1+Mn1-(Nm2+Mn2)=±2MN。 假设存在m1,m2和n1,n2使得Nm1+Mn1-(Nm2+Mn2)=2MN。将等式两端同时除以M,得N(m1-m2)/M+(n1-n2)=2N,其中N(m1-m2)/M只有当m1-m2取到±M时的值为整数,即±N。那么(n1-n2)=-N,3N,这与n1-n2∈[1-N,N-1] 相矛盾,所以不存在相距2MN的两个点。 ④Nm1+Mn1在[MN-M-N+1,2MN-1]连续,(-2MN+Nm2+Mn2)∪(Nm1+Mn1) 在[0,2MN-1] 连续。 由③可以推断出mod(Nm+Mn,2MN) 也具有2MN个不同的整数,所以mod(Nm+Mn,2MN)包含从0 到2MN-1 的所有整数,mod(·)表示取余数。说明Nm+Mn中所有在[2MN,3MN-M-N] 的数都可以减去2MN来填补Nm+Mn自身在[0,2MN-M-N]范围中所有的孔洞,即(-2MN+Nm2+Mn2)∪(Nm1+Mn1) 在[0,2MN-1] 连续。同样也说明,Nm+Mn在[MN-M-N+1,2MN-1] 上是连续的。 ⑤M>2 时,有(M-2)(N-1-/)+2 个大于2MN的数,M=2 时,仅有1 个大于2MN的数。 图5 中三角形阴影区域S1为直线Nm+Mn=2MN,n=N-1 和m=2MN-1围成的区域,阴影部分代表了在0 ≤m≤2M-1,0 ≤n≤N-1 的前提下,所有满足Nm+Mn>2MN的数的集合,实际中我们只需要考虑其中横纵坐标均为整数的点。A、B、C三点的坐标依次为(N/M,2M-1)、(N-1,2M-1)、(N-1,M+M/N),由于M和N的互质性,所以三角形的对角线上不存在整数点,阴影区域中的整数点的数目Snum可以将线段AB和线段BC向下取整后利用面积求得[13],当阴影面积为不为0 时Snum为线段AB和线段BC向下取整后的长度之积加2,即Snum=(M-2)(N-1-/)+2,若阴影面积为0,则Snum为线段AB和线段BC向下取整后的长度之和,即M=2 时,Snum=1。 图5 三条直线所围成的阴影区域S1Figure 5 Shaded region S1 surrounded by three lines 因为集合L1={α(Nm1+Mn2)+(Mn1+Nm2)},根据④可知,L1在[α(MN-M-N+2),α(2MN-1)+2MN-1] 上是连续的,即集合L1的连续虚拟阵元的范围为[2MN(MN-M-N+2),(2MN)2-1]。根据⑤可知,在M>2 时阴影面积不为0,集合L1中大于(2MN)2的虚拟阵元数为(2MN+1)[(M-1)(N-1-/)+2],当M=2 时,集合L1中大于(2MN)2的虚拟阵元数为(2MN+1)。证毕 令集合L2={α(Nm1-Mn2)-(Nm2-Mn1)|0 ≤m1,m2≤2M-1,0 ≤n1,n2≤N-1},L2具有如下性质。 性质3集合L2的连续虚拟阵元范围为[0,2MN(MN+M-1)]。 证明: 首先,Nm-Mn即为互质阵的差阵,满足0 ≤m≤2M-1,0 ≤n≤N-1,M和N是互质数,具有如下性质[8]。 ①有2MN个不同的整数; ②-M(N-1)≤Nm-Mn≤N(2M-1); ③在[-(N-1),MN+M-1] 连续; ④(Nm2-Mn2)+2MN ∪(Nm1-Mn1) 在[0,2MN-1] 连续。 因为集合L2={α(Nm1-Mn2)-(Nm2-Mn1)},根据③和④可知,L2在[0,α(MN+M-1)] 上是连续的,即集合L2的连续虚拟阵元的范围为[0,2MN(MN+M-1)]。证毕 最终可以得到SDCSC=±L1±L2,SDCSC具有如下性质。 性质4 1)集合SDCSC的连续自由度为2(2MN)2+1。 2)集合SDCSC的自由度为 证明: 因为2MN(MN+M-1)≥2MN(MN-M-N+2),即2M+N≥3 是显然成立的,所以集合SDCSC=±L1∪±L2的连续虚拟阵元的范围为[-((2MN)2-1),(2MN)2-1],连续自由度即为2(2MN)2+1。集合SDCSC中大于(2MN)2和小于-(2MN)2的虚拟阵元数相同,当M>2 时,集合SDCSC共有8M2N2-1+(2MN+1)(M-1)(N-1-/) 个不同的虚拟阵元,当M=2 时,集合SDCSC共有8M2N2-1+(2MN+1) 个不同的虚拟阵元,集合中虚拟阵元的个数即为阵列能够达到的总的自由度。证毕 本节将本文设计的展开增广互质阵MIMO 雷达与展开互质阵MIMO 雷达[1]和增广互质阵MIMO 雷达[2]进行比较,从自由度、互耦率和克拉美罗界(cramér-rao bound,CRB)这3 个方面对比得出本文所设计雷达的优势。 表1 给出了所提出的展开增广互质阵MIMO 雷达与展开互质阵MIMO 雷达和增广互质阵MIMO 雷达自由度和连续自由度方面的闭式表达式。为了方便分析与控制变量,取3 种MIMO 雷达的总阵元数均为12,因此取展开互质阵MIMO 雷达的M=3,N=4,发射阵元和接收阵元的位置为{-8,-4,0,3,6,9};取增广互质阵MIMO 雷达的M=2,N=3,发射阵元位置为{0,30,45,60,90,135},接收阵元位置为{0,2,3,4,6,9};取展开增广互质MIMO 雷达的M=2,N=3,图6 给出了该MIMO 雷达的结构。图7 给出了这3 种MIMO 雷达最终实现的虚拟阵列。 表1 不同互质阵列雷达结构的比较Table 1 Comparison of different co-prime array radar structures 图6 M=2,N=3 时展开增广互质阵MIMO 雷达的结构Figure 6 Configuration of unfolded augmented co-prime MIMO radar when M=2,N=3 图7 3 种MIMO 雷达产生的虚拟阵列Figure 7 Virtual arrays generated by three kinds of MIMO radars 表2 列出了在总阵元数为12 时,这3 种MIMO 雷达实现的自由度,从表中可以看出,展开增广互质阵MIMO 雷达的自由度更高。 表2 阵元数为12 时不同雷达的自由度Table 2 DOF of different radars when the total number of radar is 12 阵列的互耦率定义为[20] 式中:c为互耦矩阵,可近似为B带的Toeplitz 矩阵;I是与c同维度的单位矩阵 式中:cij为矩阵c的第i行第j列元素,且1=c0>|c1|>···>|cB|>|cB+1|=0;并且接收阵列与发射阵列的联合耦合系数矩阵为C=Ct⊗Cr,Ct和Cr分别表示发射阵列和接收阵列的互耦矩阵[21]。由式(13) 可知,Ω越小,表示阵列受到的互耦影响越低,角度估计的性能会越好。 现假设互耦矩阵中的元素满足c0=1,c1=0.5 ejπ/4,c2=0.5 ej0.5π/2,c3=0.5 ej0.5π/4,c4=0.5 ej0.5π/4,B=4。表3 列出了3 种MIMO 雷达权重函数中w(1)、w(2)、w(3)、w(4)的值,表4 列出了在此条件下,3 种MIMO 雷达收发阵列各自及联合的互耦率。从表中可以看出,展开增广互质阵MIMO 雷达的互耦率更低,其主要原因是因为收发阵列均采用展开的互质阵,权重函数的w(1)=0,w(2)=2,有效避免了相近阵元所带来的高互耦的影响,并且随着阵元数的增多,展开互质阵阵元间的间距会进一步扩大,优势会更加明显。 表3 雷达权重值的比较Table 3 Comparison of radar weight values 表4 雷达互耦率的比较Table 4 Comparison of mutual coupling rates of radars 克拉美罗界为任意无偏估计量的方差确定了一个下限,意味着无偏估计量的方差只能无限逼近CRB,而不会小于它,因此为无偏估计量的性能提供了一个标准。DOA 估计的CRB模型已经研究发展了数十年,包括了单基地MIMO 和双基地MIMO 模型,单径和多径信道模型,非相干信号、相干信号到混合信号模型等各种条件下的CRB 模型,根据文献[16] 的证明推导出的CRB 模型,图8 中给出了3 种MIMO 雷达在信噪比从-15∼15 dB 时的CRB曲线。从图中可以看出展开增广互质阵MIMO 雷达的CRB 曲线比其他两种MIMO 雷达的曲线对应的值更小,所以理论上本文设计的MIMO 雷达的DOA 误差更小,性能更好。 图8 3 种MIMO 雷达的CRB 曲线Figure 8 CRB curves of three kinds of MIMO radars 本节使用经典的空间平滑多重信号分类MUSIC 算法[3]进行DOA 估计的仿真实验。实验的场景设定与上文相同,收发阵元数皆为6,总阵元数为12,实验过程中保持接收阵列的信号功率为16 dBm,发射信号为高斯信号,信道的噪声模拟为加性高斯白噪声,并且不考虑阵元间互耦的影响。 MUSIC 算法是上世纪80 年代提出的一种经典高分辨率的方DOA 估计方法[22],它通过在空间域内进行谱峰搜索来确定信号源的方向。具体来说,MUSIC 算法的基本原理是导向矢量(θ) 与噪声子空间具有正交性,其大致步骤为:首先对协方差矩阵Rx进行特征值分解;然后按特征值的大小排序,将与信号个数相等的K个最大特征值对应的特征向量看成信号子空间,把剩下的特征值对应的特征向量看成噪声子空间,噪声子空间记为UN;最后,利用式构造出MUSIC 算法的空间谱函数。 接下来,我们对MIMO 雷达DOA 估计的空间谱、均方根误差(root mean square error,RMSE)随信噪比(signal to noise rate,SNR)、角度分辨力进行比较与分析。 图9 给出了3 种MIMO 雷达多目标DOA 估计的空间谱。假设空间存在71 个远场非相干目标,角度范围为[-70o: 2o: 70o],SNR 为10 dB,快拍数为500,搜索范围为[-80o,80o],步长为0.01o。从图中可以看出本文设计的MIMO 雷达可以估计远超出物理阵元总数的非相干目标,而且相较于其他两种MIMO 雷达,空间谱更加尖锐整齐。 图9 K=71 时获得的空间谱Figure 9 Spatial spectrum obtained with K=71 假设空间中存在8 个远场窄带不相干目标[-40o,-30o,-20o,-10o,10o,20o,30o,40o],均方根误差的计算公式为 图10 给出了不同MIMO 雷达DOA 估计得到的RMSE 随信噪比的变换情况,其中快拍数为500;图11 给出了不同MIMO 雷达DOA 估计得到的RMSE 随快拍数的变化情况,其中SNR 为0 dB。由图10 和11 可知,随着信噪比和快拍数的增加,角度估计的误差逐渐减小,在相同条件下,本文提出的展开增广互质阵MIMO 雷达的精确度更高,性能更好。 图10 RMSE 随SNR 的变化关系Figure 10 Variation relationship of RMSE with SNR 图11 RMSE 随快拍数的变化关系Figure 11 Variation relationship of RMSE with the number of snapshots 图12 对比了3 种MIMO 雷达的角度分辨力,其中2 个临近目标位置为5.0o和5.5o,SNR为0 dB,快拍数为100,搜索范围为[3o,8o],步长为0.01o,黑色虚线表示真实角度。从图12可以看出,展开互质阵无法分辨邻近的目标,而增广互质阵和展开增广互质阵可以分辨两个相邻0.5o的目标,并且展开增广互质阵的空间谱的谱峰更加尖锐,峰值也更加接近真实的角度估计。图13 给出了3 种MIMO 雷达在快拍数为500 时,随着信噪比的变化能够分辨出临近目标位置为5.0o和5.5o的概率,根据文献[23] 的描述,将满足的估计结果视为能够分辨出两个临近目标。从图中可以看出,展开增广互质阵在相同信噪比的情况下,能够分辨出相邻目标的概率更高,并且当信噪比大于-5 dB 时,能够有效分辨出相邻目标。 图12 两个空间相邻目标的空间谱Figure 12 Spatial spectra for two closely spacing sources 图13 3 种MIMO 雷达对相邻目标的分辨概率Figure 13 Resolution probability of three kinds of MIMO radars to adjacent targets 本文提出了一种展开增广互质MIMO 雷达结构。首先,通过引入稀疏扩展因子扩展展开增广互质阵列中子阵的阵元间隔,获得了展开增广互质MIMO 雷达的闭式表达式。然后通过对展开增广互质阵列MIMO 雷达的广义和差联合阵列进行分析,推导了连续自由度和总自由度的闭式解。相比其他互质MIMO 雷达,展开增广互质MIMO 雷达具有更低的互耦率和更多的连续自由度。仿真结果表明,本文提出的互质MIMO 雷达结构在DOA 估计性能与角度分辨力上具有一定优势。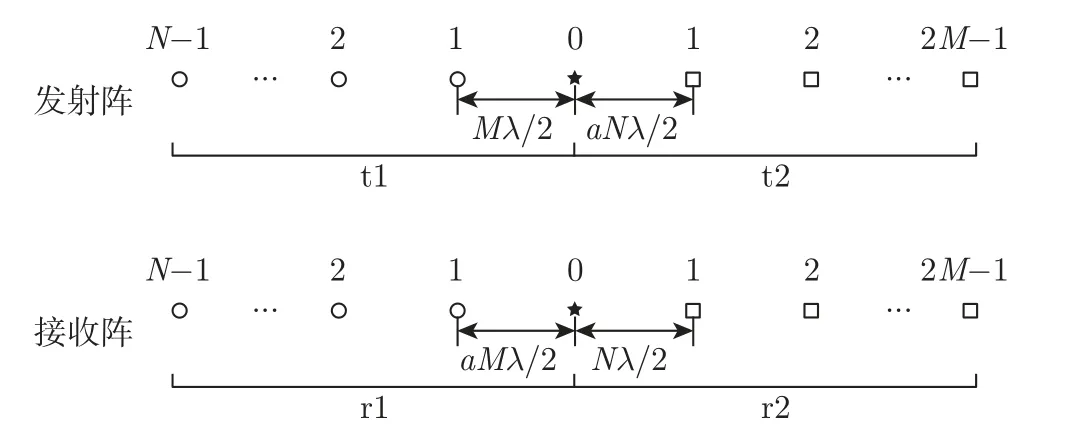
2.3 展开增广互质MIMO 雷达的自由度
3 性能分析
3.1 自由度



3.2 互耦率
3.3 克拉美罗界
4 仿真实验
4.1 空间谱
4.2 均方根误差
4.3 角度分辨力
5 结语
