干涉星敏感器测角精度影响因素的研究
2023-12-01阮宇翔
阮宇翔,董 磊
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100049)
1 引言
星敏感器是一种高精度的姿态敏感测量仪器,在航天器姿态控制系统中起着重要作用,并且在导弹制导系统、激光指向传感器系统和深空激光通信系统等方面也得到了广泛的应用[1-4]。
传统星敏感器的质心精度一般为1/10~/50像元。为了提高精度,通常会采用更小的视场。然而,更小的视场会减少用于追踪的可靠星源数量,并且降低了所需的测量速率,视场减小还会降低星敏感器的动态性能。此外,在传统的星敏感器中采用了星点质心定位技术,星敏感器的姿态测量精度随质心定位精度的提高而提高,质心定位精度的提高同时也会提高星图识别成功率[5-8]。提高星点提取精度的常用方法是采用离焦方式,即令恒星在星敏感器上的像点弥散在几个像元内,通过内插细分定位算法使星点提取精度达到亚像元甚至更高。高分辨率的焦平面阵列(FPA)可以提高传统星敏感器的质心精度。然而,当FPA 的分辨率提高时,星敏感器的重量、体积和能量损耗也会增加。此外,更高分辨率的FPA 更易于受到辐射的影响。因此,传统星敏感器的姿态测量精度与视场等因素存在制约关系,且质心定位精度存在理论上限。
传统星敏感器的上述缺陷,促使科研工作者一直在探索可规避以上问题的新型星敏感器。直到2011 年,Hutchin R A 发表了一篇干涉星敏感器的专利,利用干涉测角的方法来提高星敏感器的精度[9]。随后,美国的Optical Physics 公司(OPC)对干涉星敏感器进行了性能测试。证明干涉星敏感器在20°视场下,姿态测量精度能够达到0.11",且重量只有2 kg。该研究证实:与同视场的其他传统星敏感器相比,干涉星敏感器的姿态测量精度提高了一个数量级,真正意义上实现了大视场高精度的星敏感器。2015 年,干涉星敏感器被成功应用于美国航空航天局(NASA)的项目当中,用来开发深空激光通信光束指向应用以及为航天器导航和轨道确定提供精确的姿态测量数据。基于干涉星敏感器这项专利,国内也开展了一系列研究。浙江大学的研究团队提出了一种双轴干涉星敏感器,相较于只能提升单轴姿态测量精度的干涉星敏感器,该双轴干涉星敏感器可以同时提高两轴方向的姿态测量精度,其姿态测量精度理论上可以达到0.2"[10]。中国科学院长春光学精密机械与物理研究所(简称长春光机所)的研究团队基于Richard A.Hutchin 的专利给出的基本结构,分析了干涉星敏感器的工作原理并推导了干涉星敏感器的解析表达式[11],并通过实验验证了干涉测角技术相对于传统质心定位技术的精确性。哈尔滨工业大学的研究团队将干涉星敏感器应用于天光背景较强的近地区域(大气层内),以对目标星探测性能进行研究,完成了干涉式全天时星敏感器的光学设计[12]。
干涉星敏感器最明显的优势之一是具有极高的测角精度,虽然OPC 研究团队从理论上证明干涉星敏感器的像素细分精度可达1/1 000 像元,比传统星敏感器理论值(约1/100 像元)高约一个数量级,但是对实现该精度所付出的代价或关键技术却没有介绍。已有文献多是对工作原理或性能的理论分析,鲜有对制约其测角精度的因素和实际测角效果进行深入研究。长春光机所研究团队对常规加工和装调技术下干涉星敏感器的单星测角精度开展了初步研究。通过多次实验发现,在常规加工和装调技术下,干涉星敏感器的实际单星测角值存在较大误差,测量误差约-8"~5"[13]。这说明存在若干影响干涉星敏感器单星测角精度的因素,这些因素无法通过常规装调方法消除,故需要重点分析干涉星敏感器单星测角精度的主要影响因素,对敏感因素采用较为严格的限制措施,从而使实际测角精度达到或接近干涉星敏感器的高精度理论值。
针对干涉星敏感器实际单星测角误差较大问题,本研究团队认为需从核心原理出发寻找主要制约因素。把干涉星敏感器核心工作归结为目标光干涉条纹形成和条纹相位提取这两个环节,由此提出制约干涉星敏感器单星测角精度的两个关键科学问题:(1)干涉条纹形状对测角精度的影响机理;(2)干涉条纹的不合理分割对测角精度的影响机理。本文将围绕第二个问题开展详细的分析论证。
本文将首先介绍干涉星敏感器的基本原理;然后介绍干涉测角技术,结合干涉星敏感器的基本结构,对可能影响干涉条纹分割的因素逐一进行分析;研究这些因素对测角精度的影响程度;最后给出结论。
2 干涉星敏感器的基本原理
干涉星敏感器通过光学干涉系统提高姿态测量精度,光学干涉系统主要包括由2 个光栅组成的光栅对以及由4 个不同锲角的光锲组成的光锲阵列。干涉星敏感器的基本结构如图1 所示。探测到的星光通过第一个光栅时会产生多级衍射光,产生的±1 级衍射光通过第二个光栅时,又将产生多级衍射光。干涉星敏感器主要利用两束衍射光形成莫尔条纹,一束是利用光栅1 衍射的+1 级光经过光栅2 后再次衍射产生的-1 级光(以下简称+1/-1 衍射光),另一束是利用光栅1 衍射的-1 级光经过光栅2 后再次衍射产生的+1 级光(以下简称-1/+1 衍射光)。光栅对产生的+1/-1 衍射光和-1/+1 衍射光相互平行并且都与光轴平行。第二个光栅以光轴为转轴,旋转一个很小的角度,这就在光栅对之间引入一个旋转角,并且第二个光栅放置在第一个光栅的泰伯距离处,从而可以产生莫尔条纹。莫尔条纹相位与入射光的角度存在一一对应关系,而干涉星敏感器可以精确测量莫尔条纹相位,从而实现对目标光入射角的精确测量。莫尔条纹相位测量主要通过光锲阵列、成像光学系统和相机实现。光楔阵列将一个周期的干涉条纹平均分成了4 个部分,4 个部分的光波经过成像光学系统后,最后在相机平面上形成4 个独立可区分的光斑。再利用成熟的ABCD 方法[14-17],即可实现对莫尔条纹相位的精确估计。
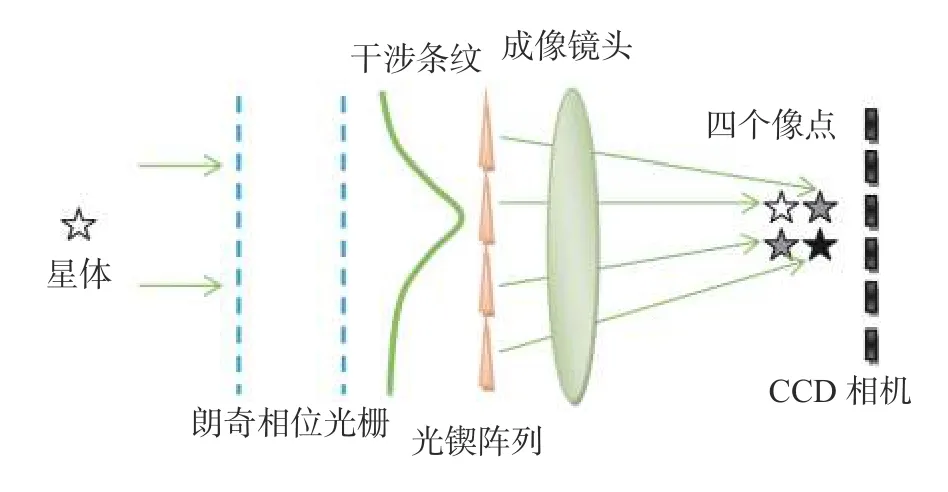
图1 干涉星敏感器系统的基本结构Fig.1 The basic structure of the interferometer start tacker system
3 干涉测角技术的测角精度及其条纹分割误差
干涉测角技术的莫尔条纹相位与目标光入射角之间存在近似线性关系[18]。通过对干涉星敏感器系统所形成的干涉条纹相位进行精确估计,并经过简单计算,即可获得目标光入射角的精确估计。下面将介绍干涉测角技术实现精确的角度测量的具体方法。入射目标光经过光栅对将在光楔阵列表面形成莫尔条纹(理想的条纹是正弦函数形状),调节光栅对的相对轴向转角,使其在光楔阵列范围内产生一个周期的条纹结构。光楔阵列对一个条纹周期的4 个不同区域进行分割并引入不同方向的偏转,再经过光学成像系统在探测器靶面上形成4 个独立可区分的光斑(如图2 所示[19])。这4 个光斑的光强值对应一个周期条纹在4 个等分区间内的积分值。图2 中,每一幅图里由箭头标记的光斑有最大的强度,即为最亮的光斑。由图2 可知,在某些特定的角度下只能看到3 个光斑,这是因为光斑强度随目标光入射角呈正弦规律变化,在某些特定角度下某个光斑的光强值为零。最亮光斑的位置在4 个点之间旋转变化,实际上最亮光斑的旋转方向取决于目标光与干涉星敏感器之间的相对运动,沿同一个方向相对运动将产生顺时针旋转,而沿相反方向的相对运动将产生逆时针旋转。

图2 单颗星在探测器平面上的光斑强度分布Fig.2 The spot intensity distribution of a single star on the plane of the detector
下面将结合相关数学公式给出计算干涉星敏感器测角精度的数学模型。根据ABCD 表达式,由4 个光斑的光强值可得出莫尔条纹的相位值,如式(1)所示:
式(1)中,φ表示莫尔条纹的相位,I1,I2,I3,I4分别表示4 个光斑的光强值(即分别代表A值、B值、C值、D值)。图2 中第一幅图指针所示为I1,I1右边是I2,I1下边是I3,I3右边是I4。后面的图则给出了光斑亮度周期性变化的分布结果。最后,根据目标光入射角与条纹相位之间的对应关系精确计算目标光的入射角:
式(2)中,θ表示入射角,p表示光栅周期,d表示光栅对之间的间距。干涉星敏感器系统的测角精度ε可以表示为:
式(3)中,M表示通过插值技术可获取的一个周期条纹的相位细分数。由式(3)可以看出,光栅周期p越大,干涉探测系统的测角精度 ε越低;光栅对之间的间距d和相位细分数M越大,干涉探测系统的测角精度 ε越高。
当然前面给出的干涉测角技术的原理公式是在理想情况下推导出来的结果。实验过程中测量角度与转台角度间存在偏差,即为测量误差,转台在不同角度下的测量误差如图3 所示。由图3 可以看出,受实际加工和装调误差的影响,干涉星敏感器本身就存在一些影响测角精度的因素,需要对这些因素进行定量分析,从而便于对影响较大的因素采取措施进行抑制,使干涉星敏感器的实际测角精度接近理论精度。在引言中提到主要有两个关键问题制约干涉星敏感器的测角精度,本文主要分析第二个关键问题,即干涉条纹的分割误差对测角精度的影响机理。下面我们将针对该问题进行深入的分析。
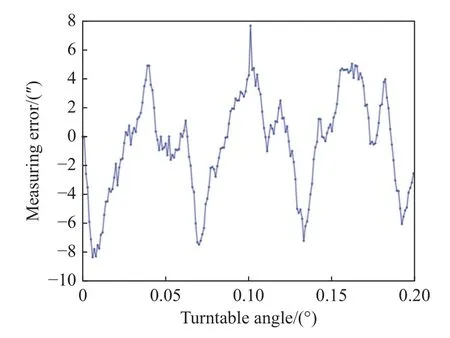
图3 实验测量误差随转台角度的变化Fig.3 Experimental measurement error varying with turnable angle
干涉测角技术采用ABCD 方法估计条纹相位,为了避免引入误差,需要对两个光栅所形成的一个周期的莫尔条纹在垂直条纹方向进行严格的四等分。然而,实际上莫尔条纹的周期和取向均会与光楔阵列的整体通光尺寸和排列方向存在差异性,另外由于存在加工和装调误差,4 个光楔也存在不等分的情况,上述因素会造成一个周期的干涉条纹出现分割误差,从而降低条纹相位估计精度。综上可知,干涉条纹的分割误差可分成以下3 种情况:(1)光楔阵列不等分;(2)莫尔条纹周期与光楔阵列整体通光尺寸不匹配;(3)莫尔条纹取向与光楔阵列排布方向不正交。下面我们将对这3 种情况以及解决方案进行详细的介绍。
3.1 光楔阵列不等分
每个光楔都存在加工误差,尺寸不会完全相等。也就是说4 个光楔在垂直条纹取向方向的宽度不相等,如此一来在相机靶面上获得的4 个光强值与条纹四等分情况将存在差异,代入式(1)后得到的相位值也将存在差异,从而影响干涉测角技术的测角精度。对于该误差对条纹相位估计的影响可采用以下方法进行研究。
假设覆盖在光楔阵列前表面的干涉条纹是单色平面波产生的理想正弦条纹,并且满足以下两个条件:(1)条纹取向严格垂直于光楔阵列的排布方向;(2)莫尔条纹周期与光楔阵列整体通光尺寸相等。这时光楔阵列不等分问题可利用正弦函数一个周期内所包围面积的不等分来描述。
如图4 所示,将一个周期正弦函数分成4 个区间。每个区间内正弦函数曲线下所包围的面积值即为ABCD 方法中4 个数值(A值、B值、C值或D值)之一,然后将上述4 个数值代入ABCD 方法对应的计算公式,可获得4 个区间不等分对条纹相位的影响情况,再代入条纹相位与测角精度的关系式即可得到对测角精度的影响。在上述的分析中可选择不等分区间宽度与四等分宽度相对偏差的上限,例如1%,5%,10%等,再令前3 个不等分区间宽度等于四等分区间宽度再加上一个随机变量(上限在前面给出),最后一个不等分区间宽度等于一个干涉条纹的周期减去前三个区间宽度之和。
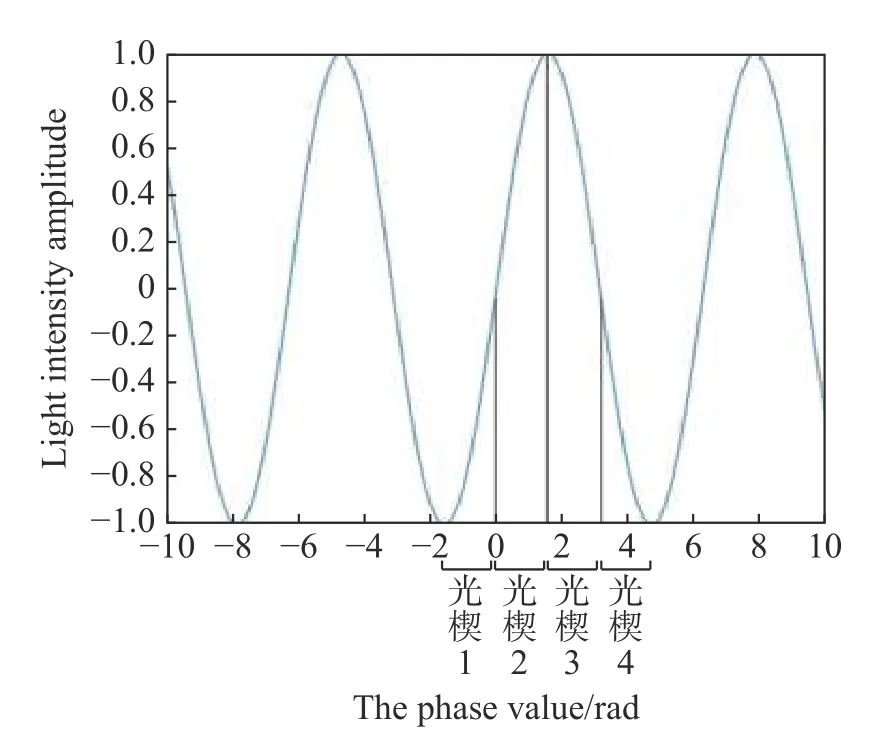
图4 一个周期正弦函数的区间分割Fig.4 Interval segmentation of the sine function in one period
3.2 莫尔条纹周期与光楔阵列整体通光尺寸不匹配
实际莫尔条纹周期由两个光栅沿光轴方向的相对旋转产生,而光楔阵列整体通光尺寸取决于加工和装调工艺,一旦装好,光楔阵列的尺寸就是定值,这时只能通过调节莫尔条纹周期使其与光楔阵列尺寸相等。然而,对准过程必然存在误差。对于该误差对条纹相位估计的影响可采用以下方法进行研究。
假设覆盖在光楔阵列前表面的干涉条纹是单色平面波产生的理想正弦条纹,并且满足以下两个条件:(1)条纹取向严格垂直于光楔阵列的排布方向;(2)光楔阵列四等分。这时莫尔条纹周期与光楔阵列整体通光尺寸不匹配问题可用正弦函数一个周期内所包围面积的不完全分割(欠分割)或过量分割(过分割)来描述。
图5 为不同分割方式对应的整体分割宽度,即光楔阵列的整体通光尺寸。将分割宽度四等分,每个等分区间内正弦函数曲线下所包围的面积值即为ABCD 方法中4 个数值(A值、B值、C值或D值)之一,然后将上述4 个数值代入ABCD 方法对应的计算公式,可分别获得正分割、欠分割和过分割对应的条纹相位估计值。由此得出欠分割和过分割对条纹相位的影响情况。再代入条纹相位与测角精度的关系式即可获得对测角精度的影响。在上述分析中可选择不同分割宽度与正分割的相对偏离量,例如1%,5%,10%等。
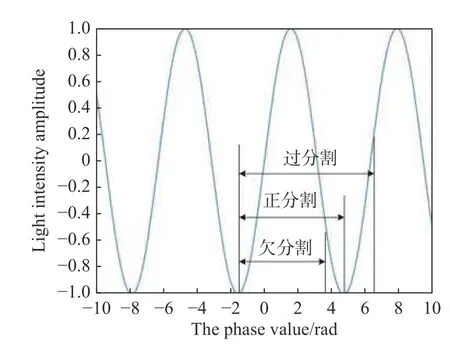
图5 一个周期正弦函数的分割方式Fig.5 The segmentation type of the sine function in one period
3.3 莫尔条纹取向与光楔阵列排布方向不正交
本方案假设水平取向的条纹周期等于光楔阵列整体通光尺寸且光楔阵列将一个条纹周期四等分。水平取向的正弦条纹在一个周期内的光强分布,如图6 所示。将条纹旋转一定角度可获得倾斜条纹结构,如图7 所示。水平条纹和倾斜条纹在不同位置竖直切面内的光强分布如图8 所示。由图8 可知,倾斜条纹的中心竖直切面内条纹周期比水平条纹偏大,这将引起条纹相位估计误差。另外,倾斜条纹不同位置处的竖直切面内的条纹相位也不同,利用ABCD 方法获得的整体条纹相位可认为是不同切面内相位的平均效果,也将引入相位估计误差。

图6 水平条纹的光强分布Fig.6 The light intensity distribution of the horizontal fringe

图7 倾斜条纹的光强分布Fig.7 The light intensity distribution of the oblique fringe
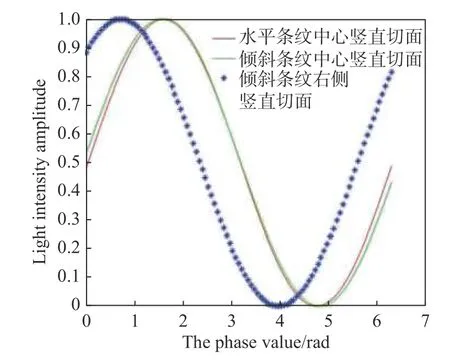
图8 水平条纹和倾斜条纹在不同位置竖直切面内的光强分布Fig.8 The light intensity distributions of the horizontal and oblique fringes in the vertical section at different positions
基于水平条纹的中心竖直切面中的函数结构(如图8(彩图见期刊电子版)中红线所示),计算函数曲线在光楔阵列每个四等分区间内的面积值(即A值、B值、C值或D值),利用ABCD 方法计算该函数曲线的相位。因条纹取向水平,故任意竖直切面内条纹相位均相等,即该函数曲线的相位代表了水平条纹的相位。
对于倾斜条纹来说,不同位置处竖直切面内条纹相位不同(如图8 中绿线和蓝星线所示),故将光楔阵列四等分区间的第一个区间所对应的倾斜条纹所有竖直切面内函数曲线面积求和作为A值,同样方法计算第二个区间作为B值,然后再获得C值和D值。利用ABCD 方法计算倾斜条纹的相位。该相位与水平条纹相位的差值即为相位误差,代入条纹相位与测角精度之间的关系式可获得其对测角精度的影响。研究不同条纹倾斜角对条纹相位估值的影响,进而获得对测角精度的影响。
前面介绍了干涉条纹的分割误差可能出现的3 种情况,并给出研究方案,下面将按照上述方案对以上3 个影响因素进行研究分析。
4 条纹分割误差对干涉星敏感器精度影响的研究分析
为了便于分析,取光栅周期p=50 μm,光栅对之间的间距d=5 cm,相位细分数M=1 024,将以上数据代入式(3)中,可以得到测角精度为 ε为0.1"。0.1"就是期望达到的理想值。下面分别对光楔阵列不等分误差、莫尔条纹周期与光楔阵列整体通光尺寸不匹配误差以及莫尔条纹取向与光楔阵列排布方向不正交误差这3 种情况开展研究分析,给出这3 个因素对干涉测角精度的定量影响结果。
4.1 光楔阵列不等分误差的影响分析
光楔阵列的加工公差一般为1%,较严格的加工公差可以达到0.5%,更为精细的加工公差可以达到0.2%。因此,在对光楔阵列不等分误差进行研究时,选取了0.1%~1%的误差范围进行分析。图9 给出了0.1%~1%的误差范围所产生的测角误差。可以看到测角误差随光锲阵列不等分误差的增大而增大,光楔阵列不等分误差为1%时,测角误差达到最大值,为0.004 5"与理想值0.1"还相差两个数量级,完全可以忽略不计。因此,光锲阵列不等分误差显然不是影响干涉测角技术精度的因素。
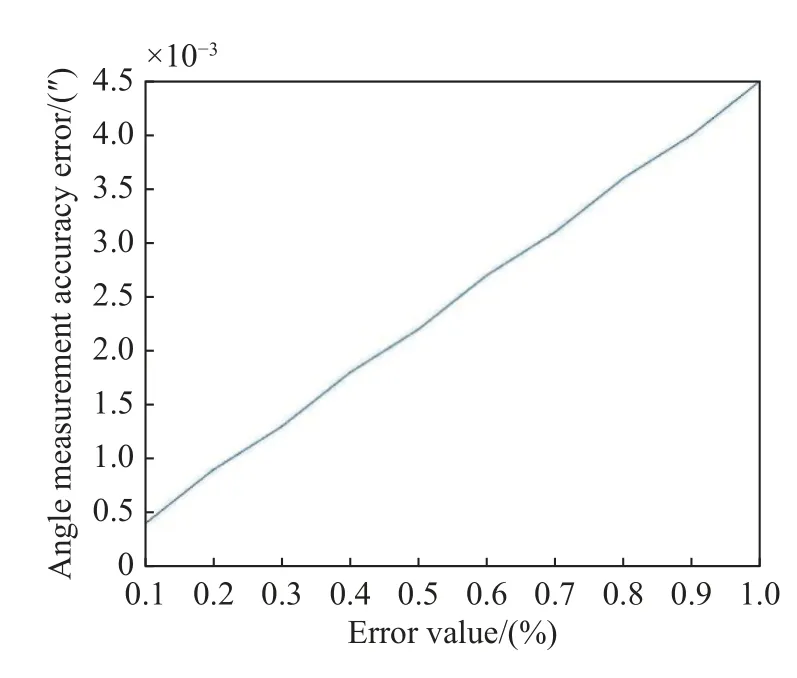
图9 光楔阵列不等分误差Fig.9 Optical wedge array unequal division error
4.2 莫尔条纹周期与光楔阵列整体通光尺寸不匹配误差的影响分析
由第2 部分的分析可知,莫尔条纹周期与光楔阵列整体通光尺寸不匹配误差分为两种情况。图10 是欠分割误差与过分割误差的结果,实线表示的是欠分割误差的结果,虚线表示的是过分割误差的结果。结合实际情况,莫尔条纹周期与光楔阵列整体通光尺寸不匹配误差应当不超过10%,因此,选取了1%到10%的误差范围进行分析。由图10 可以看出,不论是欠分割误差还是过分割误差,测角误差都会随之增大而增大。此外,过分割时测角误差增长的速度比欠分割时增长的速度更快,也就是说过分割时,测角误差累积得更快。第4 节刚开始给出了干涉测角技术的主要模拟参数,可算出综合测角精度的理论值为0.1"。为了使实际综合测角精度接近上述理论值,单因素引起的测角误差应小于理论值的1/10,因此莫尔条纹周期与光楔阵列整体通光尺寸不匹配引起的测角误差应小于0.01"。欠分割误差为1%时,测角误差为0.009";过分割误差为1%时,测角误差为0.009"。因此,莫尔条纹周期与光楔阵列整体通光尺寸不匹配误差小于1%可保证单因素测角误差小于0.01"。这就对莫尔条纹周期与光楔阵列整体通光尺寸的匹配情况提出较为严格的要求。
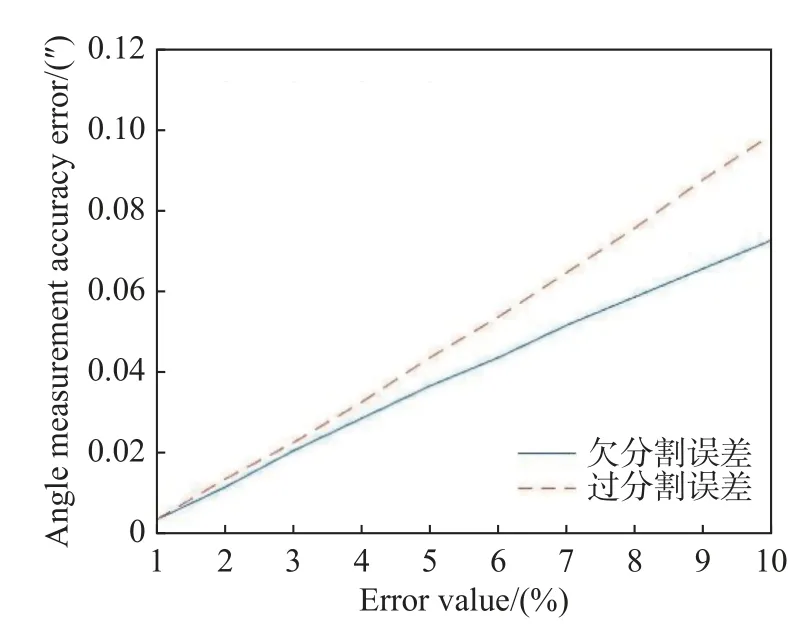
图10 欠分割与过分割误差Fig.10 Under segmentation and over segmentation errors
4.3 莫尔条纹取向与光楔阵列排布方向不正交误差的影响分析
图11 是莫尔条纹取向与光楔阵列排布方向不正交误差的研究分析结果。条纹旋转角度的范围为1°~10°。从图11 可以看出,随着干涉条纹旋转角度增大,测角精度的误差先增大后减小。当条纹旋转角度从3°变化到4°时,测角误差有一个突变,使测角误差陡然增大。测角误差最小为0.066",对应条纹旋转角度为1°。但是仍大于可接受的测角误差(0.01")。因此,将条纹旋转角度进一步细分,取0.1°到1°的范围进行分析,如图12 所示。当条纹旋转角度从0.1°变化到1°时,测角精度的误差总体来说是逐渐增大的,但是测角误差出现了3 组相同的数据,条纹旋转角度为0.2°和0.3°、0.4°和0.5°以及0.6°和0.7°时,测角误差完全相同。当条纹旋转角度为0.1°时,测角误差为0.006",符合理想误差值。因此,条纹旋转角度应当小于0.1°,此时通过人眼已经无法分辨如此小的角度,可以通过相机进行分辨。

图11 莫尔条纹取向与光楔阵列排布方向不正交误差Fig.11 Nonorthogonal error between the orientation of the Moire fringe and the orientation of the optical wedge array
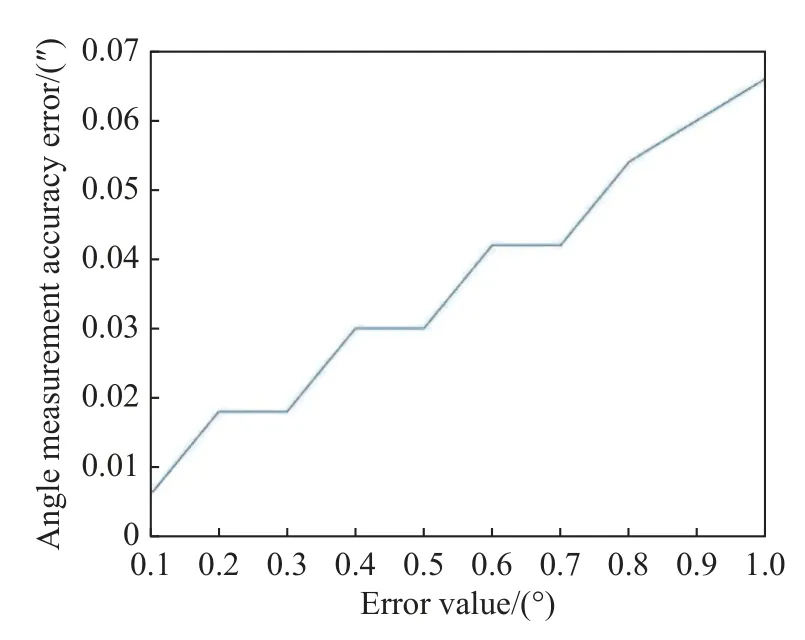
图12 莫尔条纹取向与光楔阵列排布方向不正交误差(细分)Fig.12 Nonorthogonal error between the orientation of the Moire fringe and the orientation of the optical wedge array (subdivision)
5 结论
本文针对干涉星敏感器存在的若干影响其单星测角精度的因素展开研究。首先,介绍了干涉星敏感器的基本原理。然后,介绍了干涉测角技术,并将干涉条纹的分割误差问题分解为3 种情况:(1)光楔阵列不等分误差;(2)莫尔条纹周期与光楔阵列整体通光尺寸不匹配误差;(3)莫尔条纹取向与光楔阵列排布方向不正交误差。最后,分别对上述3 种影响干涉星敏感器测角精度的因素展开分析,获得其对测角精度的定量影响结果。
研究结果证明:莫尔条纹周期与光楔阵列整体通光尺寸不匹配误差小于1%时,可保证单因素测角误差小于0.01";对于莫尔条纹取向与光楔阵列排布方向不正交误差,条纹旋转角度应当小于0.1°,可保证单因素测角误差小于0.01"。
