惯性传感器地面弱力测量系统热设计
2023-12-01任丽敏陈立恒
任丽敏,陈立恒 ,孟 旭,王 智
(1.中国科学院长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100049;3.中国科学院大学材料与光电研究中心,北京 100049;4.中国科学院大学 杭州高等研究院 基础物理与数学科学学院,杭州 310024)
1 引言
空间引力波探测“太极计划”[1-2]是由中国科学院牵头提出的空间激光干涉引力波探测计划,旨在探测频率为0.1 mHz~1 Hz 的引力波信号[3]。惯性传感器地面弱力测量试验是中国空间引力波探测“太极计划”发展规划中的重要任务之一,其目的是通过在地面实验室环境中搭建超高温度稳定性热环境,以满足惯性传感器敏感结构的温度稳定性需求,验证空间惯性传感器的在轨工作性能。在引力波探测的低频领域(毫赫兹及以下),温度噪声能以多种方式影响惯性传感器的探测灵敏度。温度及温度梯度波动产生的温度噪声可能会淹没被测信号。为了保证惯性传感器的探测灵敏度,理论分析认为,在0.1 mHz~1 Hz 的测量频带内,“太极3 号”卫星惯性传感器敏感结构的温度稳定性要求优于10-5K/Hz1/2。因此,在惯性传感器地面试验中需要对测量系统进行热设计,以保护惯性传感器地面弱力测量试验不受温度噪声的影响[4]。
目前,国内外已有较多有关精密热控制的相关研究。在“LISA 探路者”卫星热诊断系统的地面测试中,Lobo 等人提出了“绝热体”系统概念。该系统可在实验室环境下实现10-6K/Hz1/2的温度稳定性[5]。Higuchi 等人研发了一种用于模块化重力参考传感器(MGRS)地面验证测试的热测试设备,在0.1 mHz~0.1 Hz 频段内,该设备可提供优于30 μK/Hz1/2的热稳定性[6]。“天琴1 号”卫星核心载荷区域采用高精度铂电阻温度传感器和精密的热设计,实现了每轨±3 mK 的温度稳定性[7]。“太极1 号”卫星采用了“恒温笼”的热控制策略以及三级控温方式,实现了卫星核心区域在轨飞行±5 mK/1 000 s 的温度稳定性[8-9]。
当前,针对地面试验的高精度、高稳定性温度控制国外研究较多,国内大多以空间相机和空间载荷为主,相关研究较少。针对空间惯性传感器地面弱力测量系统体积庞大,难以实现高精度、高稳定性热控制这一问题,本文根据惯性传感器地面弱力测量系统所处热环境及内部热功耗情况,结合国内外相关研究成果,对其进行了详细的热设计。然后,根据环境基准温度水平定义了两种热分析工况,对整体结构进行了热仿真分析。最后,通过热仿真分析结果验证了热设计的合理性。
2 惯性传感器地面弱力测量系统概述
2.1 系统组成
空间惯性传感器在轨工作时,其核心部件测试质量(TM)在空间微重力环境下始终保持自由落体状态。在地面试验中,由于受到重力和大地脉动的影响,导致惯性传感器无法完全正常工作。同时,空间惯性传感器分辨率非常高,量程又远小于重力加速度[10],因此采用了悬丝扭秤系统来抑制地球重力对测量的影响。惯性传感器地面弱力测量系统结构如图1 所示,测量系统整体安装在结构尺寸为Φ2 500 ×3 800 mm 的立式圆柱体环境模拟器中,整个试验过程均在真空环境下进行。
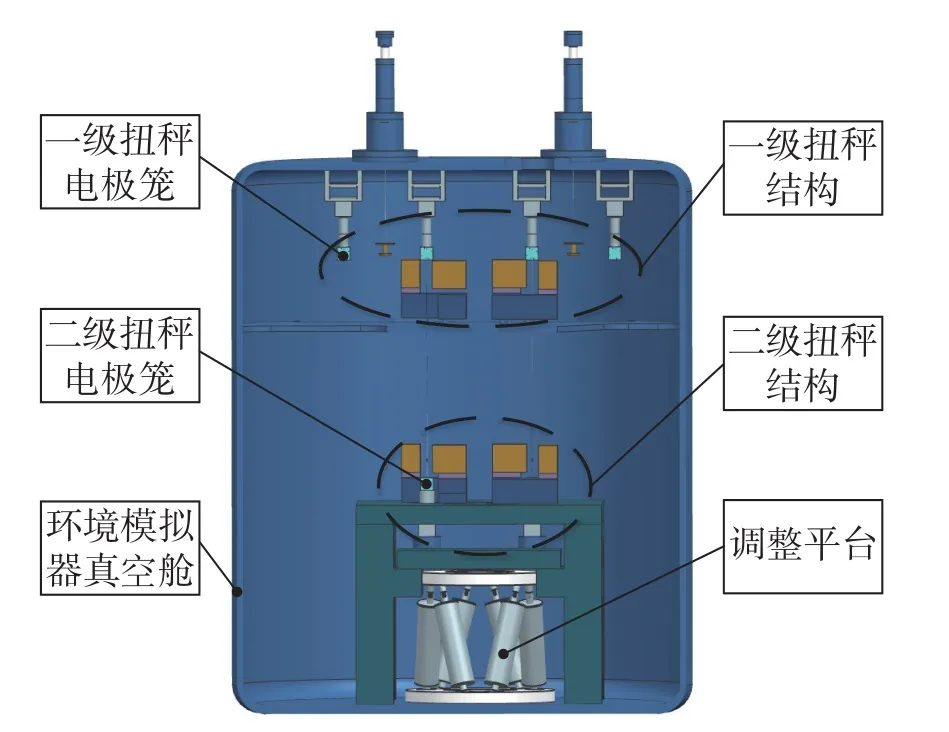
图1 惯性传感器地面弱力测量系统结构Fig.1 Overall structure of the ground weak force measurement system for inertial sensor
测量系统主要由一级扭秤结构、二级扭秤结构、五自由度调整平台等部分组成。其敏感结构主要包括一级扭秤电极笼、二级扭秤电极笼及光学干涉仪平台。环境模拟器系统主要包括真空舱、分子泵、离子泵等。
2.2 热环境分析
为了减少环境扰动对惯性传感器地面弱力测量系统的干扰,在地下10 m 的密闭实验室环境中对测量系统及环境模拟器进行地面测试。
弱力测量试验中影响弱力测量系统温度稳定性的因素主要包括实验室环境温度的波动、内部热源的发热。密闭实验室将为测量系统提供(289.15±0.5) K~(293.15±0.5) K 的环境温度边界,测量系统及热控结构的内部热源主要包括:离子泵、分子泵和五自由度调整平台,各部分内热源的发热功耗如表1 所示,离子泵和分子泵在地面试验过程中持续工作,五自由度调整平台仅在最初1 小时内进行工作。
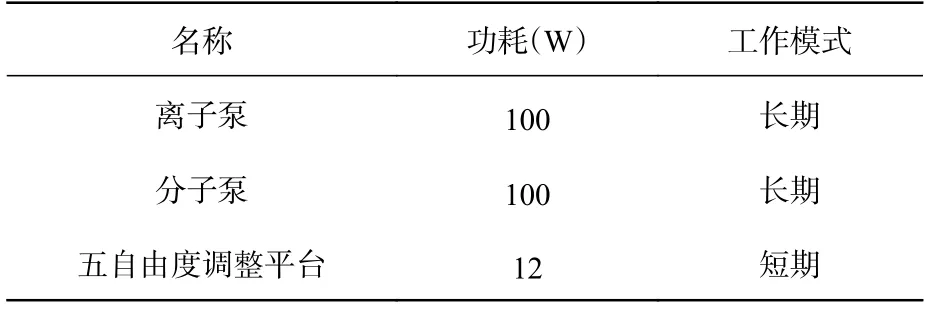
表1 测量系统内各热源发热功耗Tab.1 Thermal power consumptions of heat sources in measuring system
图2 为测量系统敏感结构传热路径示意图,其描绘了实验室热环境及内部热源与测量系统敏感结构之间的传热路径。实验室热环境与隔热层、隔热层与真空舱之间通过空气自然对流、热辐射及热传导等方式进行热量交换,而真空舱与测量系统组件及测量系统组件间的热交换方式仅包括热辐射及热传导。
3 惯性传感器地面弱力测量系统热设计
在真空试验环境中,测试质量(TM)周围的温差波动会产生辐射计效应、辐射压力效应、不对称出气效应[11]等温度效应。这些温度效应产生的热噪声是影响惯性传感器测量灵敏度的重要干扰源。
为了满足惯性传感器的测量灵敏度需求,热控设计指标要求惯性传感器地面弱力测量系统敏感结构工作基准温度为(293.15± 0.5)K。试验过程中,在0.1 mHz~1 Hz 目标频段内,要求测量系统的敏感结构温度稳定性优于10-4K/Hz1/2。
在密闭实验室环境中,环境的热噪声以高斯白噪声形式作为温度边界输入。为了降低环境温度噪声和内热源对测量系统温度稳定性的影响,采用了“主动热控和被动热控相结合”的热控制方法,对测量系统进行整体热设计,提出针对惯性传感器地面弱力测量系统的详细热控方案,以满足热设计指标需求。
3.1 被动热控系统设计
测量系统的热控模型如图3 所示。为了满足惯性传感器地面弱力测量系统高精度、高稳定性的热控需求,采用了“三级热控”结构进行整体热设计。其中:一级热控结构为密闭实验室;二级热控结构为铝蜂窝板和聚苯乙烯板组成的隔热层;三级热控结构为环境模拟系统真空舱。
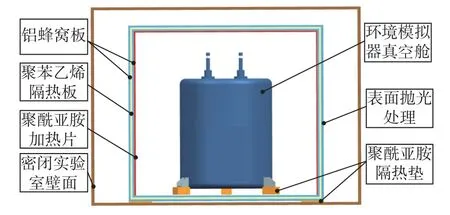
图3 惯性传感器地面弱力测量系统热控结构示意图Fig.3 Schematic diagram of the thermal control structure of the ground weak force measurement system for inertial sensor
3.1.1 一级热控结构
密闭实验室长、宽、高分别为7 000 mm、7 000 mm、5 000 mm。实验室温控系统将为整个实验室环境提供289.15~293.15 K 的温度边界,同时环境温度波动值小于等于±0.5 K。实验室温控系统将隔绝外部环境的温度波动。同时,密闭环境将抑制空气流动,减少二级热控结构与环境的对流换热,进一步降低测量系统整体温度波动。
3.1.2 二级热控结构
二级热控结构由复合多层结构组成:内、外两层由厚度为25 mm 的航空铝蜂窝板组成,中间夹层为25 mm 厚的聚苯乙烯泡沫板,三层结构通过胶接方式复合形成一个整体热隔离层,同时,在隔热板连接处进行涂胶密封处理。铝蜂窝板不仅保证了隔热层的结构刚度,而且与板材相比,蜂窝状结构可以更好地使环境温度波动衰减。在此基础上,聚苯乙烯泡沫层进一步降低温度波动水平,尤其是在较低频率范围内,聚苯乙烯材料具有更强的隔热效果。隔热层整体外部结构轮廓尺寸为:5 000 mm×5 000 mm×4 300 mm,隔热层与实验室地面采用了4 个小平面进行隔热安装,安装平面之间增加了20 mm 厚聚酰亚胺隔热垫,并采用钛合金螺栓进行固定,以减少二级热控结构与实验室地面之间的热传导。同时对二级热控结构外层铝蜂窝板外表面做抛光处理,保持红外发射率ε≤0.1,减少二级热控结构与实验室环境的辐射换热,进一步降低环境温度波动对测量系统温度稳定性的影响。
3.1.3 三级热控结构
三级热控结构(空间环境模拟器真空舱)为Φ 2 500×3 800 mm 的圆柱形不锈钢真空罐,其壁厚为32 mm。真空舱内部热沉表面涂覆黑漆以增大其红外发射率,同时真空舱自身较大的热容也会进一步减小温度波动,进而为测量系统提供更好的温度均匀性。真空舱采用“三点式”安装方式,利用钛合金螺栓直接与实验室地面安装平台进行固定安装,真空舱与安装平台之间采用200 mm厚度的聚酰亚胺隔热垫隔热安装,以减少真空舱与安装平台之间的传导换热。环境模拟器配套设备分子泵和离子泵具有较大的长期发热功耗,为了避免其对测量系统温度水平与温度稳定性的影响,采用恒温水槽对分子泵和离子泵进行水冷散热,保证泵体基准温度为293.15 K,泵体温度波动水平小于等于0.1 K。
3.1.4 测量系统热控
在试验过程中,测量系统组件处于真空状态,其与真空舱的热交换方式为热传导和热辐射。测量系统一级扭秤电极笼通过悬挂支架、六自由度调整机构及调整架过渡板与真空舱进行传导换热。一级扭秤电极笼与测量系统中的可视组件及真空舱进行辐射换热。一级扭秤悬挂支架与真空舱之间采用10 mm 厚度聚酰亚胺隔热垫隔热安装,同时采用钛合金螺栓进行固定,以隔绝真空舱与一级扭秤敏感结构之间的热传导。五自由度调整台与弱力测量支撑平台之间同样采用聚酰亚胺隔热垫进行隔热安装,以减少二级扭秤敏感结构与真空舱的热传导,最大限度减少环境温度波动对测量系统温度稳定性的影响。五自由度调整台工作时间较短且功耗较小,测量系统的整体温度水平将保持在可接受范围内。惯性传感器地面弱力测量系统热控结构及测量系统部分结构材料选择如表2 所示。
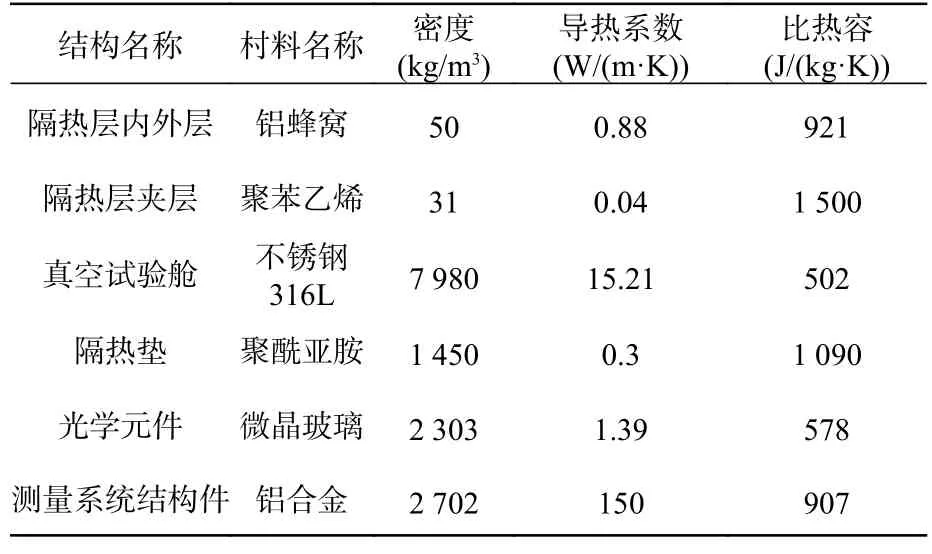
表2 热控结构及测量系统部分结构材料表Tab.2 List of structural materials of thermal control structure and measuring system
3.2 主动热控系统设计
惯性传感器地面弱力测量系统的目标工作温度为293.15 K,温度稳定性要求为10-4K/Hz1/2。密闭实验室环境的基准温度水平为289.15~293.15 K。当惯性传感器地面弱力测量系统温度水平低于293.15 K 时,需采用主动加热方式进行温度补偿,使其基准温度达到目标温度。同时由于实验室温控系统的控温精度有限,在低频范围内,特别是在频率远低于0.1 mHz 的情况下,被动热控措施的热隔离效果将明显变差,因此,需要采用主动热控制系统提高测量系统整体控温精度[12]。
3.2.1 主动热控措施
采用上文提到的主动热控措施,在二级热控结构隔热层内表面的侧面与顶面进行主动加热补偿。考虑主动加热回路的加热面积较大,且温度均匀性要求较高,因此选用片状聚酰亚胺薄膜型电加热器对二级热控结构进行分区加热。运用比例积分微分(PID)控制算法,通过控制各加热回路的电压来调节加热片的加热功率,对二级热控结构内层铝蜂窝板的温度波动进行快速细微调控,使其基准温度满足测量系统的目标温度需求,同时降低环境温度波动水平。
对二级热控结构建立温度变化模型,当主动加热回路不工作时,第二级热控结构内表面温度变化曲线为:
其中,Tnoise表示环境噪声。
在该试验方案中,通过简化传热模型,得到单位时间温度增量ΔT与加热片输入电压之间的关系:
其中:ΔT为单位时间内二级热控结构温度增量;U为加热片加热回路电压(变量);R为加热片电阻;cp1为二级热控结构材料的比热容;cp2为加热片比热容;m1为二级热控结构质量;m2为加热片质量;95%为热仿真中的设定参数,为考虑热量耗散后用于地面弱力测量系统加热升温的热量比例。
由此可得,二级热控结构内层温度随时间的变化关系为:
3.2.2 PID 控制算法
温度控制具有大惯性、大时滞、参数时变、过程非线性等特点,传统的温控方法难以满足如此高精度的控温需求。本文采用PID 控制算法。PID 控制算法的控温原理如图4 所示。
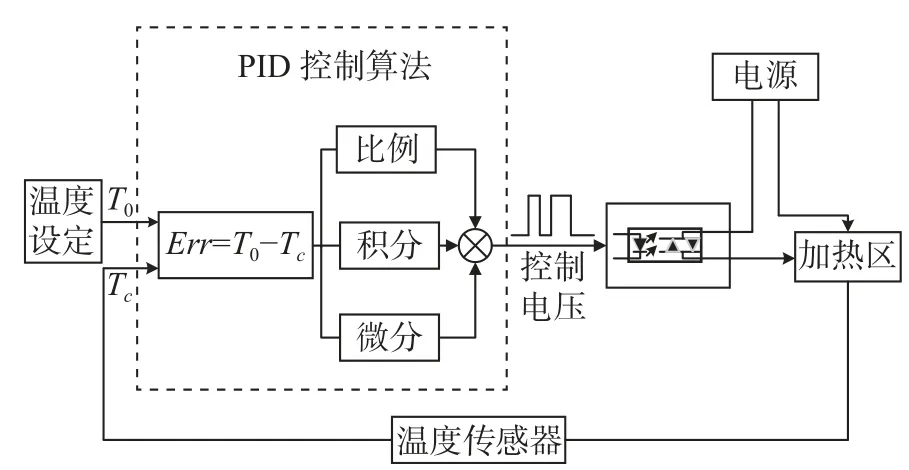
图4 PID 控制原理图Fig.4 Schematic diagram of PID control principle
在对惯性传感器地面弱力测量系统进行主动热控制时,采用位置式PID 控制算法。控制系统直接输出控制量,控制系统的原理可表示为[13-15]:
式中:Kp是比例系数;TI是积分常量;TD是微分时间常数;Ts是采样时间;e(t)是t时刻设定温度与实际测量温度的差值;T0是被控对象的目标温度;Tc是被控对象实际测量温度;u(t)是t时刻主动补偿加热功耗。
在惯性传感器地面弱力测量系统主动热控回路中,采用功率限幅设计,当控制量u(t)大于功率限幅时,则u(t)以功率限幅值输出,当u(t)˂0 时,则取u(t)=0。
PID 控制算法的参数整定是通过调整控制器的参数Kp、TI、TD,使得控制回路的动态特性满足温度控制指标要求,以达到理想的控制目标。本文采用了试凑法对PID 控制算法进行参数整定,通过观察过程曲线的变化修改参数,直到获得理想的控制回路的动态特性[14]。试凑时一般根据各参数的特点,对参数实行先比例、后积分、再微分的步骤进行整定,最终选取PID 控制参数Kp=50,TI=0.001,TD=150。
4 热控系统仿真分析
为了验证惯性传感器地面弱力测量系统热设计的正确性与合理性,采用有限元分析法(FEA)对测量系统和热控结构进行热仿真分析。根据仿真结果,不断优化和调整热控方案,以实现最佳热设计方案。
4.1 热分析模型
在本研究中,利用UG/NX 有限元分析软件建立了测量系统与热控结构的整体热分析模型,如图5 所示。
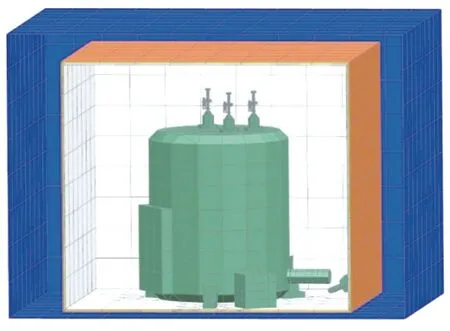
图5 惯性传感器地面弱力测量系统有限元模型Fig.5 Finite element model of the ground weak force measurement system for inertial sensor
为了提高热分析效率,在不影响传热路径的情况下对热分析模型进行了如下简化:
(1) 对薄壁结构的组件使用壳体单体进行简化,单元厚度按照体积等效厚度计算;模型共划分了32 762 个单元。
(2) 在建模过程中,采用热耦合简化了部件之间的热传导,热分析模型中共建立了74 个热耦合。
根据能量守恒定律,建立了集总参数模型,惯性传感器地面弱力测量系统热平衡方程:
其中:Q为系统的内部能量增量;Qcv为对流换热量;Qcd为传导换热量;Qr为辐射换热量;Qh为内热源产生的热量;其单位均为W。整体结构热分析模型由一系列的单元和节点组成。假设热模型单元的质量和热容量集中在单元节点上,则任意节点i的热平衡方程可以表示为:
其中:Cp,i和mi表示节点i的比热容和质量;Qe,i表示节点i与环境的热量交换:Qi表示节点i自身产生的热量;Dij表示节点i与节点j之间的传导换热系数;Eij表示节点i与节点j之间的辐射换热系数;Ti,Tj分别表示节点i,j的温度;m,n分别表示与节点i进行传导换热和辐射换热的节点数量。节点i与环境的热量交换可以表示为:
其中:σ为斯特藩-玻耳兹曼(Steven-Boltzmann)常数;F表示辐射角系数;ε、Ai、ΔTi分别表示节点i的红外发射率、表面积和节点与环境的温度差;h表示对流换热系数。
4.2 热分析工况
测量系统敏感结构的温度稳定性主要受密闭实验室环境温度、内热源以及主动热控加热回路的影响,同时实验室环境的空气对流换热强度、各级热控结构表面的热属性等因素都将对其造成影响。
热仿真考虑实验室环境温度边界的两种极端情况,将实验室基准温度为289.15 K 和293.15 K时分别定义为低温工况和高温工况。同时为了验证主动热控系统的有效性,对高温工况无主动热控措施下的弱力测量系统进行了热仿真分析。实验室环境温度边界以高斯白噪声形式作为输入,噪声曲线在每一采样点处的温度值均服从高斯分布,其温度均值μ为密闭实验室基准温度,其标准差σ≤0.5/3,即保证实验室温度边界的温度值分布在(μ-0.5,μ+0.5)中的概率为99.74%,图6(a)、6(b)(彩图见期刊电子版)分别表示高温工况和低温工况时实验室的温度边界曲线。
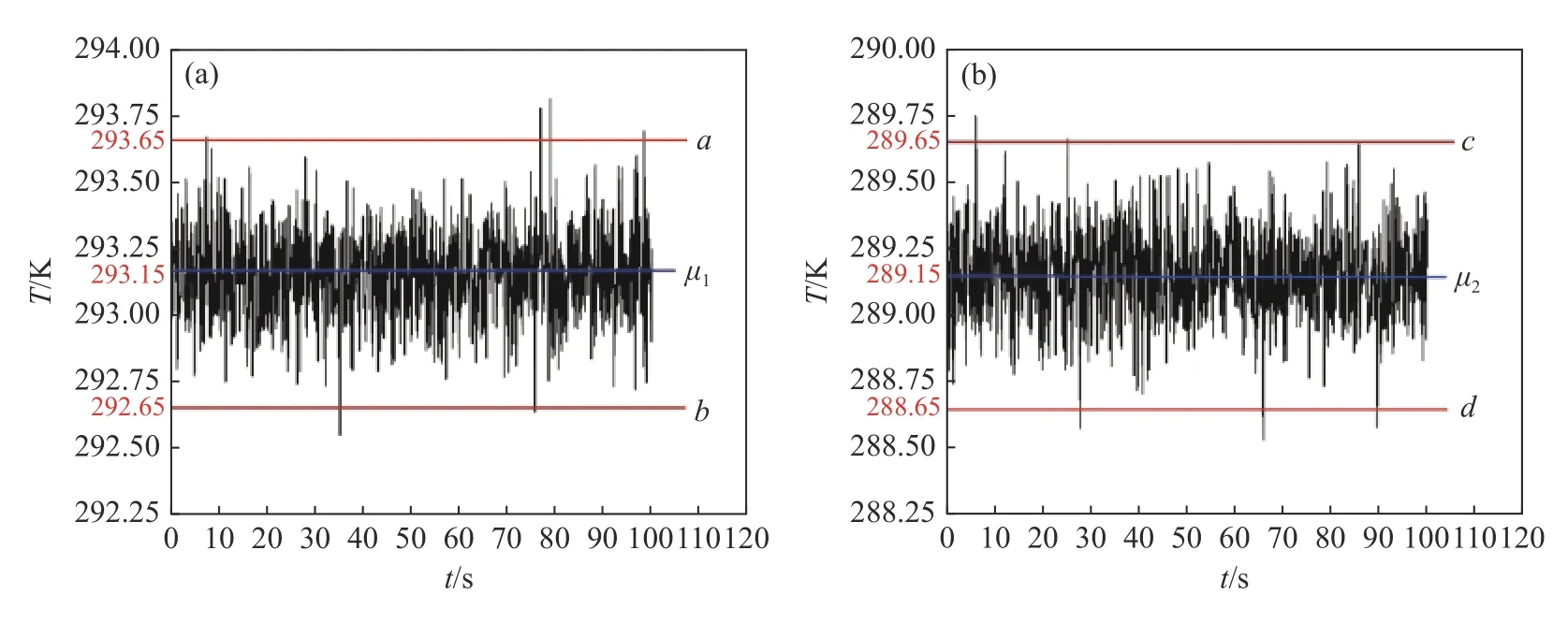
图6 实验室温度边界曲线。(a)高温工况;(b)低温工况Fig.6 Laboratory temperature boundary curve.(a) High temperature condition;(b) low temperature condition
在热仿真过程中,除了实验室环境温度边界输入条件不同外,其他初始设定条件均相同。一级热控结构实验室墙壁表面的热特性设置为ε1=0.8;二级热控结构抛光铝合金表面的热特性设置为ε2=0.1;二级热控结构内表面及真空舱外表面的热特性ε3=0.2;真空舱内部热沉的热特性为ε4=0.92。在一级热控结构与二级热控结构之间,以及二级热控结构与真空舱之间设置自然对流换热,对流换热系数为h=10 W/(m2·(°C))。同时,主动热控系统设置控温目标为293.15 K,PID 控制器控制参数Kp=50,TI=0.001,TD=150。若在上述两种工况下惯性传感器地面弱力测量系统的温度稳定性能满足相关要求,则表明在前述任意温度边界条件下该热控措施均能满足地面弱力测量热设计需求。
4.3 热分析结果
根据上述高温工况和低温工况的定义,在主动热控与被动措施两种条件下对两种工况进行了瞬态热分析和计算,并针对一级扭秤电极笼温度稳定性结果进行分析。高温工况和低温工况时,实验室流体环境与测量系统初始温度分别设定为293.15 K 和289.15 K。
图7(a)所示为高温工况下热分析计算中一级扭秤电极笼的温度变化曲线。由于三级被动热控结构具有良好的隔热效果,同时主动热控系统提供了温度补偿,一级扭秤电极笼在热仿真分析开始625 000 s 后逐渐趋于平衡。图7(b)所示为一级扭秤电极笼在瞬态分析平衡后24 h 内的温度曲线,从曲线中可以看出一级扭秤电极笼平均温度为293.147 447K,其最大温度变化值ΔTh=1.2×10-5K。同时对平衡后24 h 内的温度曲线进行了频域转换,具体如图8 所示,一级扭秤电极笼在24 h 内温度变化的均方根谱密度(振幅谱密度,ASD)表征了一级扭秤电极笼在频域内的温度稳定性。从曲线中可以看出,在0.1 mHz~1 Hz 的测量频带内,一级扭秤电极笼温度稳定性优于10-4K/Hz1/2。

图7 高温工况敏感结构温度变化曲线。(a)一级扭秤电极笼整体温度变化曲线;(b)一级扭秤电极笼24 h 温度变化曲线Fig.7 Temperature curves of the sensitive component under high temperature condition.(a) Overall temperature change curve and (b) the temperature change curve in 24 h of the electrode housing of primary torsion balance

图8 高温工况一级扭秤电极笼温度稳定性曲线Fig.8 Temperature stability curve of the electrode housing of primary torsion balance under high temperature condition
图9(a)所示为低温工况下热分析计算中一级扭秤电极笼的温度变化曲线。在主动热控制系统的加热补偿作用下,一级扭秤电极笼温度水平由低温工况初始温度值不断上升,并最终达到了平衡状态。图9(b)所示为一级扭秤电极笼在瞬态分析平衡后24 h 内的温度曲线,从图9(b)可以看出一级扭秤电极笼平均温度为292.943 001 K,其最大温度变化值ΔTc=1.6×10-5K。同时,对平衡后24 h 内的温度曲线进行频域转换。图10为一级扭秤电极笼在24 h 内温度变化的振幅谱密度。从图10 可以看出,在0.1 mHz~1 Hz 的测量频带内,一级扭秤电极笼温度稳定性优于10-4K/Hz1/2,满足热控指标需求。上述热分析结果表明,在不同的热分析工况下,热控制系统均能够保证惯性传感器地面弱力测量系统的敏感结构温度稳定性。
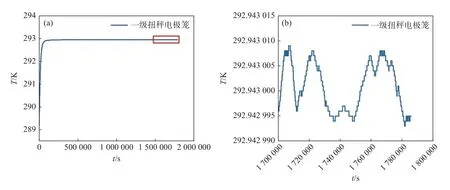
图9 低温工况敏感结构温度曲线。(a) 一级扭秤电极笼整体温度变化曲线;(b) 一级扭秤电极笼24 h 温度变化曲线Fig.9 Temperature curves of the sensitive component under low temperature condition.(a) Overall temperature change curve and (b) the temperature change curve in 24 h of the electrode housing of primary torsion balance
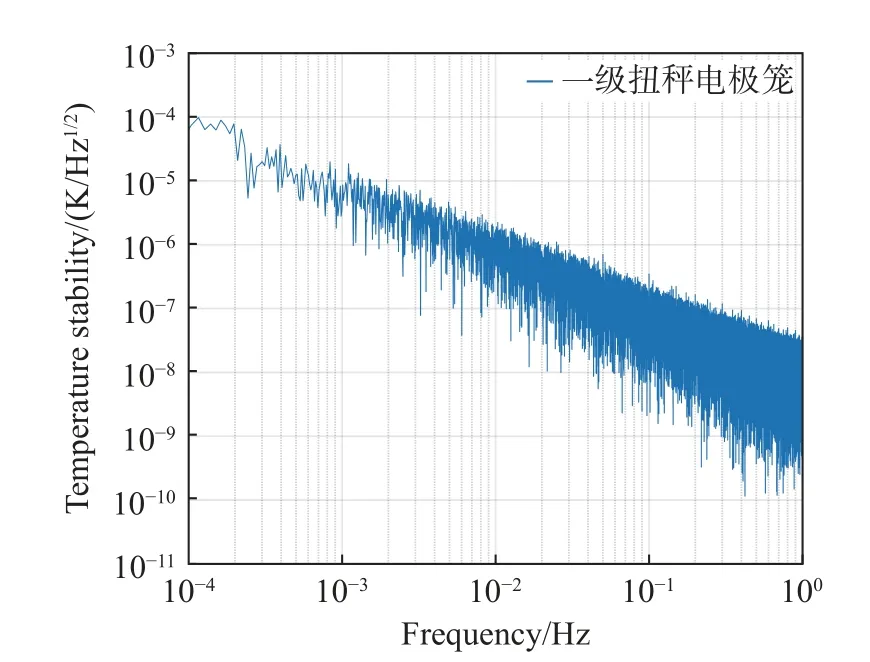
图10 低温工况一级扭秤电极笼温度稳定性曲线Fig.10 Temperature stability curve of the sensitive component under low temperature condition
在高温工况时无主动热控条件下热仿真计算中一级扭秤电极笼的温度变化曲线如图11(a)所示。在仅有被动措施的条件下,一级扭秤电极笼温度水平由初始值逐渐下降并最终达到了平衡状态。图11(b)所示为一级扭秤电极笼在瞬态分析平衡后24 h 内的温度曲线。从图中可以看出一级扭秤电极笼平均温度为293.099 884 K,其最大温度变化值ΔTc=4.33×10-4K。同时对平衡后24 h 内的温度曲线进行了频域转换,如图12 所示为一级扭秤电极笼在24 h 内温度变化的振幅谱密度。从图12 可以看出,在0.1 mHz~1 Hz 的测量频带内,一级扭秤电极笼温度稳定性优于5×10-3K/Hz1/2。对比上述热分析结果可以看出,在被动热控措施的基础上增加主动热控措施,可以更有效地抑制惯性传感器敏感结构的温度波动,使系统获得更高的温度稳定性。
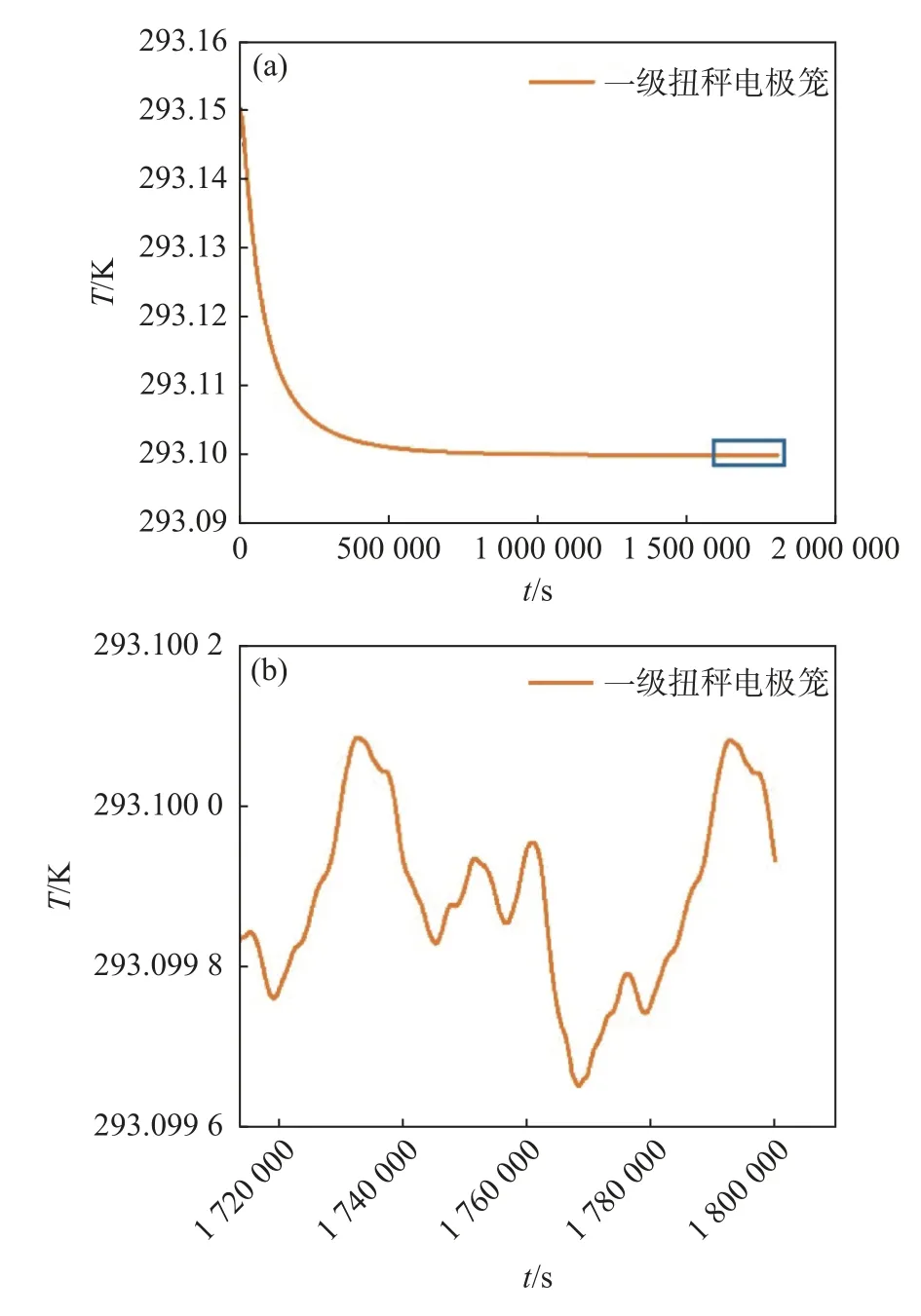
图11 高温工况无主动热控条件下敏感结构温度曲线。(a) 一级扭秤电极笼整体温度变化曲线;(b) 一级扭秤电极笼24 h 温度变化曲线Fig.11 Temperature curve of sensitive component under high temperature condition without active thermal control.(a) Overall temperature change curve and(b) temperature change curve in 24 h of the electrode housing of primary torsion balance
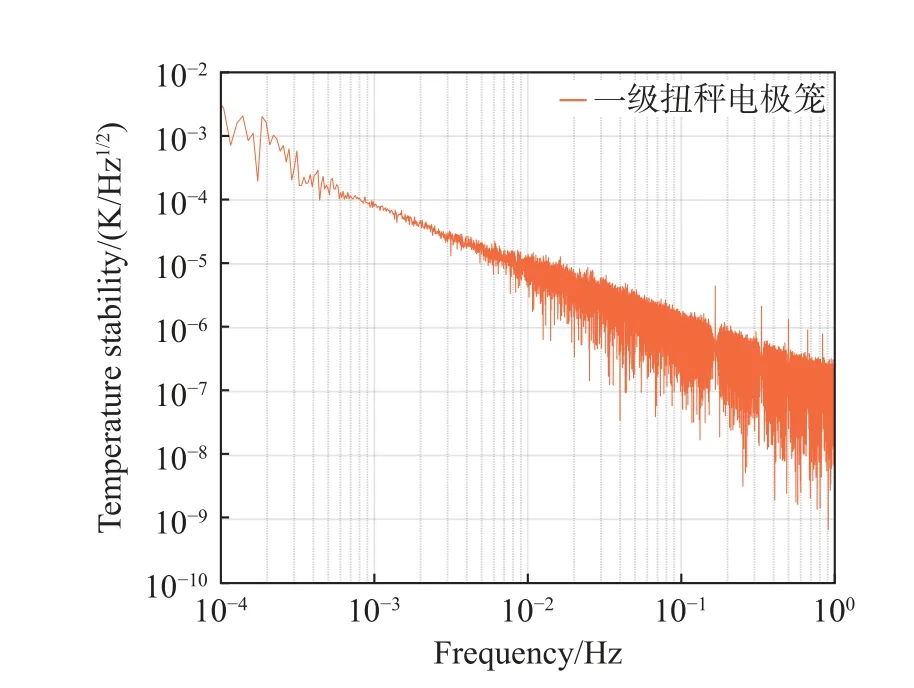
图12 高温工况无主动热控条件下一级扭秤电极笼温度稳定性曲线Fig.12 Temperature stability curve of the sensitive component under high temperature condition without active thermal control
5 结论
本文根据惯性传感器地面弱力测量系统的工作环境和温度稳定性需求,充分利用导热、隔热、散热等被动热控措施,辅以PID 算法控制的补偿电加热回路,设计了一套基于分级结构和PID 控制算法相结合的高精度热控制系统。考虑惯性传感器地面弱力测量系统所处的热环境,利用热仿真软件针对其高温工况和低温工况两种极端条件进行了瞬态分析计算,并将一级扭秤电极笼平衡后24 h 的温度曲线进行频域转换。分析结果表明,不同的工况下,在0.1 mHz~1 Hz 目标频段内,惯性传感器地面弱力测量系统敏感结构温度稳定性均优于10-4K/Hz1/2。结果表明该热控制系统能满足惯性传感器地面弱力测量系统的控温需求,验证了热设计的合理性。本研究为惯性传感器地面弱力测量试验的高精度、高稳定性热控需求提供了解决方案,同时对相关地面设备的精密热控研究也具有一定的参考价值。
猜你喜欢
杂志排行
中国光学的其它文章
- InGaAs/AlGaAs quantum well intermixing induced by Si impurities under multi-variable conditions
- Orbital-angular-momentum spectra in coherent optical vortex beam arrays with hybrid states of polarization
- The influence of the number of coupling regions on the output of the ding-shaped microring resonator
- A sliding-mode control of a Dual-PMSMs synchronization driving method
- Polarization-multiplexing of a laser based on a bulk Yb:CALGO crystal
- Compact voice coil deformable mirror with high wavefront fitting precision
