基于加窗法的孔道注浆缺陷定位检测技术改进分析

■翁 林

（福建省交设工程试验检测有限公司，福州 350000）

预应力混凝土桥梁结构在现代交通工程中广泛应用，一般分为体内预应力和体外预应力两种结构体系， 其中体内预应力结构体系应用更为广泛。体内预应力钢绞线张拉完毕后，需要在预应力孔道内注浆，排净孔道内的水和空气，预防预应力钢绞线腐蚀；同时注浆后的预应力孔道与周围混凝土形成一个整体，应力分布更均匀，避免钢绞线发生松弛现象。 为此，孔道注浆质量尤为重要，必须保证浆料“充盈”“饱满”和“密实”[1]。 为了确保预应力孔道注浆质量，必须对孔道注浆密实度及缺陷定位进行检测。 常用的孔道注浆密实度及缺陷定位检测方法有冲击回波法、超声波法和探地雷达法[3]。 其中，冲击回波法在可行性和检测效果方面应用最为广泛。然而，冲击回波法仍然存在一些问题，如频谱信号稳定性受梁体结构及其他外界因素的影响较大，信号特征有时不明显等[4]。 为了优化冲击回波法在孔道注浆密实度检测中的应用，本文将对冲击回波法在孔道注浆密实度检测中存在的问题进行详细分析研究，并提取相应的改进方法进行优化，以提高检测效果和准确性。

1 冲击回波法技术概述

冲击回波法是一种常用的孔道注浆缺陷定位检测方法。 它通过在预应力孔道中施加冲击并监测由此产生的回波信号，以此来确定孔道中的缺陷位置和大小[1]。

1.1 冲击回波法检测原理

冲击回波法在预应力孔道注浆缺陷定位检测中被广泛应用的原因如下：（1）检测精度高，检测精度能到厘米；（2）受钢筋影响小，弹性波信号对钢筋钝感；（3）对混凝土中缺陷敏感，混凝土材质同不良区域材质波阻抗差异大[4]。

冲击回波法原理如图1 所示，通过在被测结构表面敲击产生瞬态的弹性波，弹性波会在结构体内传播，当遇见波阻抗变化的材质（缺陷、底面）时，弹性波会被反射，当反射波到达测试面后，又会再次反射在构件中进行传播，形成冲击回波，该回波信号会被加速度传感器所接收。 传感器接收波形图如图2 所示。 通过对波形图进行频谱分析，提取其信号卓越频率f， 结合波速v 即可对混凝土结构或缺陷深度h 进行计算。 计算公式见式（1）。

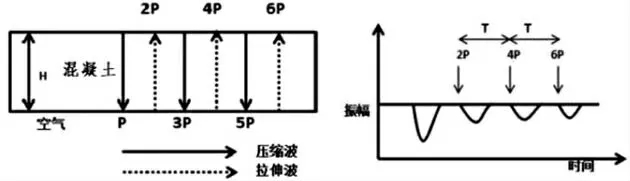
图1 冲击回波法原理

图2 传感器接收波形图

冲击回波法可以判断的孔道注浆的缺陷类型有压浆密实、压浆有缺陷、未压浆等，具体如图3 所示。

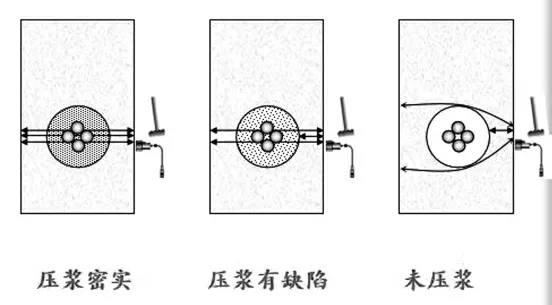
图3 孔道注浆缺陷检测类型

1.2 冲击回波法适用性分析

冲击回波法主要分析的信号成分为纵波，纵波在半无限大介质中以球面波形式扩散，能量衰减较大，因此冲击回波法更适用于板式混凝土结构，并且在孔道注浆密实度的检测中只能对单排孔道进行检测[5]。

冲击回波法的缺陷识别分辨率取决于缺陷的径深比（≥0.3），而且通常适用于板厚在80 cm 以内的单排孔道注浆检测[5]。 因此，实际检测中，需要考虑被测结构的特点和要求，并综合使用其他适用的方法来提高检测的准确性。

1.3 频谱泄漏问题分析

冲击回波法在数据处理中将信号视为周期性的回波信号，但实际上信号的开始同信号结尾存在不连续性。 当使用FFT（快速傅里叶变换）进行频谱分析时，其假设信号是周期性的，同实际冲击回波信号的不连续性特征相悖，因此会导致额外的频率出现，这被称为泄露现象[6]。 这种泄露会对真实频率造成干扰，从而影响信号的频谱分析结果。 这一现象可以在同一测点上不同采样时窗的信号对比中得到印证。采样时窗更长的信号尾部更为平滑（图4（b）），同起始信号大小更为趋近，对2 种采样时窗信号进行频谱分析，结果如图5 所示。图5（b）中，频谱更为集中，主频信号更突出。 虽仍存在频谱干扰信号，但不难看出信号首尾的衔接程度会对频谱集中性造成直接的影响。 为了更好地解决频谱泄露问题，本研究采用加窗法对冲击回波信号进行改进。

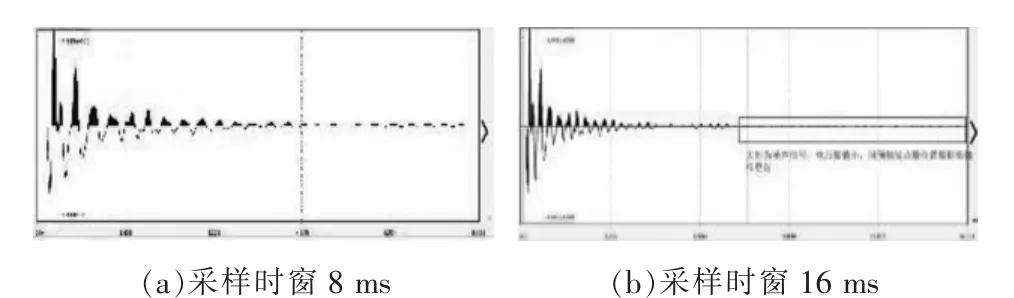
图4 冲击回波信号分析

图5 冲击回波频谱分析

2 基于加窗法的冲击回波法信号改进技术

信号窗函数是一种在信号处理中常用的函数，用于截断或加权原始信号，窗函数在特定的时间窗口内非零，窗口外则为零，通过将其同原始信号进行逐点相乘来实现截断及加权操作，从而改变信号特性，减小信号的边缘效应和泄露现象。窗函数在频谱分析中通常与傅里叶变换一起使用。因此，本项目引入加窗法对冲击回波法的数据进行处理分析。

2.1 加窗函数对比试验

常见的信号窗函数包括汉宁、汉明、矩形窗等。每种窗函数都有其独特的数学形式和特性，选择合适的窗函数取决于信号处理目标及对频率分辨率和频谱泄漏的要求。 结合冲击回波法的技术特性，采用不同类型窗对冲击回波法数据进行处理，对比其效果。 3 种常用的窗函数图如图6 所示。

图6 3 种常用的窗函数图

汉明窗函数式[6]如下：

式 （2） 中：n 为当前数据点位置；N 为采样点数；a0为经验参数值（汉明窗函数取值0.538）。 当a0=0.5 时，该函数为汉宁窗函数。 矩形窗函数[6]公式如式（3）所示：

分别采用3 种窗函数对实测冲击回波数据进行加窗处理，FFT 分析得到其频谱图，如图7 所示。由图7 可知，汉明窗频谱图主频信号最为集中、稳定，因此本文采用汉明窗对冲击回波法数据进行加窗处理。

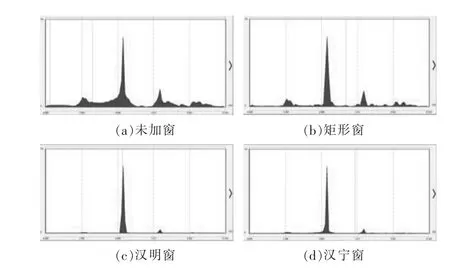
图7 各类窗函数频谱图

2.2 加窗范围的确定

应用窗函数时，要考虑窗口长度，正确设置加窗范围可以提高信号处理的效果和准确性。 采用冲击回波法检测孔道注浆密实度时，通常采样时窗为8.192 ms，为了对信号加窗范围进行确定，采用小波时频法对冲击回波信号进行分析（图8），以确认有效信号范围。

图8 冲击回波信号小波时频图

从时频图（图8）中可知，冲击回波信号的有效范围约为0.5～5 ms 区间。 对加窗范围0～8.192 ms及加窗范围0.5～5 ms 的2 种参数采用同一组数据进行分析对比，可得到图9。可知，加窗范围0.5～5 ms 时明显效果更佳。

图9 加窗范围对比数列频谱图

综上所述，冲击回波法中加窗函数类型确定为汉明窗，加窗范围宜为0.5～5 ms。

2.3 标准试块数据加窗试验

采用冲击回波法对砼标准试块（15 cm×15 cm×15 cm）进行测试，对测试数据进行加窗前后频谱分析对比。 标准试块如图10 所示，试块数据加窗前后频谱对比如图11 所示。

图10 混凝土试块（C30）

图11 试块数据加窗前后频谱对比

由图11 可知，加窗后，试块底部反射位置对应的频谱更加尖锐，频谱泄露状况能得到明显提升。

3 模型试验和现场验证

为验证加窗法在孔道注浆缺陷定位检测中的应用效果，分别在模型及现场进行了试验验证。

3.1 模型试验

模型梁腹板厚0.7 m，长8 m，采用D30 锤，采样时窗8.192 ms，前期标定得到混凝土波速为4.1 km/s。图12 为测试数据未加窗分析的频谱图， 可见底部反射信号附近的干扰信号较多。 对该数据进行汉明窗加窗处理，得到结果如图13 所示。 结构底部反射信号连续性、稳定性得到显著增强。

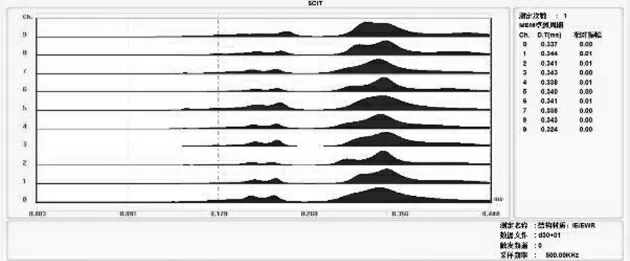
图12 未加窗信号频谱图

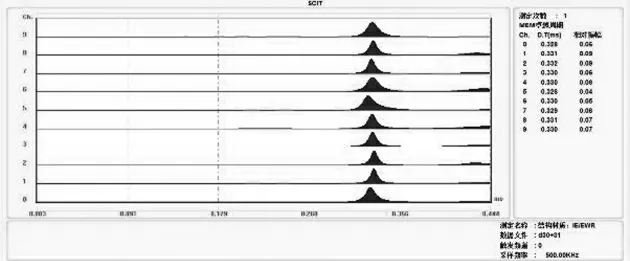
图13 加窗后信号频谱图

3.2 现场验证

3.2.1 小箱梁现场测试

某梁场内预制箱梁长20 m，梁底宽1 m，梁高1.3 m，混凝土设计强度C50，注浆龄期为45 d，满足检测要求。预制箱梁现场如图14 所示。采用冲击回波法对其孔道注浆密实度进行检测。 该梁腹板厚度为20～28 cm 渐变，测点间距为10 cm，对测试数据进行频谱分析对比。 未加窗及加窗后频谱图分别如图15 所示。

图14 某梁场预制箱梁

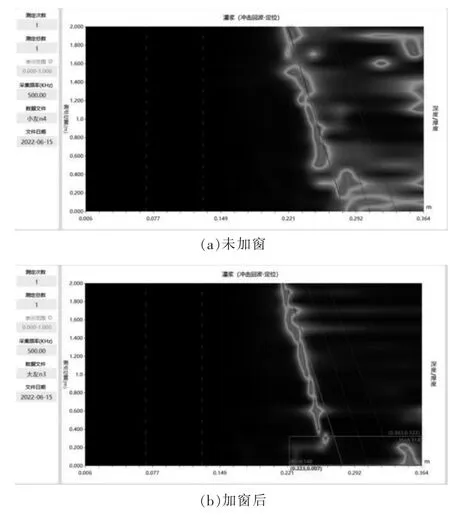
图15 N1 孔道频谱等值线图

结果显示，加窗前，信号频谱图中存在较多干扰信号，同时测线0～0.4 m 位置的缺陷信号特征不明显；加窗后，信号明显更为集中、干净，0～0.4 m 缺陷的信号延后特征变得更为明显。 后经开孔验证，该孔道距端头位置0.4 m 内存在注浆缺陷， 验证情况同检测结果一致。

3.2.2 T 型梁现场测试

某梁场内预制T 梁全长约30 m， 梁高1.8 m，腹板厚度30～40 cm 渐变，混凝土设计强度C50，注浆龄期为42 d，满足检测要求。 预制T 梁现场如图16 所示。 采用冲击回波法对该预制T 梁孔道注浆密实度进行检测。 该梁腹板厚度为30～40 cm 渐变，测点间距为10 cm，对测试数据进行频谱分析对比。 未加窗结果及加窗后频谱图分别如图17 所示。

图16 预制T 梁

图17 N3 孔道频谱等值线图

由图17 可知，未加窗时，频谱信号集中度、连续性差，显示为大面积的信号滞后，同实际验证情况存在偏差。 加窗后，频谱信号更为集中连续，显示为端头0～1.3 m 信号滞后，同实际验证情况相符。

4 结语

经模型试验分析及现场验证，表明冲击回波法能够有效地对预应力孔道注浆缺陷进行定位检测，同时基于加窗法的改进算法能有效提升冲击回波法的检测效果，能够让信号频谱图更为集中、稳定性更强的同时增强缺陷信号特征从而减少误判。 本文创新性地提出在孔道注浆密实度缺陷定位检测（冲击回波法）信号分析中引入加窗法，有明显的效果及应用前景，能为实际工程应用中的数据分析提供新思路。