基于DEA 模型的高速公路工程项目效益评价

■苏 华

（福建省交通规划设计院有限公司，福州 350004）

1 绪论

近年来，我国新建设高速公路里程规模逐年递增[1]，工程前期如何对高速公路项目进行效益比较，通车运行后对项目投入产出如何进行分析，分析项目的全过程效益，成为行业可持续发展亟待解决的问题。 目前，高速公路项目的效益评价主要依赖于专业机构编制的分析报告， 包括可行性分析和后评价分析等[2]，涉及自然地理条件、产业规划、交通运输现状和城市建设等复杂问题[3-4]。 尽管交通运输部已提出了相关评价规范[5]，许多学者也从不同角度，例如车辆运营成本[6]、新技术[7]、财务分析[8]、综合分析[9-12]等方面提出了改进，但仍然缺乏客观系统地将各种综合指标进行分析判定，构建完善评价模型的效益评价研究。 而数据包络分析（Data Envelopment Analysis，DEA）[13]方法则具有自我赋权，可计算目标差距与目标效率，以及量纲统一等优点，已经用于产业优化[14]、农田水利工程[15]、企业发展策略研究[16]等方面，具有良好的适用性，并在效益分析上表现良好。 通过梳理国内外研究现状，基于已发现的问题，本研究拟采用DEA 方法分析高速公路项目效益，以熵权法及层次聚类法构建项目方案的分类评价模型，并以福建省15 例高速公路工程实例进行运算和验证。

2 方法

2.1 数据包络分析法（DEA）

数据包络分析法（DEA）是用于评价具有多个投入、产出指标的决策单元（DMU）之间相对效率的一种非参数评价方法。 根据研究对象的不同，其模型具有多种形式，包括CCR 模型、BCC 模型、Super-SBM 模型等[17]。 由于高速公路项目投入产出的边际价值相对规模变化较低，且效率值差异较小，Super-SBM 模型较为适用[18]。 该模型的优势在于直接将松弛变量加入函数中，从而在其他模型仅能比较方案是否有效的情况下，该模型可比较不同方案的效率值大小， 并可考虑松弛输入和松弛产出的影响，不受规模报酬变化的影响[19]。 因此，采用Super-SBM模型适用于高速公路项目可行性的评价，以下将对该模型的算法展开说明。

假设将要评价的决策单元有n 个，每个决策单元有m 种输入以及s 种输出， 投入和产出变量分别用x和y 表示，则Super-SBM 模型可表示为：

式中，δ*为综合技术效率值，xi0和yr0分别表示被评价单元的投入量和产出量，λ 是权重向量，当δ*＜1 时， 该决策单元综合技术效率较低； 当δ*≥1时，该决策单元综合技术效率较高；δ*越大，则决策单元的综合技术效率越高。

2.2 确定输入输出指标体系

对于一个DEA 评价系统而言， 理想状态是以最小的投入获得最大的产出，而对于高速公路工程项目而言，则是期望以最少的路线长度、工程规模、征地拆迁数量、工程造价等，获得最大的经济效益、社会效益、环境效益[20-22]，其中，经济效益以累计经济效益（累计国民经济净现值，ENPV）进行评价，计算公式如式（3），社会效益以提供就业岗位数量评价，按照对应工可报告因地制宜进行研究，每亿元投资创造岗位约1500～2000 个[23]，环境效益以累计节省能耗评价，依照式（4）～（6）进行计算，通过比较各方案的对应输出指标，计算效率值，即可比较各项目中的最大效率， 并得到各方案的松弛变量，从而对各方案的效益进行评价。 所有指标的计算期限均按《公路建设项目经济评价参数与方法》规定的20 年运营期进行计算。

（1）累计国民经济净现值计算

式中：Bt为第t 年国民经济效益流入量（元/年）；Ct为第t 年国民经济费用流出量 （元/年）；Bt-Ct为第t 年国民经济净效益流量（元/年）；t 为国民经济评价计算期（年）；Is为社会折现率（%），本研究中设定为8%。

（2）累计节省能耗计算

累计节省能耗以燃油节约量F 进行计算，并在计算完成后，换算为万t 标准煤。

式中：F1为拟建项目燃油节约量（L）；F2为原有相关公路燃油节约量（L）。

式中：T1p为有项目情况下拟建公路的趋势型交通量（辆/日）；T2p为有项目情况下拟建公路的诱增型交通量（辆/日）；FOC′1b为无项目情况下，原有相关公路趋势型交通量条件下的各种车辆的平均油耗（L/百车公里）；FOC2p为有项目情况下，拟建项目在诱增型交通量条件下的各种车辆的平均油耗（L/百车公里）；L 为拟建项目的路段长度（km）；L′为原有相关公路的路段长度（km）。

式中：T′1p为有项目情况原有相关公路的趋势型交通量（辆/日）；T′2p为有项目情况原有相关公路的诱增型交通量 （辆/日）；FOC′2p为有项目情况下，原有相关公路在诱增型交通量条件下的各种车辆的平均油耗（L/百车公里）。

2.3 熵权法计算整体可优化值

为考察项目方案整体上的可优化性，使用熵权法对DEA 计算得到的松弛变量进行赋权， 获得整体可优化值。 整体可优化值表征的是单一方案可优化的潜力大小，当整体可优化值越大时，证明此方案可优化的空间越大。 在综合技术效率相同时，整体可优化值越大，说明此方案在维持不低于原来效率的情况下，可以减少投入资源，获得更多的产出。

熵权法是一类不依赖于主观评价的客观赋权方法，它以数据的变异程度计算各类数据的权重[24]，具体过程如下。

（1）原始数据收集与整理。 本研究共需要评价15 种项目方案的9 种松弛指标，初始数据矩阵如下：

其中m=15，n=9，xij表示第i 个评价方案第j 项松弛变量的数值。

（2）指标归一化处理。 指标归一化与标准化的目的相同，即消除不同指标不同量纲的差异。 将指标归一化到[0，1]，归一化 后的矩阵为bmn，bij表示第i个项目方案第j 项松弛变量的归一化数值。

（3）计算熵值。 熵值计算公式为

（5）计算各个方案的整体可优化值。 计算公式如下：

式中，Optj 为第j 个方案的整体可优化值。

2.4 层次聚类法

经过熵权法得到整体可优化值后，采用层次聚类法进行分类。 层次聚类算法不需要预先指定聚类个数，可以自动得到聚类层次结构[25]，本研究采用凝聚类型聚类中的类平均法（Average Linkage）进行层次聚类。

3 分类模型建立

3.1 数据导入

采用多条福建丘陵地区高速作为模型计算实例，基于前文构建的输入输出指标体系，通过DEASolver 软件计算Super-SBM 模型，将指标体系和输入输出数据代入输入软件，从而求得各个方案的效率值并分析，导入数据见表1。

表1 综合评价模型导入基础数据

根据指标体系和输入输出数据， 代入Super-SBM 模型利用线性规划模型和公式可以计算出各决策单元的效率值，计算结果见图1 和表2。

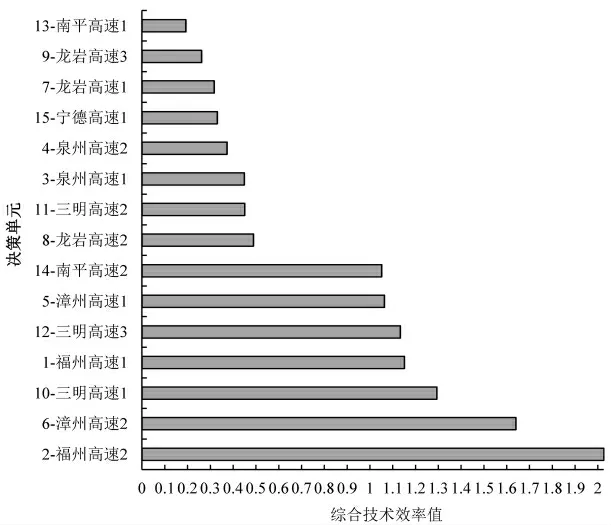
图1 DEA-Solver 计算结果排序

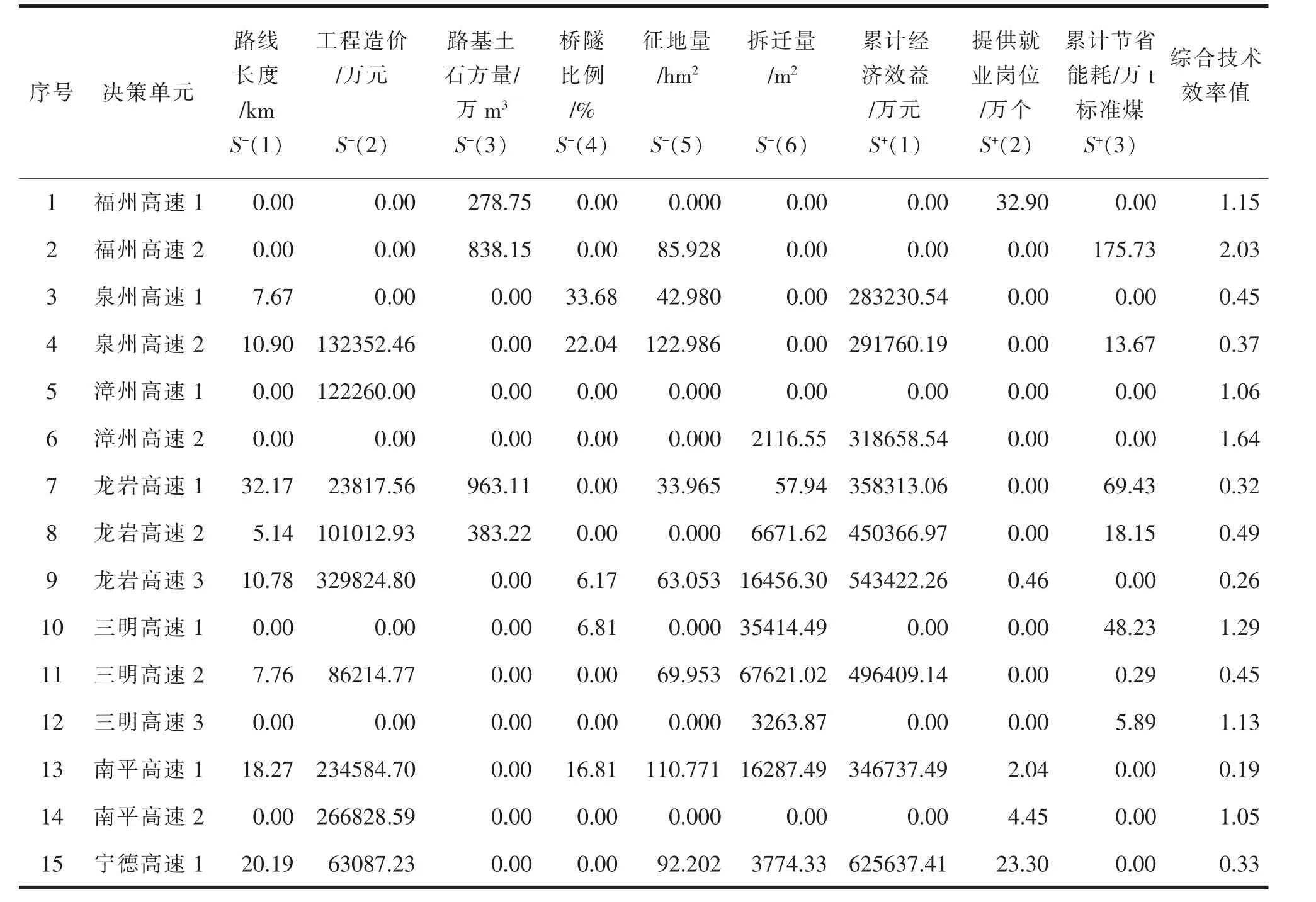
表2 模型松弛变量分析

3.2 综合技术效率分析

DEA-Slover 计算得出的各决策单元综合技术效率值表明，共有7 个项目方案综合技术效率较高，占所有项目方案的50%；而另外7 个方案的综合技术效率值低于1，说明这7 个项目相较于其他比较的项目投入产出效率比较低。 而在其他效率较高的项目方案中可以看出，福州高速2 方案的综合技术效率值最高，为2.03，说明在比较的14 个项目方案中，福州高速2 方案的效益对资源的利用程度最高，可行性也最好，其次是漳州高速2 方案，与福州高速2 方案相差0.39 的效率值，而南平高速2 方案的综合技术效率值在8 个效率较高的方案中最低，为1.05，投入资源得到的结果最差。图1 中的综合技术效率值结果仅反映了15 个项目方案的相对效率水平，并没有说明造成各个方案相对效率不高的原因及程度。 因此，需对各个项目方案进行松弛变量分析，通过分析计算在每个指标影响下项目方案与最优决策单元之间的距离大小， 进而明确非DEA 效率较高的原因和差距水平。

3.3 松弛变量分析

表2 中，输入指标松弛变量的变化值为负值（S-），输出指标变化值为正值（S+）。在松弛变量的分析中，当决策单元接近于生产前沿面，其投入产出指标的松弛变量越接近于0，而其他决策单元的松弛变量存在变化，表明其他决策单元可以通过调整资源的投入获得不同产出，且调整的方向和幅度有所不同。若某一指标相对其他指标来说，需要改变的幅度在原始值中所占的比例较大，则说明该指标是导致综合技术效率值降低的重要因素。 在7 个技术效率较低的方案中，南平高速1 的主要问题是投入资金、征地量和拆迁量过剩，桥隧比例过大，但其所获得的经济效益则较少；龙岩高速3 方案主要的问题是土石方量和拆迁量过多，而输出指标低。 而在8 个技术效率较高的项目方案中，综合技术效率最高的方案为福州高速2 方案，但在维持相同造价和拆迁量时，可考虑增加环境效益，例如项目路线选择要遵循“近城不进城”的原则，沿线走廊带要充分考虑使附近城镇、厂矿等车辆上下高速公路方便快捷，从而提高路线所节约的燃油量，以及积极推广废旧沥青混合料再生利用、改性沥青、乳化沥青等环保经济型技术在养护工程中的运用；其次是三明高速1方案综合利用效率较高，并且方案调整空间较小，但在拆迁量和经济效益上仍有改善的空间。 同时，在多数综合技术效率较高的方案（综合技术效率值大于1.06）中，相较其他效率低的方案，其共同特点是在改进方案时，无需调整工程造价，表明技术效率较高方案的共同特点之一是资金利用合理。 此外，这些方案的土石方量和拆迁量较其他方案低，表明其在工程可行性研究的合理性方面的相对优势。 值得注意的是，在最优方案福州高速2 方案中，土石方量和征地量上有着相当大的优化空间，可能与高速公路部分路段地势平缓且靠近城镇有关联。

3.4 松弛变量赋权

基于前文的计算步骤，以熵权法对归一化后各松弛变量计算权重，结果如表3 所示。

表3 归一化后熵权法计算结果

3.5 层次聚类

基于上文计算步骤， 根据过往研究和经验通则，本研究设定分类簇为3 种，得出层次聚类结果如表4、图2 所示。

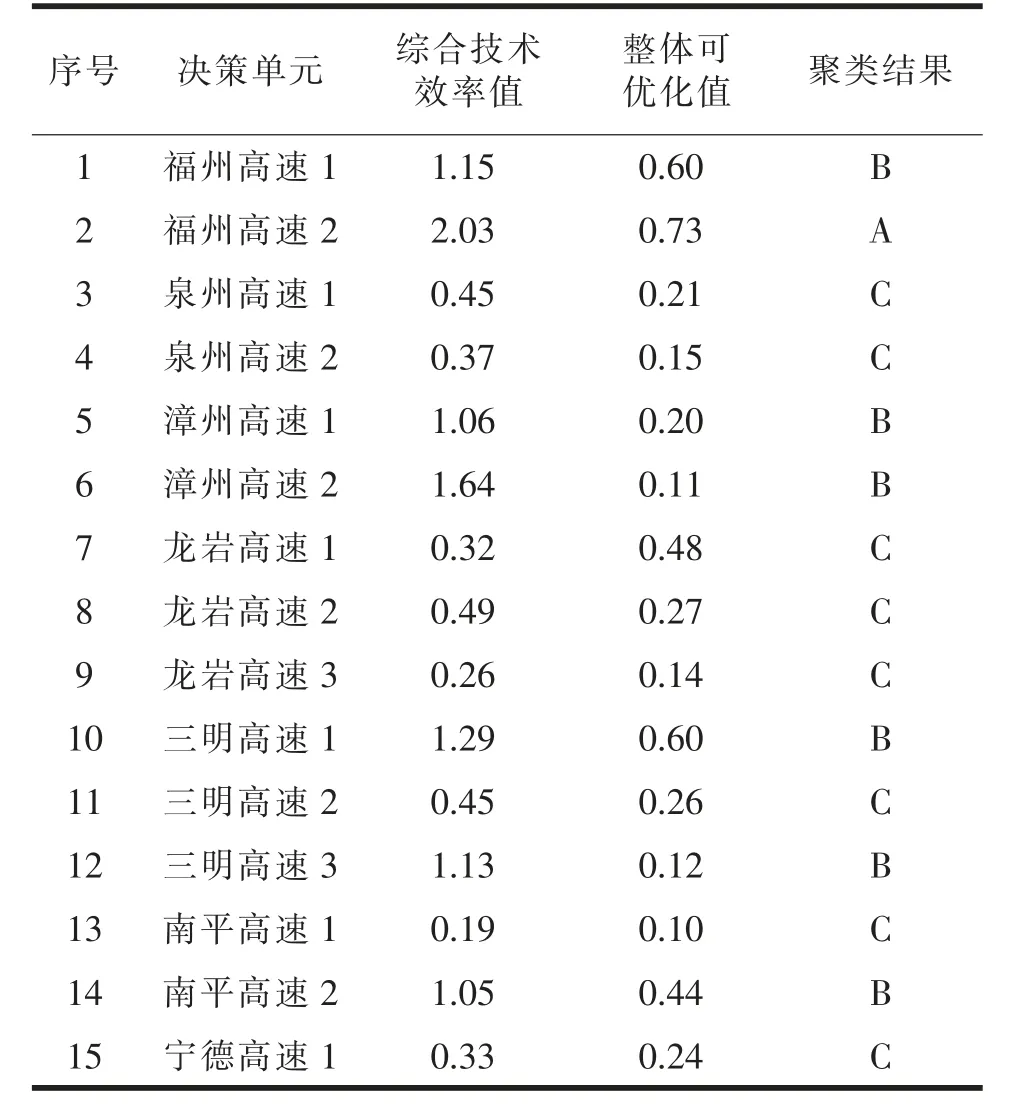
表4 层次聚类结果

15 个项目方案中共有1 个方案被分类为A类，6 个方案被分类为B 类，8 个方案被分类为C 类。其中，福州高速2 方案被视为最优的A 类项目，而综合效率值低于1 的8 个项目方案被分类为C 类，与上文的分析较为吻合。

4 结论与展望

本研究基于Super-SBM 模型， 以路线长度、工程造价、路基土石方量、桥隧比例、拆迁量、征地量为输入指标，以累计经济效益、提供就业岗位数量、累计节省能耗为输出指标， 计算了其综合效率值，分析了各方案的松弛变量，并以熵权法计算松弛变量的整体可优化值，基于综合效率值和整体可优化值， 以层次聚类方法构建了高速公路项目方案的A、B、C 效益评价模型， 以近年以福建省15 个高速公路不同建设方案为模型计算实例，得出主要结论如下：（1）本研究输入输出指标选取合理，均具有代表性，尤其是输入指标中土石方量、拆迁量影响项目效益优劣的程度较明显，说明在实际工程可行性研究中，土石方量和拆迁量的减少相对于其他层面更有利于提升项目的综合效益，为今后研究提升山区高速公路方案中的综合效益提供了倾向性的设计方向。 （2）本研究构建的综合效益评价模型客观地评价了不同建设方案间综合效率的优劣，有利于当前单一项目工程可行性评价的效率优劣评判从缺乏横向对比、评判具有局限性走向客观性、综合性的对比；通过后续项目数据的补充建立动态评价库，有利于建立更加客观、系统、科学的评价模型。（3）通过熵权法赋权及层次聚类，在15 个项目方案中，共有1 个方案被分类为A 类，6 个方案被分类为B 类，8 个方案被分类为C 类。 其中，福州高速2方案被视为最优的A 类项目。这一结果可应用于工程项目的评价分类中，未来可以此标准进一步收集数据，建立基于大数据的项目评价数据库，为高速项目全过程中的评价分类提供帮助。 （4）本研究构建的分类模型展现出较好的区分度，并可为方案选择、优化改进提供思路。 但由于未考虑到更加具体的因素，如项目行车安全指标、施工工期等因素，模型可能存在一定的误差，未来可在此基础上开展进一步的研究，以获得更加精确的结果。 （5）本研究选取的案例仅为南方山区，未来可针对不同地区，如平原、高原、沙漠等不同区域的高速公路，建立项目评价数据库，并从项目效益评价方面对C 类项目提出改进思路，同时可补充更多可量化的输出指标，为类似项目的评价及优化提供帮助。