弹性支承转子系统应变能分析及其支承特性影响研究*

王美令 胡秋生

（大连交通大学机车车辆工程学院）

0 引言

以航空发动机为代表的高速旋转机械转子系统普遍采用弹性支承，用以调整和控制系统的临界转速，以保证系统在工作转速范围内通过低阶临界转速时，大部分变形集中于弹性支承上，从而保证系统稳定运行。然而，随着转速不断增大，支点数目的减小，转子相对于支承的刚性弱化，在高转速工作时易出现弯曲变形[1]，同时，当支承刚度高于某一定值时，会使转子刚体振型弯曲应变能过大，呈现弯曲较大的振型，对振动不利。转子应变能是指转子发生形变时，外力在形变位移上所做的功，其分布可用于表征转子变形和受力状态[2]。综合考虑转子刚度和支承刚度的影响，掌握其相对刚度特性对系统应变能分布的影响规律，对于转子系统的分析设计具有重要的指导意义。

支承特性对转子系统动力学特性乃至整机振动具有重要影响。众多学者针对转子系统支承特性及其对系统影响开展了大量的研究工作。罗忠等[3]建立了带弹性环式支承结构的转子系统有限元模型，研究了转子系统在静刚度和动刚度条件下对临界转速的影响。乔留春[4]基于有限元和试验方法，提出了弹性支承结构的动刚度辨识方法，并开展了相关参数对弹支支点刚度的影响分析。邓旺群等基于试验研究分析了带柔性过渡段悬臂动力涡轮转子系统的动力学特性，获得支承刚度对其影响，并提出支承刚度的修正方法。并基于不同的支承刚度和轴向位置，开展了某型发动机低压转子的临界转速随支承刚度和轴向位置变化规律的研究[5-6]。屈美娇等[7]通过定义转静耦合因子和截面转静碰摩危险系数，定量研究了支承刚度对试验器固有频率、整机模态振型、转子静子耦合程度、压气机和涡轮截面转静碰摩危险程度的影响。Yan等[8]对比研究了前、后两端分别为柔性支承和刚性支承的转子-轴承系统的振动特性。Harsha 等[9]研究了带滚动轴承支承对于刚性转子系统动态响应的影响规律。王龙凯等[10]基于航空发动机等复杂转子-支承系统的通用动力学模型，从转子固有特性、应变能分布、支承传递力和振动响应等方面对弹性支承并联SFD非线性减振效率进行分析。太兴宇等[11]将弹性基础的特性引入到转子系统中，分析了弹性基础对转子系统横向振动的影响规律。赵芳慧等[12]建立多平行轴系-轴承-箱体混合模型并开展其动力学特性研究，分析了柔性支撑对轴系固有模态特性的影响规律。

本文为了研究弹性支承特性对转子系统应变能分布等动力学特性影响，以两支点支承的转子系统为研究对象，建立其动力学模型，在此基础上给出了应变能的计算公式，分析了支点支承刚度、刚度不对称对转子系统的模态振型及相应的应变能分布的影响规律。

1 基于有限元法的转子系统模型及其模态应变能分析

1.1 基于有限元方法的转子系统动力学模型

针对由轮盘、转轴、弹性支承结构和支座等部件组成的转子系统是典型的两支点转子系统，采用有限元方法进行建模和理论分析，并采取如下的简化处理：1）转轴视为具有均布质量的弹性轴；2）轮盘视为具有回转效应的刚体，简化为集中质量和转动惯量；3）基座、支座设为刚性；4）将弹性支承结构视为线性，简化为线性弹簧-阻尼单元，作用在转子支点处。

基于有限元方法离散转子系统的过程中，对单元节点进行连续编号。假设转子系统共有m个节点，则整个转子系统共有n=6m个自由度，系统的质量矩阵、陀螺力矩矩阵、刚度矩阵均为n×n阶。转子系统整体节点位移矢量为

在得到了转子系统的整体质量矩阵、刚度矩阵和陀螺力矩矩阵后，即可获得转子系统的动力学方程

引入比例阻尼后，系统的动力学方程可记为

式中，q，，分别为系统所有节点的振动位移、速度和加速度列阵；M为系统质量矩阵；G，K分别为系统的陀螺力矩矩阵和刚度矩阵；Q为系统的广义激振力矢量，包含不平衡激励力和可能存在故障激励力。引入的阻尼矩阵C记为

1.2 转子系统应变能分析

对于自由振动状态，转子系统不受力作用，转子系统的运动方程(3)可以改写成

为了求解这个方程的特征值，把原始系统的n×n阶方程扩展到2n×2n阶，得到

对于自由振动，位移有以下形式U

式中，Φ表示位移U的振幅；ωˉ和t分别表示特征值和时间。

将式(8)代入式(6)，得

这个方程是标准特征值的问题。通过上述分析，得到系统的振型，包括各节点的广义位移（位移、转角），在此基础上进行系统的应变能分析。转子系统的总应变能包括：转子的弹性应变能（弯曲应变能、剪切应变能）、弹支支承的应变能。系统总的应变能Us可表示为

式中，q为系统的广义位移向量；K为系统的刚度矩阵。

弹性支承的总应变能Ue可表示为

式中，Uei为第i个弹性支承的应变能(i=1:m)；qi为弹性支点处的广义位移向量；Kei为第i个弹性支承的刚度矩阵[13]。

由于振型的变化与转子、支承的变形能分布有关，通过转子支承系统的应变能在转子、支承系统的分布（即所占的比例）可有效地确定转子系统的模态振型。

定义转子的应变能系数η，即转子的弹性变形能在系统总应变能中所占的比例，可表示为

式中，Us为系统总的应变能之和；Ue为系统支承的弹性应变能。

在以航空发动机为代表的高速旋转机械结构设计中，希望在工作转速范围内的临界转速下转子应变能不超过发动机总应变能的20%～25%，以限制转子在临界转速时不能有太大的弯曲，尽可能接近刚体振型[14]。在本文系统模态振型分析中，采用引入的转子应变能系数来区分、评定模态振型。

2 支承特性对系统模态特性的影响

2.1 算例

针对典型两支点弹支-刚性转子系统，建立其有限元模型(如图1所示)，通过数值仿真分析支承刚度、支点刚度不对称对转子系统的模态振型及模态应变能分布的影响规律。弹支转子系统的支承刚度是由轴承刚度和弹性鼠笼结构刚度串联得到的，而弹支鼠笼结构远小于轴承刚度(量级1e6N/m)，因此，支承刚度主要由弹支鼠笼结构的刚度决定。分析中系统的基本参数如表1所示。

图1 两支点转子系统有限元模型Fig.1 Finite element model of two-fulcrum rotor system

表1 转子系统的基本参数Tab.1 Basic parameters of rotor system

采用上述的转子系统有限元建模方法，建立的转子系统的有限元模型(如图1所示)，系统共有11个节点，每个节点6个自由度，共66个自由度，转盘位于6#节点处，系统两端的两支点分别位于2#、10#节点处，转轴分为10段，轴段参数如表2 所示。转子系统的广义坐标为1×66 维的位移矢量，可记为

表2 转子系统的轴段单元参数Tab.2 Shaft segment element parameters of rotor system

组集得到的系统质量矩阵M为66×66 阶稀疏对称矩阵，陀螺力矩矩阵G、阻尼矩阵C和刚度矩阵K均为66×66对称矩阵。

在支点刚度对系统动力学特性影响分析中，引入支承的当量刚度的概念，即，支承刚度与转子轴段的最小等效刚度的比值，可记为

式中，k为支点某方向上的刚度；ks0为转子轴段的相应方向上的最小等效刚度值。

根据Timoshenko 连续梁理论推导该系统转轴单元刚度特性矩阵，计算转子轴段的三个方向上的最小等效刚度值如表3 所示。给定支点当量刚度，可由式(14)确定支点的支承刚度，表3 给出了当量刚度分别为0.01，0.1，10,100时对应的三个方向上的支承刚度。

2.2 支承特性对系统模态振型的影响

为研究支点支承刚度变化以及支点刚度不对称对转子系统模态振型及其应变能分布的影响和敏感性，分别针对如表4所示的几种不同情况展开讨论：1）两支点完全相同时，两支点的当量刚度k*=k1*=k2*分别选取0.01，0.1，10；2）两支点刚度不对称时，支点1选取固定当量刚度k*=0.001(即支点1 的刚度远小于转轴刚度，小3 个量级，视为弹支)，支点2 的当量刚度k*=k2*分别选取0.01，0.1，10；3）两支点刚度不对称时，支点1 选取固定当量刚度k*=1000(即支点1的刚度远大于转轴刚度，大3个量级，视为刚支)，支点2的当量刚度k*=k2*分别选取0.01，0.1，10。针对如表4所示的支点对称、支点不对称的3类工况，通过仿真分析获得支点刚度、支点不对称对于系统模态振型的影响如图2～图4 所示，图中ω为转速（单位Hz），η为转子的应变能系数，当η小于20%，视为刚体振型；超过20%时认为转子开始出现弯曲振型特征；在η大于80%，认为转子振型完全转化为弯曲振型；η在20%～80%的区域，视为转子-支承的耦合振型。

图2 两支点刚度相同时，支点刚度特性对系统一阶模态振型及应变能的影响Fig.2 When the two fulcrums stiffness are same,the influence of the fulcrum stiffness characteristics on the system first mode shape and strain energy

图3 两支点刚度不对称k1*=0.001时，支点刚度特性对系统一阶模态振型及应变能的影响Fig.3 When the two fulcrums stiffness are asymmetric k1*=0.001,the effect of fulcrum stiffness characteristics on the first mode shape and strain energy of the system

表4 支点刚度特性对系统模态振型影响规律分析Tab.4 Analysis of the influence of the fulcrum stiffness characteristics on the system modal shape

由表4和图2～图4可以看出，随着支点当量刚度k*的增大，系统固有频率增大，转子的弹性应变能系数均呈现不同程度的增大。针对两端支点相同以及两支点不对称的情况（一端弹支k1*=0.001、一端刚支k1*=1000），在支点2当量刚度k2*分别选取0.01，0.1，10时，一阶固有频率增大，转子应变能系数呈增加趋势，转子应变能在系统总应变能中的比重升高，转子一阶模态振型由刚体振型到转子-支承耦合振型再到完全的弯曲振型转化。其中一端弹支的情况，k2*为0.01和0.1，转子的一阶模态振型均表现为刚体振型；而一端刚支的情况，并未出现刚体振型，绝大部分应变能始终在转轴上。

2.3 支承特性对系统模态应变能分布的影响

为进一步分析支点支承刚度变化对转子系统应变能分布的影响，针对如表6 所示的三类不同情况进行分析：(1）两支点完全相同时，两支点的当量刚度k*在0.001 到1000的变化；(2）支点刚度不对称，一端弹支的情况，支点1当量刚度k1*为0.001，支点2的当量刚度在0.001到1000的变化；(3）支点刚度不对称，一端刚支的情况，支点1当量刚度k1*为1000，支点2 的当量刚度在0.001 到1000 的变化。获得支点刚度对转子系统应变能分布的影响如图5所示。

图5 不同工况下，支点刚度特性对转子应变能分布的影响曲线Fig.5 Influence curve of fulcrum stiffness characteristics on rotor strain energy distribution under different working conditions

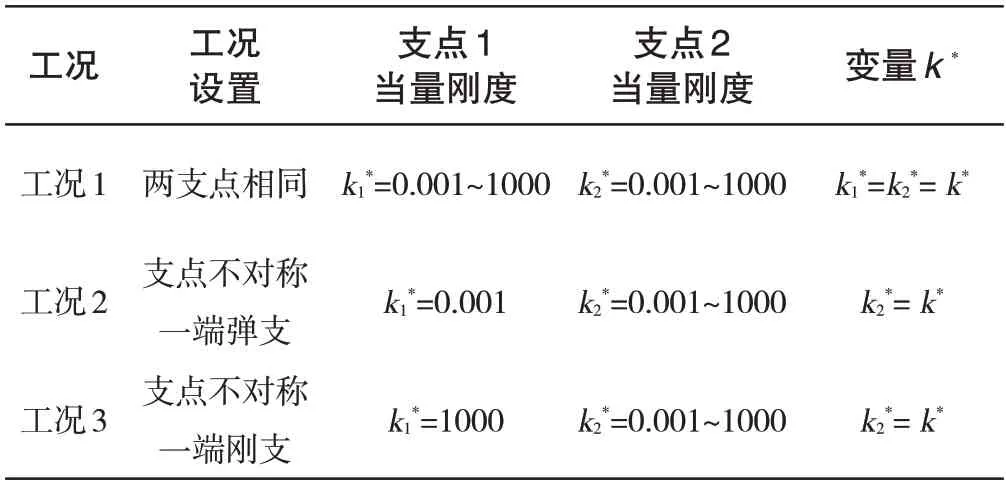
表6 支点刚度对系统模态应变能分布影响规律分析Tab.6 Analysis of the influence of fulcrum stiffness on the modal strain energy distribution of the system

由图5 可以看出：1）两支点相同时，当支点当量刚度k*低于或远低于0.01时，转轴的应变能系数小于20%，即该模态下转轴基本不发生弹性变形，主要变形发生在弹性支承处，对应的模态振型表现为刚体振型。针对两支点不对称，一端弹支的情况，k*在0.001到1的范围内，转子均为刚体模态。然而，两支点不对称一端刚支的情况，没有出现刚体模态；2）两支点相同时，当量刚度k*高于或远高于10时，转轴的应变能系数大于80%，即该模态下主要变形主要分布在转轴上，而弹性支承处基本不发生弹性变形，主要表现为弯曲振型。两支点不对称一端刚支的情况，当量刚度k*大于0.1后，均为弯曲模态，而k*在0.001到0.1范围内，转子应变能系数η在20%～80%的区域，视为转子-支承的耦合振型；3）应变能分布相对于当量刚度k*变化的敏感范围分别为，两支点相同时0.01～10、支点不对称一端弹支时1～100、支点不对称一端刚支时0.001～0.1。

3 结论

本文以两支点转子系统为研究对象，基于旋转梁理论和有限元理论建立了转子系统动力学模型。在此基础上，通过数值仿真分析了支点支承刚度、刚度不对称对转子系统的模态振型及相应的应变能分布的影响规律，得到如下结论：

1）支承刚度特性对转子系统模态振型及其应变能分布有重要的影响。尤其当支承刚度与转子刚度相近时(当量刚度k*在0.1～10的变化范围内)，支承刚度变化对于转子系统动力特性变化非常敏感，系统模态振型和应变能分布随着支承刚度的增减会表现出很大的变化和差异。而当支承刚度较大时(当量刚度k*大于10 时)，支承刚度变化对于转子系统动力特性变化并不敏感，系统模态振型和应变能分布随着支承刚度的增减变化不大。

2）提出的转子的应变能系数η可作为区分系统模态振型的重要参数。当η小于20%，转子基本不发生变形，视为刚体振型；在η超过80%时，变形主要发生在转轴上，可视为完全弯曲振型；η在20%～80%的范围，视为转子-支承的耦合振型。