离心泵用推力滑动轴承的静态特性优化仿真*
2023-11-30侯留凯郝开元
侯留凯 郝开元
(北京航天动力研究所)
0 引言
循环泵是航天器温控系统的唯一动力源,其使用寿命决定了整个温控系统的使用寿命。而轴承作为泵等旋转机械的核心零部件,直接限制了泵单机的使用寿命。我国航天器的循环泵所采用的轴承为滚动轴承,其滚珠会发生物理接触性的摩擦磨损,在连续长时间运行之后,导致轴承失效。目前,泵单机的使用寿命远远达不到航天器长寿命使用的要求,因此通常利用多台泵组备份的方式延长整个温控系统的使用寿命,从而导致温控系统体积过大。因此,有必要将研究目光转向滑动轴承[1-6]。
滑动轴承是一种利用流体(液体、气体)作为润滑剂的轴承,滑动表面被润滑膜分开而不直接接触,在平稳工作过程中不会发生物理接触性的磨损,所以具有极长的寿命、低振动、低噪声等优点[7]。它是基于流体润滑理论原理进行工作的,流体润滑是由一位英国人Tower在1883年发现,Tower 搭建了试验台用以模拟车辆轮轴的滑动轴承润滑状态,发现负载和转速对摩擦系数有很大的影响。当把油滴入滑动轴承中,在滑动轴承中形成的油膜层可以极大地提高轴承的负载能力。后来,Reynolds 提出了流体润滑的微分方程,研究了流体动压润滑产生的原理,这就是著名的雷诺方程,从此为后续的流体动压润滑理论打下了坚实的基础[8-9]。这对后来滑动轴承的研究起到了至关重要的促进作用。
滑动轴承一般分为静压滑动轴承和动压滑动轴承,静压滑动轴承需要一套额外的供油装置,整个装置的体积过大、轴系设计较为复杂。动压滑动轴承是依靠轴承自身结构,在转子达到一定转速时,静止件和旋转件之间形成润滑膜,实现润滑效果[10]。由于航天器温控系统的特殊性,不适宜采用体积过大的静压滑动轴承,而且泵所输送的介质通常为全氟三乙胺、乙二醇等,不能受到外来物质的污染,所以传统的油润滑轴承不适合此类工作环境。只能采用泵内介质自润滑的方式。但是全氟三乙胺和乙二醇的粘度远小于油的粘度,导致轴承的承载力比较低,因此需要对轴承的结构进行优化设计,使得承载力最优化,以满足实际使用需求。这对延长泵单机的使用寿命、减小温控系统的体积具有重要意义。
1 模型建立与理论分析
1.1 轴承的结构及工作原理
推力滑动轴承的结构较为简单,由多个扇形瓦块所构成,瓦块结构常见的结构形式有斜平面-平台式、斜平面式、阶梯式、螺旋槽式及可倾瓦式等[8]。本文所分析的推力轴承结构为斜平面-平台式,如图1 为轴承单个扇形瓦块的结构示意图,扇形瓦块的倾斜区域被称为楔形区域,平坦的区域被称为非楔形区域(轴承的主承载区)。非楔形区域与楔形区域最低点的差值称为楔形进口高度,楔形区域占整个扇形瓦块的比例被称为楔形区域占比。

图1 轴承瓦块结构示意图Fig.1 Bearing pad structure diagram
推力滑动轴承是根据流体润滑理论原理进行工作的,如图2(a)所示,轴承被预先设计成楔形结构,推力盘和轴承之间存在相对运动,在粘性力的作用下,润滑介质由楔形区域的进口方向朝着间隙减小的方向流向出口方向,使得润滑膜形成较大的动压以承受轴向载荷,图2(b)为压力分布示意图,该图仅为示意所用。

图2 轴承工作原理图Fig.2 Bearing working principle diagram
1.2 物理方程建立
1.2.1 雷诺方程
参考以往的文献,本文对推力滑动轴承的分析进行简化,做出如下假设:
1)润滑膜厚度尺寸与径向方向相比尺寸很小,在润滑厚度方向上,压力不发生变化;
2)轴承表面没有相对滑动,遵守无滑移边界条件;
3)轴承表面是纯刚性的,没有发生变形;
4)液体不可压缩,即密度为常数;
关于推力滑动轴承的求解方程在很多文献中已经有了介绍,在此不进行详细推导。根据图1的结构示意图,推力盘和轴承之间的雷诺方程为。
式中,r为推力轴承径向方向坐标,m;h为润滑膜厚度,m;p为润滑膜压力,Pa;θ为推力轴承周向方向坐标,rad;μ为润滑介质粘度,Pa·s;ω为推力盘转速,r/min。
对雷诺方程(1)进行无量纲化处理,定义无量纲参数如下
将公式(2)代入到雷诺方程(1)中进行无量纲化处理,即得无量纲化的雷诺方程
由于雷诺方程为二阶偏微分方程,常采用有限差分法进行求解。将极坐标系下雷诺方程中有关润滑膜压力p和润滑膜厚度h的偏导数采用中心差分法进行离散化处理,用差商代替微分,如下所示(φ即代表润滑膜压力p或润滑膜厚度h):
1.2.2 润滑膜厚度方程
根据图1 和图2,进行推力盘和轴承之间的润滑膜厚度方程推导。润滑膜厚度方程为
式中,HT为推力轴承的楔形进口高度,m;b为楔形区域占比(楔形区域占扇形瓦块的比例)β为轴承扇形瓦块的弧度,rad。
1.2.3 网格划分与边界条件
由于轴承扇形瓦块的结构是对称的,所以在对轴承理论研究时,只需选取其中的一个扇形瓦块作为研究对象,对扇形瓦块划分网格,如图3所示。分别对扇形瓦块的径向方向和圆周方向进行nr+1 等分和nθ+1 等分,因此扇形瓦块的径向方向上有nr+2 个节点,周向方向上有nθ+2个节点。扇形瓦块的边界区域为(0:nθ+1,0)、(0:nθ+1,nr+1)、(0,0:nr+1)及(nθ+1,0:nr+1),扇形瓦块的求解域为(1:nθ,1:nr)。其边界条件为
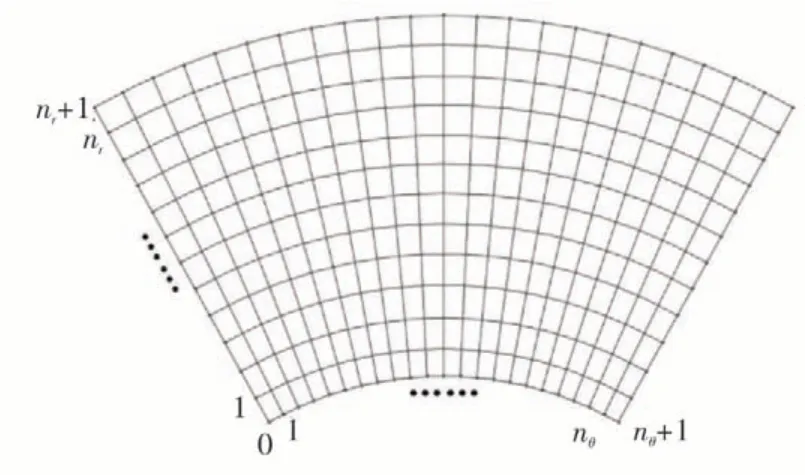
图3 瓦块计算域网格划分示意图Fig.3 Schematic diagram of pad computational domain meshing
1.2.4 轴承静态特性
推力轴承的静态特性主要包括承载力和所受摩擦力矩,分别如下
式中,W为轴承承载力,N;T为轴承摩擦力矩,N·m;N为轴承扇形瓦块数。
1.3 程序计算流程图
雷诺方程为偏微分方程,无法对其进行代数求解。随着计算机技术的快速发展,计算能力得到迅速提高,目前常采用编写计算程序,利用数值计算的方式求解雷诺方程。
本文通过Microsoft Visual Studio 2010 编程平台,利用Fortran编程语言进行程序编制[11-12]。首先给出轴承的结构参数、初始条件及初始的压力分布,求出润滑膜厚度分布,然后更新压力分布,通过压力分布判断压力是否收敛。如果收敛,则输出计算结果,否则重新进行迭代求解,直至收敛。整个求解流程如图4所示。

图4 求解流程Fig.4 Solving process
2 轴承特性数值仿真
轴承性能同轴承的结构参数和润滑膜厚度有很大的关系,因此需要对轴承静态特性进行仿真分析。本文所用润滑工质为50℃的全氟三乙胺,其密度为1.665kg/L,粘度为1.14mPa·s。
2.1 轴承结构参数的影响分析
2.1.1 轴承尺寸的影响
轴承尺寸直接影响轴承轴向受力面积的大小,受力面积和轴承特性密切相关,显然,轴承尺寸越大,其承载力一般也越强。然而轴承的整个外形尺寸受整机整体结构的影响,本文分析所选用的轴承外径为28mm,内径为14mm,稳定工作转速为7500r/min。
2.1.2 扇形瓦块数的影响
选用楔形区域占比为0.5、楔形进口高度为24μm,对不同的扇形瓦块数的轴承进行数值计算仿真,参数如表1所示,结果如图5所示,其中横坐标为推力轴承的扇形瓦块数,纵坐标分别为推力轴承的承载力及摩擦力矩。

表1 推力滑动轴承仿真参数表Tab.1 Thrust sliding bearing simulation parameters

图5 轴承特性随扇形瓦块数的变化关系Fig.5 Bearing characteristics with number of pads
从数值计算的结果可以看出,轴承承载力随着扇形瓦块数的增加,呈先增加再减小的趋势,而摩擦力矩随着扇形瓦块数的增加呈不断增大的趋势。图6分别为扇形瓦块数分别为3,6,10 的推力轴承无量纲压力分布情况,很明显,扇形瓦块数越多,整体压力分布越均匀。把承载力、摩擦力矩及压力分布情况等因素综合分析来看,扇形瓦块数为6是比较好的选择,此时承载力达到最大,而摩擦力矩相对较小,压力分布较为均匀。

图6 不同瓦块数轴承的压力分布图Fig.6 Pressure distribution of with different number of pads
2.1.3 轴承尺寸的影响
选用楔形区域占比为0.5、扇形瓦块数为6 的推力轴承,对不同的楔形进口高度的轴承进行数值仿真,参数如表2所示,结果如图7所示,其中横坐标为推力轴承的楔形进口高度,纵坐标分别为推力轴承的承载力及摩擦力矩。

表2 推力滑动轴承仿真参数表Tab.2 Thrust sliding bearing simulation parameters

图7 轴承特性随楔形进口高度的变化关系Fig.7 Bearing characteristics with wedge inlet height
可以看出,轴承承载力随着楔形进口高度的增加,同样呈先增加再减小的趋势,而摩擦力矩随着楔形进口高度的增加而不断减小。存在一个最佳的楔形进口高度(大约为28μm),使得轴承承载力达到峰值。从压力分布图(图8)上同样可以看出,楔形进口高度为28μm的轴承,承载区域的高压区面积比另外两个楔形进口高度的轴承(分别为10μm和80μm)更大。
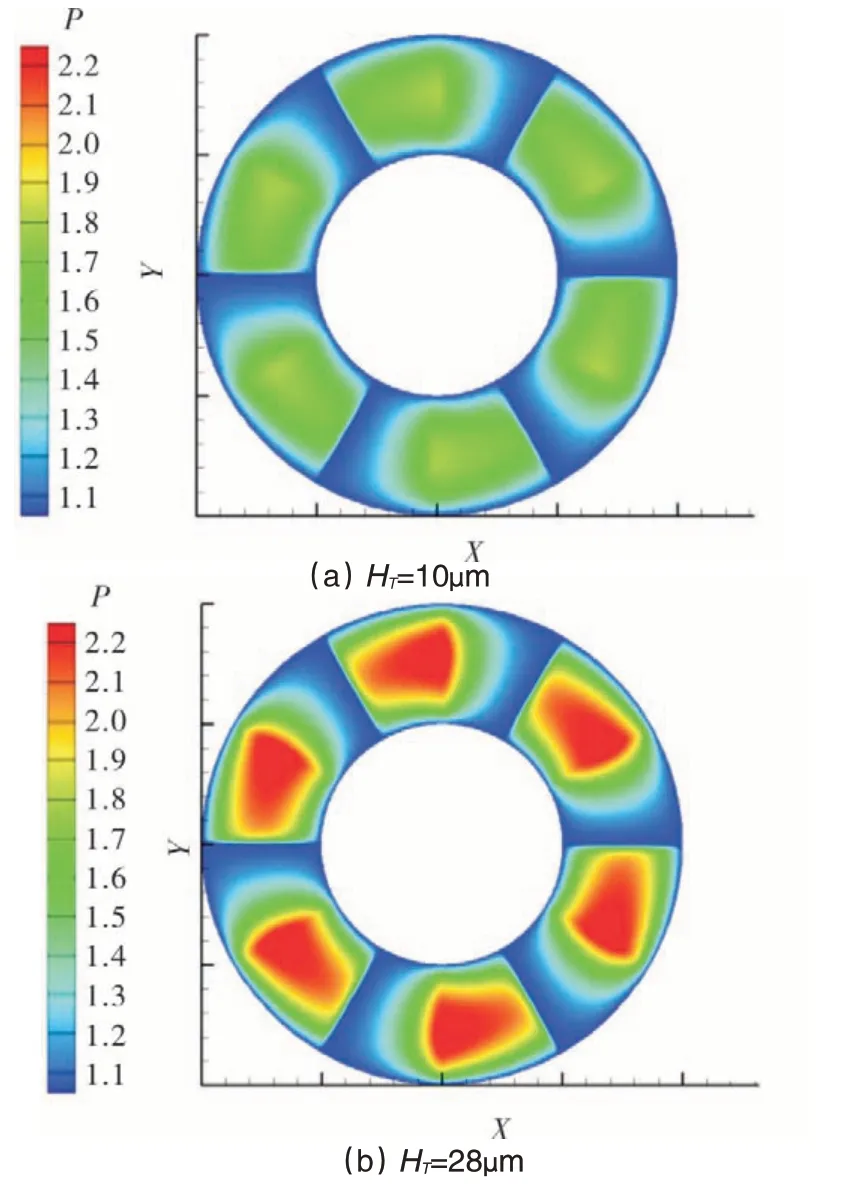
图8 不同楔形进口高度轴承的压力分布图Fig.8 Pressure distribution with different wedge inlet heights
2.1.4 楔形区域占比的影响
选用楔形进口高度为28μm、扇形瓦块数为6的推力轴承,研究静态特性随轴承楔形区域占比的变化关系,参数如表3所示,结果如图9所示,其中横坐标为推力轴承的楔形区域占比,纵坐标分别为推力轴承的承载力及摩擦力矩。

表3 推力滑动轴承仿真参数表Tab.3 Thrust sliding bearing simulation parameters
其关系与楔形进口高度对轴承特性的影响规律类似,在此不做详细叙述。从推力轴承的结构图可知,随着楔形区域占比不断增大,轴承的主承载区域面积不断减小。如图10分别为楔形区域占比为0.2,0.4,0.8时的压力分布图,可以看出,楔形区域占比过小(b=0.2 时)不利于流体动压效应的形成;楔形区域占比较大时,轴承的主承载区域面积较小(b=0.8 时);楔形区域占比为0.4 左右时,此时有利于流体动压润滑效应的形成,高压承载面积较大。

图10 轴承特性随楔形区域占比的变化关系Fig.10 Pressure distribution with different wedge area ratios
2.2 多参数分析
根据2.1 节的分析结果,可以得出各结构参数与轴承承载力和摩擦力矩的关系,而本节主要结合扇形瓦块数、楔形进口高度、楔形区域占比这三大因素,研究其对轴承静态特性的影响。因此,绘制了如图11的“四维图”,三个坐标轴分别代表扇形瓦块数、楔形进口高度、楔形区域占比,颜色代表轴承承载力和摩擦力矩。

图11 多参数分析结果“四维图”Fig.11 Multi-parameter analysis results"four-dimensional map"
根据图11(a)可以看出,图中紫色点的承载较大,扇形瓦块数、楔形进口高度、楔形区域占比过大或者过小都是不合适的。综合来看,扇形瓦块数为5~7,楔形进口高度为20~40μm,楔形区域占比为0.3~0.5 时,轴承承载力处于较高的水平。结合图11(b),发现此时轴承摩擦力矩处于中间范围。因此,可以认为扇形瓦块数为5~7,楔形进口高度为20~40μm,楔形区域占比0.3~0.5为轴承设计的合理结构参数范围。
2.3 润滑膜厚度对轴承特性的影响
推力盘和推力轴承之间的润滑膜厚度,对轴承承载力影响较大。根据以上分析,选用如表4参数的轴承进行数值计算,结果如图12所示,轴承承载力和摩擦力矩均随润滑膜厚度的增加而减小。取轴承的单个瓦块进行分析,如图13所示,当润滑膜厚度为5μm时,瓦块主承载区所形成的压力极大;当润滑膜厚度为30μm时,瓦块主承载区基本上没有形成压力。

表4 推力滑动轴承仿真参数表Tab.4 Thrust sliding bearing simulation parameters

图12 轴承特性随润滑膜厚度的变化关系Fig.12 Bearing characteristics with the film thickness

图13 不同润滑膜厚度的轴承压力分布图Fig.13 Bearings pressure distribution for different film thicknesses
润滑膜厚度过薄,即使轴承承载力较大,其抗冲击能力也较差,推力盘和轴承之间受到冲击作用时,容易发生蹭磨,导致轴承磨损进而失效;润滑膜厚度过厚,无法形成较大的承载力。因此,在进行整机和推力轴承设计时,在满足平衡轴向力的基础上,应使得推力轴承有合适的润滑膜厚度,过薄或者过厚都是不合适的。
3 结论
建立推力轴承的物理模型,基于流体润滑理论的雷诺方程、润滑膜厚度方程,给出了数值仿真的计算流程,编写推力轴承静态特性的数值计算程序。
选用内径为14mm、外径为28mm的推力轴承进行数值仿真分析,发现轴承的结构参数对轴承特性影响较大,存在最佳的扇形瓦块数、楔形进口高度和楔形区域占比,使得轴承承载力达到最大,摩擦力矩相对较低。选用6个扇形瓦块、楔形进口高度为28μm,楔形区域占比为0.4的推力滑动轴承,对不同润滑膜厚度的轴承进行数值仿真,轴承承载力和摩擦力矩均随着润滑膜厚度的增加而不断减小。
因此,在推力滑动轴承设计过程中,需对轴承的结构进行优化设计以达到最佳的性能,以防止出现因承载力不足导致轴承失效的状况。同时需注意保证合理的装配间隙,使轴承有较合适的润滑膜厚度,以达到最佳的工作状态。
