基于数学形态学的零样本低照度图像特征增强方法

杜兵芳

(重庆外语外事学院 国际商贸与管理学院,重庆 400065)

数字图像信息含量丰富,高品质图像是高质量使用图像的先决条件。零样本低照度图像通过一系列图像处理方法可提升图像的质量和细节,进行图像特征增强,使图像更加清晰、明亮[1-2]。江泽涛等[3]提出了基于潜在低秩表示与复合滤波的红外与弱可见光增强图像融合方法:使用高动态范围压缩增强法,提高可见光图像的亮度;利用复合滤波分解法对红外图像进行分解,获取图像低频和高频层;通过加权最小二乘法增强图像特征,以线性叠加的方式得到融合图像。但该算法图像增强所用时间较长,存在图像处理效率较低的问题。徐少平等[4]提出了采用深度学习与图像融合实现策略的低照度图像增强算法:使用照射分量预测模型对输入的低照度图像进行快速估计;在Retinex模型框架下结合最佳照射分量结果生成适度曝光阈值;采用局部结构化融合法和利用色度加权融合机制来融合图像,最终获取增强图像结果。但该算法得到的最佳照射分量结果的平均绝对偏差有待进一步验证,存在图像增强精度较低的问题。Al Sobbahi R等[5]提出了集成图像增强和分类的微光同态滤波网络方法:构建微光同态滤波网络模型,在模型中训练图像增强和分类性能,以获取图像增强频率滤波,完成集成图像增强。但该算法计算过程较复杂,存在计算力较差的问题。

数学形态学是一种基于集合论和拓扑学的图像处理,通过对图像中的形状、结构和空间关系进行分析和变换,实现图像特征提取、去噪和增强等目的。数学形态学具有较强的非线性处理能力和形态特征保持能力,能够更好地适应不同场景下的图像处理需求。基于此,本文提出一种基于数学形态学的零样本低照度图像特征增强方法。该方法使用超像素合成的高质量正常曝光图像作为参照图像,以提供去噪预处理的优化依据;采用半软阈值指数衰减法对低照度图像进行小波去噪以减少图像中的噪声干扰,利用膨胀和腐蚀操作提取低照度图像中的特征结构元素以辅助后续图像增强处理,应用盒式滤波技术求解低照度图像的积分反射分量以增强图像的亮度和对比度;通过全局零样本迭代学习增益方法对低照度图像进行特征增强处理,最终达到改善低照度图像的细节和视觉效果的目的。下面在此主旨范围展开相关讨论。

1 数学形态学的零样本低照度图像特征增强

1.1 零样本低照度图像与图像特征

零样本是指在训练阶段没有相应的图像样本数据用于处理和学习,后续的计算机图像处理难度较大。低照度图像是在光线较暗环境下拍摄的图像,会受到噪声、细节模糊等问题的影响,图像的细节信息被破坏,噪声大、亮度不均匀、色彩失真。

图像特征是图像中能够辨识局部或全局的特征信息,增强图像特征可以改善图像的清晰度、亮度、颜色等。其实现途径可以采用超像素合成的参照图像作为零样本,使用半软阈值指数衰减法对低照度图像进行去噪预处理;运用膨胀和腐蚀操作来提取低照度图像的特征结构元素,利用盒式滤波法求解低照度图像的积分反射分量,由此实现增强低照度图像的信息特征。

1.2 数学形态学要述

数学形态学是一种图像处理和分析的数学理论,该理论主要关注图像的形状、结构和拓扑特征。它使用一系列的基本形态学操作,如膨胀、腐蚀、开运算、闭运算等,改变和提取图像中的形状和结构信息。通过结构元素与图像进行局部区域的匹配和变换,提取图像中的关键形状特征,从而实现图像的深入处理。具体的形态学操作如图1所示。

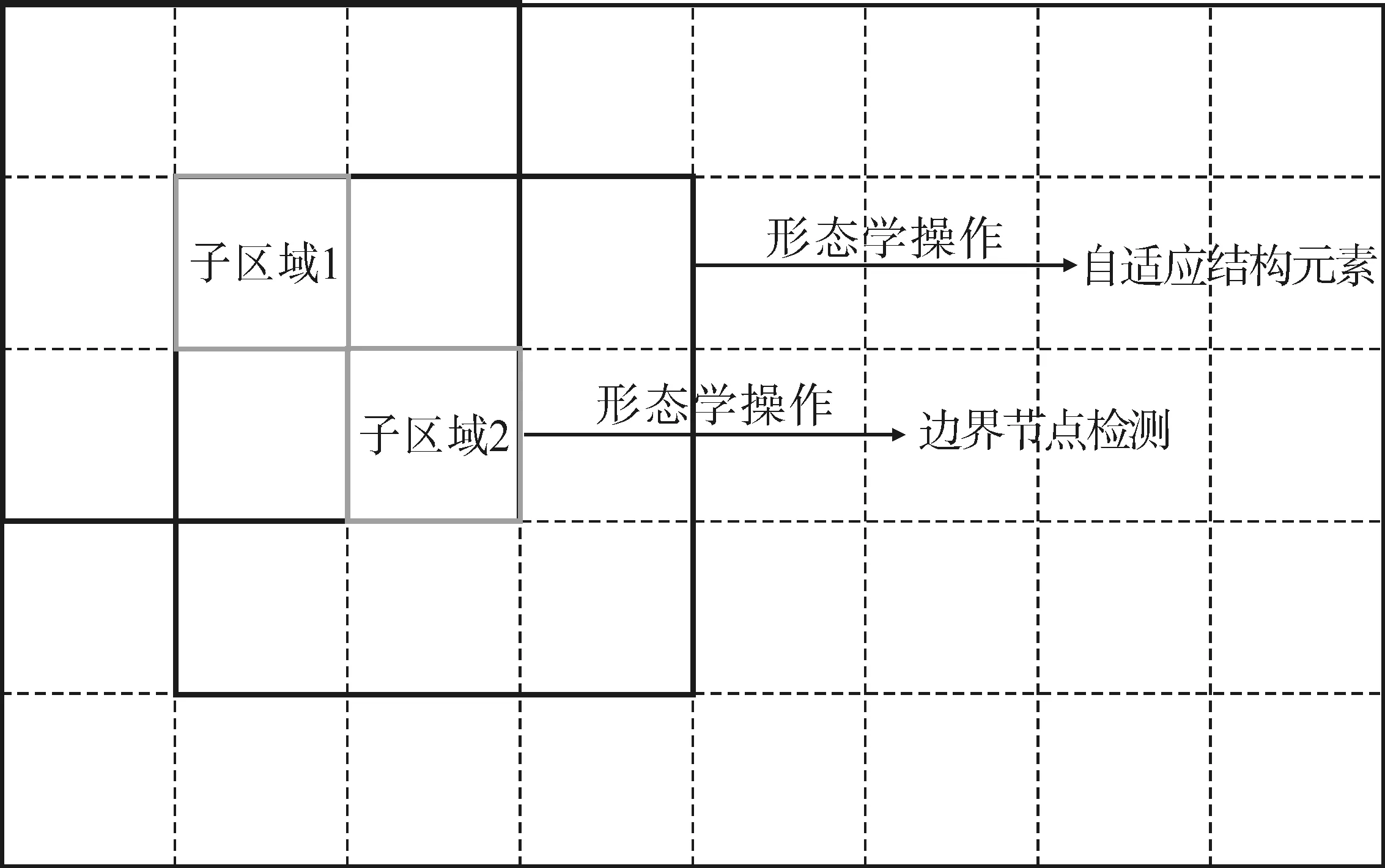
图1 数学形态学操作示意

数学形态学操作(如膨胀和腐蚀)具有很好的形状保持性能,可在保持目标形状的同时改变其大小和位置,通过选择合适的结构元素来适应不同尺度的图像。另外,可以提取图像中边缘、角点、凸壳等结构信息,这些信息对于图像特征增强和模式识别具有重要作用。同时,可以解决低照度图像特征增强过程中的对比度增强、边缘增强、细节增强等问题,如开运算和闭运算操作可以改善图像对比度,突显图像细节。

数学形态学能够提取图像中的目标区域,分析和描述图像中的物体形状和结构特征,能够应用于计算机视觉、医学图像处理、数字图像修复等领域的目标检测、图像增强、特征识别等,为图像处理和分析提供有效途径,在处理低照度图像时具有较好的灵活性和适应性。

1.3 低照度图像的超像素合成

在构建低照度图像特征增强模型时,需要将高质量的正常曝光图像作为参照图像进行零样本学习,所以需要对低照度图像进行超像素合成,以其作为图像特征增强的训练基准。采集一组单反摄像机拍摄的图像,图像内容应涵盖丰富的场景和各种不同的光照条件。为了使所有图像均满足低照度图像增强的参考图像需求,要综合考虑亮度、颜色、细节等因素[6]。采用超像素划分方法将图像细分为多个子区域,数量通常在300～480之间。这些子区域不仅需要保留图像的亮度、颜色、细节等有效细节信息,同时还应避免破坏原始图像的边界信息。计算各像素块在原始图像中对应的颜色平均值:

(1)

1.4 低照度图像去噪预处理

上述低照度图像超像素合成数据集中含有大量噪声干扰,不利于后续特征增强。因此,利用小波分解对低照度图像进行去噪预处理。传统的小波去噪法对图像信号的处理主要通过小波软阈值和硬阈值实现,但是小波软阈值和硬阈值对于信号的衰减处理过强,容易导致低照度图像关键特征损失[7-8]。对此,使用半软阈值指数衰减法优化小波去噪,去除小波分解降噪过程中产生的平滑加性噪声。设定低照度图像信号像素值为b,阈值为μ1、μ2,当μ2<|b|时,阈值参数与硬阈值相近,当μ1<|b|≤μ2时,阈值参数与软阈值相近。半软阈值函数如式(2)所示:

(2)

通过对μ1<|b|≤μ2的线性变换,可以有效减缓低照度图像中信号的衰减,避免加性噪声引发的低照度图像细节损失。在对加性噪声展开处理后,还要考虑乘性噪声对低照度图像清晰度的影响。引入奇异值算法对低照度图像展开去噪处理。设g(t)在像素点上的Hausdorff奇异指数为i(t),则拥有与其相同奇异数值t的点集合为F(t),F(t)的计算公式为式(3):

F(t)=[t:i(t)=i]

(3)

为计算退化的奇异过程,以β半径的i区域奇异点为参考,计算公式如式(4):

F′(t)=[t:i(t)-β≤i(t)≤i+β]

(4)

引入Hausdorff维度的dimⅡE算法,设o为维数,并用|Eo|l<0<∞表示E的o覆盖,可推导出式(5)。

(5)

将式(4)与式(5)结合,得到多重分形度的低照度图像局部奇异谱,使其在不破坏图像细节清晰度的前提下对低照度图像内的不规则信号展开平滑处理,达到去噪目的。输出去噪后的低照度图像,为后续图像特征提取提供数据保障。

1.5 低照度图像特征提取

数学形态学特征提取算法具有图像特征边缘提取光滑的特点,因此利用数学形态学方法提取上面去噪后的低照度图像特征。数学形态学是以集合论为基础的图像分析方式,主要是对图像中的元素进行结构化检测,通过追踪像素点的位移变化完成结构元素定位,基本形态变换包括腐蚀、膨胀、开运算和闭运算。将低照度图像边缘特征作为追踪结构元素,通过膨胀和腐蚀处理,提取结构元素,膨胀的数学表达式为:

I⊕P={A|I(S+D,F+G)∪P(D,G)}

(6)

式(6)中,I为去噪后图像;P为边缘特征结构元素;⊕为膨胀运算;D、G为水平和竖直方向的最大位移;S、F为特征像素点位置;A为膨胀后的灰度级。腐蚀处理即为膨胀的逆向表达:

IΘP={A|I(S+D,F+G)∪P(D,G)}

(7)

式(7)中,Θ为腐蚀运算。对低照度图像进行腐蚀处理,标记图像边缘特征具体走向,有序扩展特征结构元素相关属性,突显细小特征。

通过膨胀和腐蚀运算提取低照度图像特征结构元素,将其设定为p1和p2,对应I1、I2子集,则会产生以下情况:

if→P=P1+P2

I1⊕P=I2⊕(P⊕P2)=(I⊕P1)⊕P2

(8)

if→I1⊆I2

I1⊕P⊆I2⊕P,I1ΘP⊆I2ΘP

(9)

IS⊕P=(I⊕P)S

ISΘP=(IΘP)S

(10)

式(8)表示不同特征结构元素的结合,较小特征可能会连接成较大特征结构元素。公式(9)表示较小特征具有递增性,会由较小特征结构变为较大特征结构。公式(10)表示特征不具备变形。至此,通过对低照度图像的膨胀、腐蚀处理,实现图像特征发展形式判断,完成图像特征结构元素提取。

1.6 低照度图像特征结构元素增强

根据低照度图像中不同颜色通道的比例关系构建颜色损失函数,解决图像颜色失真的问题。利用公式(11)计算低照度图像在RGB色彩空间内的像素对应权值:

ωi(x,y)=εm{log[δm·dimⅡE+(P2P2)]}

(11)

式(11)中,εm为颜色恢复系数;δm为颜色调节参数。为了确保颜色不出现失真,减少对原始光照条件依赖,则优化原始颜色损失函数为:

(12)

式(12)中,d(m)为低照度图像分辨率;I(x,y)为颜色像素补偿系数;λ为颜色比重,λ取值越大表明颜色分布越平均,能够有效改善图像灰暗区域像素过增的问题。

若处理窗口半径取值较大或者分辨率较大的低照度图像,算法所花费的时间会明显增加。为解决此问题,则采用盒式滤波展开运算,求解低照度图像积分反射分量结果:

E(x,y)=logκH(x,y)-log[H(ω)δk]

(13)

式(13)中,H(x,y)为盒滤波函数,δk为低照度图像的灰度熵;κ为低照度图像的平均亮度值。在判定低照度图像达到均值化处理后,将公式(13)中的积分反射分量应用到低照度图像零样本加权学习中,低照度图像单尺度线性加权函数表达式为:

(14)

式(14)中,D为尺度参数的取值范围;V为熵值。采用零样本方法对低照度图像单尺度线性加权函数展开增强处理[9],获取不同场景的光照分量估计值,进而构建光照分量集合,增强低照度图像特征。将颜色空间由RGB转换到HSI,通过全局零样本迭代学习增益函数调节低照度图像亮度,在HSI空间内对低照度图像颜色展开恢复处理,增强低照度图像特征结构元素:

S(x,y)=ψpν(x,y)

(15)

综上,式(15)中,ψ为边缘梯度,完成了对低照度图像增强处理。具体图像特征结构元素增强处理流程如图2所示。

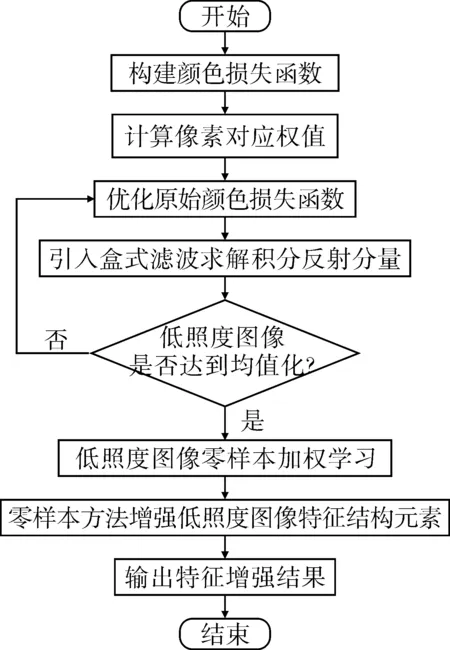
图2 图像特征结构元素增强流程图

2 测试与分析

测试图像为某小区监控摄像头拍摄的可公开画面图像,涵盖不同的场景和物体。从在夜晚或阴天环境下拍摄的图片中随机选取了5000个低照度图像作为训练样本,1000个低照度图像作为测试样本。这些低照度图像的分辨率均为320×320,呈现曝光不足、对比度低、噪声较大、细节丢失等原始状况。

为了进一步验证本文所述方法(基于数学形态学的零样本低照度图像特征增强方法)的图像特征增强有效性,在此与文献[4]方法(采用深度学习与图像融合混合实现策略的低照度图像增强算法)和文献[5]方法(集成图像增强和分类的微光同态滤波网络)进行对比分析。对比内容为峰值信噪比、图像失真系数、准确性等。采用文献[4]、[5]和本文所提的3种方法将获取的1 000幅低照度图像进行增强处理。通过峰值信噪比(PSNR)衡量3种方法去噪处理后的低照度图像质量,PSNR越高表明特征增强后的低照度图像清晰度越高。详细的测试结果如表1所示。

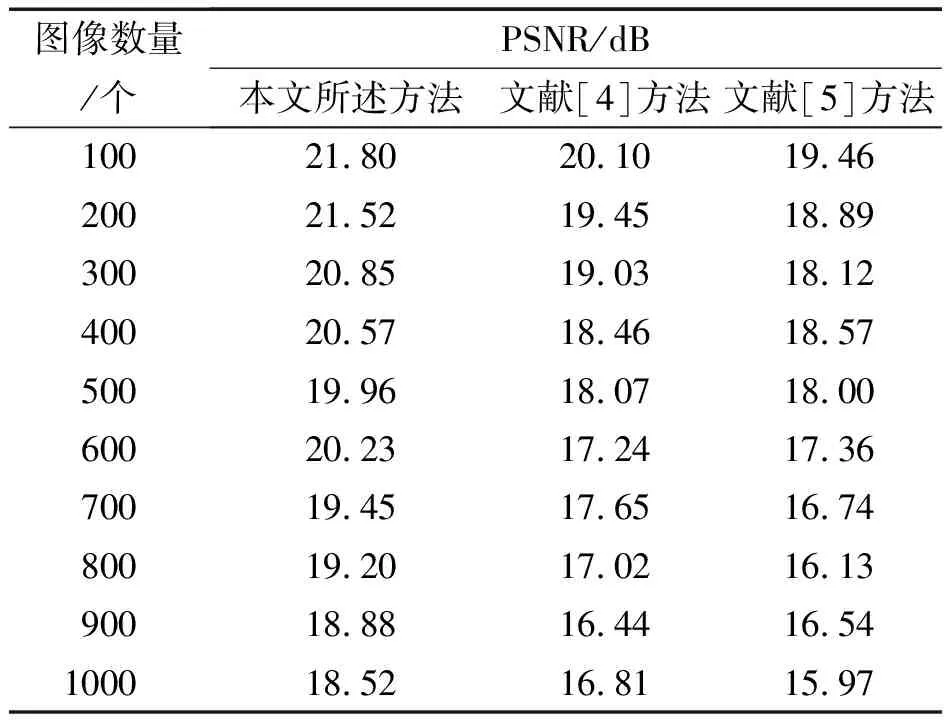
表1 3种方法下的PSNR值测试结果

由表1可知,随着图像数量的持续增加,3种方法下的PSNR值呈直线下降趋势。在处理完全部低照度图像时,本文所述方法的PSNR值为18.52dB,文献[4]和文献[5]方法的PSNR值分别为16.81dB、15.97dB。对比结果可知,本文所述方法的PSNR值明显高于其它两种方法。由此说明,本文所述方法特征增强后的图像质量较好,图像更清晰自然,验证了本文所述方法的比较优越性。

为进一步地客观评价3种方法,引入特征增强后的图像亮度失真系数(LOE)作为评价指标。对图像特征增强效果而言,LOE的值设为QLOE,其越小,亮度自然性保持越好、亮度失真率越低。LOE计算公式为:

(16)

式(16)中,m为低照度图像中的像素个数;RD(x)为原始低照度图像与增强后图像的相对阶差分。据此计算3种方法下的LOE,3种方法下的亮度失真结果如表2所示。

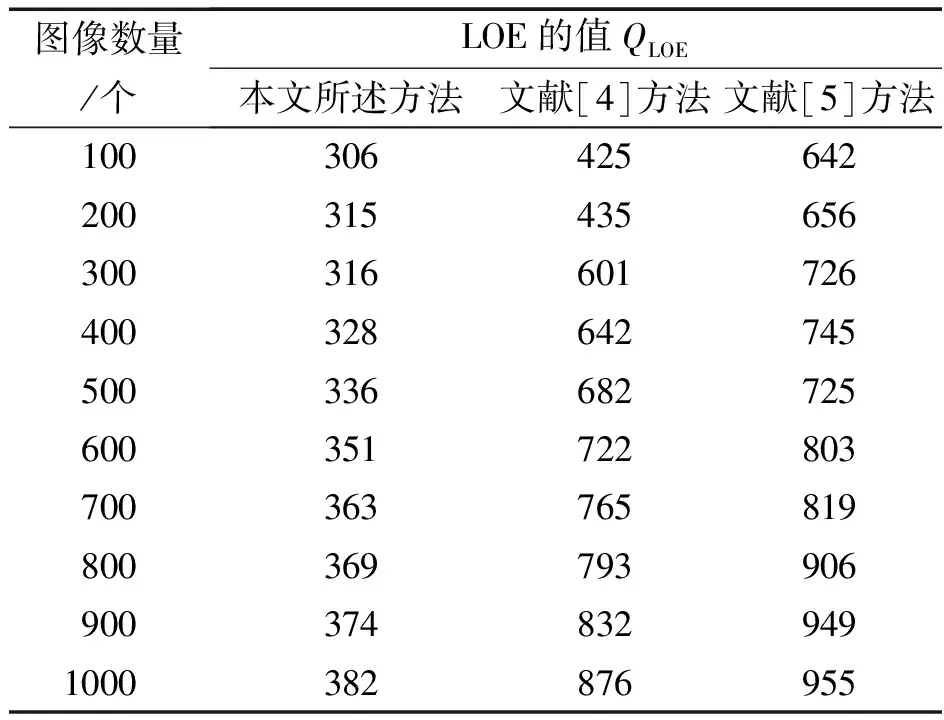
表2 3种方法下的LOE值测试结果

由表2可知,本文所述方法针对所有低照度图像特征增强处理后,图像失真系数均控制在400以内。而文献[4]方法的图像失真系数在400～900范围内,文献[5]方法的图像失真系数超过900。因此,由测试结果说明本文所述特征增强方法的亮度失真系数最低,图像经过本文所述方法处理后的亮度特征自然性保持良好,进而有效地控制了亮度失真率。

使用相同的测试数据集,按照随机化处理顺序重复测试峰值信噪比和图像失真系数300次。将每次测试得到的评价指标计算结果进行平均值计算,以获取图像处理准确性评估结果。3种方法下的低照度图像增强准确性结果如图3所示。

根据图3,本文所述方法通过膨胀操作将结构元素与低照度图像的像素进行比较并更新像素值,利用腐蚀操作标记图像边缘特征具体走向,突显细小特征,以此提高低照度图像的增强效果,低照度图像增强准确性达97%,高于文献[4]和文献[5]两种方法,具有较好的实用性。

3 结语

数学形态学作为一种基于拓扑结构的图像处理方法,能够有效地增强目标特征及改善图像质量,相比传统的滤波和增强方法,具有较强的非线性处理能力和形态特征保持能力,更好地适应了不同场景下的图像处理需求。本文基于数学形态学研究了零样本低照度图像特征增强方法,通过对低照度图像结构元素的形态学运算,以期增强低照度条件下的图像特征,准确地获取图像中的细节信息,提高图像的可视化质量和识别性能。该方法可以在没有任何样本的情况下对低照度图像进行增强,相比于传统增强方法,能够更好地保留图像的细节信息,并具有较好的适应性和准确性。但是,在形态学运算过程中需要注意结构元素的合适度,根据极端低照度条件进行调整和优化,以期提高形态学运算效果,进一步改善处理后的图像质量。