随机环境中加权分枝过程的偏差不等式

鲁 展,彭 聪,邓 琳

(长沙理工大学 数学与统计学院,湖南 长沙 410114)

加权分枝过程(Weighted branching processes,WBP)由Rösler[1]于1992年引入,可视为经典分枝过程(Galton-Watson, G-W过程)一个推广。2004年Kuhlbusch[2]首次在加权分枝过程中引入随机环境。随机环境加权分枝过程具有自相似结构、分枝结构和乘法结构。若给每个个体一个抽象的权重,权重非负条件下的随机环境加权分枝过程也可以称为Mandelbrot’s cascade[3-4]。目前关于随机环境加权分枝过程的灭绝问题和条件极限定理的研究成果较丰富,如文献[5,6]。

在概率不等式的相关研究中,1963年Hoeffffding[7]给出了有界随机变量之和的概率不等式,2006年Nagaev[8]研究了临界G-W过程的概率不等式。Fan等[9-10]2013年在Bernstein条件下证明了鞅的大偏差展式,2020年又建立了随机环境分枝过程的一致Cramer中偏差。但值得注意的是,关于随机环境加权分枝过程的概率不等式研究甚少,因此本文将在随机环境分枝过程概率不等式研究的基础上,尝试借助Bernstein不等式得到随机环境中加权分枝过程的偏差不等式。

1 模型引入

在独立同分布的随机环境ξ=(ξ0,ξ1,…)中,加权分枝过程{Yn}定义如下:

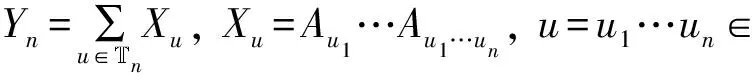
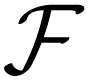
2 基本结果及证明

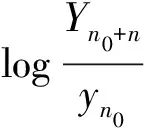
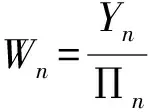
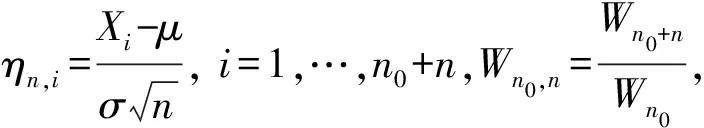
基于以上定义,有

(1)

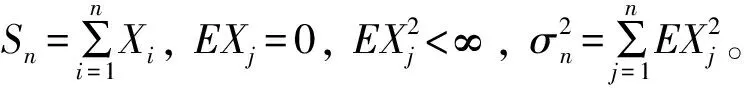
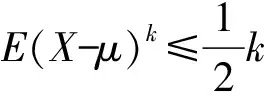
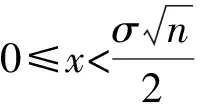
(2)

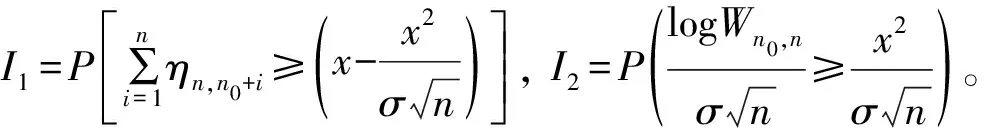
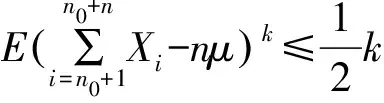
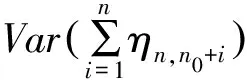
(3)

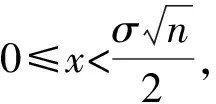
(4)

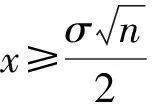
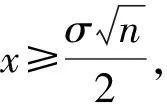
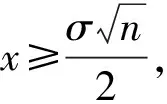
定理1得证。