考虑分布式电源接入的配电网多目标优化重构方法研究

王星海，李 鑫，王世坤，王月茹，梅永超

（国网山东省电力公司淄博供电公司，山东 淄博 255000）

0 引言

配电网通常情况下闭环设计、开环运行，网络结构呈辐射状。配电网的各支路中含有大量的分段开关和联络开关，调度员可以根据运行需求来调整分段开关和联络开关的运行状态，主要包括正常运行状态下的优化重构和故障状态下的快速恢复重构［1-3］。

近年来国内外学者对配电网优化重构进行了大量研究，取得了一系列的研究成果。配电网优化重构目标方面，最常用的目标有：降低配电网网络损耗［4］、提高电压质量［5］、均衡线路负载［6］或综合考虑多个目标［7］，但对于多目标优化重构问题中目标函数权重系数的确定方法都未涉及。求解配电网重构主流的算法包括模拟退火法［8］、遗传算法［9］、粒子群算法［10］、蚁群算法［11］、萤火虫算法［12］、混合算法［13］等，目前遗传算法的应用较为普遍，但存在解的数量组合呈爆炸式、搜索效率低的问题。分布式电源（distributed generation，DG）渗透率的逐步提高，使配电网的供电方式由单电源辐射状供电转变为多电源联合供电，供电方式的转变使得配电网的优化重构更为复杂［14-15］。在分布式电源的处理方式上，大部分研究将其视为PQ 型［16］分布式电源来处理，对于分布式电源的不确定性和波动性对配电网重构的影响分析不够全面和深入。

提出一种考虑分布式电源接入的配电网多目标优化重构方法。该方法的综合目标函数包括四部分：降低网损、均衡负载、提高电压质量、减少开关操作次数。应用层次分析法确定目标函数各部分的权重系数，通过确定目标层、准则层与方案层，构建层次结构模型，科学地确定目标函数各部分的权重系数；考虑DG 接入的影响，采用改进的遗传算法作为优化算法，搭建配电网优化重构决策支持系统架构，既满足配电网静态优化重构的需求，又能实现故障状态下的快速恢复重构。利用MATLAB 对IEEE 33节点系统算例搭建仿真模型，仿真结果验证算法的正确性。

1 含DG的配电网优化重构模型

1.1 目标函数

配电网优化目标包括降低网损、均衡负载、减小电压偏差，除此之外，目标函数还考虑了减少分段开关和联络开关操作次数。操作开关会带来短时停电，影响电力用户用电体验，产生一定的经济损失；开关操作次数的增加还会降低使用寿命、增加人力投入、带来安全隐患等。因此，目标函数为降低网损、均衡负载、提高电压质量与减少开关操作次数。

1）降低网损。

式中：f1为目标函数的网损部分；N为支路总数；i为支路编号；Vi、Ri分别为末端电压、线路阻抗；Pi、Qi分别为有功功率、无功功率；ki为支路分段开关或联络开关的通断状态，ki=0 表示断开，ki=1 表示闭合［17］。

2）均衡负载。

式中：f2为目标函数的均衡负载部分；Ii、Iimax分别为流过支路i的实际电流、最大允许电流。

3）提高电压质量。

式中：f3为目标函数的电压质量部分；j为节点编号；n、Vj和VjE分别为配电网节点总数量、节点j的电压和节点j的额定电压。

4）减少开关操作次数。

式中：f4为目标函数的开关操作次数部分分别为支路i重构前后的开关通断状态，取值为0 表示断开，取值为1 表示闭合。

1.2 约束条件

在配电网优化重构过程中，需要满足约束条件如下。

1）潮流平衡约束，即全网功率平衡；

2）支路容量约束，即重构后各支路上的功率不允许超过限定值，设Si为支路i的功率为支路i的最大允许容量，则支路容量约束为

3）网络拓扑约束，根据配电网的运行特点，优化重构后的网络拓扑要满足既不出现孤岛也不出现环网的要求；

4）节点电压约束，要保证重构后的配电网各节点电压不越限，设分别为节点j的电压上下限，则节点电压约束为

5）DG 功率约束，要保证重构后的配电网各DG的有功功率和无功功率在允许的范围内，设PDGj、QDGj分别为节点j的DG 有功功率和无功功率分别为节点j的DG 有功功率的上下限分别为节点j的DG 无功功率的上下限，则DG 功率约束为：

1.3 分布式电源潮流计算模型

DG 接入配电网进行潮流计算时，通常可以等效为PQ 节点、PV 节点或PI 节点进行处理［18］。

1）PQ 节点。等效为PQ 节点的DG 可以简单理解为其输出的有功功率和无功功率是不变的，因此可以处理为“负的负荷”，通常来说，风机、汽轮机、内燃机等类型的DG 可以当作PQ 节点来处理。

2）PV 节点。PV 节点可以认为输出恒定的有功功率且节点电压始终保持不变，微型燃气轮机、采用电压控制策略的光伏电池、燃料电池等可以等效为PV 节点进行处理。

3）PI 节点。PI 节点可以看作输出的有功功率恒定，且流过节点的电流保持不变，采用电流控制策略的光伏电池、储能系统等通常可以等效为PI 节点进行处理。

1.4 归一化处理

考虑到四部分目标函数量纲的不同，选取minmax 方法，对四部分目标函数进行归一化处理。

将四部分目标函数进行处理后，可得到最终的目标函数为

式中：a、b、c、d分别为目标函数降低网损、均衡负载、提高电压质量、减少开关操作次数的权重系数。

2 层次分析法确定目标函数权重系数

层次分析法是一种常用的权重决策分析方法，通过目标、准则、方案等层次，将定性问题转化为定量问题进行分析。选取层次分析法来计算目标函数各部分的权重系数［19］。

2.1 建立层次结构模型

建立层次结构模型是评估权重系数的核心步骤，该指标体系包含了三层。

目标层：目标层为各层指标的最终反映，文中的目标层选为配电网优化运行A。

准则层：综合考虑影响配电网优化运行的因素，将目标展开研究，形成评估目标层的准则，包括安全效益B1、用户效益B2、社会效益B3、经济效益B4。

方案层：于文中研究而言，为了实现目标可选的备选方案包括了降低网损C1、均衡负载C2、提高电压质量C3、减少开关操作次数C4。

配电网重构目标函数层次结构模型如图1 所示。

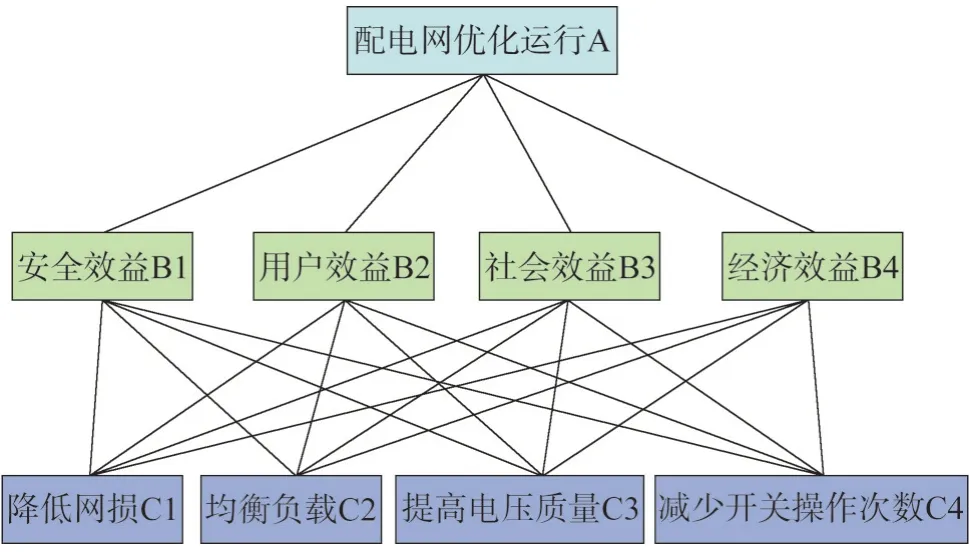
图1 配电网重构目标函数层次结构模型Fig.1 Hierarchical structure model of objective function for distribution network reconfiguration

2.2 构造判断矩阵并计算权重系数

判断矩阵的含义是：相对于上一层次指标，本层次中有关指标的相对重要程度。通过对同一层次中的因素两两对比，按照重要性进行等级评定，从而实现由定性向定量的转化，两两比较的结果构成判断矩阵。采用1—9 标度法［20］来确定判断矩阵，各级标度含义如表1 所示。

表1 1—9标度法含义Table 1 Meaning of 1-9 scale method

采用专家打分的方式，确定各层次的判断矩阵，并采用yaahp 软件进行数据分析，得出综合目标函数的各层权重系数和一致性判断结果如下。

以A-B 的计算为例，判断矩阵为

计算可得，上述判断矩阵符合一致性检验结果，A-B 的权重系数为[ 0.49 0.13 0.23 0.15 ]。

同理，B1-C 的判断矩阵为

B2-C 的判断矩阵为

B3-C 的判断矩阵为

B4-C 的判断矩阵为

上述判断矩阵经验证均满足一致性检验要求，根据yaahp 软件计算结果可得，方案层中目标函数四部分的权重为：a=0.353 0、b=0.254 7、c=0.221 3、d=0.171 0。

3 配电网优化重构决策支持系统

为将上述数学模型转化为实际应用，开发了配电网优化重构决策支持系统，系统架构分为展示层、服务层与数据层，如图2 所示。

图2 配电网优化重构决策支持系统架构Fig.2 Architecture of decision support system for distribution network optimization and reconfiguration

根据配电网优化重构流程，将展示层设计为三个模块：

1）数据采集模块。用于采集配电网、DG 及负荷的各类数据，如有功功率、无功功率、电压、开关状态及网络拓扑结构等，并将数据上传于后端服务器，作为优化重构算法的数据来源。

2）参数设置模块。用于设置优化算法的相关参数，包括了四部分目标函数的权重系数a、b、c、d的设置，通过设置四个权重系数的不同大小，可以决定优化的方向，从而得到不同的优化结果；参数设置模块还可以设置某一个或几个开关状态为指定状态，不参与优化过程中的状态变化，该功能可应用于配电网故障时的恢复重构。

3）结果输出模块。用于输出配电网优化结果，包括优化后的开关状态、配电网拓扑结构、功率及电压等，还包括了目标函数网络损耗、电压偏差、开关操作次数等。

4 求解优化模型的改进遗传算法

遗传算法是一种通过模拟生物自然进化过程，从而实现最优解搜索的人工智能优化算法，基本操作有选择、交叉和变异，编码方式有二进制和十进制，文中选用最常见的二进制编码方式。

4.1 基于环路的交叉和变异算子

遗传算法进行配电网重构的难点之一在于解的数量组合呈爆炸式，且交叉和变异过程中会产生大量的不可行解，导致寻优效率降低。为尽量减少交叉和变异过程中不可行解的产生，文中采用基于环路的方式，具体方法如下：

1）假设配电网中所有的分段和联络开关均闭合，从而找出网络中所有的环路；

2）对于交叉算子而言，选择需要进行交叉的两条染色体，随机选取一个有且仅有一个开关断开的环路进行交叉，可以保证交叉后子代染色体中断开开关的总数不变，从而大大减少了孤岛和环网的产生，不可行解的数量将大幅降低；

3）对于变异算子而言，同样选取有且仅有一个开关断开的环路进行单点变异，也可以大幅降低不可行解的数量。

4.2 算法流程

基于改进的遗传算法，配电网优化重构算法步骤如下：

1）生成初始种群，对初始种群进行适应度函数计算；

2）选择、交叉与变异。选择操作采用轮盘赌选择方式，结合精英保留策略；交叉和变异操作的位置由随机数确定，经过交叉和变异之后可以产生新的个体；

3）可行解校验与再选择。经过交叉、变异后产生的新个体中会有大量的不可行解，需要对新个体依次进行可行性校验，及时淘汰不可行解，根据淘汰的不可行解的数量从附带种群中进行二次选择，保证种群数量充足；

4）计算种群个体的适应度，并判断是否达到最大进化代数，若是，则输出优化结果，若否，则返回步骤2）。

遗传算法优化流程如图3 所示。

图3 遗传算法迭代流程Fig.3 Flowchart of genetic algorithm iteration

5 算例分析

5.1 仿真系统与参数

以IEEE 33 节点配电系统为例，采用MATLAB为操作语言，设定系统标准电压为12.66 kV，电源节点电压标幺值为1，文献［21］给出了线路阻抗及节点负荷情况，设置遗传算法种群数量为50，最大迭代次数为100，节点和支路编号如图4 所示，图中黑色数字代表节点编号，红色数字代表支路编号（对应分段开关和联络开关）。

图4 IEEE 33节点配电系统Fig.4 IEEE 33 node distribution system

5.2 静态重构结果分析

为了验证文中方法的正确性，利用MATLAB 分别对不同算例进行了仿真分析，首先在不考虑DG接入的情况下，设置了4 个算例。

算例①：系统重构前。

算例②：网损最小单一目标函数重构，即通过参数设置模块使权重系数满足a=1、b=0、c=0、d=0。

算例③：电压质量最高单一目标函数重构，即设置权重系数满足a=0、b=0、c=1、d=0。

算例④：文中提出的多目标函数重构，仿真算例中权重系数的设置为a=0.353 0、b=0.254 7、c=0.2213、d=0.171 0。

仿真结果如表2 和图5 所示。

表2 不同算例仿真结果Table 2 Simulation results of different examples

图5 不同算例对应的节点电压幅值Fig.5 Node voltage amplitude corresponding to different calculation examples

从表2 和图5 可以看出，采用文中的方法进行网络重构后，网损约降低1/3，电压质量得到明显提升，最低节点电压可以提高到0.93 pu 以上，提高了2%左右，电压分布更加均匀，改善了网络电压水平，这表明文中提出的重构算法可以显著提升配电网系统运行的经济性和安全性。另外，文中的方法与单一目标函数重构方法相比，开关操作次数显著降低，对网损、电压质量等其他指标影响甚微，因而文中选取的综合目标函数更有现实意义。

5.3 动态重构结果分析

为验证文中方法在配电网故障时的动态重构效果，分别设置线路故障（支路25 断开）与节点故障（节点12 及其相连支路断开），对两种故障进行了动态恢复重构，结果如表3 所示。

表3 动态重构结果Table 3 Dynamic reconfiguration results

由表3 可知，因故障导致配电网网架结构变化时，应用该算法可以迅速完成网络动态恢复重构，实现非故障区域的快速复电，保障非故障区域的节点电压质量符合要求，网络损耗较低。因此，该算法应用于配电网故障动态恢复重构时，满足快速性、供电可靠性与经济性要求。

5.4 考虑DG接入的重构结果分析

在考虑分布式电源接入的情况下，仿真算例中接入了4 台分布式电源DG1—DG4，额定容量分别为60 kW、80 kW、120 kW、200 kW，功率因数分别为0.85、0.9、0.9、0.8，分别接入节点5、9、26、31。

采用多目标函数重构方法，仿真算例中权重系数的设置仍为a=0.353 0、b=0.254 7、c=0.221 3、d=0.171 0，对接入DG 的配电网进行重构，结果如表4 所示。

表4 考虑DG接入的重构结果Table 4 Reconfiguration results conidering DG access

由表4 可知，接入分布式电源后，节点电压质量有所提高，采用文中的方法重构后，网损降低了28.84%，节点最低电压提高了3.10%，结果证明了该方法对降低网损与提高节点电压质量作用明显。

5.5 不同算法结果对比

在5.4 节仿真条件的基础上，对比了文中提出的算法与常用的粒子群算法、蚁群算法和模拟退火算法的重构结果，如表5 所示。

表5 不同算法结果Table 5 Different algorithm results

由表5 可知，文中算法相比于其他三种算法在目标函数优化重构结果上性能更优，且重构时间最短，具有一定的对比优势。

6 结束语

建立考虑分布式电源接入的配电网多目标优化重构模型，选取了降低网损、均衡负载、提高电压质量、减少开关操作次数为目标函数，使得重构算法更具有实用性与推广价值。为更科学地确定目标函数各部分的权重系数，引入了层次分析法，通过确定目标层、准则层与方案层，构建层次结构模型。搭建了配电网优化重构决策支持系统架构，满足了数据采集、参数设置与结果输出的需求。采用改进遗传算法进行优化，实现了配电网的静态优化重构与动态故障恢复重构。通过仿真算例证明，文中算法可以正确、高效地实现含分布式电源接入的配电网的多目标优化，对实际配电网重构有一定的参考意义。