基于广义S变换和二维卷积神经网络的油纸绝缘局部放电超声信号识别

2023-11-29朱庆东朱孟兆王学磊顾朝亮高志新

山东电力技术 2023年11期

朱庆东，朱孟兆，王学磊，顾朝亮，高志新

（国网山东省电力公司电力科学研究院，山东济南 250003）

0 引言

电力变压器是电力系统中的核心设备，其安全运行对于维护电网安全有着重要意义。油纸绝缘作为油浸式变压器中的主要绝缘形式，其绝缘性能的劣化是造成变压器故障的主要原因［1-2］。局部放电作为内部绝缘故障的重要征兆，对其类型进行有效辨识可以为变压器状态的诊断评估提供参考［3-4］。

超声法是通过测量局部放电产生的超声信号进行局部放电检测的方法，具有传感器安装方便、抗电磁干扰能力强等优点，在变压器局部放电检测上得到了广泛的应用［5-6］。目前，针对超声信号的分析主要围绕在利用其时间信息对局部放电进行定位上［7-8］，但同时超声信号中也包含着大量的放电信息，能够有效提取超声信号中的关键信息，对局部放电类型进行识别，可以有效提高局部放电的检测效率。目前，局部放电信号的特征提取主要是从时域、频域和时频域等方面进行。文献［9］基于超声信号的时域、频域特征和时域压缩波形数据等特征提取方法，采用人工神经网络进行模式识别，获得了较好的效果。文献［10］运用小波包变换对局部放电超声信号进行分解，以小波包分解系数的统计量作为特征参量进行识别，但小波变换的效果依赖于小波基的选取，泛用性不强。文献［11］提出一种基于集合模态分解能量矩的特征提取方法，但是模态分解的分解级数通常是未知的，难以实际应用。

近些年，由于计算机技术的快速发展，深度学习方法在图像识别、语音识别、文本处理等方向取得了巨大的进步［12］。其中，卷积神经网络因其能够对样本中的特征进行自动提取，避免复杂的特征工程，在放电识别和故障诊断领域得到广泛的应用。文献［13］使用深度残差网络对局部放电信号的边际谱图像进行直接识别，获得更高的正确率和更优的泛化性能。文献［14］首先采用盲源分离对原始超声波信号进行处理，然后选用卷积神经网络进行训练，提高局部放电类型识别的准确性。

基于上述情况，提出一种基于广义S 变换（generalized S-transform，GST）和二维卷积神经网络（2-dimension convolutional neural network，2D-CNN）相结合的局部放电超声信号识别方法。GST 是一种高效的自适应时频分析方法，适合用于非平稳信号的处理上。基于GST 对超声数据进行处理，获得不同放电类型样本的时频特征图像，构建2D-CNN，自主提取时频图中的特征信息，实现局部放电超声信号的智能识别，并通过与其他方法进行对比，验证所提方法的准确性和有效性。

1 局部放电试验

1.1 试验平台

为采集油纸绝缘局部放电的超声信号，搭建局部放电试验平台，如图1 所示，主要包括高压测试回路、试验罐体和信号测量系统3 个部分。高压测试回路由调压器、100 kV/20 MVA 试验变压器、保护电阻和变比为2 000∶1 的阻容式分压器组成。试验罐体整体由有机玻璃制成，内部设有可更换电极，可以模拟不同类型下的局部放电。信号测量系统主要包括高频电流传感器（high frequency current transformer，HFCT）、超声传感器以及对应的采集装置。高频电流信号和超声信号通过同轴屏蔽电缆连接到采集卡上，最后由上位机进行数据处理。其中，超声传感器采用压电式声发射传感器，其谐振频率为75 kHz，可测量频率范围为15～150 kHz，后接信号放大装置，其滤波范围设置为20～120 kHz，该频段在变压器放电测量中具有一定的代表性［2］。

图1 局部放电试验平台Fig.1 Experiment platform of partial discharge

1.2 试验方法

为模拟变压器内部不同类型的局部放电情况，设计针板放电模型、柱板放电模型和球板放电模型，3 种缺陷模型的电极均为黄铜制作，绝缘纸板的厚度为1 mm，下电极均为半径75 mm、厚度为15 mm 的圆板电极，上电极分别为针状电极、柱状电极和球状电极。在进行试验前，对油纸样品进行预处理，使其水分含量满足标准［15］。

在正式试验前需要进行预试验，确定每种放电类型的局部放电起始电压（partial discharge inception voltage，PDIV）和击穿电压（breakdown voltage，BDV），然后在PDIV 和BDV 之间、不同电压等级下均进行数据采集，获得不同放电剧烈程度下的超声数据，采样频率为2.5 MHz。此外，为考虑传感器布设位置对信号的影响，对于每种放电类型，采集传感器在不同位置上获得的数据。对于采集到的超声信号，对其进行数据裁剪，以每一个工频周期（20 ms）内的超声信号为一组数据，进行后续的处理。

2 基本原理

2.1 广义S变换

S 变换是由Stockwell 等人［16］提出的一种时频分析方法，同时具有小波变换和短时傅里叶变换的优点。S 变换通过引入高斯窗函数，在保持相位信息的同时，使其具有可变的时频分辨率，在低频部分具有较高的频率分辨率，在高频部分具有较高的时间分辨率。进一步地，GST 通过给定调节因子，控制高斯窗函数宽度的变化，能够获得更好的时频分辨率，适用于非平稳信号的分析［17-18］。

对于任意一个平方可积的信号x（t），其GST 为

式中：f为频率；τ 为高斯窗函数的时移参数；λ为调节因子，当λ=1 时即为S 变换。

实际使用时，需要用到其离散形式，对于一个长度为N的离散时间序列x［a］，令a=jT（j=0，1，2，…，N-1），f=n/（NT），则其对应的离散GST 为

式中：T为其采样周期；X［f］为序列x［a］的离散傅里叶变换；m为累加符号的计数单位；n为离散频率值的序号数。

通过GST 可以将一个一维的时间序列变换到二维的时频域中，其横坐标为时间，纵坐标为频率，可以反映信号在对应时刻和频率的能量分布细节。

2.2 二维卷积神经网络

卷积神经网络（convolutional neural network，CNN）是深度学习最典型的算法之一，其通过引入卷积和池化运算，增强对局部相关性特征的提取能力，能够自主地对输入信号进行特征提取。卷积神经网络主要由卷积层、池化层和全连接层组成，输入经过多个卷积层和池化层自主提取特征，然后通过全连接层进行分类［19-20］。

卷积层是CNN 的核心，对输入和卷积核进行卷积运算，然后添加偏置并通过激活函数生成特征图。在训练过程中，卷积核的参数不断更新，可以强化卷积核的特征提取能力，对特征进行自主学习。对于2D-CNN，采用二维卷积核对二维输入图像中的二维分布特征进行提取。

池化层通过池化操作对卷积层获得的特征图进行降采样，一方面减少了计算的参数，一方面增强了网络的泛化性能。全连接层对经卷积层和池化层提取的特征图进行展开，最后结合分类器进行分类。

2.3 GST 与2D-CNN 相结合的局部放电超声信号识别方法

提出一种GST 与2D-CNN 相结合的局部放电超声信号识别方法，通过GST 构建超声信号的时频表达图谱，并使用2D-CNN 对图谱信息进行提取，进而对局部放电类型进行识别。该方法流程如图2所示。

图2 方法流程Fig.2 The method flowchart

具体步骤如下：

1）对获得的超声数据进行周期划分并筛选出有效数据，以一个工频周期内的数据为一组数据；

2）对信号进行GST，获得其时频图像，并将其进行灰度化处理，对数据进行归一化，增强模型的泛化能力；

3）生成局部放电超声信号时频图像样本集，并按比例划分为训练集和测试集；

4）构建卷积神经网络模型，并在训练集上进行模型训练，训练过程中不断调整网络模型以得到最优网络模型；

5）模型进行训练后，在测试集上对模型进行测试，获得模型对于各种局部放电类型的识别效果。

3 效果和分析

3.1 信号处理

对采集到的超声信号进行周期划分后得到针板放电数据2 270 条，柱板放电数据1 855 条，球板放电数据1 530 条，对其进行幅值筛选，最终得到有效数据共1 208 条，以7∶3 的比例划分训练集和测试集，各个放电类型的数据分布如表1 所示。

表1 有效数据样本分布Table 1 Distribution of valid data samples 单位：条

为减少数据量和处理时间，在进行GST 前，对信号进行降采样，将信号采样率降至500 kHz，则每组数据的长度为10 000。GST 的调节因子λ可以对时频图像的时频分辨率进行调整，本文选取λ=0.4，以获得最优的时频分辨率。在进行GST 时，仅对20～120 kHz 进行分析，得到不同放电类型的局部放电超声信号的变换结果如图3 所示。

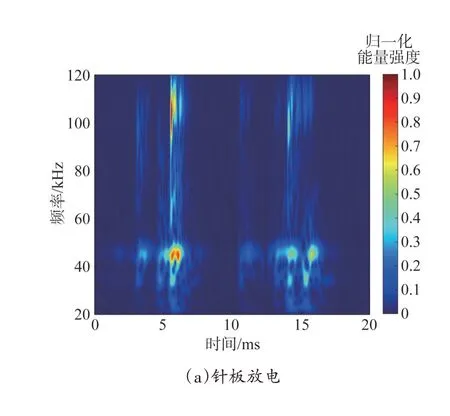
图3 不同放电类型超声信号的时频分布Fig.3 Time frequency distribution of ultrasound signals with different discharge types

由图3 可以看出，不同放电类型经GST 后的时频分布存在明显区别，时频图像中包含着丰富的细节信息，后续通过卷积神经网络可以有效地提取关键特征并进行放电类型的识别。

3.2 模型结构与参数设置

网络模型结构如表2 所示。

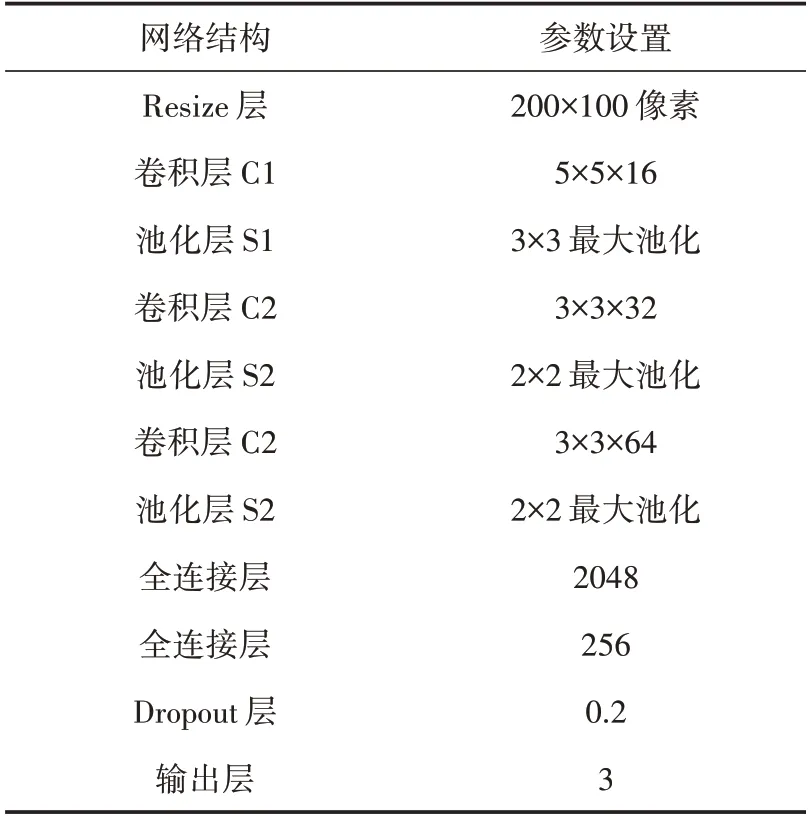
表2 模型结构参数Table 2 Parameters of model structure

首先将输入尺寸压缩到200×100 像素，以减少后续的计算量。然后输入连续通过3 个卷积池化单元，首先通过大小为5×5 的卷积核提取初级特征，然后通过两组大小为3×3 的卷积核进一步提取深层特征。在经过卷积池化后，特征图的尺寸不断降低，通道数目不断增加，最后通过两层全连接层将其展开成一维向量，并通过softmax 函数进行分类。为减小过拟合，在全连接层之后加入dropout 层，丢弃概率设置为0.2。

除以上超参数，对损失函数、学习率和优化算法进行多次测试，最终选用损失函数为交叉熵函数，学习率设置为0.01，优化算法为小批量随机梯度下降算法。

3.3 识别效果分析

本文算法的实现依靠python 实现，深度学习框架为pytorch，验证本文方法的平台为RTX 3090 显卡。训练过程中损失和准确率随迭代次数的收敛曲线如图4 所示，可以看出，随迭代次数的增加，模型的损失值不断减小，识别准确率不断上升。在50次迭代后模型已经趋于稳定，可以达到较好的效果，在经过200 次迭代后，模型基本收敛，损失值降低到0.04 左右，在训练集上的准确率达到98%左右。

图4 训练过程中损失和准确率的变化曲线Fig.4 The variations of loss and accuracy during training

为进一步说明模型在测试集上的表现，列出测试集上识别结果的混淆矩阵，如表3 所示。

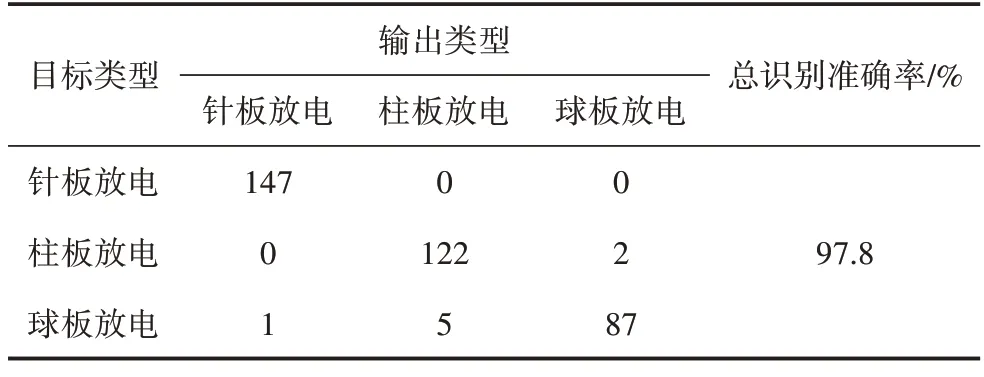
表3 识别结果的混淆矩阵Table 3 Confusion matrix of recognition results

由表3 可以看出，测试集整体的识别准确率可以达到97.8%，其中对于针板放电的样本全部识别正确，对于柱板放电有2 个样本被错误识别为球板放电，球板放电的识别准确率较低，有1 个样本被识别为针板放电，5 个样本被识别为球板柱板放电。可以看出，本文方法对于局部放电类型识别整体上具有较高的准确率，能够有效区分几种相似的缺陷类型。

3.4 与其他方法对比

将本文方法与其他3 种方法进行对比，以验证其在局部放电超声信号识别上的优势。用于对比的方法所采用的训练集和测试集与本文方法一致，以总体识别准确率为指标评价不同方法的效果，识别准确率为识别准确的样本数和总样本数的比值，各方法的识别效果如表4 所示。

表4 不同方法的识别效果对比Table 4 Comparison of recognition effects among various methods 单位：%

方法1：对超声信号进行小波包变换，提取能量最大的节点的统计量作为特征参量［7］，然后采用支持向量机进行识别。

方法2：对超声信号进行GST，对获得的时频图像进行特征降维，然后采用BP 神经网络进行分类识别。

方法3：特征图像生成方法选用短时傅里叶变换，采用CNN 进行图像识别［11］。

从表4 中可以看出，本文方法比其他方法具有更高的识别准确率，能更有效地利用超声信号的内在信息对放电进行识别。方法1 和方法2 分别基于小波包变换和GST 对超声信号进行处理，然后用分类器对提取的特征量进行分类识别，在特征提取步骤会丢失大量的有效信息，造成识别准确率不高，显著低于深度学习方法。方法3 采用短时傅里叶变换进行特征图的生成，采用卷积神经网络进行特征提取，能够达到94.8%的准确率。本文方法采用GST进行时频变换，具有更高的时频分辨率，可以使故障特征在时频域中更加突出，识别准确率更高。