乡镇生活污水溶解氧浓度模糊神经网络PID 控制系统研究

陈远龙 李致樯 甘鑫平

（合肥工业大学机械工程学院，安徽合肥 230009）

1 引言

厌氧—缺氧—好氧活性污泥法（AAO）工艺是目前比较成熟的污水处理工艺，其针对乡镇生活污水中氮磷含量高等特点［1］，具有较好的处理效果。根据污水处理工艺，好氧池中溶解氧浓度对污水的处理效果起着至关重要的作用［2］。溶解氧浓度过高，污泥中的微生物过度生长，污水中的污染物分解速度过快，活性污泥发生丝状膨胀，导致活性污泥的活性降低，污水处理的效果较差，并且增加能量损耗；溶解氧浓度过低，好氧池由于缺氧发生污泥腐化，污水中的污染物将难以处理干净，出水水质达不到处理要求［3］。因此，应精确控制好氧池中溶解氧的浓度，使出水水质达到排放标准。

针对溶解氧浓度控制的问题，国内外学者进行了大量研究。G Bertanza L 等［4］对采用活性污泥法的污水处理厂中的曝气系统采用模糊控制策略，相比于传统的PID 控制策略，出水水质可提高7%～8%，曝气能耗减少12%。Do Trung Hai 等［5］采用模糊控制结合遗传算法来控制污水中的溶解氧浓度，并与经典的PID 控制器进行了比较，结果表明，前者控制效果更好，系统的运行成本更低。许进超等［6］提出了把自组织模糊神经网络应用在污水处理的溶解氧控制中，并采用梯度下降算法对神经网络进行优化，在BSM1 上进行仿真验证，结果表明，采用自组织模糊神经网络对溶解氧浓度具有较好的预测和控制效果。权利敏等［7］针对污水处理中溶解氧浓度存在不确定性强、干扰多和难以精确控制的问题，提出了采用熵模糊神经网络控制策略的溶解氧浓度控制方案，并在BSM1 平台上进行仿真验证，结果表明，采用熵模糊神经网络可以精确控制溶解氧浓度。

本文设计了一个5 层的模糊神经网络PID 控制器，将神经网络和模糊PID 控制相结合。采用的神经网络为径向基函数（Radial Basis Function，RBF）神经网络，具有训练时间短、学习速度快以及无局部极小等优点，适合在线实时控制。通过RBF 神经网络来实现模糊逻辑，利用RBF 神经网络的自学习能力在线优化调整控制规则，自适应能力强。采用此模糊神经网络PID 控制器，可以更好地控制好氧池中溶解氧的浓度变化。

2 溶解氧浓度控制原理和数学模型

2.1 溶解氧浓度控制原理

因为好氧池中的微生物要进行好氧反应，所以需要用鼓风机向好氧池中传输氧气，鼓风机的转速决定了好氧池中溶解氧浓度的高低。为了节省能耗和调节方便，本研究设计选用变频器来控制鼓风机的转速，实现调节好氧池中溶解氧浓度的目的。好氧池中溶解氧控制原理如图1 所示。

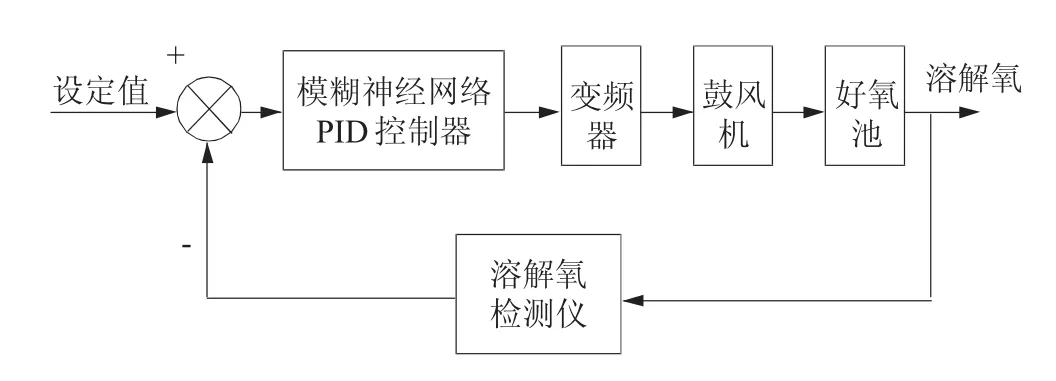
图1 好氧池溶解氧控制原理

2.2 溶解氧浓度控制数学模型

溶解氧浓度控制的数学模型的重点在于好氧池中溶解氧浓度变化和变频风机运转机理。

2.2.1 好氧池中溶解氧浓度数学模型建立

溶解氧浓度的物料平衡算式为：溶解氧浓度变化率＝溶解氧输入率-溶解氧输出率+氧化生成率-溶解氧消耗率，根据该算式可以建立如下的活性污泥动态模型：

式中，Q 为空气流量；V 为反应池容积；y（t）为溶解氧浓度；yin（t）为鼓入空气的溶解浓度；yout（t）为输出溶解浓度；ysat（t）为饱和溶解氧浓度；KLa［u（t）］为氧气转换函数；K 为溶解氧反应速率常数。

KLa［u（t）］的大小与空气流量的变化呈非线性关系，可用常数Kmax表示，因此式（1）可变换为：

对式（2）作拉普拉斯（Laplace）变换得：

对式（3）简化可得：

另外，溶解氧的检测是非线性的，具有一定滞后性。将因检测造成的滞后用τ 来表示，则修正后的模型为：

式（5）可近似认为是溶解氧浓度的数学模型，根据实际经验和测量［8］可以得出仿真模型中的U＝17，K1＝0.016，τ1＝20。

2.2.2 变频风机控制数学模型

鼓风机通过变频调速控制，根据鼓风机电机转速、鼓风机空气流量和电源频率三者之间的关系，以及空气由风机进入好氧池中需要一定时间，则变频风机控制的数学模型通常可近似表示为：

根据实际经验和测量［9］可以得出仿真模型中的T＝0.6，K2＝0.8，τ2＝5。

因此由式（5）和（6）可知，溶解氧浓度控制的数学模型为：

3 模糊神经网络PID 控制器设计

采用标准模型设计的模糊神经网络结构如图2所示，共5 层结构，其中将溶解氧检测仪测得的实际溶解氧浓度值与设定值的偏差e 和偏差的变化率ec，作为模糊神经网络控制器的输入变量；为了实现对PID 控制3 个参数的自适应整定，模糊神经网络控制器的输出为PID 控制的3 个参数的增量Kp，Ki和Kd。

图2 基于标准模型的模糊神经网络结构

第一层为输入层，主要作用是将输入值传入到下一层，其输入输出分别如下：

输入：Ii1＝xi

输出：Oij1＝Iij1＝xi

式中，i=1，2，…，n，n 为输入变量；j＝1，2，…，mi，mi是x 的模糊分割数。

本研究设计的输入层有两个节点，分别与输入变量溶解氧浓度偏差e 和偏差变化率ec 相连。

第二层为模糊化层，主要作用是计算各输入分量属于各语言变量值模糊集合的隶属度函数μij。本研究设计采用的隶属度函数为高斯函数，其输入输出分别如下：

输入：Iij2=Oij1

式中，cij和σij分别表示隶属度函数中心和宽度。

第三层为模糊推理层，主要作用是用来匹配模糊规则的前件，计算出每条模糊规则的适用度，其输入输出分别如下：

输入：Il3=Oij2

式中，kn∈{1，2，…，mn}，l＝1，2，…，m。

第四层为清晰化层，主要作用是实现模糊神经网络清晰量的输出。本研究设计采用重心法进行清晰化，其输入输出分别如下：

输入：Il4=Oj3

第五层为输出层，主要作用是得出经过模糊神经网络计算后的输出，即最终输出结果Kp，Ki 和Kd，其输入输出分别如下：

输入：Il5=Ol4

本研究设计采用Simulink 工具箱中的系统函数（System Function）对溶解氧浓度控制系统的模型进行搭建。根据上述公式，创建S-Function 源代码，一般可以通过M 文件、C 文件或MEX 文件编写系统函数，本研究设计选用M 文件编写S-Function，其中模块采用率为1。

4 仿真系统搭建

将创建完成的S-Function 模块导入溶解氧浓度的仿真模型中，同时创建基于模糊PID 控制和PID控制的溶解氧浓度的仿真模型作为对比，仿真模型如图3 所示。

图3 模糊神经网络、模糊PID 和PID 的Simulink 仿真结构

模糊神经网络PID 的内部结构如图4 所示。

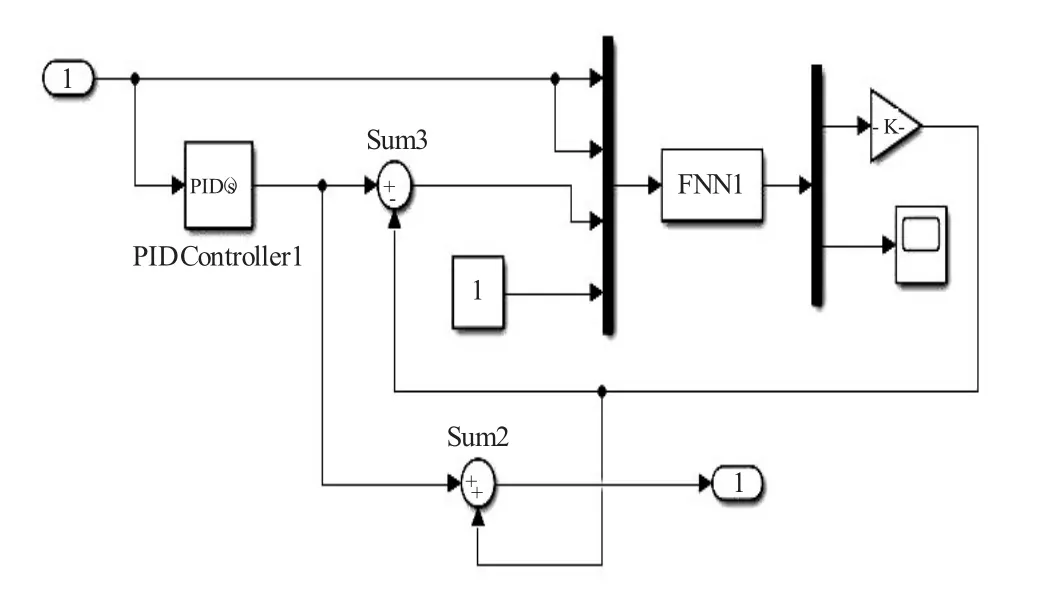
图4 模糊神经网络PID 内部结构

5 仿真结果

通过Simulink 进行仿真，输入值为2 的阶跃信号，仿真结果如图5 所示。

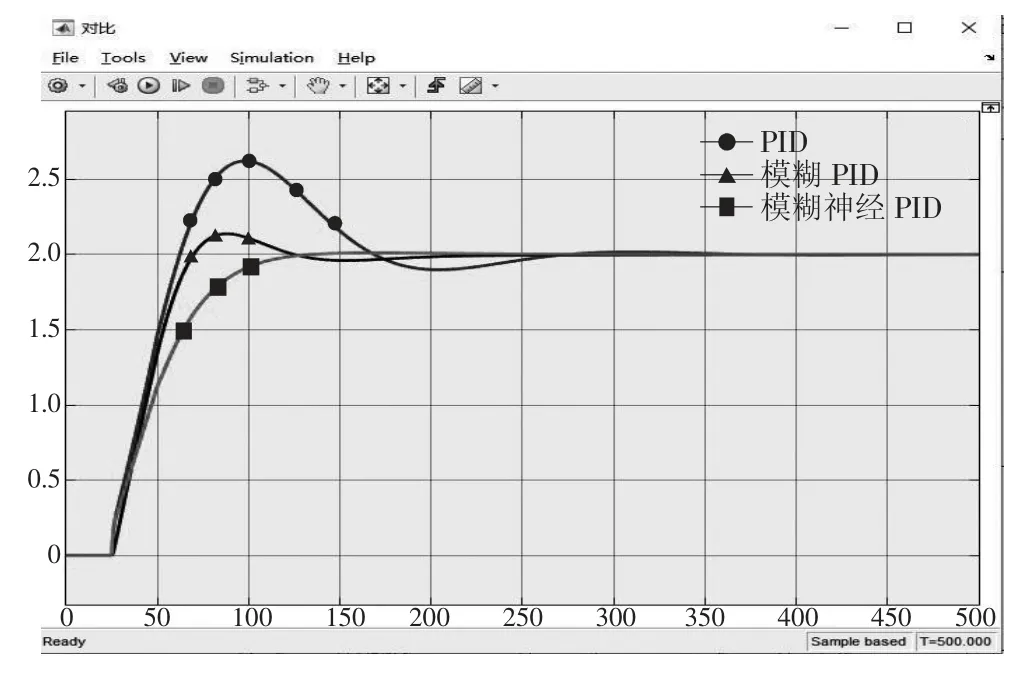
图5 各控制方案的仿真图

各种控制方案的性能指标见表1。

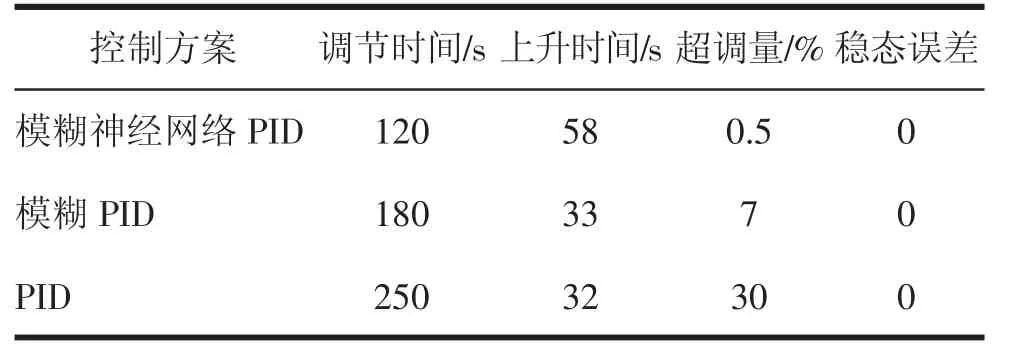
表1 各种控制方案的性能指标

仿真结果表明，具有自学习能力的模糊神经网络PID 控制可以对好氧池中的溶解氧浓度进行快速有效的控制，并且模糊神经网络PID 控制的快速性和超调量相比于模糊PID 以及传统PID 都更小。

由于溶解氧浓度控制易受其他因素干扰，因此当控制系统稳定之后，在t＝400 s 处给系统一个值为1 的阶跃干扰，仿真结果如图6所示。

图6 阶跃干扰下各控制方案的仿真图

阶跃干扰下各种控制方案的性能指标见表2。

表2 阶跃干扰下各种控制方案的性能指标

仿真结果表明，模糊神经网络PID 的鲁棒性更强，具有更好的抗干扰能力。

在实际的溶解氧控制过程中，被控对象受多种因素影响，使得溶解氧控制模型是实时变化的。所以要求控制系统即使在模型变化的情况下，依然有较好的控制效果。因此，将模型的开环增益扩大50%，对此控制系统进行仿真，仿真结果如图7 所示。

图7 模型失配下各控制方案的仿真图

模型失配下各种控制方案的性能指标见表3。

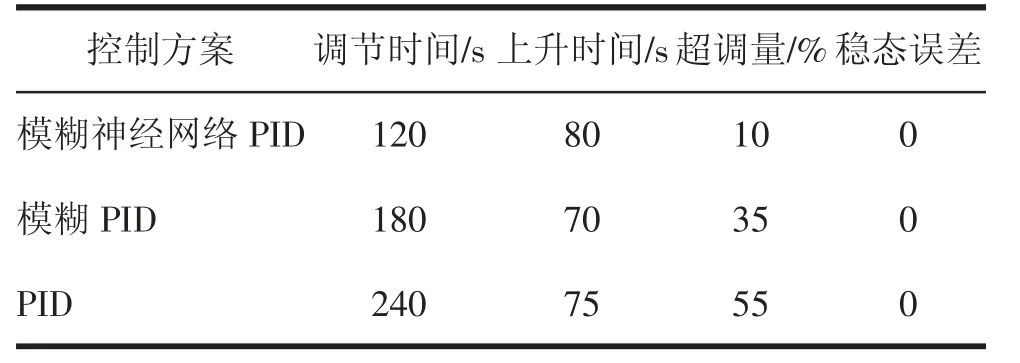
表3 模型失配下各种控制方案的性能指标

仿真结果表明，模糊神经网络PID 具有更好的容错性。

6 结论

本研究针对乡镇生活污水处理中溶解氧浓度控制问题，设计了一种模糊神经网络PID 控制方案，并在MATLAB 中对模糊神经网络PID、模糊PID 和PID 这3 种控制方案进行仿真模拟。仿真结果表明，在不加阶跃干扰、加阶跃干扰和模型失配3 种情况下，模糊神经网络PID 控制的响应速度和超调量相比于模糊PID 和PID 控制都更小，鲁棒性强并且提高了控制系统的抗干扰能力，控制效果更好，具有更高的实用价值。