基于改进关联分析的行业短期电力负荷预测

2023-11-28虞殷树陈东海白文博

浙江电力 2023年11期

虞殷树，陈东海，朱耿，贺旭，白文博

（1. 国网浙江省电力有限公司宁波供电公司，浙江宁波 315000；2. 宁波市电力设计院有限公司，浙江宁波 315000）

0 引言

短期电力负荷预测是调度计划安排的重要依据，对于电力系统的安全经济运行具有重要意义［1-3］。在进行地区电网的短期负荷预测时，由于各个行业的负荷特性差异较大，需利用配电网台账信息按所属行业对负荷进行分解和预测，以提高负荷预测的精细化程度。随着各行业历史负荷数据、气象数据等多元数据的积累，利用大数据、机器学习技术对各行业的负荷特性和影响因素进行分析，有助于提高对不同行业负荷的预测准确性，进而提升短期电力负荷预测的效果［4-6］。

目前，针对短期电力负荷预测已有不少研究。文献［7］通过集合经验模态分解将电力负荷分解为低频和高频分量，再分别使用线性回归和神经网络方法对低频和高频分量进行预测；文献［8］采用LSTM（长短期记忆）网络和XGBoost（极端梯度增强）模型分别进行负荷预测后，使用误差倒数法对两者的预测结果进行组合，得到最终的预测结果；文献［9］对用户负荷数据进行聚类处理，得到不同负荷特性的用户群，并针对不同用户群进行负荷预测模型构建，最终将各个用户群的预测负荷整合为全局预测结果；文献［10］采用卷积神经网络和循环神经网络对历史负荷序列的规律进行特征学习和提取，并引入注意力机制提升短期负荷预测的精度。上述研究仅利用历史负荷数据进行短期负荷预测，而行业负荷不仅与历史负荷数据有内在的相关性，也受到气象、日类型等外部因素的显著影响，需要对外部影响因素加以考虑，以提升负荷预测的准确性。

为此，一些研究在进行短期负荷预测时考虑了外部影响因素与负荷的关联性。文献［11-12］采用Pearson相关系数分析电力负荷与外部影响因素的相关性，为负荷相似日的选择提供依据，但Pearson 相关系数只适用于线性相关性的分析，无法捕捉到电力负荷与外部影响因素的非线性相关性；文献［13-14］采用Copula函数衡量电力负荷与外部影响因素之间的非线性相关性，但是Copula函数的具体形式需要人为确定，关联分析的准确性容易受到主观因素的影响，同时上述研究的关联性分析结果只用于选取一部分与负荷关联性强的外部影响因素，无法全面地量化各个因素对电力负荷的影响；文献［15-18］采用机器学习方法对电力负荷与外部影响因素之间的关联性进行自动提取，但机器学习方法的可解释性较差，且在没有足够大的数据量时容易受到变量随机波动的影响而陷入过拟合。

针对上述问题，本文提出一种基于关联分析和卷积神经网络的行业短期电力负荷预测模型。通过优化k-means 聚类算法和引入标准互信息指标，改进了外部影响因素与负荷关联性的计算方法，并基于卷积神经网络设计一种计及外部影响因素关联性的负荷预测网络，提升了地区电网各行业短期电力负荷预测的准确性。

1 行业短期电力负荷预测模型

基于关联分析和卷积神经网络的行业短期电力负荷预测模型整体结构如图1所示。将历史负荷数据、外部影响因素数据、行业负荷数据都划分为训练集和测试集，在训练阶段使用训练集的数据进行关联性结果的计算和负荷预测网络的训练，在测试阶段则利用训练后的负荷预测网络进行行业负荷预测。

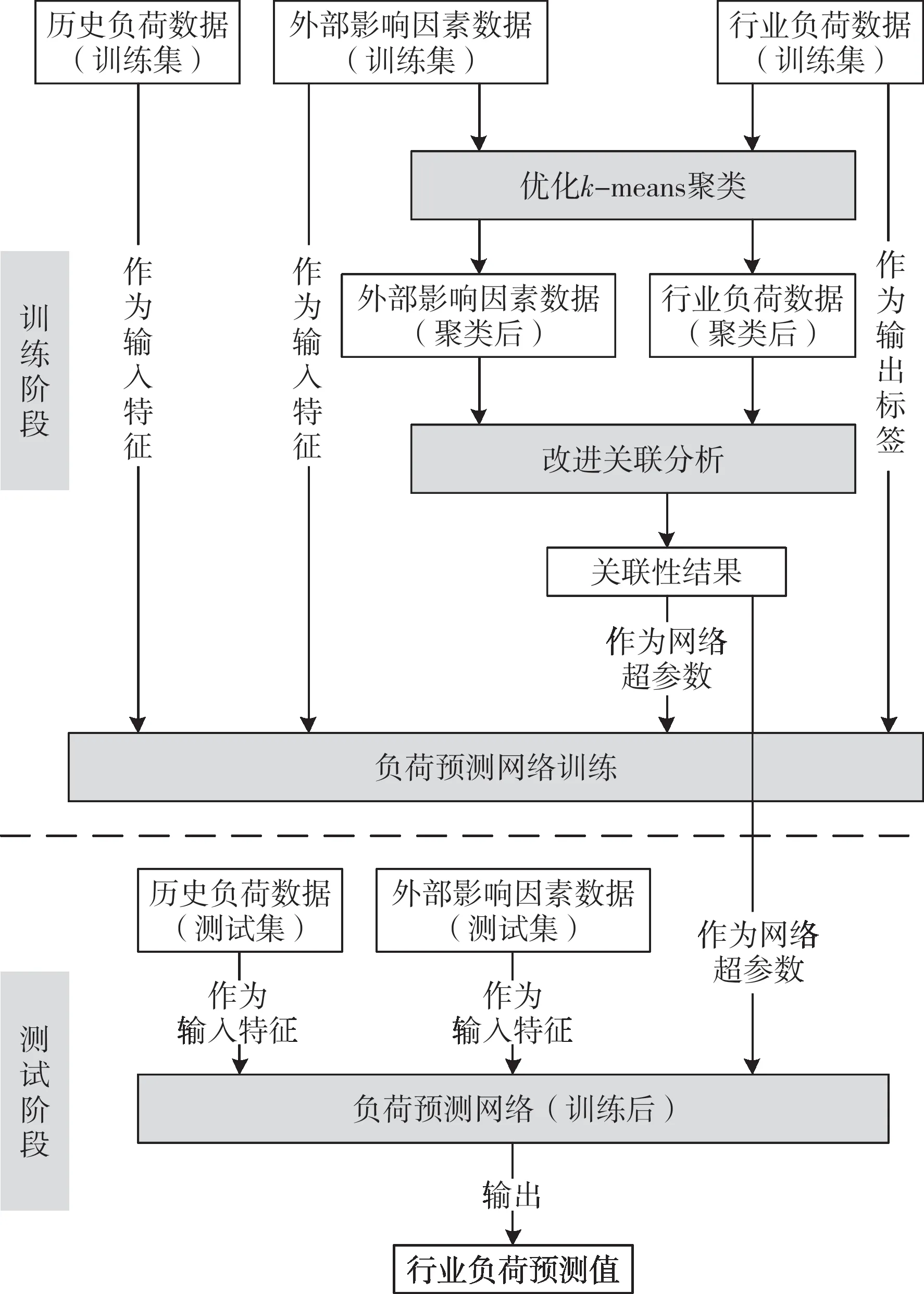
图1 行业短期电力负荷预测模型整体结构Fig.1 Overall structure of the short-term power load forecasting model for industrial sectors

训练阶段主要分为优化k-means 聚类、改进关联分析和负荷预测网络训练3 个步骤，具体如下：

1）对k-means 聚类算法进行优化，并采用优化后的k-means 聚类算法对外部影响因素数据和行业负荷数据进行聚类处理，以改善后续关联分析的准确性。

2）对关联分析方法进行改进，以标准互信息为关联性指标，并采用聚类后的数据代替原始数据进行标准互信息计算，定量分析各种外部影响因素与行业负荷的关联性。

3）设计一种计及外部影响因素关联性的负荷预测网络，将关联性结果作为网络的超参数，并以训练集的历史负荷数据和外部影响因素数据为输入特征、行业负荷数据为输出标签，对负荷预测网络进行训练。

在测试阶段，将测试集的历史负荷数据和外部影响因素数据作为输入特征，输入训练后的负荷预测网络，即可输出相应的行业负荷预测值。

2 外部影响因素与行业负荷数据聚类处理

在分析外部影响因素与行业负荷之间的关联性前，需要对数据进行聚类处理，以提高关联分析的准确性。对于无监督的聚类问题，目前较为常用的是k-means 聚类方法［19］，但k-means 聚类方法需要人为指定聚类的簇数k，适应性不够且主观性较强，聚类效果容易受到数据数量和分布情况的影响。为此，本文对k-means 聚类算法进行优化，采用平均轮廓系数进行最佳k值的确定，避免聚类算法对于人工经验的依赖，提高算法的适应性。优化后的k-means聚类算法步骤如下：

1）输入待聚类数据（例如温度数据）在一个时间段内所有的C个采样值x（c）（c∈｛1，2，…，C｝），并设定k值的上限kmax为10。

2）令k=2。

3）采用k-means 聚类算法对所有采样值进行一维聚类，聚类时以采样值和聚类中心数值之差的绝对值作为划分聚类簇的标准，聚类后生成k个簇。

4）聚类完成后，计算每个采样值x（c）的轮廓系数l（c）。若采样值x（c）为孤立点，即x（c）所在簇内只有x（c）一个采样值，则其轮廓系数l（c）为0；否则，按照式（1）至（4）计算x（c）的轮廓系数l（c）：

式中：x（j）为x（c）所在簇内的其他采样值；x（q）为x（c）所在簇外第p个簇内的采样值；l1（c）为簇内凝聚度；l2（p，c）为x（c）所在簇与其他第p个簇的簇间分离度；l3（c）为所有簇间分离度的最小值；n1（c）为x（c）所在簇内的采样值数目；n2（p，c）为除x（c）所在簇外第p个簇内的采样值数目。

5）计算出每个采样值x（c）对应的轮廓系数l（c）后，求出此时的k值对应的平均轮廓系数：

6）令k自加1，若k>kmax，则继续执行步骤7），否则返回步骤3）。

7）取所有的平均轮廓系数l0（k）（k∈｛2，3，…，kmax｝）中的最大者所对应的k值，作为最佳的聚类簇数，记为k0，并将步骤3）中聚类簇数为k0时的聚类结果作为最终的聚类结果。

优化k-means聚类后共形成k0个簇，每个簇都有1个聚类中心，聚类中心的值为簇内所有采样值的平均值。

3 基于标准互信息的改进关联分析方法

行业负荷和外部影响因素之间的相关性往往是非线性的，例如温度因素对居民负荷的影响，在低温和高温时居民负荷都会升高，而温度适中时居民负荷较低。若采用Pearson系数、Spearman系数等常用的相关系数对相关性进行计算，由于正相关部分与负相关部分互相抵消，将得出负荷与温度相关性接近于0的结论，不符合实际情况。

为此，本文借鉴信息论中的互信息概念［20-21］，采用标准互信息对行业负荷与外部影响因素的关联性进行分析，以充分考虑两者的非线性相关性。对于待分析的行业负荷与外部影响因素，已知一个时间段内C个采样时刻的影响因素值x（c）和负荷值y（c）（c∈｛1，2，…，C｝），所有x（c）构成序列X，所有y（c）构成序列Y，其中x（c）共有M种可能取值（M≤C），记为x1（m）（m∈｛1，2，…，M｝），y（c）共有N种可能取值（N≤C），记为y1（n）（n∈｛1，2，…，N｝），影响因素与负荷的标准互信息值J（X；Y）计算方法如下：

其中：

式中：I（X；Y）表示X与Y的互信息值；H（X）和H（Y）分别为X和Y的信息熵；P（x1（m），y1（n））表示同时满足x（c）=x1（m）和y（c）=y1（n）的采样时刻占所有采样时刻的比例；P（x1（m））表示满足x（c）=x1（m）的采样时刻占所有采样时刻的比例；P（y1（n））表示满足y（c）=y1（n）的采样时刻占所有采样时刻的比例；J（X；Y）的取值范围为［0，1］，其值越大表明影响因素与负荷的关联性越强。

但是，直接采用原始数据X与Y的标准互信息会使关联性分析受到数值细微差异的影响，无法把握变量的主要变化趋势。以表1中的两组数据为例，每组数据均由4个采样时刻的温度值和负荷值构成，按照式（6）—（9）计算，第1 组数据的J（X；Y）为1（表明温度和负荷的关联性很强），而第2组数据的J（X；Y）为0（表明温度和负荷的关联性很弱），两组数据的关联性结果差别很大，但实际上两组数据仅仅存在小数点后的细微差别，表明其中一组数据的关联性结果不合理。

表1 温度与负荷采样数据示例Table 1 Temperature and load data samples

按照实际经验，在温度值x（c）出现较明显的变化（从约20 ℃变化到约30 ℃）时，如果负荷值y（c）的分布基本没有变化（50%概率约为1 000 MW，50%概率约为2 000 MW），则应当认为温度和负荷的关联性很弱，因此对于这两组数据而言，第2组数据J（X；Y）=0的结果更为合理。

为了避免由于数值细微差异导致关联性结果不合理的问题（如表1中第1组数据的情况），本文对关联分析方法进行改进，采用经过聚类处理后的数据替换原始数据，进行标准互信息的计算。记采样值x（c）所在簇的聚类中心值为u（c），所有u（c）构成序列U，采样值y（c）所在簇的聚类中心值为v（c），所有v（c）构成序列V。u（c）共有F种可能取值（F≤C），记为u1（f）（f∈｛1，2，…，F｝），v（c）共有G种可能取值（G≤C），记为v1（g）（g∈｛1，2，…，G｝），则影响因素与负荷经过聚类中心替换后标准互信息值J0（U；V）计算方法如下：

其中：

式中：I0（U；V）为u（c）与v（c）的互信息值；H0（U）和H0（V）分别为U和V的信息熵；P（u1（f），v1（g））为同时满足u（c）=u1（f）和v（c）=v1（g）的采样时刻占所有采样时刻的比例；P（u1（f））为满足u（c）=u1（f）的采样时刻占所有采样时刻的比例；P（v1（g））为满足v（c）=v1（g）的采样时刻占所有采样时刻的比例；J0（U；V）的取值范围为［0，1］，其值越大表明影响因素与负荷的关联性越强。

表1的两组原始数据经过聚类处理后如表2所示，表2的两组数据按照式（10）—（13）计算得到的J0（U；V）均为0，与实际经验相符，说明原始数据经过聚类处理后，求得的标准互信息能更准确合理地反映行业负荷与外部影响因素的关联性。

表2 聚类处理后温度与负荷采样数据示例Table 2 Temperature and load data samples after clustering

4 行业短期负荷预测网络

4.1 基于卷积神经网络的特征提取

卷积神经网络具有模型复杂度较低、易于并行计算的优势，且可通过多尺寸窗口同时提取多种时间跨度的信息，在负荷预测任务中被广泛采用［22-23］。本文采用卷积神经网络对原始数据进行特征提取，以挖掘原始数据中的关键信息，用于短期负荷预测。原始数据包括历史负荷数据，以及温度、相对湿度、风速、降水量、节假日等外部影响因素数据。

对于历史负荷数据，进行归一化后采用待预测时刻前t1个小时的采样值作为输入数据，构成一个t1维的输入向量，记为V，然后用多个h×1 维的卷积窗口对V进行卷积运算（h可有多种取值，对应不同的时间跨度）。假设用h×1维的卷积窗口W对V进行卷积运算，并进行最大值池化，得到特征值e：

式中：Va：a+h-1表示由输入向量V的第a至a+h-1维的值组成的向量；b为偏置项。

最后将多个卷积窗口得到的特征值进行拼接，得到历史负荷特征向量e0。

对于外部影响因素数据，进行归一化后采用待预测时刻前t2个小时的所有采样值以及从待预测时刻起t3个小时的所有预报值作为输入数据，构成（t2+t3）维的输入向量。然后，同样采用多个卷积窗口，对输入向量进行卷积运算。最终每个外部影响因素均生成一个特征向量，其中第r个外部影响因素（r∈｛1，2，…，R｝，R为外部影响因素个数）的特征向量为e1，r。

4.2 计及外部影响因素关联性的负荷预测网络

不同外部因素对行业负荷受的影响程度不尽相同，因此在进行各个行业的电力负荷预测时，应充分考虑行业负荷与各个外部影响因素的关联性强弱。为此，采用第3章基于标准互信息的改进关联分析得到的关联性结果，作为负荷预测网络的超参数，融合到负荷预测网络结构中，从而构建计及外部影响因素关联性的行业短期负荷预测网络，如图2所示。

图2 行业短期负荷预测网络Fig.2 Short-term load forecasting network for industries

首先，按照4.1节的方法，基于卷积神经网络对历史负荷和外部影响因素数据进行特征提取，得到历史负荷特征向量e0和外部影响因素特征向量e1，1到e1，R。

然后，在预测某一行业的电力负荷时，采用第3章基于标准互信息的改进关联分析方法得到的关联性结果，即行业负荷与各个外部影响因素之间的标准互信息值，作为权重超参数。具体做法为：将行业负荷与第r个外部影响因素（r∈｛1，2，…，R｝，R为外部影响因素个数）的标准互信息值记为J0，r，对标准互信息值进行归一化处理，得到行业负荷与第r个外部影响因素的归一化标准互信息值J1，r：

并以J1，r为第r个外部影响因素的特征向量e1，r的权重，将所有外部影响因素特征向量加权求和，得到融合向量e2：

最后，将历史负荷数据的特征向量e0和融合向量e2进行拼接，得到拼接向量e3：

再使用SVR（支持向量回归）模型对拼接向量e3进行预测，得到待预测时刻的负荷预测值。

5 算例分析

5.1 实验数据集

实验采用某地区电网公司2016—2020 年的电力负荷数据，该地区的电力用户按所属行业性质可分为工业、商业、公共事业和居民用户，通过配电变压器和用户的对应关系，统计用户所属行业及其用电负荷，可收集各个行业的负荷数据，同时采集温度、相对湿度、风速、降水量、是否节假日等外部影响因素数据进行实验，数据的采样间隔均为1 h，其中节假日因素由于只有1 或0两种取值，因此在关联分析前无需对其进行聚类处理。将2016—2019 年的数据作为训练集，用于计算各行业负荷与各种外部影响因素的关联性，并训练行业短期负荷预测网络；2020 年的数据作为测试集，用于测试本文所提方法的预测效果。

5.2 实验评价指标

为评估行业短期负荷和地区电网总负荷预测的精度，采用MAPE（平均绝对百分比误差）作为一个评价指标。同时，在评估负荷预测精度的基础上，采用RMSE（均方根误差）指标对预测结果围绕实际值的波动程度进行衡量，以评估负荷预测结果的稳定性。

设共有D个待预测时刻，每个时刻的负荷预测值为y（d）（d∈｛1，2，…，D｝），负荷实际值为y0（d），则MAPE指标计算方法为：

RMSE指标计算方法为：

5.3 实验模型与参数

实验对照模型的设置，主要从是否对k-means聚类算法进行优化、是否对关联分析方法进行改进、是否在负荷预测网络设计中计及外部影响因素关联性这3个方面进行考虑，对应地设置3个对照模型组A、B、C，如表3 所示。对照模型组A包括A1、A2、A3 3 个对照模型，采用不经过优化的原始k-means 聚类算法对原始数据进行聚类处理，并分别指定聚类簇数k为3、6、9；对照模型组B包括B1、B2、B3 3个对照模型，分别采用无聚类的标准互信息、Pearson 相关系数、t-Copula 相关系数进行关联分析；对照模型组C 包括C1、C2 2 个对照模型，其中C1 模型不计及外部影响因素的作用，在负荷预测网络中不生成融合向量e2，只通过历史负荷特征向量e0进行负荷预测，C2 模型不计及外部影响因素关联性的作用，在负荷预测网络中将所有代表关联性的权重超参数J1，r均设置为1/R，即对各个外部影响因素特征向量e1，r等权重求和。

表3 对照模型设置情况Table 3 Settings of controlled models

经过预实验的参数寻优，将历史负荷输入向量维数t1设置为72，外部影响因素输入向量相关参数t2和t3分别设置为72 和24，对每个输入向量均采用30 个3×1 维、30 个6×1 维和30 个12×1维的卷积窗口进行卷积运算。

5.4 实验结果与分析

实验采用基于标准互信息的改进关联分析方法对训练集各行业负荷与各种外部影响因素的关联性进行分析，得到每个行业的负荷与各种外部影响因素的归一化标准互信息，即关联性结果，如图3所示。

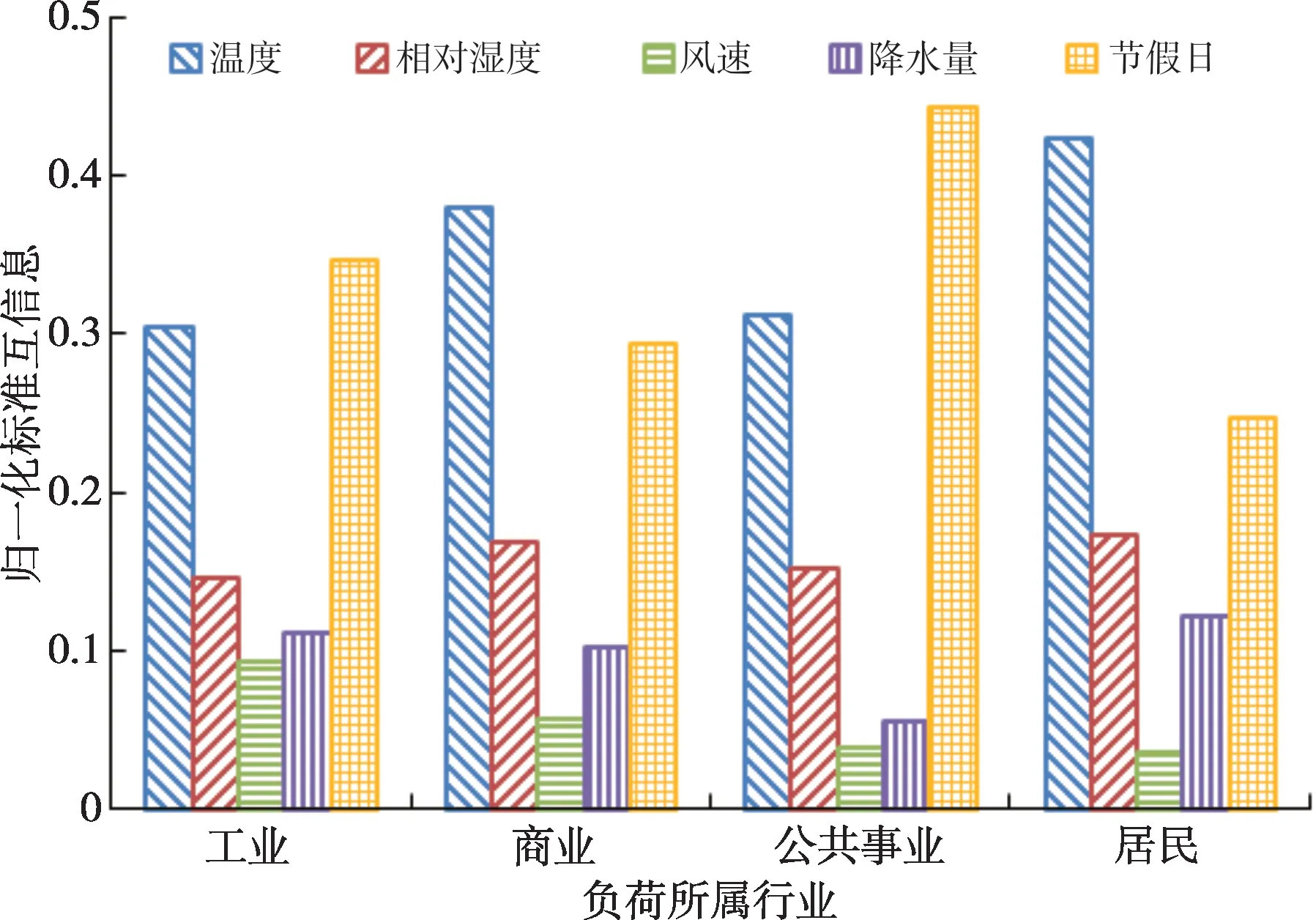
图3 行业负荷与外部影响因素关联性Fig.3 Correlation between industry load and external influencing factors

从图3可以看出，该地区对各行业负荷有较大影响的外部因素主要是温度和节假日，但不同行业的负荷与两者关联性的相对强弱也有所区别，工业和公共事业负荷与节假日因素的关联性更强，而商业和居民负荷与温度因素的关联性更强。除此之外，相对湿度对于各个行业负荷的影响比重较为均匀，而风速对于工业负荷的影响比重明显高于其他三类行业负荷，降水量对于公共事业负荷的影响比重则明显低于其他三类行业负荷。

结合上述关联性结果，采用基于关联分析和卷积神经网络的行业短期电力负荷预测模型对测试集各行业负荷进行预测，并将各行业负荷的预测值求和，得到地区电网总负荷的预测结果。同时，用表3中的对照模型进行同样的实验，并分别统计各个模型在测试集上的预测结果，得到相应的MAPE和RMSE指标如表4和表5所示。

表4 各行业负荷和总负荷预测MAPE值Table 4 The predicted MAPE values of industrial loads and total loads

从表4可以看出，本文模型在各个行业负荷和总负荷预测的MAPE 值均为最小，即对于各个行业负荷和总负荷的预测均有最高的准确率。由于各个行业负荷预测值求和时有部分误差会相互抵消，因此每个模型总负荷的MAPE 值均低于单个行业的MAPE值。进一步分析可以发现：

1）A 组的A1、A2、A3 模型虽然通过聚类处理提高了关联分析的准确性，相比于不经过聚类处理的B1模型预测准确率有较大提升。但因为聚类簇数k需要人为指定，无法根据不同外部影响因素和行业负荷数据的特点进行自适应变化，因而影响了聚类的效果，预测误差相比于采用优化kmeans聚类的本文模型也更大。

2）B组模型中，B1和B2模型的MAPE值相对较高，说明直接采用未聚类的标准互信息关联分析方法，或者Pearson相关系数，均难以准确地衡量外部影响因素与行业负荷之间的非线性相关性，导致行业负荷预测的精度受到影响。相比而言，B3模型的预测精度有所提高，可以较好地衡量非线性相关性，但由于Copula 函数的相关性分析结果会受到数据本身分布特点的影响，对不同行业负荷数据的适应性不足，整体上预测误差仍大于本文模型。

3）C 组模型中，不计及外部影响因素的C1 模型在所有模型中预测误差最大，说明外部影响因素对于各个行业负荷的变化均有较为显著的影响，仅利用行业历史负荷数据无法准确捕捉未来负荷的变化规律。C2 模型的MAPE 值整体上也比较高，说明在不计及外部影响因素关联分析结果的情况下，仅依靠机器学习模型自主学习不同外部因素对不同行业负荷的影响，仍难以较好地适应外部因素与行业负荷之间复杂多变的相关关系。

从表5可以看出，本文模型在各个行业负荷和总负荷预测的RMSE 值均为最小，说明本文模型的预测结果围绕负荷实际值的波动程度最小，负荷预测结果具有良好的稳定性。未考虑外部影响因素的对照模型C1在各行业负荷预测中具有最大的RMSE 值，表明对外部影响因素的分析对于跟踪行业负荷的变化有重要意义。另外，虽然对照模型B3 与本文模型在MAPE 值上最接近，但RMSE 值与本文模型仍有较大的差距，主要是由于本文模型除了能准确地分析行业负荷与温度、节假日的关联性，对相对湿度、降水量等次要影响因素的关联分析结果也较为准确，因此预测误差的离散程度更小，预测结果有更好的稳定性。

为了更直观地对比本文模型与各对照模型的预测结果差异，从测试集中截取48 h 的总负荷预测结果，其中前24 h 属于工作日，后24 h 属于节假日，绘制实际负荷曲线与各个实验模型的预测负荷曲线。对照模型组A、B、C与本文模型的对比结果分别如图4—6所示。

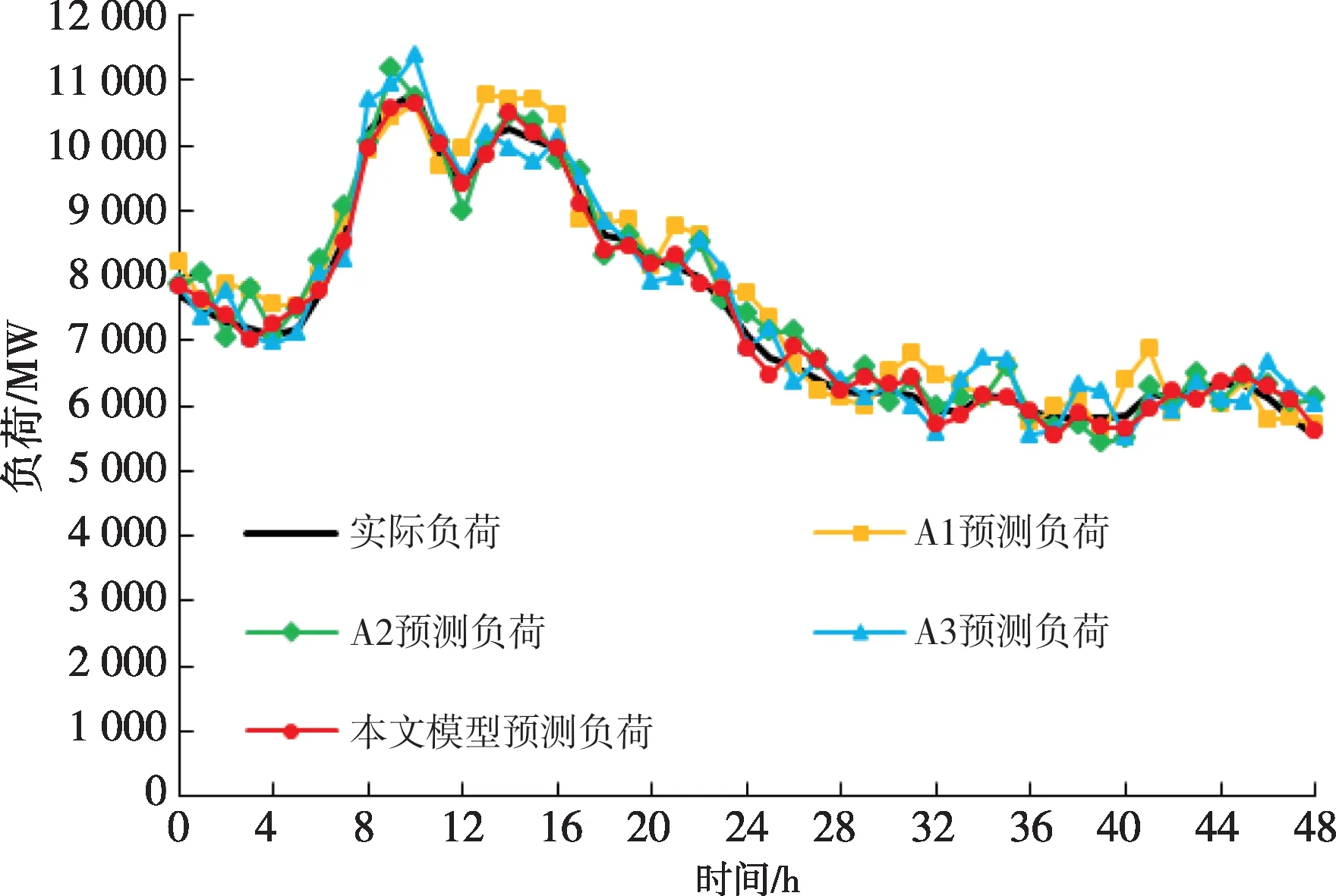
图4 对照模型组A与本文模型的对比结果Fig.4 Comparison results between controlled model group A and the proposed model

从图4可以看出，A1、A2、A3模型和本文模型均采用了“聚类+标准互信息”的改进关联分析方法，总负荷的预测曲线基本能够较好地跟踪实际负荷的变化趋势，但由于A1、A2、A3 模型的聚类方法未进行优化，进而影响了数据聚类效果和后续的关联分析准确性，因此相比于本文模型仍有更大的预测误差。

从图5 可以看出，本文模型和B3 模型能较好地模拟实际负荷曲线，尤其是在负荷高峰和低谷时能比较准确地跟踪负荷的变化，同时本文模型更少出现与实际负荷相差较大的预测点，因此RMSE 值相对于B3 模型有比较明显的优势；B1、B2 模型对行业负荷与外部影响因素的关联性分析不够准确，影响了负荷预测的整体精度，特别是在负荷高峰和低谷时难以准确跟踪负荷的变化。

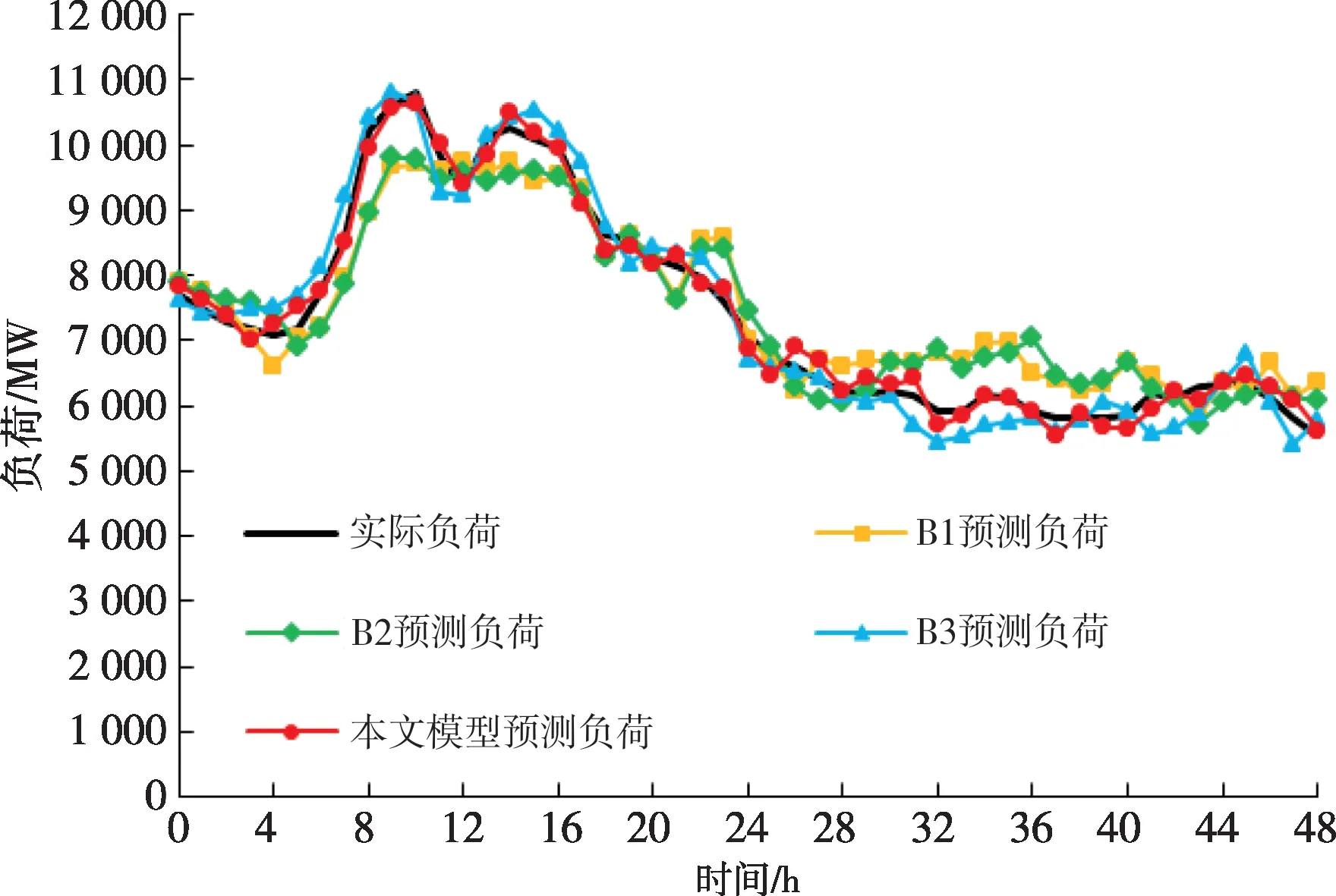
图5 对照模型组B与本文模型的对比结果Fig.5 Comparison results between controlled model group B and the proposed model

从图6 可以看出，C1 模型未计及外部影响因素的作用，只能从历史负荷中挖掘有限的信息进行负荷预测，无法有效捕捉到外部影响因素对各行业负荷的影响，因此预测负荷曲线与实际负荷曲线存在明显的偏差；C2模型虽有考虑外部影响因素，但未对外部影响因素与各行业负荷的关联性进行分析，负荷预测准确性与本文模型相比仍有较大差距。另外，为了说明本文模型在进行短期负荷预测时对不同行业的用户分别进行负荷预测的意义，另设计一个不区分用户所属行业的对照模型D1。D1的总负荷预测结果不通过各行业负荷预测值求和得到，而是采用第2、3 章的方法分析总负荷与各外部影响因素的关联性后，采用第4章的方法直接对总负荷进行预测。统计预测结果后得到相应的MAPE和RMSE指标如表6所示。