宽带噪声激励下含分数阶时滞系统的随机分岔*
2023-11-27盛正大王媛王慧男王芳
盛正大,王媛,王慧男,王芳
(兰州交通大学数理学院, 甘肃 兰州 730070)
0 引言
Van der pol系统是一种常见于数学与物理研究领域且具有清晰的动力学特征的经典电路系统,学者们对该系统的随机分岔行为进行了诸多研究. 例如,F.Moss等通过摄动分析研究了Van der pol 系统的线性稳定问题[1],结果表明分岔点相对于确定性的强度与噪声强度成正比;Mathieu等利用多尺度展开方法对于随机激励下的Van der pol系统的分岔阈值进行了解析确定[2];Shinji Doi等利用算子的密度演化方法分析了Van der pol系统的随机分岔[3];R. Mbakob Yonkeu等研究了指数相关噪声激励下的Van der pol系统的随机分岔问题[4]. 在广泛的应用和研究中,学者们发现时滞会对Van der pol系统产生明显的影响,如时间延迟引起的震荡、混沌和周期运动可能会导致工程的失败[5-6],但恰当选取时滞参数可以提高对于系统的控制,因此在Van der pol非线性系统中补充时滞反馈具有重大意义. 王明芬研究了时滞Van der pol方程hopf分支的等价性[7];岳锡亭等考虑到电子震荡的滞后性,在原有的研究成果上加入了时滞,并提出了含时滞项的Van der pol方程,研究了周期扰动下的含有时滞项Van der pol系统在特定的参数条件下产生的临界分支,且证明了时滞项对振幅存在影响,但岳锡亭的研究仅仅局限在狭义Van der pol系统中[8-9]. 付守才等在文章中讨论了时滞Van der pol系统的hopf分岔,提出了分支解稳定的参数条件[10]. M.M.Klosek利用多尺度方法对于带有时滞的Van der pol系统进行了随机分岔分析[11]. M. Gaudreault分析了在时滞参数较小时的随机分岔阈值[12]. 可见学术界对于Van der pol系统的研究相对完善,但这些研究大多限于整数阶非线性系统.相较于整数阶,分数阶的优势在于拥有良好的记忆性,并且利用分数阶微积分所建立的模型更加适用于真实世界,更符合现实存在的粘弹性阻尼、生物神经元等的物理特性[13-16]. 有关含分数阶时滞反馈的Van der pol系统产生随机分岔现象的研究还较欠缺. 因此本文研究了在宽带噪声的激励下含分数阶时滞耦合反馈的Van der pol系统的随机P-分岔现象.
1 模型处理
研究宽带噪声激励下含有分数阶时滞负反馈的Van der pol系统:
(1)

(2)
ξ(t)为宽带噪声,功率谱密度如下:
(3)
设φ(t)=ωt+θ,令式(1)的解为
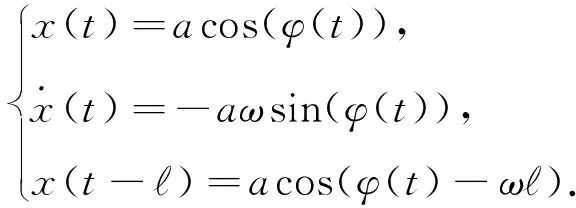
(4)
对式(4)进行计算,可得
(5)
(6)
(7)
将式(4) 和式(7)代入式(1)中,可得:
(8)
又从式(6)知
(9)
将式(9)代入式(8)中,可得
(10)
通过上述代换,式(1)可以用下面的微分方程表示:
(11)
2 平稳概率密度函数
将式(11)写为如下形式:
(12)
其中
(13)
(14)
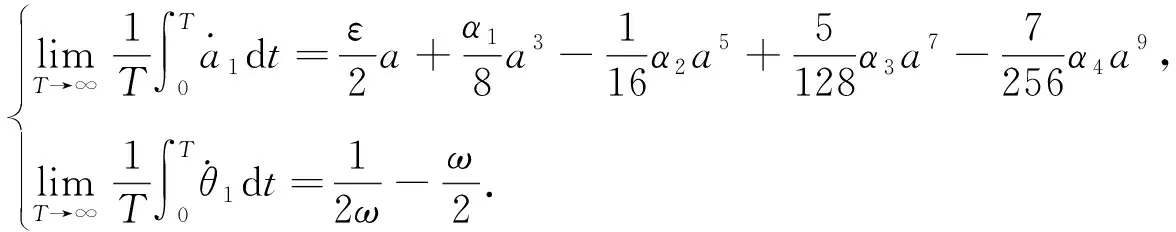
(15)
(16)
故将Caputo形式的分数阶微分Dαx(t)写成双积分形式
(17)
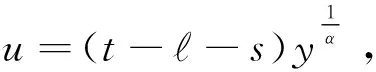
(18)
则式(18)满足
(19)
将式(4)代入式(19)中
(20)
从式(20)解得:
(21)
其中c是根据初始条件ψ(y,0)=0来决定的,进一步将式(21)代入式(19)中得:
(22)
(23)
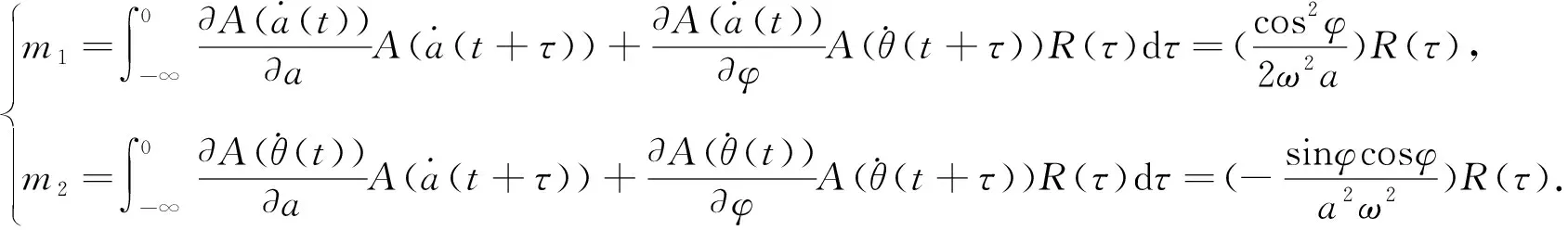
(24)
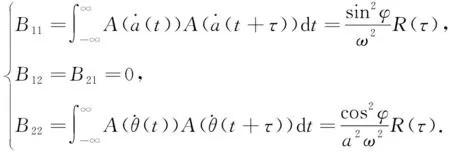
(25)
(26)
根据式(24),式(25)和式(26)得如下It随机微分方程:
(27)
W(t)是标准的维纳过程,且da不依赖于θ,因此可得系统幅值的FPK方程:
(28)
其中:
(29)
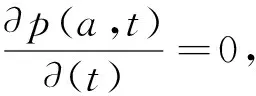
(30)
其中C是归一化常数.
3 仿真分析
3.1 时滞参数对随机P-分岔的影响
设所添噪声各系数值ζ=1,ω=0.9,ω1=0.3和噪声强度D=0.1,固定所研究系统的参数值α1=1.51,α2=1.25,α3=1.25,α4=0.5,分数阶α=0.3,选取时滞参数=0.01,绘制出相应的联合概率密度函数图(图1(a)),及其俯视图(图1(b)),截面图(图1(c)),平稳概率密度函数图(图1(d)).

(a)联合概率密度分布图 (b)联合概率密度俯视图
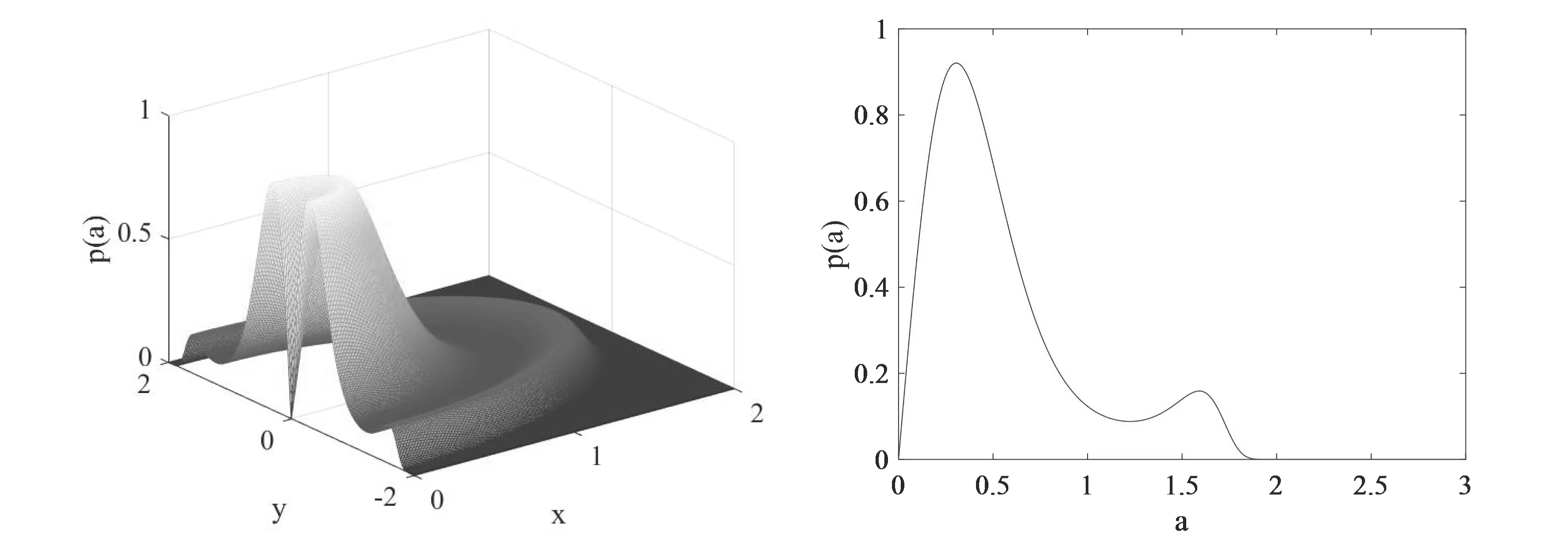
(c)联合概率密度截面图 (d)平稳概率密度函数图
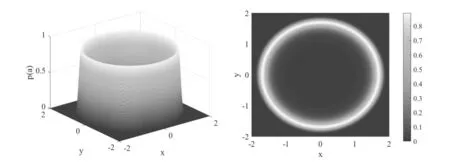
(a)联合概率密度分布图 (b)联合概率密度俯视图
通过图2可以得出,固定噪声和系统的其他参数,仅改变时滞参数.当选取的=0.01,可在联合概率密度函数图中看到一个明显的双峰曲线.当时滞参数值增加为=0.2,可以从平稳概率密度函数中看到一个先递增再递减的单峰曲线.与此同时,联合概率密度函数图的峰形也发生了变化,由双峰变为单峰.说明当固定其他参数不变,时滞值从0.01增加为0.2时,平稳概率密度峰值发生变化,出现单峰和双峰之间的跃迁.
3.2 分数阶α对随机P-分岔的影响

(a)联合概率密度分布图 (b)联合概率密度俯视图
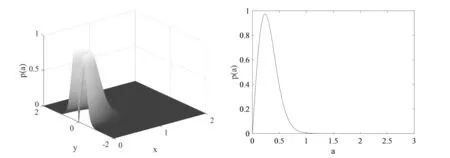
(c)联合概率密度截面图 (d)平稳概率密度函数图
4 结论
研究表明在宽带噪声的激励下,固定其他参数不变,仅改变时滞参数的大小,平稳PDF曲线会出现从双峰到单峰的变化,系统产生了随机P-分岔;而仅改变分数阶阶数,平稳PDF曲线同样出现从双峰到单峰的峰值变化,系统会随着分数阶的变化出现P-分岔现象.
