改进COOT算法求解多目标柔性车间调度问题

凌方平，吉卫喜

江南大学 机械工程学院，江苏 无锡214122

柔性作业车间调度问题（flexible jobshop scheduling problem，FJSP）隶属于NP-Hard 问题，是Bruker 等[1]在1990年建立的，它是调度问题中新的分支。此类问题旨在充分利用有限的生产资料，协调生产部门间的需求，同时最大化生产获益。现阶段离散制造企业中，车间对加工工件的机器和人员配置是灵活的、多样的，因此FJSP 相较流水车间调度和普通作业车间调度，能更好地契合该生产实况，探讨和解决FJSP具有重要意义。

元启发式算法通过制衡全域搜索与区域搜索能力，能出色地寻优求解NP-Hard 问题。单目标FJSP 的优化目标单一，大多根据完工时间比较不同调度方案的优劣。诸多元启发式算法一定程度上能在全局进行搜索，在短时间内得到此类问题的最优解或最优解的近似解。连裕翔等[2]以最大完工时间为优化指标，为Jaya算法设计了迭代候选解集和新的邻域结构，最后用基准实例集证明了改进Jaya算法的有效性。

然而在现实的生产作业中，车间常会有其他考虑的方向，因此多目标FJSP 应运而生。求解多目标FJSP 常见的手段有两种：一种对各个目标赋予权重后加权计算，再用类似处理单目标FJSP 的方法进行解决。陈浩杰等[3]针对不同的资源受限情况，分类设计了归一化方式，并改进了遗传规划算法来解决问题；Zhang等[4]在粒子群算法的基础上，结合禁忌搜索算法来接近最优解，从而化解了大规模多目标FJSP。还有一种是使用Pareto思想的优化策略。由Knowles等[5]构建的多目标问题演化策略PAES、由Deb等[6]提出的把遗传算法与非支配排序结合的NSGA-II 算法，常被学者进行改进，并用来求解多目标FJSP。例如肖世昌等[7]提出了多目标混合分布估计算法，得到了兼顾调度性能和鲁棒性的Pareto 解集；鞠录岩等[8]考虑了运输时间的影响，使用改进的NSGA算法求解多目标FJSP。

COOT 算法是一种根据鸟类群体行为提出的元启发式算法，由Naruei 等[9]在2021 年提出，初衷是解决单目标问题，具有收敛速度快、参数设置简单、个体更新方式多样的优点。该算法虽然刚出现不久，但目前已被用于求解各种优化问题[10-11]。然而，COOT 算法应用在生产调度领域的文献极少，且算法性能仍有改进的空间。因此，本文将COOT 算法扩展应用于FJSP，并对COOT算法进行了一系列的改进。

针对以上不足，本文构建了以最小化最大完工时间、机器总负荷、耗能为优化目的，且考虑了机器与工人柔性因素的车间调度模型。接着设计编解码方式，确保个体位置信息与更新方式均为连续值的COOT 算法能被离散型的调度问题使用。然后通过引入存档集和Pareto 解的概念，使得原先只能解决单目标问题的COOT算法，拥有了解决多目标问题的能力。还改进了算法中特定个体的更新方式以加快收敛速度，并更改其邻域搜索方式，同时配合SA的思想，避免算法陷入局部最优。最后通过算例进行测试，以证明MOCOOT-SA的有效性。

本文的主要贡献是：一是改进了COOT 算法，使之能解决多目标问题。二是在FJSP的多目标权重难以确定的情况下，提供了解决思路和方案。

1 问题描述与模型建立

本文的多目标柔性车间调度问题描述如下：工厂现有l个工人L={L1,L2,…,Ll},要在m个机器M={M1,M2,…,Mm} 上制作n个工件N={N1,N2,…,Nn}，工件的工艺路线是固定的、已知的，工件Ni有j道工序{Oi1,Oi2,…,Oij}，Mij⊆M和Lij⊆L分别是能加工工序Oij的机器和人，同一工序选择了不同的机器或者人，导致它的加工时间可能不同。调度的目的是把每个工件的工序合理分配给工人，并安排工人在机器上加工，让优化目标尽可能达到最优。

建立问题模型时，根据实际的加工情况，提出若干约束条件：

式（1）～（8）中，m为总的机器数，l为总的工人数，gi为工件i的总工序数，p为机器号，q为工人号，Sij为工序Oij的开始时间，Eij为工序Oij的结束时间，BTp为机器p的开机时间，CTp为机器p的关机时间，tijpq为工序Oij在机器p上被工人q加工所需的时间，Z为足够大的正数。αijpq、βijrsp、γijrsq为0～1决策变量：如果工序Oij在机器p上被工人q加工，则αijpq=1，否则αijpq=0；如果工序Oij与Ors都在机器p上加工，且Oij先于Ors，则βijrsp=1，否则βijrsp=0；如果工序Oij与Ors都被工人q加工，且Oij先于Ors，则γijrsq=1，否则γijrsq=0。

式（1）表示每个工序的加工过程不会中断，工序的完工时间等于开工时间加上加工所需时间；式（2）表示每个工序仅加工一次，且只能选一个工人和机器；式（3）表示只有在上道工序完成后，该工件才能开始下道工序的操作；式（4）表示所有机器在0时刻都已开动，且可以被使用；式（5）表示每个机器在任何时间点只能加工一个工序；式（6）表示每个工人在任何时间点只能加工一个工序；式（7）表示所有工序的开工时间、完工时间和加工时长都是非负数；式（8）表示任何一个机器，只有在完成了所有分配给它的任务后，才能关机。

调度的优化目标有三项：最大完工时间f1，机器总负荷f2，总耗能f3。以此建立数学模型，目标函数为：

式（9）～（11）中，n为工件的总数，Di为工件i的完工时间，PYp为机器p的负载功率，PNp为机器p的空载功率。

2 编码与解码

2.1 编码

标准COOT算法的初衷是解决连续性问题，而调度问题中机器、工序、人员的选择都是离散的，因此直接用标准COOT算法来解决FJSP是无法实现的。编码的方式在一定程度上影响算法的性能，本文选择了基于工序的编码方式。算法中的种群个体由位置向量表示，向量的长度为，其中每个值的取值范围为0至1间的随机数，它与工序的对应关系如图1 所示。例子中共有3工件7工序，先将位置向量与有顺序的工序编码进行映射，再将原向量升序排序，工序编码随之移动，得到的[2 2 3 1 3 2 1]中，以工件2 为例，出现第几次2 就代表是工件2的第几道工序。如此，就得到一个有效的工件序列，记作List。

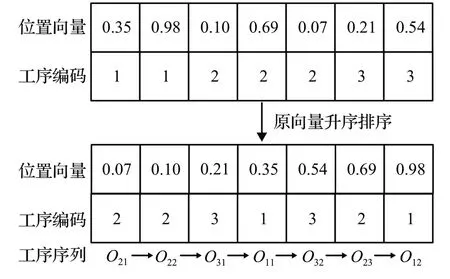
图1 编码样例图Fig.1 Coding sample map

这种编码方式简洁明了，还确保了所有个体的位置信息都能转化成合法的调度方案。

2.2 解码

本文考虑了机器与工人的约束，采用了插入式贪婪的解码方式。效仿文献[12]提出的中继卫星调度任务构成的时间窗口概念，把FJSP 中每个机器或者工人空闲的时间段称为时间窗口集。时间窗口集是若干个不重叠的时间窗口[ ]t1,t2的并集，并给出如下定义：时间窗口集a与时间窗口集b相重合的时间段c，记作c=a∩b。

解码方式如下：

（1）以集合Rn记录各工件最后一道已完成工序的完工时间，Rm、Rl分别记录各机器、工人的时间窗口集，从List中选择加工优先度最高的工序Oij。

（2）获取可加工Oij的设备集合Mij，设其中有x1个机器；获取可加工Oij的工人集合Lij，设其中有x2个工人，则对于两者的选择共有x1x2种组合。对于每种组合，可知工件在该组合的情况下所需的加工时长t。从Rm中取对应机器的时间窗口集Um，从Rl中取对应工人的时间窗口集Ul，求得交集U=Um∩Ul，再从Rn里得到此工件的上道工序完成时间Ei(j-1)（若Oij是工件i的头道工序，该值取0）。从U中按时间先后顺序，找到其中第一个符合Ei(j-1)时刻且长度不小于t的时间窗口。一旦找到这种时间窗口[t1,t2]，即可得知在此种机器、工人组合下，Oij的加工时间为[t1,t2+t]。同理，分别计算其他组合情况所对应的加工时间。

（3）以最早完工的原则，取得该工序所有组合情况中的min(t2+t)，它对应的机器与工人就是此工序最后确定使用的。

（4）更新Rn、Rm、Rl，从List中选择下道工序，循环步骤（1）～（3），直至遍历全部工序后，按式（9）～（11）计算f1至f3。

3 基于MOCOOT-SA算法的模型求解

3.1 标准单目标COOT算法

COOT算法的原理为：用搜索空间中分布的散点模拟自然界中白骨顶鸟个体，将搜索过程模拟成白骨顶鸟在水面上集体运动的过程，把问题的目标函数模拟成白骨顶鸟所在位置的优劣。

该算法主体思想如下：

（1）初始化种群，随机选取其中NL个成为leader，剩余的NC个为coot，比例常取1∶10，把所有coot 平均分配给每个leader 形成一组，共NL组，并根据适应值确定全局最优。

（2）每个coot 有三种运动方式，按其中一种更新位置。

（3）每个coot 更新后的适应值优于所在组的leader时，交换两者。

（4）每个leader 向全局最优的邻域移动。

（5）每个leader 更新后的适应值优于全局最优时，交换两者。

（6）重复（2）至（5）直到满足结束条件。

该算法主要仿生了如下的移动方式：

（1）coot 根据所在组的leader 调整位置

式中：CootPos(i)为某个coot 的位置；LeaderPos(k)为该coot 服从的leader 位置；R和R1是随机值。

（2）coot 跟随前一个coot 链条移动

（3）coot 随意移动

式中：A=1-L/Iter,L为当前迭代次数，Iter为最大迭代次数；R2是随机值；Q是全局随机一点。

（4）leader 向全局最优的邻域移动

式中：LeaderPos(i)为某个leader 的位置；gBest是全局最优位置；B=2-L/Iter；R和R3是随机值。

3.2 结合SA的多目标COOT算法

3.2.1 存档集的引入

在单目标COOT算法中，易通过比较得到全局最优值。然而在多目标问题中，除了一个解的各目标值均劣于另一个解的情况外，不能严格地区分两个解的优劣。为此，在多目标COOT 算法中，引入存档集的概念，当leader 要向全局最优的邻域移动时，改为向存档集中随机一个邻域移动。设存档集的大小为C，存档集的建立步骤如下：

（1）将上一代的存档集与当代种群合并，筛选出目标函数值不重复的个体（若为初代，则改为对初代种群执行此操作）。对合并的种群进行非支配比较，筛选出Pareto最优解集。

（2）若Pareto 解集中解的个数不大于C，则该解集成为新的存档集。

若个数大于C，则先令解集中所有个体的初始拥挤度I为0。再把这些解按每个优化目标函数值的大小排序。特别的，边界上解的I为无穷大，然后按下面式子计算解集中其余每个解的拥挤度I：

式中：x是要优化目标的个数；分别为第i个解的前一个与后一个解的第d个目标函数值；为第i个解在第d个目标函数的最大值与最小值。I越大，说明该解附近的解就越少，与其他解的相似程度越低，对种群的多样性能作出更大的贡献。

最后按拥挤度排序，依次从解集中删除拥挤度最小的解，直至解集的个数为C，令此解集成为新的存档集。

3.2.2 边界变异

在COOT算法迭代寻优的过程中，种群中个体的位置随着变异操作，会有越出搜索域的可能，这样的个体称为无效个体。原COOT算法中的处理方法如下：若个体的某个维度在变异后超过了该维度所定义的上（下）限，则令该维度的值修正为上（下）限。这种做法会让个体在搜索域的边界上聚集，个体的随机性变低，算法的局部搜索能力下降，为此采用如下式子处理个体在某个维度上的越界：

式中：ub和lb为搜索区域在维度d的上限和下限；m通常取0.01至0.1；xd为越界修正后在维度d的值。

3.2.3 自适应选择系数

COOT 算法中，已知当前迭代次数为i，选择概率p1、p2均为固定值0.5，coot 个体选择的更新方式及其概率如图2所示。

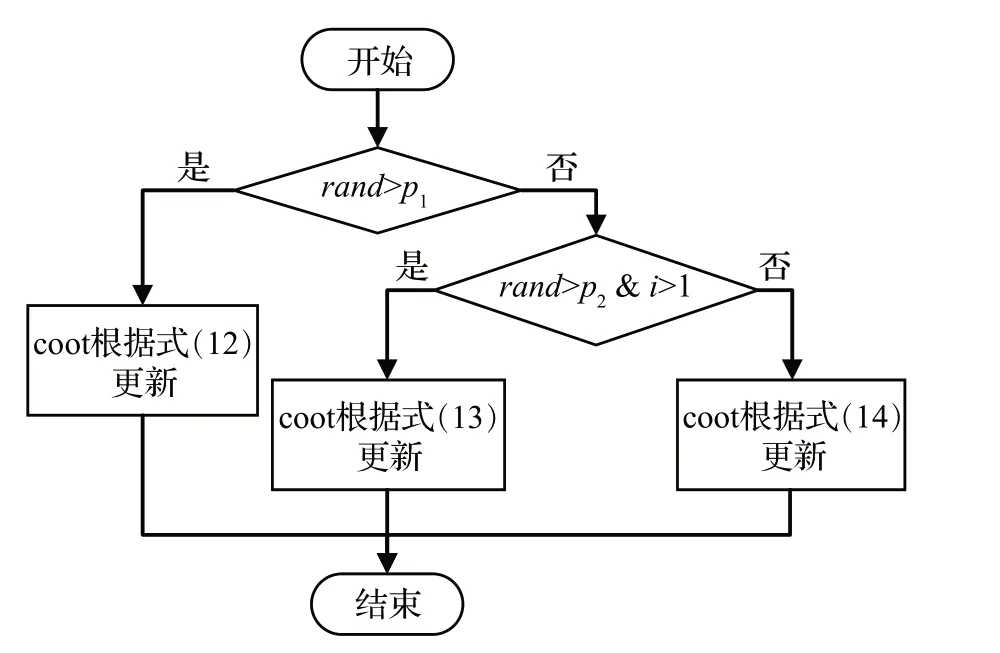
图2 coot个体选择的更新方式及概率Fig.2 Update method and probability of coot selection

基于群体的元启发式算法的搜索权重往往是动态变化的[13-14]，以利于算法跳出局部，尤其在算法运行的后期很重要。因此，本文对p2进行了自适应调整修改。为此，定义了两个参数：聚集度因子ω和进化速率因子φ。

聚集度因子ω定义为：

式中：d为优化目标的个数；分别为第i次迭代中，存档集的所有解与种群的所有解在某个优化目标上适应度的均值；ω体现了当前种群所有个体的聚集程度，0＜ω≤1。

进化速率因子φ定义为：

式中：d为优化目标的个数；分别为第i次与第i-1 次迭代中，存档集的所有解在某个优化目标上适应度的均值；φ体现了种群的进化速率，0＜φ≤1。

当ω变大时，体现了种群的聚集程度变高，有进入局部最优的风险，此时要使p2增大，提升coot 个体移动的随机性，扩大其搜索区域，以强化算法的全局搜索能力；当φ变大时，体现了种群的进化速度逐渐变小，此时需要减小p2，使得coot 个体在更小的区域内搜索，进而充分搜索局部找到最优解。

结合上述讨论，将固定值p2更改为自适应选择系数,应为ω与φ的函数，表示为：

式中：当ω取0.10～0.25，φ取0.40～0.60 时，算法的性能较好。

3.2.4 改进leader的更新方式

在COOT算法中，种群中两类个体的更新方式有较大差异。coot 的更新方式有三种，且个数相较leader 众多，有较强的全局搜索能力。

对比之下，leader 的更新方式有三个缺点：（1）只有式（15）一种更新方式，局部搜索能力一般，且更新后的位置如果劣于原leader，则不会被接受，进一步降低了搜索能力，使得陷入局部最优的可能性增大。（2）leader是通过向已知的全局最优移动，全局最优再向真实的Pareto前沿移动的方式来更新的，一定程度上降低了算法的收敛速度，如图3 所示。（3）COOT 算法适用于解决连续的实数问题，式（15）是在笛卡尔空间中对leader 的邻域进行搜索，解码后映射到离散的调度方案时，不能保证解码后是有意义的邻域。因此，本文改进了leader的更新方式。

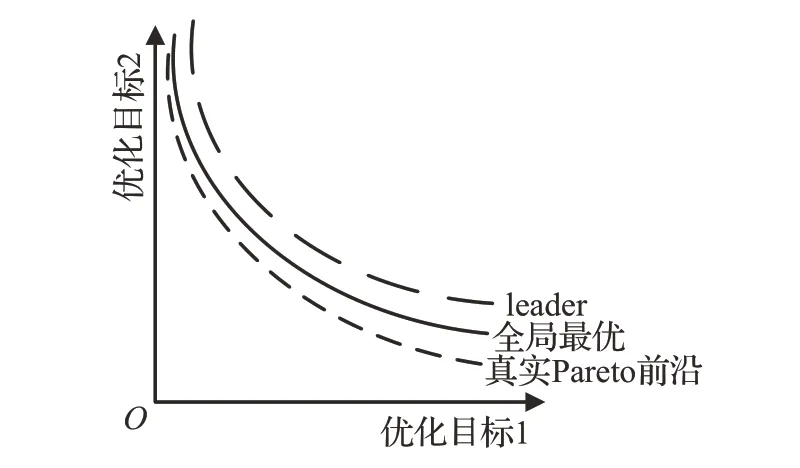
图3 leader更新示意图Fig.3 Leader update diagram

首先，每个leader 更新时仍按式（15）搜索gBest 的邻域生成一个临时解tem,若tem 支配leader,则tem 替代对应的leader，否则从存档集中随机选取一个取代该leader。这个操作虽然加快了收敛速度，且保证了新的leader 是已知解里面的最优解之一，但增加了陷入局部最优的风险。作为代偿，引入了SA 对leader 进行邻域搜索，并对leader 的邻域定义进行调整。leader 邻域的新定义是调换向量leader 上任意两个位置上的值，对应到工序序列的变换就是调整任意两个工序的位置，如图4所示。对新的工序序列进行插入式贪婪解码，就得到了新的调度方案。

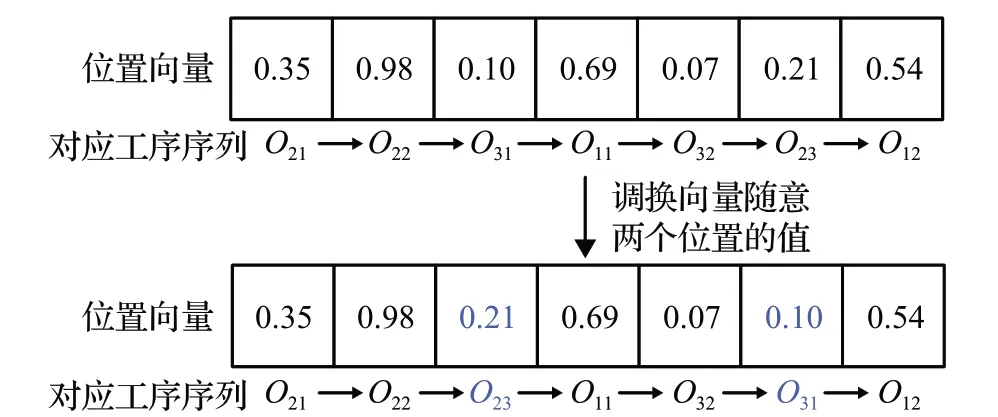
图4 个体leader的某个邻域图Fig.4 Neighborhood graph of leader

SA 算法具有局部搜索能力强的优点[15]，在初始温度足够高、结束温度足够低、退火速率足够慢的情况下，理论上能获取全局最优解，缺点是迭代次数过多导致的算法运行时间长，因此不能直接使用。

在使用SA 对leader 邻域搜索时，也会出现两个解互不支配的现象，进而引发难以比较优劣的问题。常见的方法是赋予权重后进行比较，或者在出现互不支配的情况时，随机选取一个[16]。本文参考SUMAN[17]对SA算法提出的Pareto支配适应度值的改进接受准则，按如下计算的概率接受新解：

式中：T为当前退火温度；Sold、Snew分别是旧解和新解的适应度值，适应度值等于档案集中支配该解的个数。

在式（21）中，分子的大小与档案集的规模有关，因此初始温度不宜过高，取档案集大小的1/2 左右既能避免陷入局部最优，又能一定程度上缩减迭代次数，减少SA算法运行时间过长带来的弊病。

3.2.5 算法流程

结合上述改进，构建MOCOOT-SA算法。其中的参数设置：种群规模N（其中leader 类个体有NL个，coot类个体有NC个），初始选择系数p1、，最大迭代次数Iter,档案集最大容量Nr，模拟退火初温Ts，终温Te，降温系数δ，马尔可夫链长度lm。MOCOOT-SA 算法的流程图如图5所示。

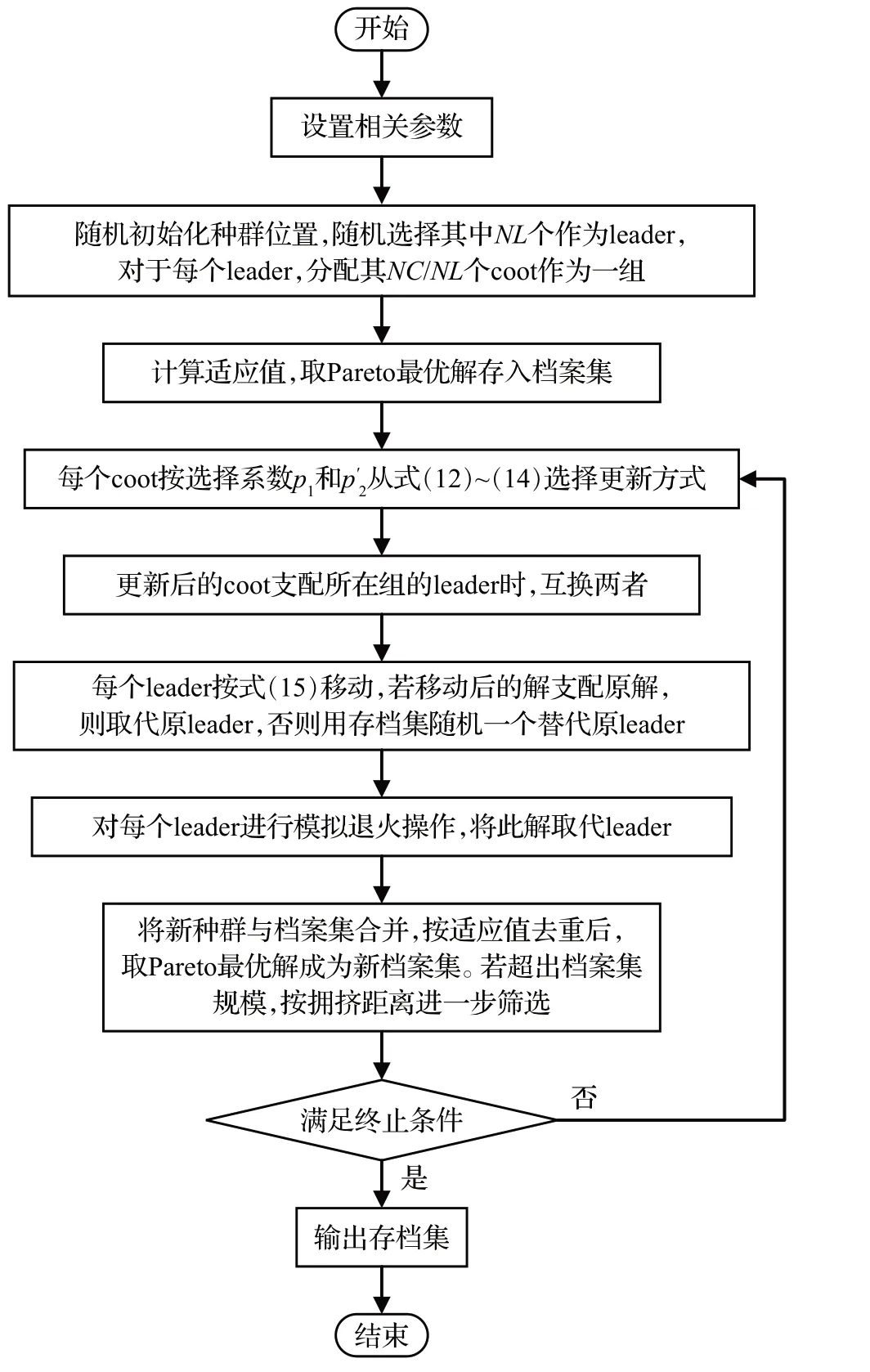
图5 MOCOOT-SA算法流程图Fig.5 MOCOOT-SA algorithm flow chart

4 实验结果与分析

为了验证MOCOOT-SA算法的有效性与可行性，本文在MK01基准算例（10工件6机器）的基础上，结合实际，给出了机器与工人的信息，数据如表1～表2 所示。表1 是5 个工人与6 个机器的关系，符号○代表当前工人能操作该机器。表2 是6 个机器的耗电情况，机器在负载与空载的情况下耗能不同。

表1 各工人能加工的机器信息Table 1 Machine information that each worker can process

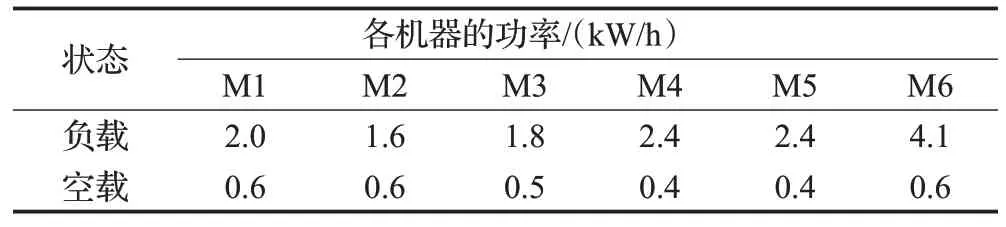
表2 机器的耗能信息Table 2 Machine energy consumption information

对MOCOOT-SA 算法运行上述例子，参数设置如下：种群规模N=100（其中leader 类个体有10个，coot类个体有90 个），选择系数p1=0.5，自适应选择系数0.5+0.1h-0.4g，档案集最大容量Nr=30，最大迭代次数Iter=150，模拟退火初温Ts=15，终温Te=0.3，降温系数δ=0.85，马尔可夫链长度lm=100。

多目标粒子群算法（MOPSO）、NSGA-Ⅱ算法分别是在成熟的粒子群算法和遗传算法上进一步改进得到的，两者突出的寻优能力使它们常被应用到调度问题中[8，14]。为了比较新算法的性能公平起见，尽量使得三种算法的种群个数和迭代次数等保持一致。MOPSO的有关参数如下：最大迭代次数为200，种群规模为100，档案库大小为50，初始惯性权重系数为0.9，惯性权重衰减为0.99，个体学习因子为1.7，全局学习因子为1.8；NSGA-Ⅱ的有关参数如下：最大迭代次数为200，种群规模为100，交叉概率为0.9，变异概率为0.03。实验结果如表3所示。

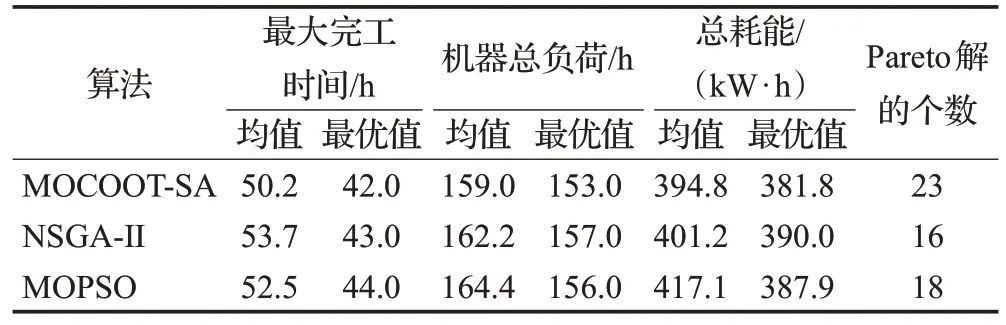
表3 三种算法结果Table 3 Three algorithm results

由表3的信息得知，通过MOCOOT-SA得到的Pareto解总体上不劣于其他两个算法：与NSGA-Ⅱ比较Pareto解的均值，最大完工时间优化了3.5 个单位，优化比为0.065，机器总负荷优化了3.2个单位，优化比为0.020，总耗能优化了6.4个单位，优化比为0.016；与MOPSO比较Pareto解的均值，最大完工时间优化了2.3个单位，优化比为0.044，机器总负荷优化了5.4个单位，优化比为0.033，总耗能优化了22.3个单位，优化比为0.057。同理，比较MOCOOT-SA与NSGA-Ⅱ算法在各目标上的最优值，均有提升，优化比为0.023、0.025、0.021；比较MOCOOT-SA与NSGA-Ⅱ算法在各目标上的最优值，优化比为0.045、0.019、0.016。同时，在同等种群规模的前提下，通过MOCOOT-SA 得到的Pareto 解的数量要比另外两个算法多，能给予工厂更丰富的选择，可见MOCOOT-SA 算法有解决FJSP问题的能力。

用MOCOOT-SA 算法仿真后得到的存档集的解共有23组，如表4所示。决策者可根据表4中的解和各自的偏好，选取一个作为最终的调度方案。

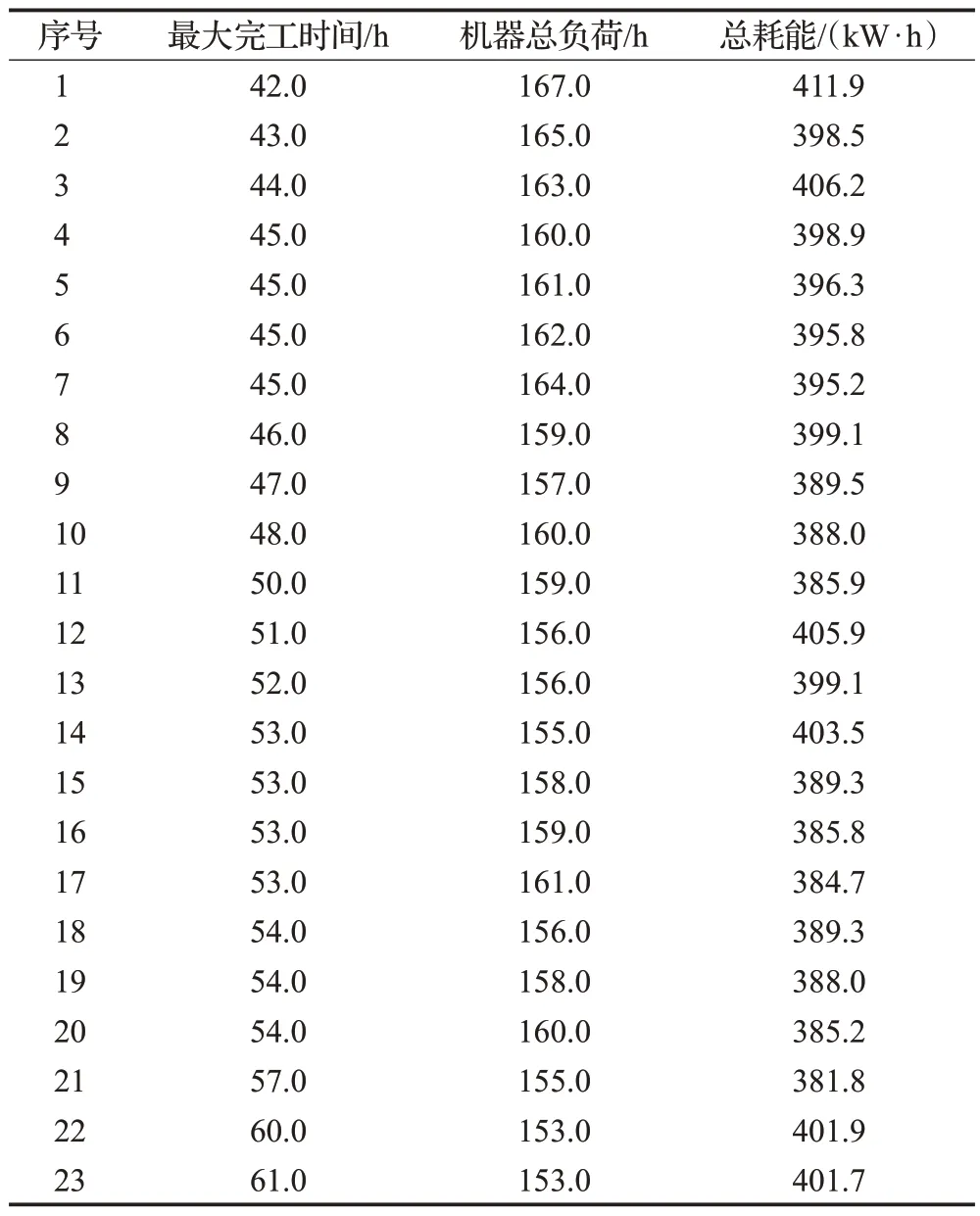
表4 最后一代时存档集的解Table 4 Solution for archive set in last generation

MOCOOT-SA算法求解该问题迭代至最后一代时，种群的解与存档集的解的分布如图6所示，证明了使用SA对leader 进行邻域搜索的有效性。

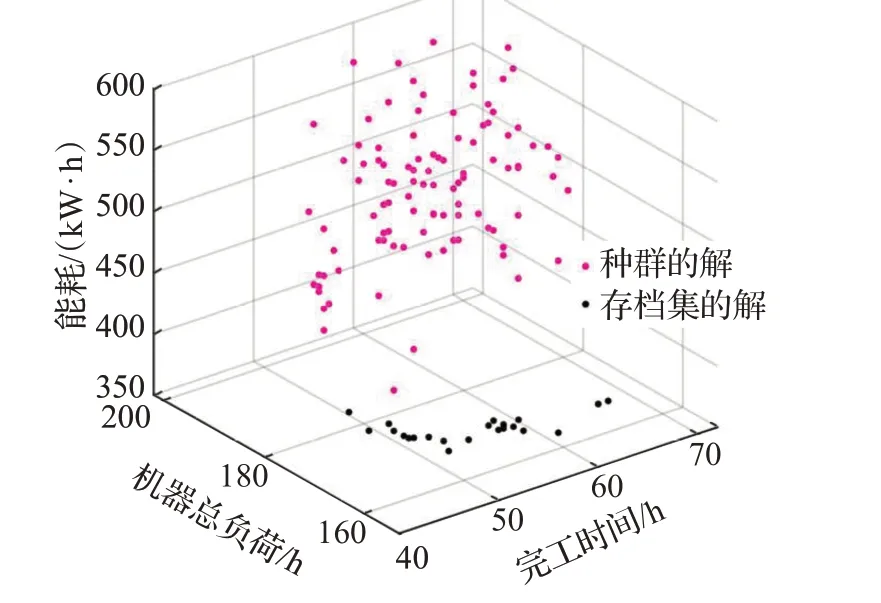
图6 种群与存档集的个体分布图Fig.6 Individual distribution graph of populations and archive sets

存档集中各目标适应值的迭代过程如图7所示，体现了存档集中所有解的最值与均值随迭代次数变化的情况。

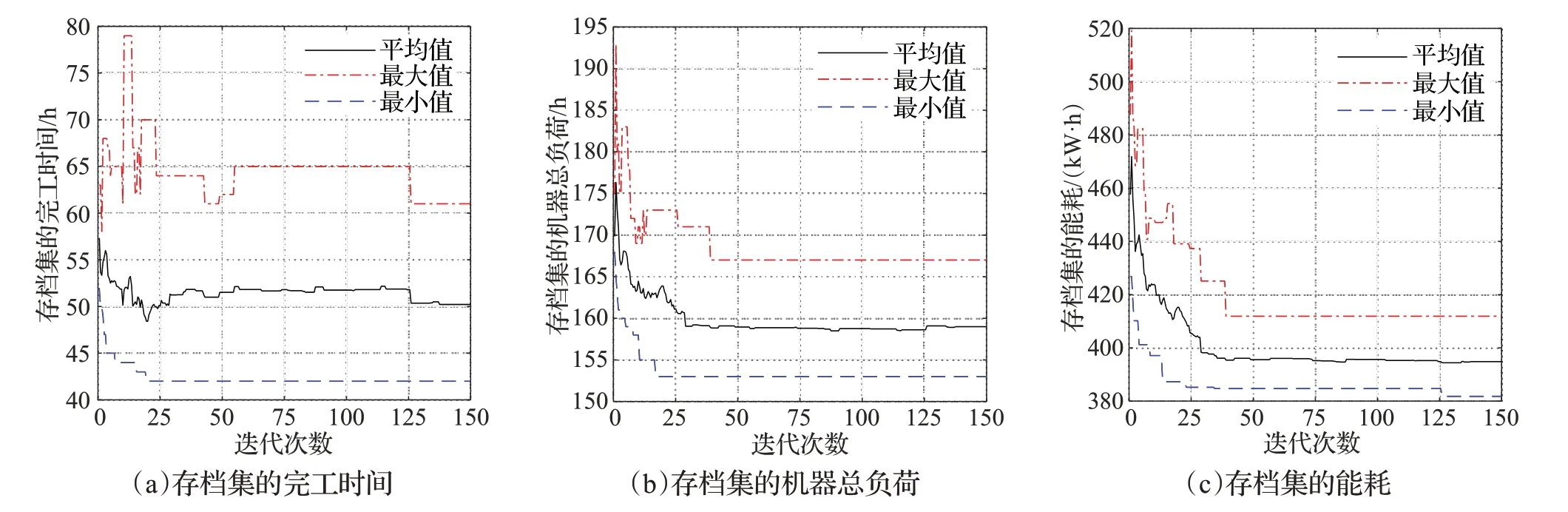
图7 存档集的解的变化图Fig.7 Variation graph of solution for archive set

图8 是表4 中第一个解的调度方案。以M6 的第一个工序上注明的10/1 5为例，表示工件10的第1道工序由工人5在第6个机器加工。按这种方式可依次获得所有工序的加工安排。

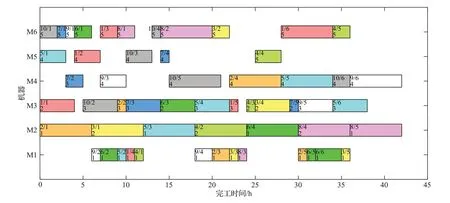
图8 调度甘特图Fig.8 Scheduling Gantt chart

5 结束语

本文考虑了机器与工人的约束，以最小化最大完工时间、机器总负荷、能耗三个优化目标，对多目标柔性调度车间问题建立了数学模型，并使用了简洁的编码方式，在解码过程中采用了时间窗口的概念，使得离散问题能在连续性算法上适用。同时，对单目标COOT算法进行了多方面的改进，以适应求解多目标问题和FJSP问题，得到了性能更好的MOCOOT-SA 算法。最后，通过算例测试，对MOCOOT-SA与NSGA-Ⅱ算法、MOPSO算法的方案进行比较，其各目标上的平均值的优化比为0.013～0.047，各目标上的最优值的优化比为0.016～0.045，证明了新算法的有效性。

在下阶段的研究进程中，可以考虑更多的约束条件，例如工装与刀具，并探索MOCOOT-SA 解决扰动环境下车间调度问题的能力。