舰船柴油机微通道内燃油空化现象的模型对比

李子铭, 刘振明, 刘景斌, 陈萍

(海军工程大学 动力工程学院, 湖北 武汉 430033)

0 引言

作为现代舰船柴油机的主要发展方向,高速高功率密度柴油机具有高喷射压力、高转速和喷油持续期短等特点[1-2]。随着高压共轨系统中的喷射压力不断提高,喷油器喷孔内部的空化问题愈发严重。当喷孔进出口压差较大时,喷孔内流道近壁面处会产生低压区,致使该区域内的高速燃油压力迅速降至其饱和蒸气压力值,导致空化现象的出现。喷孔内的空化不仅影响后续的喷雾燃烧效果,而且长期的空化腐蚀会导致喷孔内壁脱落,进而影响喷油精度和柴油机运行可靠性。目前,使用计算流体力学(CFD)方法验证相关的喷孔燃油空化流动试验,进而研究喷油器喷孔内的空化问题,是舰船柴油机领域中的研究热点之一。

当前广泛用于验证数值模型计算可靠性的燃油空化试验主要有Sou等[3]提出的二维喷孔试验和Winklhofer等[4-5]提出的微通道试验。由于微通道试验更接近实际的喷孔工作情况,近年来国内外学者们将其广泛应用于各类新型的喷孔数值模型验证中。Dai等[6]将Winklhofer试验用于弧形结构喷嘴模型可靠性的验证,并利用该模型研究了喷嘴弧度对喷孔内瞬态空化特性的影响,发现喷嘴弧度可显著降低孔内空化程度,弧度越大,空化程度越小,喷孔出口平均速度越小,但质量流量变化不大。通过结合Winklhofer试验数据,Sa等[7]在计算中使用了Realizablek-ε(k为湍动能,ε为耗散率)湍流与Schnerr-Sauer(SS)空化组合模型(简称Realizablek-ε+SS模型),验证了所构建多相流模型的空化分布与试验一致,进而定量研究了喷油器针阀上螺旋反槽结构对孔内燃油湍流流动及后续燃油喷射雾化过程的影响。Cristofaro等[8]使用大涡模拟(LES)模型计算发现所构建的多相流模型的空化分布与试验一致,并研究了液体燃料黏度对微通道节流流动时质量流量、速度曲线和空化分布的影响。Zhao等[9]使用网格尺寸为30 μm的模型验证了模型的空化分布、出口质量流量和截面速度分布与试验相近,最终研究了燃油的可压缩性对燃油在喷孔中排放系数和临界空化数的影响。Guo等[10]使用齐次松弛模型(HRM)和重整化群(RNG)k-ε湍流模型计算验证了所用模型与试验中的出口质量流量和空化分布误差极小,研究了针阀运动对喷嘴内空化发展的影响。

目前在研究Winklhofer试验时虽然能够获取到与试验现象较接近的数值计算结果,但因为所使用的计算模型和网格划分策略不尽相同,计算模型选取对计算结果和试验验证的影响尚无报道,影响机理尚未探明,导致模型验证策略尚无规律可循。

本文使用CFD计算软件,基于剪切应力输运(SST)k-ω(ω为比耗散率)与Zwart-Gerber-Belamri(ZGB)组合模型(简称SSTk-ω+ZGB模型)、SSTk-ω与SS组合模型(简称SSTk-ω+SS组合模型)、Realizablek-ε与ZGB组合模型(简称Realizablek-ε+ZGB模型)、Realizablek-ε+SS模型、重整化群(RNG)k-ε与ZGB组合模型(简称RNGk-ε+ZGB模型)、RNGk-ε与SS组合模型(简称RNGk-ε+SS模型)6种湍流和空化模型组合,依次对Winklhofer微通道试验中多种压差工况下的压力梯度、空化分布、出口质量流量和截面流速分布进行数值模拟研究,对比讨论各模型组合之间的数值结果差异性,总结与评价模型选取对试验验证结果的影响。

1 计算模型理论

1.1 湍流模型

1.1.1 SSTk-ω模型

SSTk-ω模型由基线(BSL)k-ω模型改进而来,继承了k-ω类模型在近壁面区域中的鲁棒性、准确性,以及k-ε类模型在远场区域中的自由流独立性,并在湍流黏度中定义了湍流剪切应力的传输过程,其湍动能k和比耗散率ω的输运方程分别为

(1)

(2)

式中:ρ为流体密度;ui为流体速度在i方向上的分量,i为ijk空间坐标系的i方向;xi为流线分量x在i方向上的分量;Γk、Γω分别为湍动能k和比耗散率ω的有效扩散率;Gk为湍动能k的生成项;Yk、Yω分别为湍流引起的湍动能k和比耗散率ω的耗散项;Dω为交叉扩散项;Gb为浮力引起的湍动能;Gωb为ω输运方程中的浮力项。上述变量的具体表达式参见文献[11]。

1.1.2 Realizablek-ε模型

Realizablek-ε模型基于均方涡度波动传输方程导出了耗散率ε的修正传输方程,并且在多数流动中尤其是分离流和具有复杂特征的二次流中具有优异的计算性能,其湍动能k和耗散率ε的输运方程分别为

(3)

(4)

式中:μ为黏度;μt为湍流黏度;uj为流体速度在j方向上的分量,j为ijk空间坐标系的j方向;xj为流线分量x在j方向上的分量;YM为可压缩湍流流动中脉动膨胀对总耗散率的贡献程度;C1为方程中的一个系数项,

(5)

(6)

(7)

1.1.3 RNGk-ε模型

RNGk-ε模型在标准k-ε模型基础上使用重整化群的统计方法改进而来,该模型的特点在于提高了涡流计算的准确性,能有效计算近壁面区域的低雷诺数效应,因此RNGk-ε模型相较于标准k-ε模型的精度更高,适用的流动情况更广泛,其湍动能k和耗散率ε的输运方程分别为

(8)

(9)

式中:μeff为有效黏度;αk、αε分别为湍动能k和耗散率ε的有效普朗特数的倒数;C1ε、C2ε、C3ε为耗散率ε输运方程中的常数,C1ε=1.42、C2ε=1.68;Rε为耗散率ε输运方程的附加项。上述变量的具体表达式参见文献[13]。

1.2 空化模型

1.2.1 空化模型基本控制方程

空化模型可与控制气液混合物的多相流模型、传统的湍流模型一同构成多相流空化建模方法,其控制方程表述为

(10)

式中:fv为蒸气质量分数;vv为蒸气速度;Γ为扩散系数;Re为蒸气生成速率;Rc为蒸气凝结速率。

1.2.2 ZGB模型

ZGB模型假设多相流体系中的气泡都具有相同的大小,忽略不凝结气体对空化流的影响,并考虑使用单气泡质量变化率和气泡数密度来计算单位体积内的相间传质速率[14]:

当p≤pv时,

(11)

当p≥pv时,

(12)

式中:p为流场局部压力;pv为饱和蒸气压;Fv为蒸发系数,Fv=50;Fc为凝结系数,Fc=0.01;αn为气核处体积分数,αn=5×10-4;αv为蒸气体积分数;ρv、ρl分别为气相密度和液相密度;RB为气泡半径,RB=1×10-6m。

1.2.3 SS模型

SS模型使用气泡半径和气泡数密度来计算单位体积内的相间传质速率,忽略不凝结气体对空化流的影响,并假设当多相体系中没有气泡产生和湮灭时气泡数密度应保持恒定[15]:

当p≤pv时:

(13)

当p≥pv时:

(14)

式中:蒸发系数Fv=1;凝结系数Fc=0.2;α为气体体积分数。

2 数值模型构建及验证

2.1 物理模型构建

本文选取Winklhofer可视化燃油试验[5]中的U形管作为研究对象,其几何结构如图1[16]所示。 图1(a)展示了可视化试验使用的微通道组件,图1(b)是微通道的放大示意图。微通道模型几何参数如下:管道厚度W=300 μm,微通道入口高度Hi=301 μm,微通道出口高度Ho=284 μm,微通道长度L=1 000 μm,微通道入口拐角半径R=20 μm。

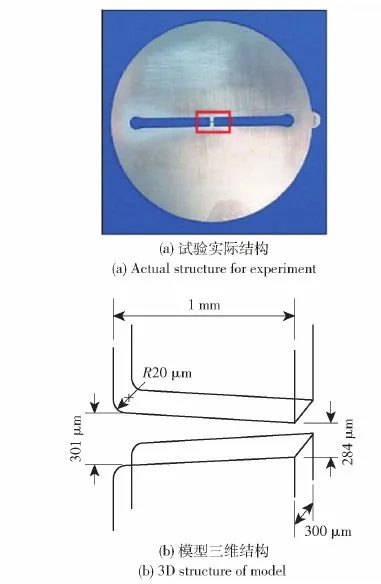
图1 微通道几何结构[16]Fig.1 Microchannel geometry[16]

在文献[8-9,17]中,使用额外预置缓冲流道的微通道模型与Winklhofer试验结果进行了对比验证,目的是为了让仿真时的微通道进出口压力与试验中的压力条件保持一致,以便仿真结果更接近实际试验测量结果。如图2所示,本文参考了 Guan等[17]的仿真模型,在微通道模型前后分别预置了2 000 μm×300 μm×2 312 μm和3 000 μm×300 μm×2 312 μm的缓冲流道。

图2 仿真计算模型Fig.2 Simulation calculation model

2.2 数值计算设置

数值计算时使用的燃油热物性参数如表1[17]所示,设置燃油为可压缩流体。此外,微通道进出口分别定义为压力入口条件和压力出口条件,保持100 bar的入口压力不变,为计算模型设置不同的出口压力条件(19～85 bar)。

表1 燃油热物性参数[17]Table 1 Fuel thermophysical properties[17]

数值模型的离散基于有限体积法,对于气-液两相流使用Mixture模型描述,压力-速度耦合方法使用压力隐式分裂算子(PISO)算法,压力求解格式和梯度求解格式分别设为PRESTO!格式、Least Squares Cell-Based格式,并将时间插值格式设置为2阶隐式格式以提高求解精度,其余格式设为QUICK格式。

2.3 网格无关性验证

对于微通道流域及微通道进出口附近的缓冲区流域,使用ICEM软件进行局部网格加密,以便后续的模型计算得到精确的流动参数结果,网格划分如图3所示。

图3 仿真模型网格分布Fig.3 Simulation mesh model

对于上述网格划分策略,依次采用量级为5万、20万、40万、60万、80万的网格进行网格无关性验证。在进出口压差为80 bar的工况下,Winklhofer流动试验已能观测到微通道中出现了超空化现象。因此,网格无关性验证基于上述压力工况,5种网格数下的微通道出口质量流量如图4所示。从图4中可见,当网格数量超过60万时,微通道出口处质量流量趋于一稳定值。考虑到后续数值计算的精度和计算资源分配,最终确定计算模型的网格数量为60万,其中近壁面处最小网格尺寸为0.5 μm,中央流道处最大网格尺寸约为4 μm。

图4 网格无关性验证Fig.4 Grid independence verification

3 计算结果和讨论

当前后缓冲区流域具有一定的压差,燃油流经微通道时,流道截面突然变小,流速突增,压力突降至燃油饱和蒸汽压力以下,此时会发生流动分离、空化等现象。上述现象直接影响了微通道流域的压力与速度分布,并反映在出口质量流量、空化区域分布、流速分布和压力梯度分布等结果参数上。本文分别研究以上物理参数的分布特性,对比分析多种数值模型应用情景下的结果差异,最终对可压缩燃油在多模型应用下的数值计算准确性进行讨论。

3.1 压力梯度结果对比

为了阐明通道内空化初生到空化发展的内在机理,首先结合Winklhofer等[4-5]试验数据,分析压差为70 bar情况下模型中心线处沿流向的压力梯度变化情况,如图5所示。其中,图5(a)中的x轴刻度对应图5(b)中的模型中心线标识。在该压力工况下,微通道内的燃油流动刚好达到临界空化条件。但由于此时的空化区域并未完全发展,燃油压力值先是在通道入口至空化区域中部迅速降低,并在局部流域横截面最小的空化区域中部降至极小值,然后流域横截面有所增加,压力值回升。在燃油液体流过空化区域末端并重新附着回壁面后,随着流体在不断接近通道出口的过程中,流域横截面逐渐减小,流速逐渐增加,导致压力也逐渐降低。

图5 压力梯度变化图Fig.5 Change in pressure

图5展示了多种湍流和空化模型应用下的压力梯度曲线变化差异。在燃油自上游缓冲区流域流至微通道入口附近,不同模型组合所得压力梯度曲线几乎重合,并与试验结果相近。随着燃油先后流经空化区域和无空化区域,除含有RNGk-ε模型的2种组合外,其余4种模型组合都有压力值先突降至一个极小值,再有所回升,最后逐渐减小的变化趋势。由表2可知:当模型中心线位置点处于 -1.00～-0.25 mm和-0.25～0.22 mm两个区段时,6种模型组合所得结果与试验数据接近,误差均在7%以内;处于0.22～0.50 mm和0.50～2.00 mm两个区段时,只有RNGk-ε+ZGB模型、RNGk-ε+SS模型这两种组合所得压力梯度平均值与试验数据相近,误差在6%以内。对于其他模型组合所得结果,其计算误差主要在10%～18%范围内,仿真效果较差。

表2 压力梯度平均值结果对比Table 2 Comparison of average pressure gradient results bar

3.2 空化分布结果对比

表3为试验和多种模型组合仿真的空化分布结果对比,其中Δp为前后缓冲区流域压差。由于前后缓冲区域存在压差,同时燃油在微通道中流动增加,使得局部区域的燃油压力降低至燃油蒸发压力,区域中的燃油瞬间蒸发为气相燃油,空化产生。

从表3中可以看出,不同模型组合所得的云图与试验结果之间存在明显的差异:由于实际燃油流动中存在着不凝结气体,导致燃油抗拉强度下降,燃油液体在压力下降过程中更容易产生气核,空化更容易发生[18]。同时,ZGB模型和SS模型皆未考虑不凝结气体对空化域的影响。表3中所示压差为60 bar工况下,6种模型组合都能模拟得到通道入口处的附着空化,与试验结果一致;压差为70 bar和80 bar工况下,6种模型组合所得空化域长度都比试验结果中的小。与试验结果对比可知,70 bar的压差工况下,6种模型组合模拟到的空化域长度远小于试验结果;80 bar工况下,SSTk-ω+ZGB模型组合所得空化域长度稍小于试验值,Realizablek-ε+ZGB模型组合所得结果与70 bar压差工况下的试验结果相当,其他4种模型组合所得空化域长度皆稍大于或相近于60 bar压差工况下的试验结果。

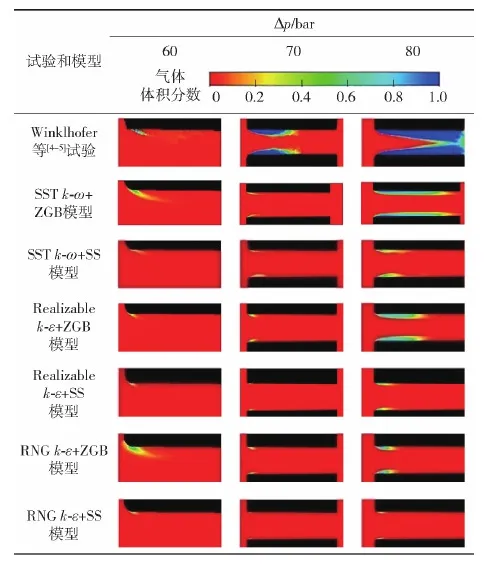
表3 气相体积分数云图

从试验结果可以看出,压差从60 bar增加至 80 bar,气相燃油不再局限于微通道入口处的回流区域,而是逐渐沿着壁面延伸至出口处。然而,试验中在微通道观察到的空化域比模拟所获取到的空化域大,不同空化模型所得到的空化分布情况也不同。Yu等[19]的研究结果表明,对同一微通道结构使用不同的空化模型,观测到的空化分布不同。 Giannadakis等[20]指出,空化域发展情况不依赖于空化泡初始直径。Altimira等[16]也发现试验中空化域比模拟中的大,并指出燃油压缩性会影响蒸气冷凝速率,这可能是造成模拟中的空化域偏小的原因。同时他进一步研究发现,使用不同密度的网格分布以及调节空化模型中影响空化泡发展的控制参数大小,对近壁面处的空化分布没有显著影响。

综上所述,随着进出口压差的增大,依附于微通道壁面的空化域不断发展,沿壁面逐渐延伸至通道出口处;在相同的进出口压差下,造成不同模型组合之间的空化分布差异性的原因是不同的湍流和空化模型在数学表述上存在差异。

3.3 出口质量流量结果对比

图6揭示了微通道出口质量流量与微通道进出口压差的变化特性,同时展示了6种模型组合所得模拟结果的差异。本文研究了13个压差工况下(Δp1=19 bar、Δp2=45 bar、Δp3=58 bar、Δp4=60 bar、Δp5=63 bar、Δp6=65 bar、Δp7=67 bar、Δp8=69 bar、Δp9=70 bar、Δp10=71 bar、Δp11=75 bar、Δp12=80 bar、Δp13=85 bar)的出口质量流量,与试验所采用的工况条件完全一致。

图6 出口质量流量图Fig.6 Outlet mass flow rate diagram

由试验结果可知,在压差从19 bar逐渐增加至85 bar的过程中,出口质量流量首先随着进出口压差的增大而增大,随后质量流量曲线在70 bar压差下出现拐点,在这之后的出口质量流量保持一定值,不再随压差的增大而变化。如图6所示,19～70 bar压差范围内,6种模型组合都能够获得与试验数据吻合较好的数值结果。表4为压力梯度平均值结果对比,由表4可知,将模型结果按试验数据划分成出口质量流量变化趋势不同的两个区段(19～70 bar和70～85 bar),6种模型所得结果与试验的平均值误差在10%以内。其中,Realizablek-ε+ZGB模型、RNGk-ε+ZGB模型两种组合的仿真误差较小,在两个区段内的误差均在4%以内。在 70 bar压差之后,Realizablek-ε+ZGB模型、RNGk-ε+ZGB模型2种组合计算到的结果虽然稍大于试验数据,但可以复现出口质量流量不再增加的趋势,其余4种模型组合模拟效果较差,无法反映出这一趋势。

3.4 流速结果对比

图7所示为55 bar和67 bar压差下微通道内2个横截面(x1=0.053 mm;x2=0.17 mm)沿y轴的速度分布情况。由于当压差为67 bar时,气化燃油完全占据了空化区域,试验过程中难以测量近壁面处的速度变化[5]。依照Winklhofer试验中截面流速分布的变化趋势,可将截面x1、x2在两种压差下的仿真结果分区段计算流速平均值,列表汇总,如表5～表8所示。

表4 压力梯度平均值结果对比Table 4 Comparison of average pressure gradient results g/s

在55 bar压差工况下,x1处的模拟结果可以反映出试验数据中的速度变化趋势,如图7(b)所示;图7(d)则表明在x2处所有模型组合均无法在远离微通道上下壁面约50～100 μm的范围内再现复杂的流速变化。由表5和表7可知,距离上下壁面约0～50 μm的近壁面流域内,仿真结果与试验数据仍有一定差距。在y轴位置点处于约50～250 μm范围内时(即截面x1、x2的中心流域),RNGk-ε+SS模型所得结果与试验数据最接近,即两处截面中的计算误差均在10%以内。SSTk-ω+ZGB模型的计算误差最大,在两处截面中的计算误差都超过了12%。

结合图7(c)和图7(e),在67 bar压差工况下,6种模型组合所得结果均与截面x1处试验数据的变化趋势吻合,但这仍难以在截面x2处复现远离壁面约50～100 μm范围内的流速分布。由表5和表7可知,相较于55 bar压差工况,67 bar压差工况下的近壁面流速分布的计算误差略有改善,但仿真结果与试验数据尚有一定差距。对于截面x1、x2的中心流域,RNGk-ε+SS模型的计算误差依旧最小,即两个截面处的计算误差均在6%以内。而SSTk-ω+ZGB的计算误差最大,在两处截面中的计算误差都超过了9%。

4 结论

本文分别使用SSTk-ω、Realizablek-ε和RNGk-ε湍流模型以及ZGB和SS空化模型,对不同进出口压差工况下的Winklhofer微通道试验模型中的空化现象进行了数值计算研究。得到主要结论如下:

1)在压差为70 bar时,虽然RNGk-ε+ZGB模型、RNGk-ε+SS模型相较于其余4种模型组合,反映出微通道中心线处沿流向的压力先突降至一个极小值,再有所回升,最后逐渐减小的变化趋势的效果较差,但RNGk-ε+ZGB模型、RNGk-ε+SS模型这两种组合所得压力梯度平均值与试验数据较相近。总体上看,上述两种模型组合的计算误差都在7%以内。在相同的压差工况下,模拟所得空化域长度小于试验观测所得的空化域长度。不同模型组合之间的空化分布存在差异性,原因是不同的湍流和空化模型在数学表述上存在着差异。

2)出口质量流量的数值计算方面,6种模型组合均可在19～70 bar的压差范围内计算得到与试验数据吻合较好的数值结果,计算误差控制在10%以内。在压差超过70 bar后,只有Realizablek-ε+ZGB模型、RNGk-ε+ZGB模型2种组合的计算结果仍然可以反映试验数据的变化趋势,且计算误差在4%以下,而其余4种模型组合均无法体现出实际测量下的出口质量流量变化情况。

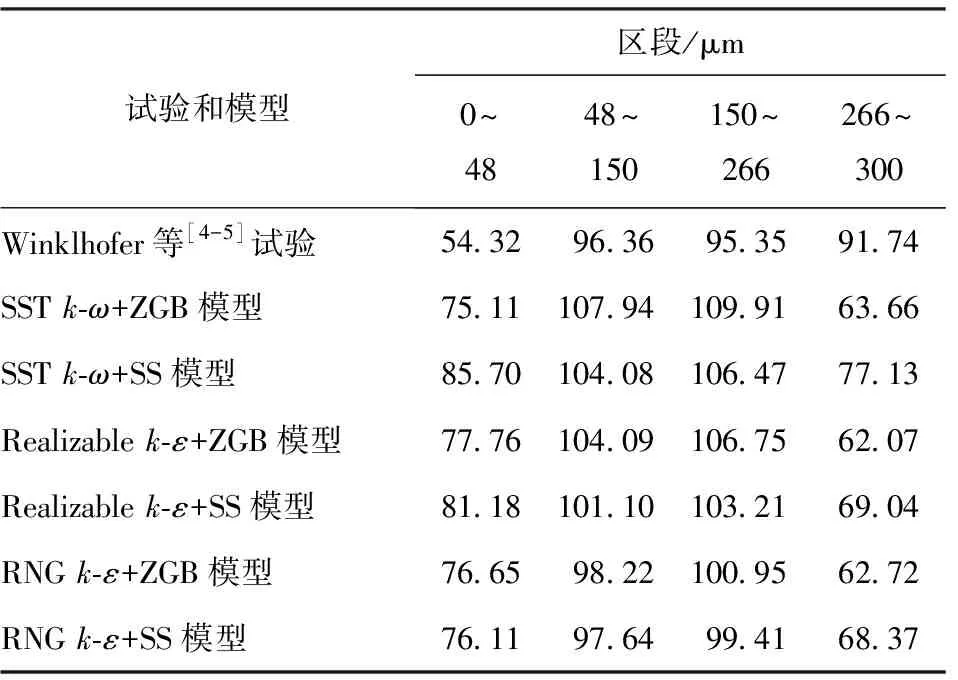
表5 55 bar压差下截面x1流速平均值结果对比Table 5 Comparison of average flow rate results of sectionx1 at 55 bar differential pressure m/s

表6 67 bar压差下截面x1流速平均值结果对比Table 6 Comparison of average flow rate results of sectionx1 at 67 bar differential pressure m/s

表7 55 bar压差下截面x2流速平均值结果对比Table 7 Comparison of average flow rate results of sectionx2 at 55 bar differential pressure m/s

3)沿y轴的流速分布数值计算方面,在距离上下壁面约0～50 μm的近壁面流域内,6种模型组合仿真所得结果与试验数据仍有一定差距。在截面x1、x2的中心流域内,RNGk-ε+SS模型的计算结果变化趋势与试验数据最吻合,并且55 bar和 67 bar 两种压差工况下的计算误差分别在10%以下和6%以下。SSTk-ω+ZGB模型组合的计算误差最大,两种压差工况下的计算误差分别超过12%和9%。>

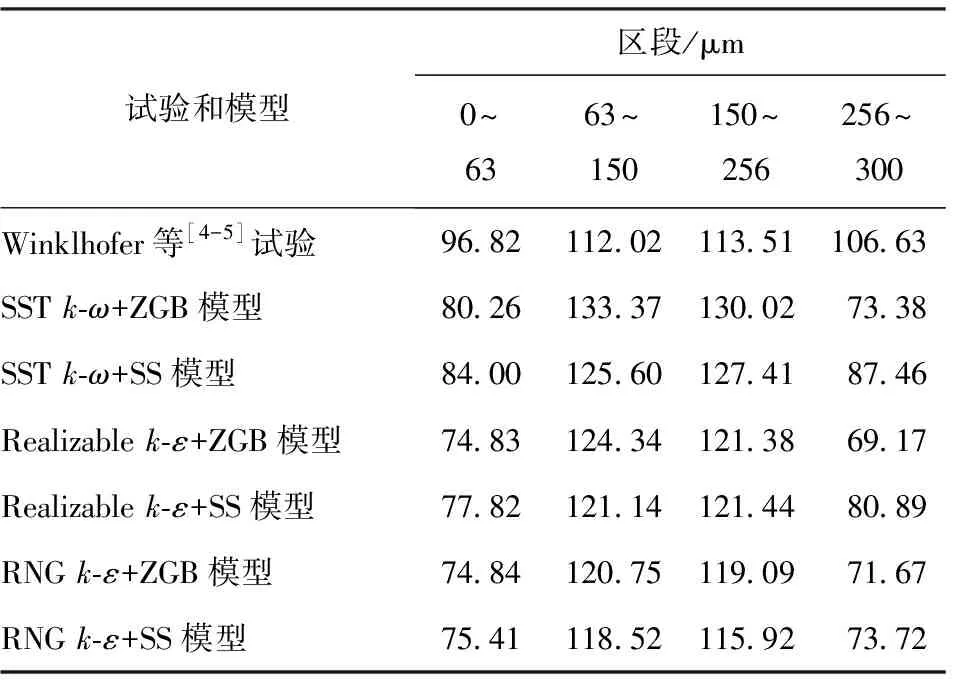
表8 67 bar压差下截面x2流速平均值结果对比Table 8 Comparison of average flow rate results of sectionx2 at 67 bar differential pressure m/s

4)与Winklhofer试验数据对比,RNGk-ε+ZGB模型、RNGk-ε+SS模型适用于计算微通道中心线处的压力梯度变化;6种模型组合未能较好地反映处试验时的空化分布情况;Realizablek-ε+ZGB模型、RNGk-ε+ZGB模型可用于计算喷油器微通道的出口质量流量情况;RNGk-ε+SS模型则可以用于计算微通道在发生空化时的某一截面的流速分布情况。