基于多项分布的弹药多批次试验命中概率估计

刘昊邦, 史宪铭, 郝冰, 姜永超

(陆军工程大学石家庄校区 装备指挥与管理系, 河北 石家庄 050003)

0 引言

弹药命中概率试验通常包含多个批次,并在每批次试验结束后对弹药物理性能进行改进,弹药命中概率随批次逐渐提高[1]。各批次试验数据服从总体不同,因此考虑多批次试验命中概率估计问题尤为必要。

现有弹药命中概率研究主要考虑单批次试验,即只利用一个批次弹药射击试验数据,试验数据服从同一总体。单批次弹药命中概率估计方法主要包括蒙特卡洛模拟法、射弹散布分析法、二项分布成败型数据法等。Trzun等[2]基于蒙特卡洛方法分析单发火箭弹射击误差情况,计算出了火箭弹命中概率。Corriveau等[3]研究了不同射击位置和不同射击场景对武器命中概率的影响。Khaikov[4]考虑目标类型和瞄准点因素,研究了弹药命中概率随水平距离的变化情况。王保华等[5]根据高炮预制破片弹对空中目标的毁伤机理建立毁伤能力模型,对火箭防空武器的命中概率进行了计算。Seo等[6]对精确制导导弹命中概率和置信水平估计进行了研究。Kang等[7]对防空火炮命中概率进行了预测。上述研究未能考虑弹药多批次试验特点,无法科学、合理地利用各批次试验信息,且这些研究仍以命中与否的成败型数据为研究基础,结果较为粗泛、适应性差。

充分利用各批次试验信息,是解决弹药多批次试验命中概率估计问题的关键。贝叶斯方法在信息融合领域应用较为广泛,考虑运用贝叶斯方法对各批次试验信息进行融合。Li等[8]基于贝叶斯方法融合专家信息和仿真信息,对弹药消耗进行了预计。Guo等[9]利用贝叶斯信息融合方法对退化数据产品的可靠性进行了分析。Papananias等[10]基于机器学习贝叶斯信息融合方法进行了终端产品质量评估。上述研究为贝叶斯方法信息融合提供了借鉴。在融合过程中注意到,距离最终批次试验越近的信息更能发挥主导作用,因此需要对不同批次信息的融合权重进行确定。体系贡献度常用于衡量武器装备对作战体系作战能力的贡献程度[11],通过引入体系贡献度可以计算不同批次信息权重。

此外,仅利用成败型数据的二项分布法,在样本数量较少时难以对弹药命中概率进行估计。考虑弹药落点分布的射弹散布分析法虽然利用信息更为全面,但仅适用于射弹散布有规律可寻的情况,对射弹散布规律不明显的弹药并不适用。为更细致地描述弹药命中概率,从弹药打击目标的实际出发,弹药打击目标会命中目标不同区域,造成目标毁伤效果不同,命中各区域都有一定概率发生。为了对二项分布法进行改进,可以改用多项分布描述弹药命中概率试验。

综合以上分析,本文采用贝叶斯方法融合各批次试验信息,并利用体系贡献度确定信息融合权重。同时对原有基于成败型数据的二项分布法进行改进,改用多项分布进行试验描述。最终提出基于多项分布的弹药多批次试验命中概率估计方法。

1 多项分布弹药命中概率试验

现有弹药命中概率试验主要从命中成败的二项分布角度进行分析。即假设命中概率为P,共发射n发弹药,命中概率试验[12]可表示为

(1)

式中:x为命中目标的弹药数。

二项分布贝叶斯方法通常选择弹药命中概率参数P的共轭分布Beta分布作为先验分布:

(2)

式中:先验分布包含参数P的先验信息;a、b为先验分布中的超参数。

二项分布适用于两级毁伤目标情况,即弹药命中目标可使目标功能完全丧失。对于多级毁伤目标,弹药在试验中命中目标不同区域造成的毁伤程度不同。此时按照弹药打击造成的毁伤程度,可将目标区域划分为无毁伤区域、轻度毁伤区域、中度毁伤区域、重度毁伤区域[13]。弹药命中无毁伤区域未能造成目标损伤,命中重度毁伤区域能够完全摧毁目标。弹药命中概率试验会产生4种命中结果,分别为命中无毁伤区域、轻度毁伤区域、中度毁伤区域、重度毁伤区域。每种结果都有一定概率发生,记为Pi,i=1,2,3,4。在n发弹药试验中,采用多项分布描述弹药命中概率试验[14]可表示为

(3)

贝叶斯先验分布选择方法包括无信息先验分布法、最大熵法、共轭先验分布法等。无信息先验分布法适用于先验信息不够充分的情况[15],而本文拥有各批次试验信息。最大熵法计算过程复杂,不易求解[16]。因此选择共轭先验分布法确定先验分布。查阅贝叶斯相关文献可知多项分布的共轭分布为Dirichlet分布[17],可表示为

(4)

式中:αi为先验分布中的超参数;Γ(αi)为Gamma函数。

采用多项分布描述命中概率试验,能够获取弹药命中目标不同毁伤区域的概率。相比仅利用命中成败数据的二项分布方法,采用多项分布描述弹药命中概率试验更为合理。

2 基于体系贡献度的多批次试验信息融合

多批次弹药命中概率试验包含多个批次试验信息。距离最终批次试验越近的信息价值越高,对弹药命中概率估计贡献程度越大。因此在信息融合过程中亟需确定各批次试验信息的贡献程度。

2.1 多批次命中概率试验信息融合过程

多批次命中概率试验信息来源主要包括射击试验信息、前一批次弹药命中概率信息、仿真实验信息[18]。信息融合过程如图1所示。

距离最终批次越近的信息更能在弹药命中概率估计中占据主导地位,因此需要衡量不同信息在最终批次弹药命中概率估计中的贡献程度。

2.2 基于体系贡献度的融合权重计算

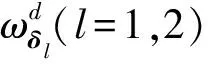
(5)

在采用直觉模糊隶属函数法确定弹药命中概率信息隶属度过程中,注意到专家看待弹药命中概率信息来源是否可靠时会犹豫,引入直觉指标表示专家犹豫程度[22],表达式为

(6)

确定先验信息权重中采用犹豫程度的一半进行修正,可以求出信息δl的隶属度表达式如下:

(7)

进行归一化处理,可以得到信息δl的融合权重:

(8)

(9)

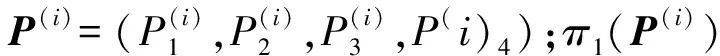
3 弹药多批次试验命中概率贝叶斯推断

与单批次试验研究不同,多批次试验需要考虑每一批次信息,从初始批次开始对各批次试验命中概率进行分析。

3.1 初始批次命中概率贝叶斯推断

初始批次弹药命中概率估计只包含初始批次射击试验信息L(x(1)|P(1))和仿真实验信息π(P(1)|α(1))。利用贝叶斯方法将上述信息进行融合可以求出初始批次弹药命中概率分布:

(10)

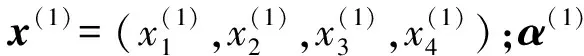
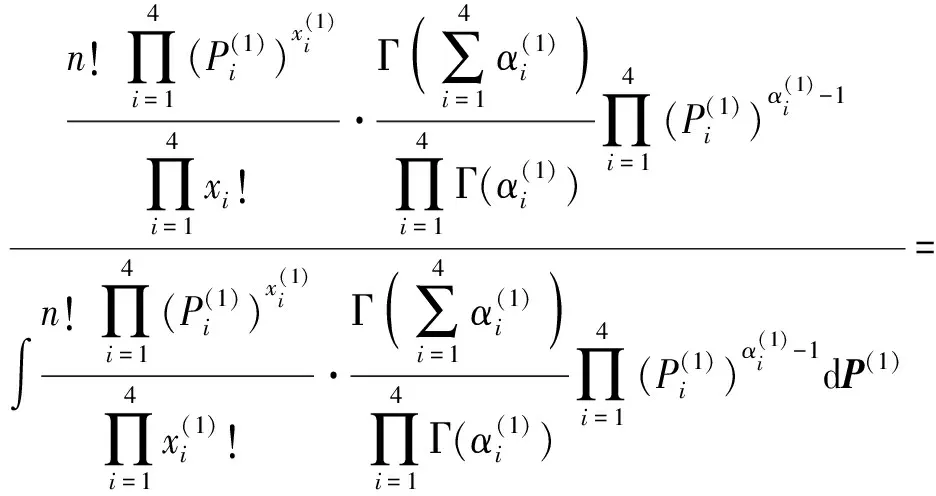
(11)

(12)

初始批次结果可作为第2批次先验信息进行使用。

3.2 第2批次命中概率贝叶斯推断

经过初始批次试验之后对弹药物理性能进行改进,并进行第2批次试验。第2批次试验在估计弹药命中概率时需要将初始批次试验信息考虑进去。因此第2批次试验包含信息有第2批次射击试验信息L(x(2)|P(2))、第2批次仿真实验信息π(P(2)|α(2))、初始批次弹药命中概率信息π(P(1)|x(1))。相比初始批次试验,第2批次试验信息增加了初始批次试验信息。依据第2节提出的体系贡献度确定信息融合权重,并利用贝叶斯方法求得第2批次弹药命中概率分布:

(13)

3.3 第i批次命中概率贝叶斯推断

同理,第i批次试验包含信息有第i批次射击试验信息L(x(i)|P(i))、第i-1批次弹药命中概率信息π(P(i-1)|x(i-1))、第i批次仿真实验信息π(P(i)|α(i))。 其中π(P(i-)|x(i-1))包含从初始批次至第i-1批次命中概率所有信息。第i批次弹药命中概率用贝叶斯公式表示为

(14)

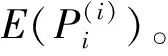
(15)

上述顺序约束关系分别表示第i批次弹药命中轻度及以上毁伤区域、中度及以上毁伤区域、重度毁伤区域的概率大于第i-1批次,表明对弹药命中性能进行了改进。

4 马尔可夫链-蒙特卡洛方法多批次试验命中概率求解

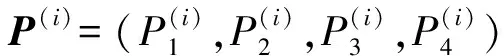
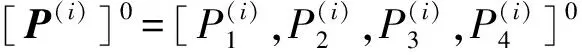
3) 继续进行迭代转移,产生新的命中概率参数点序列[P(i)](k+1),[P(i)](k+2),…,[P(i)](m)。

4) 去除掉马尔可夫链收敛状态之前的k个点序列,选用新的点序列作为命中概率参数P(i)的抽样值,可以求出命中概率参数P(i)的后验期望:

(16)

由于命中概率参数P(i)维数较高,不易直接抽取样本,此时需要借助Gibbs抽样方法将高维样本转化为每次只抽取一个参数的一维抽样问题,从而便于抽样实现。

基于Gibbs抽样方法步骤[24]如下:

1) 确定命中概率参数后验分布的一元条件分布,从一元条件分布中抽样比直接从多元后验分布中抽样容易很多。依据命中概率参数后验分布公式可以求出后验一元条件分布:

(17)

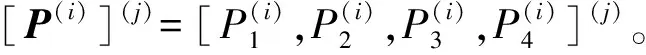
3) 选择马尔可夫链平稳状态时段的点序列均值作为弹药命中概率参数贝叶斯估计值:

(18)

根据抽样结果若发现不满足约束关系,即出现第i批次弹药命中概率小于第i-1批次情况,表明该批次试验之前对弹药命中性能改进不理想,需要进一步对弹药命中性能进行研究。

5 示例分析

为测算某型号弹药命中概率,共进行3个批次射击试验,每批次发射10发弹药。每次射击试验之后对弹药命中性能进行改进,弹药命中概率认定逐步提升。获取这3个批次射击试验信息以及仿真实验信息,结果如表1所示。

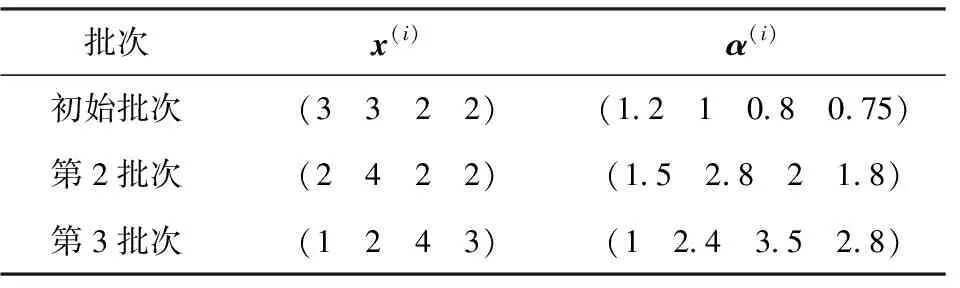
表1 多批次试验弹药命中概率信息Table 1 Ammunition hit probabilities in multiple-batch tests

按照体系贡献度打分规则,邀请6位同领域专家对第i-1批次弹药命中概率信息δ1和第i批次仿真实验信息δ2的隶属度进行打分。打分结果如表2所示。

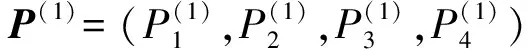
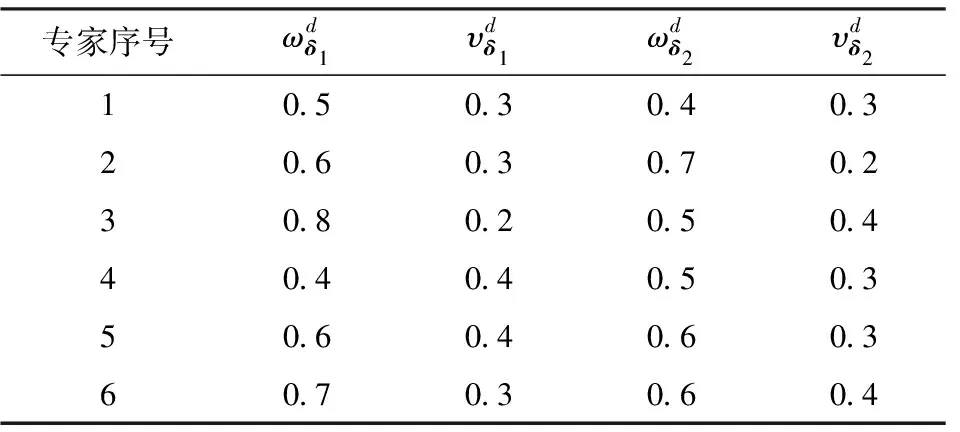
表2 先验信息专家隶属度打分Table 2 Prior information membership score in expert interview

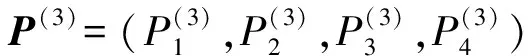
生成各批次弹药命中概率参数概率密度函数图,如图5所示。对各批次参数马尔可夫链结果进行统计,如表3所示。

表3中贝叶斯统计结果给出各批次试验命中概率参数的均值和方差。以第3批次试验作为最终批次,可以得到最终批次弹药命中无毁伤区域概率的均值为0.124、方差为0.084 7;轻度毁伤区域概率的均值为0.251、方差为0.199 3;中度毁伤区域概率的均值为0.343、方差为0.244 3;重度毁伤区域概率的均值为0.282、方差为0.212 3。从结果中可以看出,本文方法能够得出弹药命中目标不同毁伤区域的概率分布情况,相比依据命中与否的二项分布方法,所得概率更为全面。同时发现各批次结果满足顺序约束关系,表明每批次试验之后对弹药命中性能进行了有效改进。

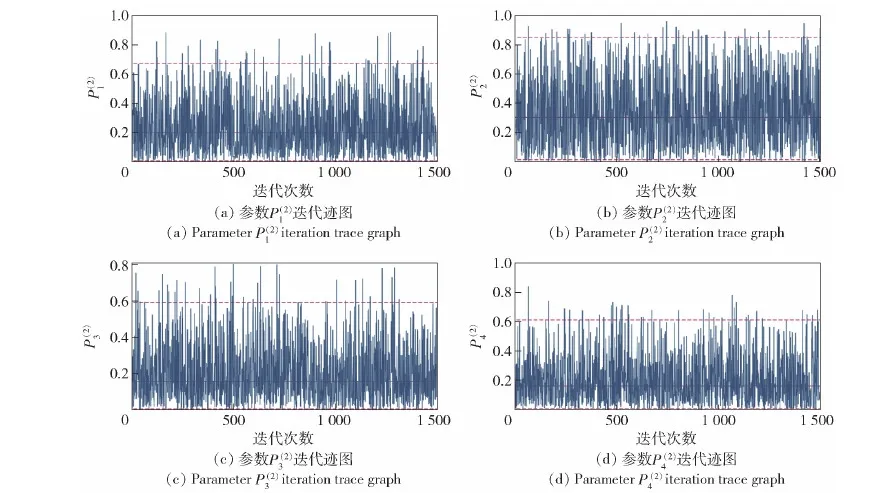
图3 第2批次命中概率参数迭代迹图Fig.3 Iteration trace graph of the second-batch hit probability parameters

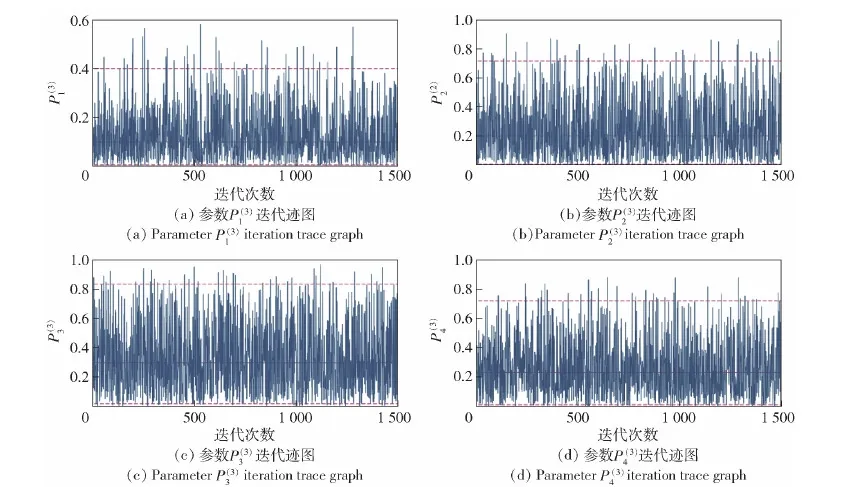
图4 第3批次命中概率参数迭代迹图Fig.4 Iteration trace graph of the third-batch hit probability parameters

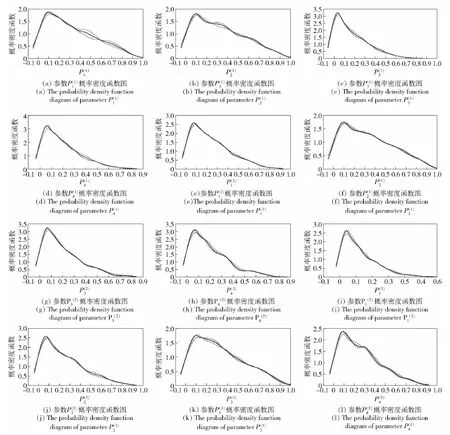
图5 各批次弹药命中概率参数概率密度函数图Fig.5 Probability density function diagram of ammunition hit probability parameters of each batch

6 结论

本文对基于多项分布的弹药多批次试验命中概率估计进行了研究,在现有二项分布、单批次试验研究的基础上,从实际试验过程出发对多项分布、多批次试验弹药命中概率进行估计。得到如下主要结论:

表3 各批次弹药命中概率参数贝叶斯统计分析Table 3 Bayesian statistical analysis of ammunition hit probability parameters for each batch

1) 考虑弹药命中概率试验通常分多个批次进行的实际情况,在进行多批次命中概率估计时,通过体系贡献度确定各批次试验信息的融合权重。

2) 采用贝叶斯方法对各批次射击试验信息与仿真实验信息进行融合,从而实现融合各批次试验信息的目的。

3) 考虑弹药命中目标不同毁伤区域的实际情况,以弹药命中目标不同毁伤区域的概率作为弹药命中性能指标,采用多项分布描述命中概率试验,能够细致描述弹药命中性能,为弹药命中概率估计提供借鉴。