基于迁移学习的供药装置故障诊断方法

黄文宽, 钱林方,2*, 尹强, 刘太素

(1.南京理工大学 机械工程学院, 江苏 南京 210094; 2.西北机电工程研究所, 陕西 咸阳 712099;3.南京工程学院, 江苏 南京 211167)

0 引言

模块装药[1]是新一代大口径火炮实现自动化的基础,通过模块药供药装置可以实现对模块发射药的储药、选药和供药,以此在装填时可以方便的变换装药量,进一步实现火炮在同一射角下不同射程的击发。模块供药装置是大口径火炮供输药系统的起点和重要一环,当它发生故障时,火炮射速将受到大幅影响。严重的供药装置故障可能会引发事故,毁伤己方装备和人员。随着火炮自动化水平的提高,为保障供药装置的正常运行,有必要对其进行智能化故障诊断的研究[2]。

近年来,许多传统机器学习方法被广泛应用于各类机械装置的故障诊断中。文献[3-4]将人工神经网络、K最邻近法、随机森林和支持向量机(SVM)等机器学习方法应用到轴承的故障诊断问题上,区分出轴承的各类异常振动数据。文献[5-6]侧重于对时域信号的分析,将小波分析、经验模态分解、奇异值分解(SVD)等方法应用于故障特征的提取。文献[7]将多种深度神经网络方法应用于轴承的故障诊断,实现了从原始信号到故障分类的端到端分析。至此,通过时域分析提取目标信号的特征再结合机器学习算法进行分类识别的故障诊断方法趋于成熟。上述故障诊断方法尚存在不足,首先,所采用的传统机器学习方法需要大量分布均衡的训练数据。其次,研究对象往往以轴承等高故障率零部件为主,对火炮系统供药装置的故障诊断研究几乎处于空白状态。

供药装置的结构复杂、工况多样,其故障具有复杂性、多样性、隐蔽性[8-9]等特点;供药装置作为大口径火炮的子系统,还具有故障率低、试验成本高等特点。这使得在供药装置上直接通过试验获得一个数据量充足且各类故障样本分布平衡的数据集是十分困难的,进而导致传统机器学习方法在解决供药装置故障诊断问题时受到制约。

为解决训练样本不足带来的问题,文献[10]在梳理并展望智能故障诊断的理论发展时,提出可以借助迁移学习方法。迁移学习可以利用数据、任务或者模型之间的相似性,利用旧有知识帮助目标任务进行训练。TrAdaBoost算法[11]作为一种典型的迁移算法,通过大量旧有数据辅助少量全新数据即可学习一个适用于新数据的精确模型,已在工程实际中取得了广泛应用。Chen等[12]将TrAdaBoost算法应用到风电机组的故障诊断中,解决不同外部环境下风电机组故障数据不平衡的问题。Shen等[13]利用西储大学电机轴承数据中心的公开实验数据,对变转速变负载条件下的电机轴承进行了故障诊断。Xiao等[14]运用TrAdaBoost算法,针对几台故障样本量较小的电机进行了高精度的故障诊断。可见,TrAdaBoost算法在处理多工况、少样本且数据分布不平衡的故障诊断问题时,具有优越的性能。

本文在已有研究的基础上,基于迁移学习方法对传统的时域分析-分类器模式加以改进,应用到供药装置的故障诊断上。首先用机械系统动力学自动分析软件建立供药装置的仿真模型,生成考虑实际工况噪声影响的仿真样本,用以辅助试验样本进行迁移学习训练;其次利用自相关矩阵-SVD的方法提取出仿真样本与试验样本的特征向量并组成训练集,根据两类特征向量的相似度对每个训练样本权重进行初始化,最后在TrAdaBoost算法框架下,迭代训练出一些加权支持向量机(WSVM)并集成出一个可以对供药装置进行故障诊断的高性能分类器,实现对供药装置高效且精准的故障诊断。

1 供药装置的故障模式分析

1.1 供药装置的结构与仿真模型

供药装置是集机电液控为一体的复杂系统,在各子系统的协同工作下,它能自动化得实现对模块药的储药、选药以及供药功能。供药指令发出后,电机在控制信号的驱动下,通过减速器将驱动力矩传递到供药链轮上进而带动供药链条将指令需求数量的模块药推入装填装置。在储药筒的前后端都安装有阻尼块,保证模块药不会意外掉落,同时确保模块药始终在与供药链头的贴合下保持强制运动。供药装置的结构如图1所示。

图1 模块药供药装置示意图Fig.1 Schematic of modular charge feeding mechanism

在动力学仿真软件中对上述结构进一步简化,仅保留供药链条(包括滚轮、销轴、链节等细节)、储药筒以及阻尼块等结构,电机的驱动力矩也以仿真力矩的形式添加在供药链轮上。建模过程在文献[15]中进行了介绍,仿真模型如图2所示。

图2 模块药供药装置仿真模型Fig.2 Simulation model of modular charge feeding mechanism

1.2 供药装置的典型故障

在供药装置的实际使用过程和可靠性试验中可以发现,供药装置的故障类型大致可分为机械故障、电气控制系统故障和液压系统故障三类。其中电气控制系统故障和液压系统故障的故障特征容易通过各自系统内的传感器或算法直接检测。而机械故障则因为故障种类繁多、无合适的传感器安装位置等原因,需要借助机器学习的方法,从单一的目标信号中甄别出多种机械故障类型。

常见且影响较大的机械故障主要来源为零部件的加工装配问题和磨损问题。如图3所示,这类故障的故障率和供药装置的使用时间呈现明显的浴盆曲线关系,在一个可靠性试验周期内,具体一种零部件发生的机械故障次数非常有限,且类型之间呈现明显的分布不平衡。图3中,T1为规定的装配调试工作次数,T2为满足可靠性指标的无故障次数。

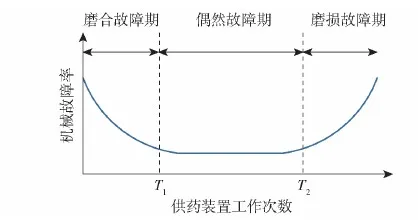
图3 供药装置机械故障曲线Fig.3 Mechanical failure curve of modular charge feeding mechanism

供药装置的一个重大电气控制系统故障是选药数量出错。该问题将导致火炮实际射程与作战需求不符,进而造成打击效果不佳甚至毁伤己方目标的严重后果。为防止相关电气元件在使用中失效,也应使用机器学习方法从其他目标信号对供药装置选药数量进行监测,作为一种多源故障诊断方案。

综合上述分析与火炮实际使用过程中的情况,本文选择以选药数-故障类型的组合作为供药装置故障诊断分类问题研究的典型对象。

选择3种典型的供药装置选药数量:

1)1块模块药;

2)4块模块药;

3)6块模块药。

3种选药数量分别代表火炮实际使用中的最小装药量、常用装药量和最大装药量。

选择3种典型的供药装置故障状态:

1)阻尼块磨损失效;

2)储药筒碰撞变形;

3)供药装置健康完好。

其中阻尼块作为短寿命件,易因不及时更换而随着使用次数增加逐渐磨损失效。储药筒虽然寿命较长,但是在装配过程和火炮实际使用过程中也曾发现其受到外力冲击产生塑性形变进而发生故障。

综上产生9种选药数-故障类型作为典型组合,各组合在900次的可靠性试验周期中被记录到的分布占比以及缩略表述如表1所示。

表1 选药块数与故障情况的组合Table 1 Combinations of modular charge numbers and faults conditions

2 基于迁移学习的故障诊断方法设计

2.1 目标信号分析

理想状态下供药装置中模块药与供药链头在贴合状态下共同位移,故可用供药链头的位移速度曲线近似表达模块药的位移速度状态。当供药装置实际发生影响功能的故障时,供药链头的位移速度曲线相较正常曲线会发生变形或偏移。

试验中,通过安装在供药链轮上的光电编码器获得供药链头的位移速度信号,将之作为供药装置故障诊断研究的目标信号。这是混杂了噪声的采样周期固定的离散信号

(1)

供药装置的实际使用工况恶劣,战场环境以及自身火炮工作时均包含巨大噪声,因此光电编码器中混入的干扰噪声不能忽略。本文讨论的干扰噪声N是台架试验中混入的噪声,旨在测试本方法对含噪声样本的适应性,提升分类器的性能和鲁棒性[16]。

确定目标信号后,为后续使用迁移学习策略,利用仿真方法生成大量与试验样本近似的仿真样本用以辅助分类器的训练。类似有

sim=ssim+Nsim

(2)

仿真速度信号ssim可在动力学自动分析软件中使用采样周期T对供药装置的工作过程进行仿真和采样直接得到,模拟噪声Nsim则要先对真实干扰噪声进行分析。

在台架试验统计了足够长时间的干扰噪声后,计算此噪声的概率密度函数和功率谱密度,如图4所示,干扰噪声的概率密度函数服从高斯概率分布,而功率谱密度在高频段服从均匀分布,可以看作一个高斯白噪声与数个固定低频的噪声的叠加。

图4 干扰噪声的功率谱密度和概率密度函数Fig.4 Power spectral density and probability density function of noise

维纳-辛钦定理表明随机信号的功率谱和其自相关函数是一对傅里叶变换,在统计时间足够时,干扰噪声的功率密度谱是相对固定的。仿真干扰噪声Nsim可以是一段符合干扰噪声N功率密度谱的随机信号,可由式(3)和式(4)得到

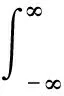
(3)

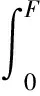
(4)

式中:Px(f)和Rx(τ)分别为干扰噪声N的功率谱密度和自相关函数,f为功率谱密度函数上的频域,τ为自相关函数上的时域,函数下标x表示单边频谱;Pxx为与功率谱密度Px(f)共轭对称的双边功率谱密度;σ2为所构造噪声的方差。

图5(a)为3条典型试验样本的供药链头速度曲线的对比,图5(b)为一条健康试验样本的供药链头速度曲线与同类仿真曲线的对比,并展示了供药链头在工作过程中大致可以分为的4个阶段(见图5(b)中阶段1～阶段4):1)与模块药接触碰撞阶段;2)与模块药贴合克服阻尼块阻力加速阶段;3)平稳供药位移阶段;4)供药结束复位阶段。

图5 典型试验样本和仿真样本速度曲线Fig.5 Velocity curves of typical simulation and test samples

通过分析图5(b)可知,阶段1波形尖锐,是由供药链头空载加速后与模块药接触碰撞所产生的,与本文研究的典型故障问题关系不大。阶段2的平均斜率一定程度反映阻尼块对模块药的阻力变化。阶段3可以找到一些周期性的故障特征,利用自相关函数可以很好地将此类周期性问题放大。阶段4为供药链条空载复位过程,可以不纳入考虑。

2.2 基于SVD的特征向量提取

SVD与汉克尔矩阵结合使用可实现一维时间序列数据的降维和降噪。对于式(1)中某一个离散信号样本x(t),它所对应的自相关函数为

c(j)=E(x(t)x(t+j))

(5)

构建关于它的自相关函数的汉克尔矩阵如下:

(6)

式中:M和N为与样本适应的合适维数。

对式(6)进行SVD:

(7)

ΣM×N=diag[σ1,σ2,…,σQ]

(8)

式中:UM×N为左奇异向量组成的矩阵;ΣM×N为奇异值组成的矩阵;VM×N为右奇异向量组成的矩阵;σ1,σ2,…,σQ为矩阵H分解后的奇异值,Q=min {M,N}。

奇异值代表原矩阵在两个标准正交基之间对应向量的比例关系,可以用奇异值组成的奇异值向量x=(σ1,σ2,…,σQ)代表原矩阵所包含的信息,达到了对数据降维的效果。奇异值由大到小排列且衰减速度极快,最大的几个奇异值一定程度反映矩阵内部信息的冗余程度,可以省略较小的奇异值来去除冗余信息,达到降噪的结果。

定义‖A‖2,2=sup‖Au‖2/‖u‖2,u为矩阵A的任意一个列向量。

令Σn=diag[σ1,σ2,…,σn,0,…,0],通过其复原的矩阵Hn=UΣnVT,存在‖H-Hn‖2,2=σn+1的关系。文献[17]给出了推导过程,保证了用SVD方法对数据进行降维和降噪处理是可控的。

图6为通过式(5)～式(8)对一些典型样本进行SVD后得到的奇异值向量。

图6 典型样本奇异值向量的对数曲线Fig.6 Logarithmic curves of singular value vectors of typical samples

由图6可以看出,奇异值曲线前段部分区分度明显,后段部分则重叠严重且数值较小,根据本节上文结论可以逐步从后段截去冗余部分,以寻找合适维度的奇异值向量作为特征向量。假设经过截取后,奇异值向量剩余k个值,则此时最小的奇异值为σk,定义此时的任意两个特征向量xi和xj之间的区分度为

(9)

Dk恰好满足时,特征包含信息量、分类性能和诊断计算量,三者可以得到比较好的平衡。

2.3 Boosting风格的迁移学习方法

集成学习的根本思想是将多个性能不佳的弱分类器用策略结合起来共同完成同一个任务。可视作基于若干弱分类器,构造一个强分类器。Freund等[18]提出的AdaBoost是一种Boosting风格的集成学习算法:先从初始训练集中训练一个基学习器,根据其性能表现来对训练样本的权重和分布进行调整,而后训练一个新的基分类器;如此反复直到训练出足够多的符合预期效果的基分类器,最终选择若干个性能较优的基分类器进行加权结合,得到一个集成强分类器。

Dai等[11]提出的TrAdaBoost算法的目标是在推广的AdaBoost算法的基础上,应用迁移学习的思想,实现对少量目标数据的分类,属于一种归纳式迁移学习方法。本文方法在TrAdaBoost的框架下对供药装置的几种选药数-故障组合的特征向量进行识别。

设所有用于训练的特征向量组成的集合为D,

(10)

式中:Ds表示由仿真样本特征向量组成的训练集,称为仿真集;Dt代表由试验样本特征向量组成的训练集,称为试验集;xs,i和ys,i为仿真集Ds的第i个特征向量和对应的类别标签;xt,i和yt,i为试验集Dt的第i个特征向量样本和对应的类别标签,标签按表1的规定人工标注;ns和nt为仿真集和试验集的样本数量,且ns≫nt。

本文方法采用重加权策略,首先利用大量仿真集训练样本与少量试验集训练样本联合训练一个基分类器,随后主要考察该基分类器对于试验集样本的分类效果。该方法建立一种偏心的自动调整权重的机制,对于造成损失较大的仿真集样本,认定其不利于目标任务,在下一次迭代中降低权重,而对于造成损失较大的试验集样本则会在下一次迭代中增加权重以求更好的拟合效果。通过以上方法,最终联合有利目标任务的仿真集样本和试验集样本训练出多个基分类器,最终为目标任务集成学习一个强分类器。算法流程和步骤如下:

1)在联合训练集D中,统计属于Ds和Dt的样本个数n和m,设置最大迭代次数Ite。

以该权重结合训练集D训练WSVM作为基分类器ht,t代表当前训练迭代轮次,t=1,2,3,…,Ite。

4)统计ht在Dt上的平均损失εt,其中l(·,·)为损失函数:

(11)

5)设置权重更新参数:

(12)

且当εt≥1/2时算法早停。

6)根据样本来源更新对应的权重:

(13)

7)利用后半部分的基分类器进行投票,最终得到集成分类器H:

若有

(14)

则输出H(x)=y,y为算法对样本的最终分类。

2.4 可迁移度与负迁移

用于训练目标任务的两个训练集相似度过低,或者基本不相似,将使得目标任务无法完成,这种现象称之为负迁移[19]。假设本文方法中,在引入仿真集后无论如何使用重加权策略,都不能对目标任务起到积极作用,就可以认为发生了负迁移。

文献[20]给出了负迁移的数学定义,并提出负迁移间隙NTG来确定负迁移是否发生:

NTG=ε(θ(Ds,Dt))-ε(θ(∅,Dt))

(15)

式中:ε表示目标任务中的测试错误率;θ(·)表示采用的迁移学习算法。

按表1规则,将9种选药数-故障类型组合标识为id(id=1,2,3,…,9),ps,id和pt,id分别表示每个id的组合在Ds和Dt中的边缘分布,即每种组合在各自训练集中的占比。

定义可迁移度作为两者共性的量化标准,并对组合标识为id的样本进行相似度量化,步骤如下:

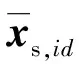
2)计算第id类故障特征向量相似度:

(16)

综合第id类故障组合的奇异值向量相似度和该类故障组合在仿真集Ds中的占比,计算Ds和Dt的综合相似度:

(17)

3)仅使用试验集Dt训练一个普通SVM分类器作为基线(Baseline)。再向训练集中引入一定数目的仿真集样本,多次改变仿真集样本的分布占比、数据量以及具体样本,直到式(15)中的NTG=0,此时仿真集与试验集的综合相似度即为最低迁移阈值St。

4)迁移学习试验开始前,需对所选仿真集进行相似度检验,若计算出的综合相似度Sω≤St,则需重新选择样本。若Sω>St,则将2.3节步骤2中的初始权重向量进行初始化后开始学习训练,初始权重为

(18)

这一步的目的是基于综合相似度进一步缩小仿真集样本的初始权重,以加快收敛,在规定的迭代次数内获得更多符合性能要求的基分类器。

综合特征向量提取,迁移学习策略,负迁移度考察后,供药装置故障诊断的完整方法流程如图7所示。

3 故障诊断试验与分析

3.1 试验条件

本文所用的供药装置试验样本来自于专用的供药装置台架,针对典型故障问题采集了各类选药数-故障类型组合的样本。

图7 供药装置故障诊断方法流程图Fig.7 Flowchart of fault diagnosis method for modular charge feeding mechanism

图8 供药装置台架实物图Fig.8 Bench of modular charge feeding mechanism

该台架数据采集系统通过安装在链轮处的光电编码器采集(16位,编码器采样频率为1 kHz),采集到离散信号后通过控制器域网(CAN)反馈给可编程控制器(PLC, 贝加莱PLC- X20 IF 1072),PLC再通过以太网线再将样本信号传输给上位机分析并保存。整体结构如图8所示,储药仓变形局部细节如图9所示,阻尼块失效局部细节如图10所示。

图9 储药仓变形局部细节Fig.9 Details of cartridge deformation

图10 阻尼块磨损局部细节Fig.10 Details of damping block wear

3.2 可迁移度试验

根据式(17),综合相似度与仿真集和试验集样本的平均相似度以及仿真集样本的分布有关。

先在台架试验样本中利用自助采样法抽取样本,提取特征向量后组成用于训练的试验集,由于实际试验样本中包含各类故障的样本占比很少且不平衡,所以采用自助采样法扩充含故障样本时,含故障样本和健康样本不宜采用相同比例,防止同一故障样本被反复采样而造成训练过拟合。试验集各类选药数-故障类型组合的分布如表2所示。

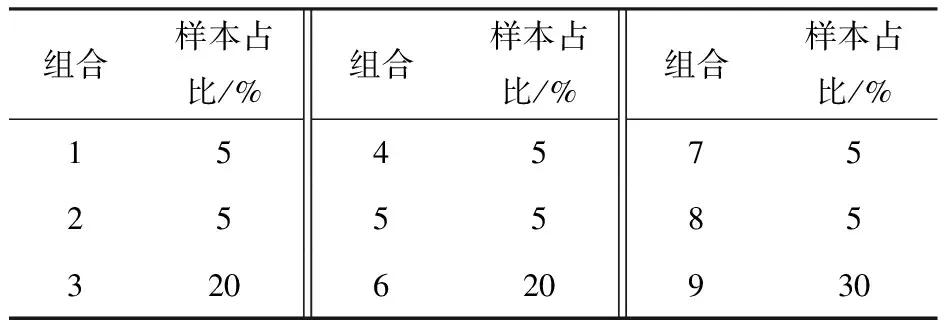
表2 试验集各类组合样本的占比Table 2 Distribution of various combinations in the bench test set

在仿真样本中利用随机采样法抽取样本,提取特征向量后组成用于辅助训练的仿真集。本文采取两种仿真集样本分布策略:策略1为与试验集样本同分布;策略2为均匀分布(组合9占比稍多)。具体如表3和表4所示。

表3 仿真集各类组合样本的占比(策略1)Table 3 Distribution of various combinations in the simulation set (Strategy 1)

表4 仿真集各类组合样本的占比(策略2)Table 4 Distribution of various combinations in the simulation set (Strategy 2)

设置一个传统的SVM分类器应用于本文研究对象作为对比基线,超参数如下:

按表2要求分布的试验集样本合计500组;SVM核函数为高斯核函数;迭代次数为20次;寻优方法为粒子群优化算法;验证方法为K折验证法,K=5。样本构造的自相关汉克尔矩阵的维数定为Q=200,特征向量维数定为50。

该基线在测试集得到的错误率ε=19.67%。

设置寻找迁移阈值的迁移学习参数如下:

按表2要求分布的试验集样本合计500组;选取仿真集样本若干组,仿真集的样本占比分布需符合表3策略1或表4策略2,仿真集的样本数目需为500组、1 000组或2 500组。设置迭代次数Ite=20,多次选取符合不同要求组合的仿真集,计算该次的综合迁移度Sω后执行迁移学习任务。统计结果如表5、表6所示。与基线的错误率进行比较,可得到最低迁移阈值St≈0.7。

表5 仿真样本按策略1分布时的迁移阈值Table 5 Transfer threshold of Strategy 1

表6 仿真样本按策略2分布时的最低迁移阈值Table 6 Transfer threshold of Strategy 2

由表5和表6可以看出,提升综合相似度和扩大仿真集样本量对分类准确率的提升均有正面效果。用于迁移学习的仿真集数据较少时,提升分类性能需要与试验集样本有更大的相似度,而仿真集数据较多时,达到相同的测试准确率可以有更宽松的迁移阈值,更有助于迁移阈值的选取。仿真集样本按策略2分布迁移阈值整体更小,说明引入更多故障仿真样本更有利于提升整体的分类准确率。

3.3 迁移学习试验与性能分析

根据3.2节结论,进行基于迁移学习的供药装置故障诊断方法的性能试验:

设定迭代次数Ite=20,以自助采样法选取500组试验样本提取特征组成试验集Dt,按表4策略2分布随机抽取2 500组仿真样本提取特征组成仿真集Ds,预留300组从未参与训练的台架试验样本提取特征作为测试集。对其中一次综合相似度Sω=0.9的训练集产生的分类器进行性能分析。3.2节中作为基线的传统SVM分类器,该次训练中首轮迭代的基分类器以及迭代完成后的集成分类器的分类混淆矩阵如图11所示。对比图11中的3个分类混淆矩阵可以看出,本文方法对供药装置的故障诊断问题具有较好的效果,传统SVM分类器综合准确率为80.7%,首轮迭代的基分类器综合准确率为78.7%,集成分类器相较前二者性能提升明显,综合准确率达到了96.3%。

图11 3个分类器的混淆矩阵Fig.11 Confusion matrices of the three classifiers

针对输药块数分类和故障类型分类的效果分别考核,传统SVM分类器、基分类器和集成分类器的分类准确率和F1值见表7和表8,图12为3个分类器分类准确率的横向比较。从表7和表8中可以统计出:本文方法针对模块药数量的分类准确率达到了99.7%,针对故障类型的分类准确率也达到了96.3%。图12显示传统SVM分类器和基分类器性能相近,且它们对输药块数分类时性能要略优于对故障状态的分类,这是因为不同模块药数量的样本在训练集中分布平均且数量充足。针对故障类型的分类问题,受限于含故障试验样本数量和分布,需借助迁移学习方法多次迭代后获得集成分类器提升准确率。

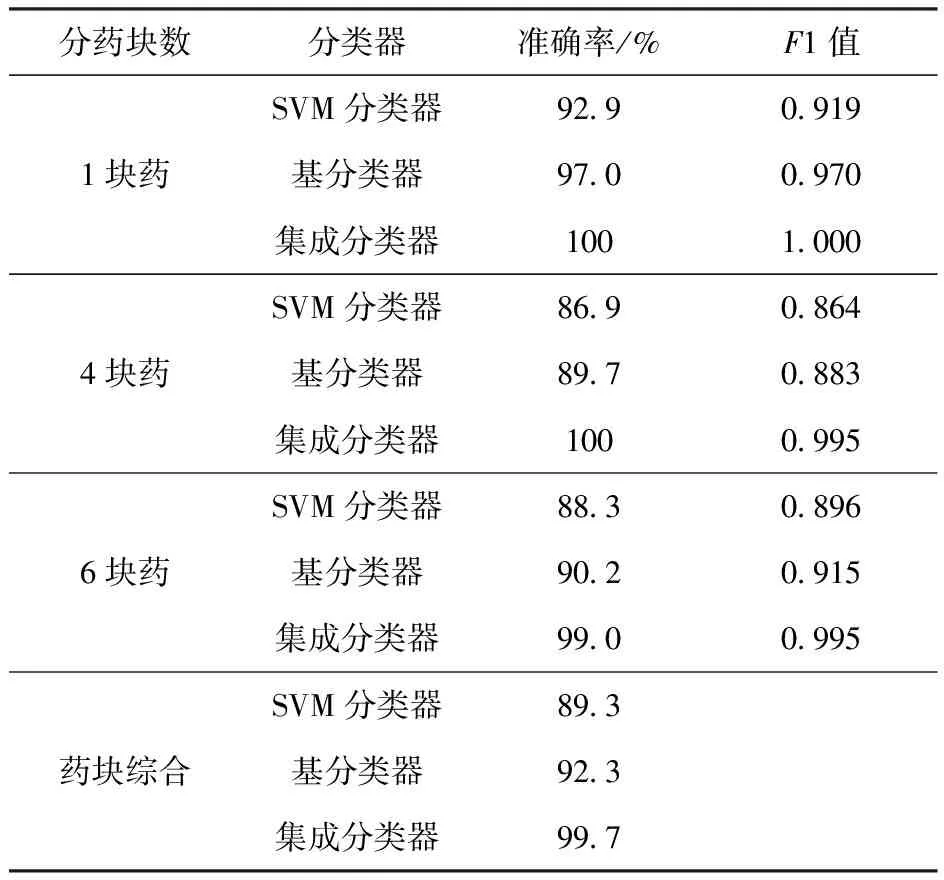
表7 分药数目分类的准确率和F1值Table 7 Accuracy and F1 value statistics for modular charge numbers

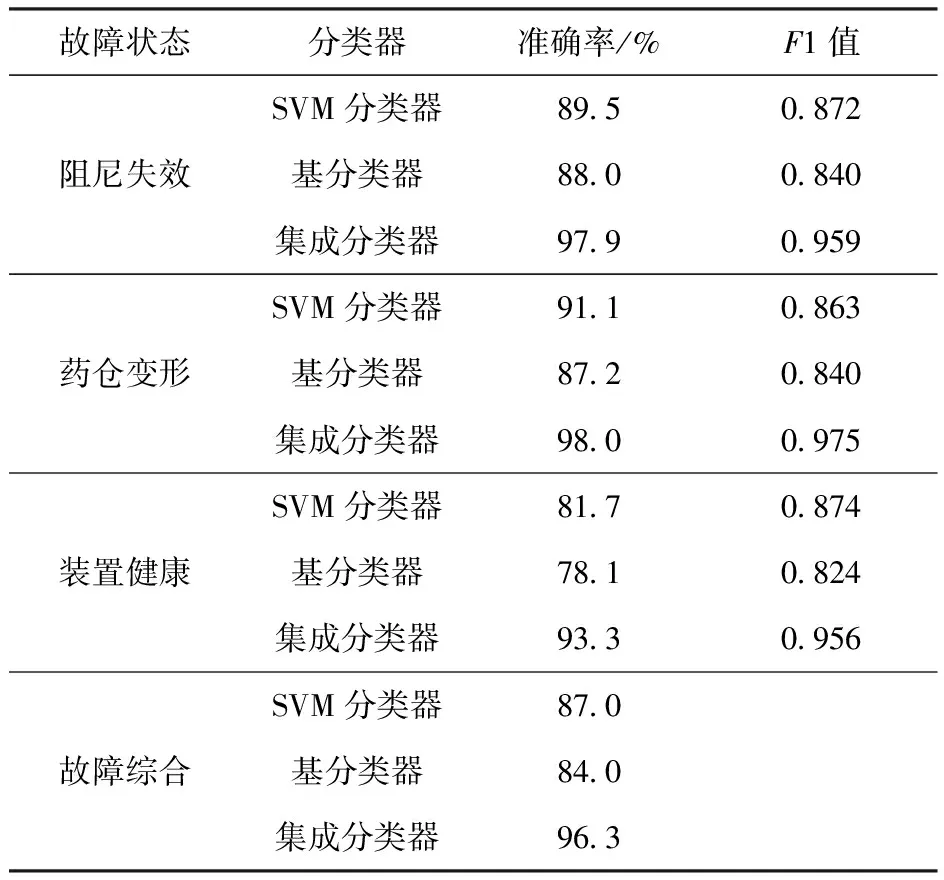
表8 故障类型分类的准确率和F1值Table 8 Accuracy and F1 value statistics for fault classification

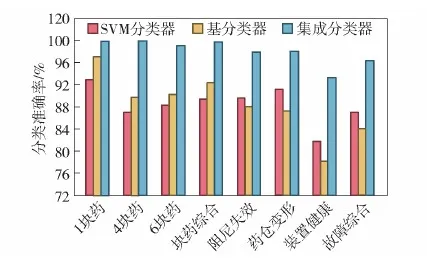
图12 3个分类器的单项分类准确率Fig.12 Accuracy of single classification from the three classifiers

4 结论

本文结合自相关矩阵-SVD的特征提取法与迁移学习策略提出一种适用于供药装置的故障诊断方法,使用计算机仿真方法生成与供药试验样本近似的仿真数据,对两类数据进行特征提取后联合训练一个WSVM,在TrAdaBoost算法框架下对所有样本的权重进行迭代更新,最终得到一个可以适用于供药装置故障诊断的集成分类器。得到以下主要结论:

1)自相关矩阵-SVD方法能够有效提取故障微弱信号特征,能同时满足对供药过程原始数据的降噪和降维需求,以此法提取的故障特征可以适应本文方法,获得了较好的分类效果和分类效率。

2)作为辅助训练的供药仿真数据只需与供药试验数据具有一定的相似度就能对训练产生积极作用,在建立仿真模型时可以相对简化。与传统故障诊断方法相比,也不需要通过花费高昂成本获取大量试验数据来提升准确率。

3)针对供药装置故障样本稀缺且分布不平衡情况下的故障诊断问题,本文所采用的方法相较传统机器学习方法有明显优势,综合诊断准确率可以达到96.3%,将之应用到工程实践中,对供药装置正确完成分药任务是一种可靠保障。