“线性规划”复习的“三把钥匙”

■四川省绵阳外国语学校 李学军

从近几年的高考试卷来看,线性规划考点的试题多出现在选择题和填空题中。考查方向主要集中在三个方面:一是求目标函数的最值;二是根据目标函数的最值求参数的取值范围;三是运用“线性规划”思想解决综合性问题。考查方向的三类问题的一般解法就是“线性规划”问题的“三把钥匙”。以下举例说明在高考复习备考中如何获取这“三把钥匙”。

一、掌握求目标函数最值的基本方法,取得“入门钥匙”

1.求线性目标函数的最值

例1若实数x,y满足约束条件求z=2x+y的取值范围。

解析：根据约束条件作出可行域,如图1所示。

图1

目标函数的特征直线l与AC:2x+y-4=0 平行,易得点A(2,0),联立可得点B(6,2)。平移直线l经过点A时,z取最小值,zmin=2×2+0=4;平移直线l经过点B时,z取最大值,zmax=2×6+2=14。所以z的取值范围为[4,14]。

归纳：求线性目标函数最值的一般步骤:①正确作图表示可行域,注意边界的虚实;②将目标函数变形为斜截式y=-2x+z;③找到目标函数的特征直线;④在目标函数的斜截式方程中,分析纵截距最大或最小时与目标函数取最大或最小值的对应关系,从而确定要计算的最优解;⑤计算最优解,并代入目标函数求出目标函数的最值。

变式1已知实数x,y满足约束条件

(1)求使目标函数z=3x+y取最小值的最优解对应的点(x,y)。

(2)求使目标函数z=x+y取最小值的最优解对应的点(x,y)。

分析：(1)如图2,目标函数z=3x+y化为y=-3x+z,其特征直线y=-3x的倾斜角小于可行域的边界直线AC的倾斜角,故使z=3x+y取最小值的最优解对应的点为C(1,2)。

图2

(2)如图3,目标函数z=x+y化为y=-x+z,其特征直线y=-x的倾斜角大于可行域的边界直线AC的倾斜角,故使z=x+y取最小值的最优解对应的点为A(2,0)。

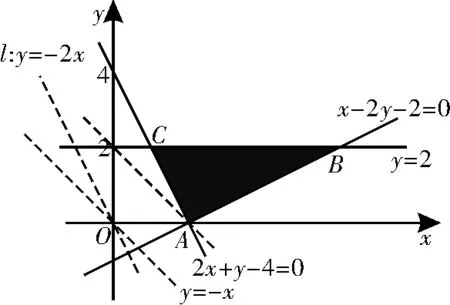
图3

归纳：①特征直线与边界直线的倾斜角的大小关系,直接影响最优解的位置;②目标函数的最优解有可能不止一个。

变式2若实数x,y满足约束条件求x-2y的取值范围。

分析：根据约束条件作出可行域,如图4所示。令z=x-2y,则,易得点A(2,0),联立可得点C(1,2)。平移直线l:经过点A时,z取最大值,zmax=2-2×0=2;平移直线l经过点C时,z取最小值,zmin=1-2×2=-3。

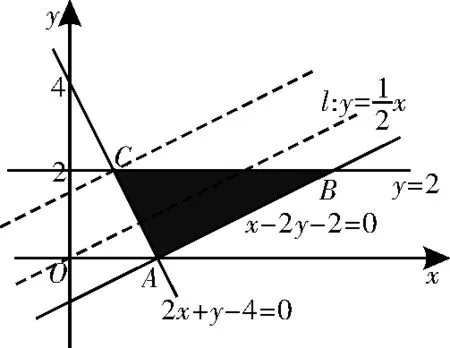
图4

所以x-2y的取值范围为[-3,2]。

归纳：目标函数的最值要与截距的最值正确对应,避免在最优解的选择上出现错误。

2.求非线性目标函数的最值

例2若实数x,y满足约束条件的取值范围。

解析：根据约束条件作出可行域,如图5 所示。表示可行域内的点与定点D(6,1)连线的斜率,易得边界直线AD的斜率=,根据倾斜角的变化范围可知的取值范围为。

图5

归纳：求非线性目标函数最值的一般步骤:①正确作图表示可行域,注意边界的虚实;②把目标函数抽象成可行域内的点满足的几何(如斜率、距离等)要素;③根据几何要素进行动态分析,找到满足条件的可行解的边界;④根据可行解区域范围及边界的几何要素的取值,写出目标函数的最值。

变式1若实数x,y满足约束条件的取值范围。

分析：根据约束条件作出可行域,如图6所示。表示可行域内的点与定点E(3,4)连线的斜率,计算边界直线的斜率得kCE=1,,受倾斜角范围的影响,斜率(即目标函数值)的范围不连续,故的取值范围为。

图6

变式2若实数x,y满足约束条件求|3x+4y-3|的取值范围。

分析：根据约束条件作出可行域,如图7所示。|3x+4y-3|可化为,其几何意义是可行域内的点到定直线3x+4y-3=0 的距离的5 倍,其最小值为=3,最大值为=23,故|3x+4y-3|的取值范围为[3,23]。

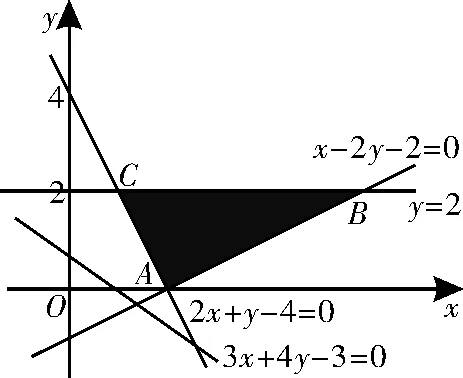
图7

归纳：①抽象为斜率的非线性目标函数,应根据倾斜角可行的变化范围对应出斜率的取值范围,该范围不一定是一个连续区间。②个别非线性目标函数在进行变形(配方、分离常数、配凑)后,可以抽象出斜率、距离等几何要素,故也可以用线性规划思想求其值域。

二、学会根据目标函数最值求参数的值,获得“进阶钥匙”

1.参数出现在约束条件中

例3已知实数x,y满足约束条件其中a∈R,若点(x,y)构成的图形面积为6,则实数a的值为_____。

解析：如图8所示,直线2x+ay-4=0经过定点A(2,0),由题意知△ABC的面积为6,即|BC|=6,由故点B(6,2),于是点C的坐标为(0,2),把C(0,2)代入2x+ay-4=0,解得a=2。

图8

归纳：约束条件中含有参数的分析思路:①分析含有参数的边界直线所过的定点,及参数对此边界直线位置的影响;②分析题目中与参数有关的数量关系,确定求解参数的方法。

2.参数出现在目标函数中

归纳：目标函数中含有参数的分析思路:①将目标函数化为斜截式,分析参数对目标函数的位置及最优解的影响;②根据目标函数取值的特征,建立参数的数量关系求参数的值。

三、掌握“线性规划”综合性问题的分析方法,获得“通关钥匙”

例5设f(x)是定义在R 上的增函数,对任意的x都有f(1-x)+f(1+x)=0恒成立,若实数m,n满足不等式组则m2+n2的取值范围为_____。

解析：由f(1-x)+f(1+x)=0 得f(1-x)=-f(1+x)。

由f(m2-6m+23)+f(n2-8n)＜0得f(m2-6m+23)＜-f[1+(n2-8n-1)]。

所以f(m2-6m+23)＜f[1-(n2-8n-1)]=f(2-n2+8n)。

因为f(x)是R上的增函数,所以m2-6m+23＜2-n2+8n,即(m-3)2+(n-4)2＜4,所以已知约束条件可转化为

可行域是以(3,4)为圆心,2为半径的圆的右半部分(不含圆周和直径),如图10 所示,目标函数m2+n2表示原点到可行域内的点的距离的平方。

图10

所以(m2+n2)min=|OA|2=32+22=13;(m2+n2)max=|OB|2=。

由于不含圆周和直径,故m2+n2的取值范围为(13,49)。

归纳：①注意挖掘题目中隐含的约束条件(二元一次不等式组);②灵活应用线性和非线性目标函数最值的求法,解决实际问题。

变式若函数f(x)=x2+1 的定义域为[a,b],值域为[1,5],则在平面直角坐标系内,点(a,b)与两坐标轴围成的图形的面积为_____。

分析：由函数f(x)=x2+1的图像(图略)知a,b需满足所以点(a,b)与两坐标轴围成的图形是边长为2的正方形,故面积为4。